超声换能器的“电感-变压器”阻抗匹配模型研究

韩旭，章康宁，郑海祥，马青玉



超声换能器的“电感-变压器”阻抗匹配模型研究

韩旭1，章康宁2，郑海祥1，马青玉1

(1. 南京师范大学物理科学与技术学院，江苏南京 210023；2. 南京邮电大学通信与信息工程学院，江苏南京210023)

在分析超声换能器阻抗特性和电路匹配的基础上，对传统纯电感电容匹配电路模型进行电路仿真和阻抗分析，证明该模型在谐振频率附近有大范围的电抗变化，存在电路不稳定和电阻调节精度低的问题；提出“电感-变压器”阻抗匹配模型，通过电感和变压器分别调节换能器电阻和电抗，实现电路的精确匹配，以提高超声换能器阻抗匹配的精度和稳定性，并给出了理想的匹配条件和匹配参数。利用匝数可调的变压器和电感制作了超声换能器的匹配电路，对20.8 kHz的变幅杆换能器进行了阻抗匹配的实验测量，结果证明这种“电感-变压器”阻抗匹配模型在谐振频率附近具有较小的电抗变化范围、较低的电阻变化率和较高的电抗调节精度，在超声换能器的自动阻抗匹配中具有良好的应用前景。

超声换能器；阻抗匹配；“电感-变压器”匹配模型；高精度调节

0 引言

超声技术在近年来得到高速发展，其应用已经渗透到生活的各个领域，如航天航空、建筑、无损检测、医学成像、超声治疗等[1]。在超声的研究和应用中，超声换能器是一种能量转换器件，在谐振频率附近等效成电阻和电容串联[2]，只有当换能器和超声电源阻抗匹配时，输出的超声能量最大，电路的能量输出效率最高；反之，如果超声电源和负载失谐则会降低其能量激发的效果，严重时甚至会损坏超声电源[3,4]。当前对于换能器阻抗匹配的研究大多采用的是电感电容匹配电路模型[5-13]，或用固定匝数比的变压器来匹配[14-16]，国内外学者经过大量的研究，提出了T型匹配网络[7]和耦合振荡匹配模型[8]来提高能量的传输效率，构建了电感加电容的阻抗动态匹配网络[9]，取得了较好的匹配效果。但是电感加电容匹配模型的电路存在匹配范围小和调节精度低的问题，虽然通过增加电感和电容可使电路达到较好的匹配状态，而电感和电容的增加相应产生了电路的极值点，给电路稳定性带来隐患，同时增大了电路调试的难度，不利于换能器阻抗的自动匹配设计。近年来，有研究报道利用变压器可以实现阻抗匹配[13-15]，但目前的研究大都使用固定匝数比的变压器匹配电路，适合特定的负载电路，其可调整性较差，并没有对电路适用条件、阻抗调整精度和能量传输效率进行细致的理论研究和实验测量。

本文研究构建了新型“电感-变压器”阻抗匹配模型，改变可调变压器初级线圈的匝数来调节匹配电路的等效电阻，调节电感线圈的匝数来匹配电路的电抗，实现理想匹配。仿真和实验结果证明，在匝数调节过程中匹配电路电阻和电抗平缓增加，不发生阻抗突变，这种“电感-变压器”匹配电路调节方便，工作稳定，适合进行计算机控制下的自适应匹配，在超声换能器的自动匹配中具有良好的应用前景。

1 阻抗匹配模型分析

1.1 纯电感电容阻抗匹配模型

对于采用纯电感电容匹配模型的超声换能器，其在谐振频率附近等效电路可以简化成如图1所示的电路模型，其中为超声换能器在谐振频率下的阻抗，由等效电容和等效电阻串联组成，为匹配电容，为匹配电感。

在理想匹配时，超声电源两端的匹配电路必须等效为纯电阻，且其大小等于超声电源的内阻[4]，等效电路可以表示为

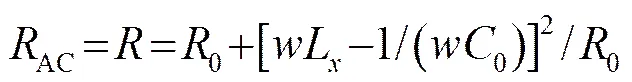
(2)

(3)

1.2“电感-变压器”阻抗匹配模型

为了克服纯电感电容匹配中的不足，提高电路匹配的灵活性和可调性，本研究结合电感和变压器匹配，提出了一种电路结构简单、调节控制方便、阻抗匹配精度高、能量传输效率高的“电感-变压器”阻抗匹配模型。

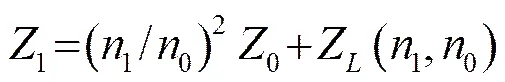
(5)

(7)

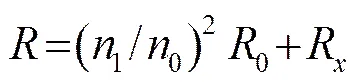
(9)

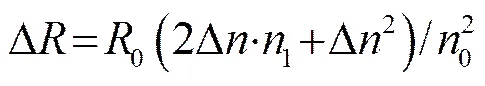
(11)

“升压变压器-电感”阻抗匹配模型的电路结构如图3所示，匹配模型先通过变压器调节进行电阻匹配，后通过电感调节实现电抗匹配。电路中超声电源两端(变压器初级线圈)的阻抗为

为了达到理想匹配，电路模型必须满足：

(13)

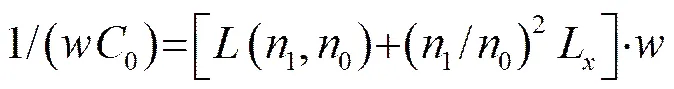
(15)

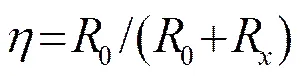
1.2.3 两种“电感-变压器”匹配模型的特性比较

实际测量中可调电感有一定的电阻值，若换能器的负载电阻比较小，通过式(11)、(16)可以得出，匹配模型比匹配模型传输效率低,而负载电阻较大时，匹配模型比匹配模型的能量传输效率高。因此为了提高整个匹配电路能量传输效率，对于换能器阻抗>电源内阻(负载阻抗较高)的匹配电路和电源内阻>换能器阻抗(负载阻抗比较低)的匹配电路，分别采用“升压变压器-电感”和“电感-降压变压器”的匹配电路。

在纯电感电容的匹配电路中，电抗值会在电感匝数调节时发生突变。如果在阻抗匹配中不增加其它抗性元件，对所加的负载有一定的限制；如果增加抗性元件，电路可以实现理想匹配，但增加抗性元件的同时也增加了阻抗突变的极点，给电路调节带来不便。对于变压器加电感匹配电路，可调电感主要改变匹配电路的电抗值，变压器匝数可以调节匹配电路的等效电阻值，电抗和电阻可以分别精确调整。

2 阻抗匹配模型的仿真分析

仿真所用换能器的谐振频率设定为20.8 kHz，通过串联C-R模型测量其在谐振频率附近的谐振电阻为=14 Ω，等效电容为=23 nF，匹配模型的电感线圈参数设为：=0.48，=1，=5，=100 mm，=0.8983*10-3m2，电感匝数为=200。

2.1 纯电感电容阻抗匹配模型

在匹配电感线圈匝数的调节中，匹配的电阻值变化非常大。在调节电感线圈匝数，使电阻值从最大值下降到最小值的过程中，电阻值的平均变化率约为60 Ω/匝；在=126匝时，其电阻接近50 Ω，在126匝附近小范围匝数调节的电阻变化率约为8 Ω/匝；可见匹配电路的电阻匹配调节的精度较低，很难实现阻抗的高精度匹配。同时在=126匝时，匹配电路的电抗变化较快，在电感匝数调节时会产生电抗的突变，因此匹配电路容易受到外界干扰，导致电路失配，在实际应用中难以实现电路的自动匹配。

2.2 “电感-变压器”阻抗匹配模型

3 实验测量

实验测量中，选用谐振频率为20.8 kHz的压电陶瓷变幅杆功率超声换能器进行阻抗匹配和测量，可调变压器用直径为0.45 mm的漆包线在EE85B型锰锌铁氧化体磁芯上绕制而成，可调电感采用直径为0.45 mm的漆包线在长为140 mm、直径为10 mm的圆柱形锰锌铁氧化铁磁棒上绕制而成。用Agilent 4294A精密阻抗分析仪进行阻抗测量时首先进行校准，选择模型。设置扫描频率的中心频率为20.8 kHz，带宽为2 kHz，采用801采样点数的线型扫描，然后对双极夹具进行开路和短路补偿，最后激活通道A和通道B进行测试。

3.1 超声换能器的阻抗测量

经阻抗分析仪测量得到超声换能器在20~22 kHz的阻抗特性如图6所示，可见变幅杆超声换能器的最小阻抗在20.95 kHz处，而在标称谐振频率20.8 kHz下阻抗幅值为87.81 Ω，幅角为-83.30°，换能器呈现容性，用C-R串联等效电路计算得到其电容=87.2 nF，电阻=10.31 Ω。由于换能器电阻小于功率放大器(E&I 2200L)的标准输出电阻50 Ω，故选择“电感-降压变压器”的匹配模型。

3.2 变压器匹配模型的阻抗测量

根据测量的换能器谐振频率和电阻，设计变压器初级线圈为110匝(可调)，次级线圈50匝(固定)，通过改变接入电路变压器初级线圈匝数来调节换能器的等效阻抗。实验测量得到变压器的初级线圈匝数和等效电抗的关系如图7所示，可见随着变压器初级线圈匝数的增加，匹配电路的等效电阻呈上升趋势，而电容呈下降趋势。当初级线圈从10匝增加到110匝时，其等效电阻从1.324 Ω增加到52.67 Ω，而电容从3.171 μF递减到24 nF。经计算得到初级线圈每增加一匝，匹配电路等效电阻的最大变化率为0.9 Ω/匝，其阻抗调节精度为98.2%。

3.3 “电感-变压器”匹配模型的阻抗测量

通过步进电机丝杆控制可以调节电感和变压器的线圈匝数，实现“电感-变压器”模型的匹配，并测量得到变幅杆换能器在理想匹配条件下的阻抗特性如图8所示，可见经阻抗匹配后换能器在谐振频率为20.8 kHz时阻抗最小，此时整个匹配电路阻抗为49.6 Ω，幅角为-0.98°。进一步测量可调电感两端的电阻为1.5 Ω，得到匹配电路的能量传输效率可以达到96.97%。

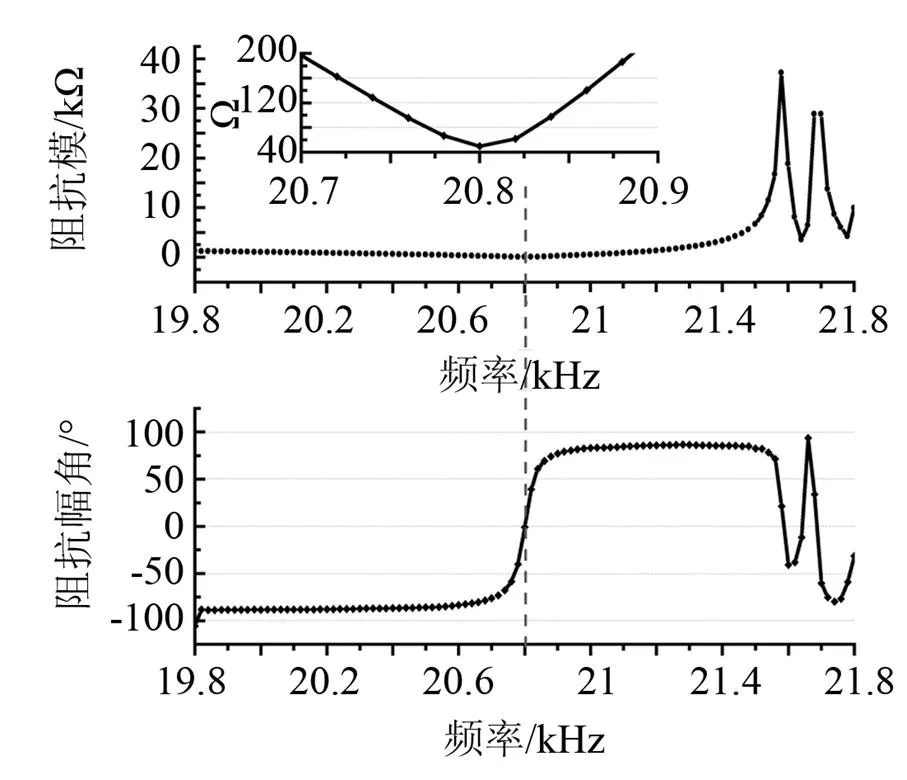
图8 “电感-变压器”匹配模型的等效阻抗特性图

4 总结

本文先从理论上分析了传统纯电阻和电容匹配方法的不足，存在匹配范围受限和匹配精度不高的缺点。为了达到理想匹配，电路需增加大量抗性元件，这样给匹配模型增加大量极点，给电路稳定性带来隐患。为了克服传统匹配模型的这些缺点，提出了一种“电感-变压器”阻抗匹配模型，通过电感调节换能器的电抗，通过变压器调节电路的电阻，实现电路的精确匹配，减少了极点，有效提高了超声换能器匹配的稳定性和调节精度，增加能量传输的效率；接着通过理论计算和仿真得出模型的理想匹配条件和匹配参数。最后利用步进电机控制电感线圈和变压器匝数，建立了阻抗匹配实验电路，测试结果证明“电感-变压器”阻抗匹配模型具有良好阻抗匹配特性和96%以上的能量传输效率，可以实现计算机控制下的自动匹配，具有良好的线圈调节和阻抗匹配精度，在超声换能器的自适应匹配中有着良好的应用前景。

[1] 林仲茂. 20世纪功率超声在国内外的发展[J]. 声学技术, 2000, 19(2): 101-105.

LIN Zhongmao. Development of high power ultrasonics in China and abroad during 20 century[J]. Technical Acoustics, 2000, 19(2): 101-105.

[2] 王艳东. 压电换能器在并联谐振频率附近的特性及自动频率跟踪的研究[D]. 西安: 陕西师范大学, 2006.

WANG Yandong. Study on the behavior of the piezoelectric transducer around its parallel resonant frequency and automatic frequency tracing[D]. Xi’an: Shaanxi Normal University, 2006.

[3] 胡长阳. D类和E类开关模式功率放大器丛书[M]. 北京: 高等教育出版社, 1985.

HU Changyang. Class D and Class E Series switch mode power amplifier[M]. Beijing: Higher Education Press, 1985.

[4] Agarwal A, Lang J. Foundations of analog and digital electronic circuits[M]. Morgan Kaufmann, 2005.

[5] 鲍善惠, 王艳东. 压电换能器在并联谐振频率附近特性的研究[J]. 声学技术, 2006, 25(2): 165-168.

BAO Shanhui, WANG Yandong. Behavior of piezoelectric transducer at frequencies near parallel resonance[J]. Technical Acoustics, 2006, 25(2): 165-168.

[6] 方由艳, 林书玉. L 型匹配网络对超声换能器振动性能的影响[J]. 声学技术, 2010, 29(1): 112-115.

FANG Youyan, LIN Shuyu. Effects of L-type matching network on characteristics of ultrasonic transducers[J]. Technical Acoustics, 2010, 29(1): 112-115.

[7] 韩庆帮, 林书玉, 鲍善惠, 等. 超声换能器电匹配特性研究[J]. 陕西师范大学学报: 自然科学版, 1996, 24(4): 114-115.

HAN Qingbang, LIN Shuyu, Bao Shanhui, et al. Characteristics of matching circuit of ultrasonic transducers[J]. Journal of Shaanxi Normal University: Natural Science Edition, 1996, 24(4): 114-115.

[8] 鲍善惠. 压电换能器的动态匹配[J]. 应用声学, 1998, 17(2): 16-20.

BAO Shanhui. Dynamic matching for a piezoelectric transducer[J]. Applied Acoustics, 1998, 17(2): 16-20.

[9] 孔权. 压电换能器自动阻抗匹配系统的设计[D]. 重庆: 重庆医科大学, 2011.

KONG Quan. The design of automatic impedance matching system for ultrasound[D]. ChongQing: ChongQing Medical University, 2011.

[10] 林书玉, 张福成. 压电超声换能器的电端匹配电路及其分析[J]. 压电与声光, 1992, 14(4): 29-38.

LIN Shuyu, ZHANG Fucheng. Analyses of matching circuits of piezoelectric ultrasonic transducers[J]. Piezoelectrics and Acoustooptics, 1992, 14(4): 29-38.

[11] 陈航, 滕舵, 钱惠林. 宽频带换能器电匹配网络设计方法[J]. 声学技术, 2008, 26(5): 954-957.

CHEN Hang, TENG Duo, QIAN Hui-lin. Technology research on electricity matching for broadband transducer[J]. Technical Acoustics, 2008, 26(5): 954-957.

[12] 吴运发. 水声宽带换能器匹配技术研究[J]. 声学技术, 2000, 19(2): 87-89.

WU Yunfa. Technology research on match of wide band underwater acoustic transducer[J]. Technical Acoustics, 2000, 19(2): 87-89.

[13] Huang H, Paramo D. Broadband electrical impedance matching for piezoelectric ultrasound transducers[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2011, 58(12): 2699-2707.

[14] Ashraf M, Aslam M. Impedance matching for underwater piezoelectric transducers using piezoelectric transformer[C]// Applied Sciences and Technology(IBCAST), 2013 10th International Bhurban Conference on IEEE, 2013: 308-311.

[15] 蒋锟林. 压电换能器匹配电路的设计[J]. 电声技术, 2012, 36(9): 26-29.

JIANG Kunlin. Design of Piezoelectric Transducer Matching circuit[J]. Audio Engineering, 2012, 36(9): 26-29.

[16] Lotfi A W, Wilkowski M A. Issues and advances in high-frequency magnetics for switching power supplies[J]. Proceedings of the IEEE, 2001, 89(6): 833-845.

Research on ‘transformer-inductance’ impedance matching model for ultrasonic transducer

HAN Xu1, ZHANG Kang-ning2, ZHENG Hai-xiang1, MA Qing-yu1

(1. School of Physics and Technology, Nanjing Normal University, Nanjing 210023, Jiangsu, China;2.School of Telecommunication and Information Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210023, Jiangsu, China)

Based on the analyses of impedance characteristics and matching circuit of ultrasound transducer, it is found that with the traditional inductance capacitance matching circuit, a wide range of reactance variation around the resonant frequency appears and causes the circuit stability and regulatory accuracy reduced. Therefore, a ‘transformer-inductance’ matching model is proposed in this paper. The reactance and resistance can be regulated by the adjustable inductance and transformer to improve the precision and stability of the matching circuit for ultrasonic transducer, and the ideal matching condition and parameter are provided. In experiments, with the controllable transformer and inductance, a matching circuit is developed for an ultrasonic horn transducer with the center frequency of 20.8 kHz. It is proved that the matching circuit has a narrow impedance variation range with high reactance regulatory accuracy when the frequency is close to the resonance, which provides application potential in automatic impedance matching of ultrasonic transducer.

ultrasonic transducer; impedance matching;‘transformer-inductance’ model; precise adjustment

TB552

A

1000-3630(2015)-04-0380-05

10.16300/j.cnki.1000-3630.2015.04.017

2014-09-22;

2014-12-15

国家自然科学基金项目(11274176和11474166)、江苏高校优势学科建设工程资助项目

韩旭(1989－), 男, 安徽黄山人, 硕士研究生, 研究方向为电子信息和超声应用系统设计。

马青玉, E-mail: maqingyu@njnu.edu.cn