一种板壳式换热器壳程物流分配特性的模拟与优化
刘家瑞,赵 巍,黄晓东,张 华
(1上海理工大学能源与动力工程学院,上海 200093;2东莞埃欧热能技术有限公司,广东 东莞 523053)
一种板壳式换热器壳程物流分配特性的模拟与优化
刘家瑞1,赵巍1,黄晓东2,张华1
(1上海理工大学能源与动力工程学院,上海 200093;2东莞埃欧热能技术有限公司,广东 东莞 523053)
以一种板壳式换热器壳程为研究对象,建立了几何模型并进行了数值模拟,通过对各流道的流量偏差和相对标准差的计算,分析了壳程物流分配的特性,并总结了物流分配特性对换热器的传热效率、整体效能以及压降的影响。模拟与分析结果显示:换热器壳程存在严重的物流分配不均匀现象,这种现象会造成换热器整体效能的下降,同时造成压降的大幅升高,但是对于传热效率的影响很小,总换热量偏移不足3%。为了改善物流分配带来的影响,提高换热器的性能,通过在入口处设置封头和圆弧状条纹板对换热器壳程来进行优化设计。优化分析结果表明:该设计可以改善换热器物流分配不均匀性,并能使换热器效能下降明显降低,压降相对减小,可以为板壳式换热器的优化提供参考。
板壳式换热器;物流分配;传热;数值模拟;优化设计
板壳式换热器属于紧凑式换热器,这类换热器通常会出现内部物流不均匀以及温度场分布不均的情况,因而会影响换热器的整体效能。物流分配的不均匀会加剧温度场分布的不均匀,所以是影响换热器效能的主要因素,相关研究表明物流分配的不均匀性可使换热器整体效能降低30%以上。
Fleeting[1]建立了换热器内部分配不均匀性模型,研究了不同传热单元数下物流分配不均匀性对换热器效能的影响,研究表明随着传热单元数的增加。物流分配不均匀性对换热器效能的影响逐渐增大;焦安军等[2-4]建立了连续性模型和离散模型,前者能有效计算物流分配不均匀导致能效下降的比率,后者则为控制实验研究的精度提供了理论依据。赵镇南[5-6]对物流分均匀布置导致板式换热器传热性能下降作了计算和分析,发现当冷热流体进出口位于换热器同侧时,各流道传热量明显不同但总传热量变化不大,而进出口位于两侧时,总传热量比按均匀分布计算时低20%。邓先和等[7]通过建立换热器壳程数学模型来研究流速分布不均造成传热负荷的偏移,结果表明流速的不均匀分布对换热器传热性能的影响很小,传热负荷偏移在1%以内。
在设计换热器时,一般通过增加富余量来弥补由于物流分配不均而导致的换热器效能下降,但是这样做的后果是所需换热面积增加20%~40%,这不仅造成成本增加,而且容易造成资源浪费,为了改善这种情况,对换热器进行优化设计十分必要。
焦安军等[2-4]提出了在板翅式换热器导流片内部增设补液腔的思想,研究了不同的导流片角度、导流片结构参数h/H对于单相流动分配的影响,还提出了在入口处设置二次封头的概念,研究发现当量直径比为1时,物流分配较为均匀。文键等[8]提出在换热器基本封头中间添加不均匀打孔的孔板来改善流体分配的均匀性,结果表明合理设计与布置封头可以大大改善换热器入口物流分配特性。姚成林等[9]则提出导流翼,该导流翼上布置圆孔,圆孔面积从中间向两侧增大,底部出口处圆孔均匀排列,结果显示该结构能有效地改善物流分配特性。
本文针对板壳式换热器的壳程入口进行研究,利用数值模拟软件分析入口处物流分配特性,建立了壳程物流分配模型,根据模拟结果分析物流分配不均匀对于板壳式换热器效能的影响,并提出一种优化设计的方案,这对于板壳式换热器壳程物流特性的研究具有积极意义。
对于单相不可压缩流体,满足连续性方程、动量方程和能量方程[11]。
1 板壳式换热器壳程数值模拟
1.1几何模型
以若干并联流道组成的板壳式换热器壳程为研究对象。由于波纹流道结构较为复杂,对网格的要求较高易导致网格的数量巨大,并考虑到着重研究的是壳程入口物流分配的特性,不涉及板间流动特性与传热特性的研究,因而采用简化的平板替代波纹板构建几何模型[10]。几何模型如图1所示,主要尺寸如表1所示。

图1 壳程几何模型

表1 几何模型主要尺寸
利用CREO软件建立几何模型,几何模型包括6~11个流道的6个板壳式换热器壳程模型。通过ICEM软件对各几何模型进行网格划分,网格采用的是非结构化四面体网格。
1.2数学模型
数学模型基于以下假设:①流体为不可压缩的牛顿流体;②流体的流动为定常流动;③忽略浮升力的影响但考虑重力;④忽略流体的黏性耗散作用;⑤与空气接触的板片与周围环境绝热。
连续性方程见式(1)。
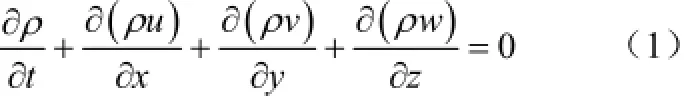
式中,ρ为流体密度,kg/m3;t为时间,s;u、v、w分别为控制体在x、y、z三个方向上的速度分量,m/s。动量方程见式(2)~式(4)。
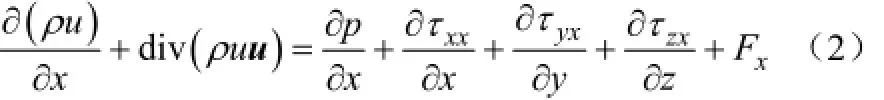
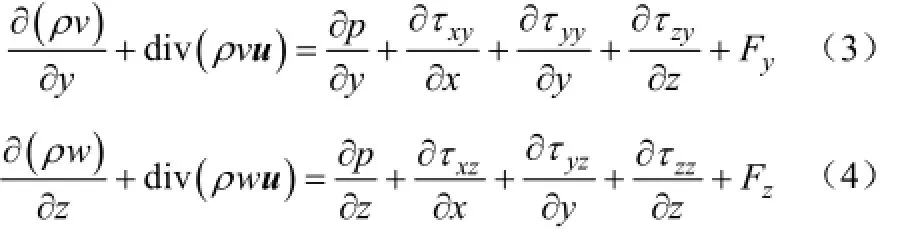
式中,p为控制体上的压力,Pa;u为速度矢量;xxτ、xyτ和xzτ等分别为作用在控制体表面上的黏性应力τ的分量,Pa·s;F为作用在控制体上的外力,N。
能量方程见式(5)。

式中,cp为流体比热容,J/(kg·K);T为温度,K;K为传热系数,W/(m2·K)。ST为由于黏性作用使流体机械能转换为热能的部分及流体的内热源。
本文采用的湍流模型为RNGk-ε模型,见式(6)、式(7)。

式中,iu为i方向上的速度分量;xi和xj是张量中的指标符号,i和j指标取值范围是(1,2,3);k为湍动能,m2/s2;ε为湍动能耗散率,m2/s3;μeff为有效黏度,kg/(m·s);kG为由于平均速度梯度引起的湍动能k的产生项;、2Cε为经验常数;Prk、 Prε为湍动能k和耗散率ε所对应的普朗特数;。
1.3边界条件
在设置边界条件时,流道的入口采用速度入口条件,出口则采用压力出口条件,外部边界设置为无滑移速度边界条件,流道的壁面设置为恒温壁面,壳程其余各面均设置为绝热壁面。此外采用分离式求解器隐式求解,压力与速度耦合采用SMPLE方法,离散化为二阶精度的迎风模式。
1.4模拟与分析
运用Fluent软件对各个流道换热器壳程进行数值模拟,图2为9流道换热器在雷诺数为2151时流速矢量图,图3为各流道入口速度分布云图。 从模拟的结果可以清晰看出,流体从入口管道流入流道时流体的速度分布是非常不均匀的,两侧区域流体流速明显低于距中心区域流体流速,大部分流体都集中在中心区域。主要原因在于,垂直流入通道时的流体首先要进入正下方流道,当流道截面不足以使所有流体通过时,产生较大阻力,导致横向压力梯度的产生,迫使流体向两侧扩散,扩散的流体在横向扩散的同时仍然要纵向流动,一方面流速会逐渐降低,另一方面两侧区域流道流入的流体相对较少,因此导致板壳式换热器壳程存在明显的物流分配不均匀现象。

图2 流速矢量图

图3 流道入口处流速分布云图
1.5物流分配特性分析
对于单相流动来说,量化物流分配均匀性的评价参数为流量偏差和相对标准方差,表达式为式(8)、式(9)[12]。

式中,Di为i流道的流量偏差;i为流道序号;S为相对标准差;qi为i流道的流量,kg/s;为平均流量,kg/s;n为流道数。
图4所示为9流道换热器对应的各流道流量,该图明显反映出不同流道间流体流量是不同的,随着雷诺数的增大,换热器各流道内最大流量与最小流量间差距明显增大,流量差在2、3流道和7、8流道处最大,而3、4、5、6这几个流道间流量差距较小,这说明物流分配存在不均匀性。以雷诺数为2151时为例进一步描述这种物流分配不均匀性,如表2所示,流量的范围是0.0440~0.2208kg/s,最大流量是最小流量的5倍,流量偏差最大达到了近70%,这充分说明各流道实际的流量与理论的流量有着相当大的差距。

图4 各流道流量分布图
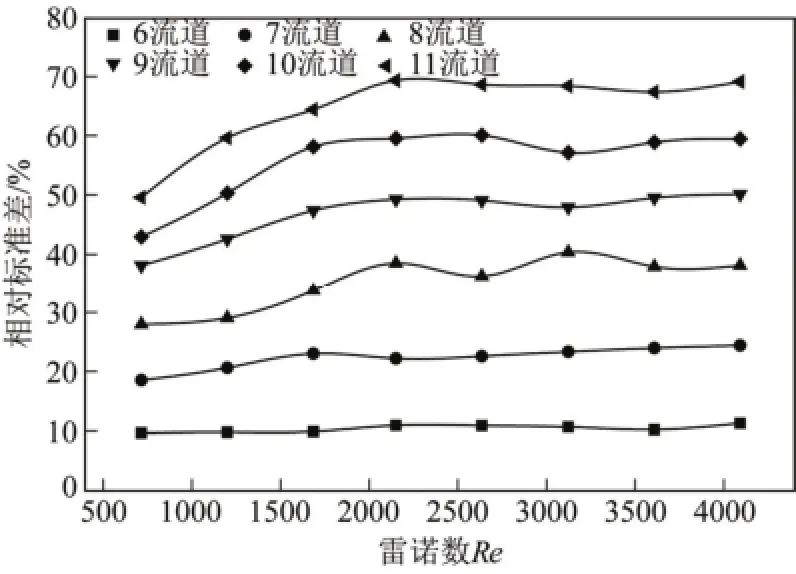
图5 各流道换热器相对标准差
图5为不同雷诺数下各流道换热器的相对标准差,雷诺数越小相对标准差变化越大,随着雷诺数的增大相对标准差先是逐渐增大的,而后逐渐趋于稳定,这说明雷诺数越大,越容易使物流分配不均匀性增加,但是不均匀性不是无限增大的,它最终趋于稳定。此外,在等雷诺数情况下,流道数越多,其相对标准差越大,物流分配越不均匀[13]。
2 物流不均匀性的影响
以上分析得出:板壳式换热器壳程存在较为严重的物流分配不均匀现象,这种分配不均匀性造成的影响,以下将选取9流道板壳式换热器各雷诺数情况下和其他流道换热器雷诺数为2151的情况下的数据,从传热效率、压降和效能三方面进行分析。

表2 流量偏差

表3 9流道换热器传热效率
2.1传热效率分析
传热效率是实际传热量与理论最大传热量的比值,一般由式(10)、式(11)表示。

式中,η为传热效率;Q、Qmax和Qi分别为实际传热量、理论最大传热量和i流道的传热量,W;Ti和To分别为流道的入口和出口温度,K。
表3、表4分别为9流道换热器在各个雷诺数下和雷诺数为2151时各流道数的换热器壳程总传热量与计算所得理论最大传热量及其传热效率。从表3、表4传热效率的分析结果不难发现,9流道换热器在不同雷诺数下传热效率在97.58%~99.07%范围内,而雷诺数在2151时各流道数的换热器传热效率在97.58%~99.43%这个范围内,虽然各流道的物流分配并不均匀,各流道的传热量也大不相同,但是对换热器整体而言,其总传热量很接近理论传热量,并没有发生大的偏移,模拟结果显示其最大偏移量在3%以内,也就是说流速分布不均匀对换热器的传热性能影响很小,这个结论也十分吻合邓先和等[7]的研究结果。通过对流换热公式,可以很好地解释传热量变化较小的原因见式(12)、式(13)。
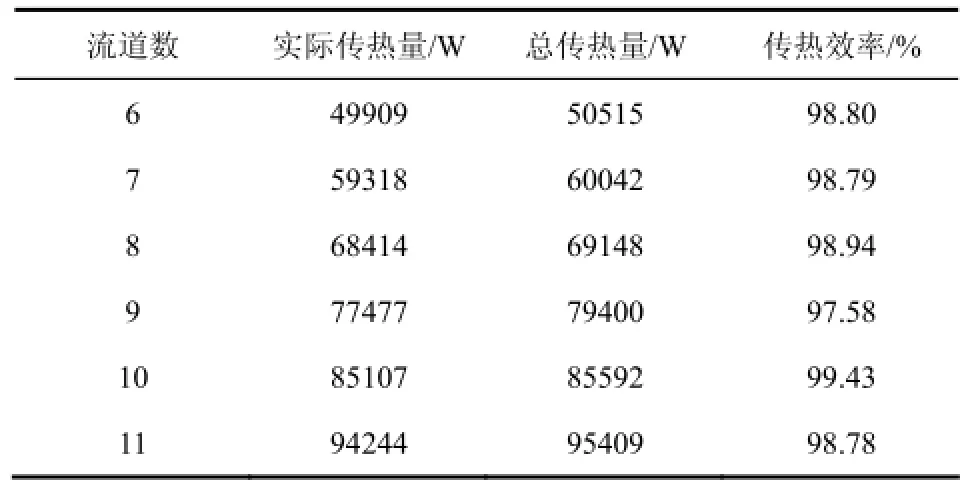
表4 各流道换热器传热效率

式中,α为对流换热系数,W/(m2·K);λ为热导率,W/(m·K);de为当量直径,m;μ为动力黏度,kg/(m·s);Re和Pr分别为雷诺数和普朗特数;v为流速,m/s;C、m和n分别为系数、普朗特数指数和雷诺数指数。
对于每个流道而言,对流换热系数α与流速v的n次方成正比,若n=1,α与v同时变化,此时虽然每个流道流速不同,传热也量不同,但是对出口温度没有影响,所以总传热量不变。实际上n<1,因此流速不同对出口温度会产生影响,尽管如此,由于流速越大流体热容也越大,因而热容与对流传热系数是同向变化的,故出口温度的变化不会太大,那么总传量的变化就会很小[7,14]。
2.2压降分析
理论上来说,压降的计算公式见式(14)、式(15)。

式中,ΔP为换热器的压降,Pa;Eu为欧拉数;b和d分别为系数和雷诺数指数。
首先,根据式(14)可知随着流速的增大压降逐渐增大,这一点是肯定的,这里便不作流速变化导致压降增大的相关分析。其次,对于同一板型的换热器其欧拉方程式是不变的,而计算雷诺数时,当量直径不变、温差改变不大时流体的动力黏度、密度均可视为不变,模拟时,各不同流道个数的换热器所设置的入口速度保证理论上各个流道内具有相同流速,因此欧拉数可看作恒定不变的,在理想状况下所有流道具有相同的压降,但是欧拉公式是通过实验获得的,因此不能通过直接计算获得,所以无法直接比较各流道压降与理论压降。但是理论上物流分配均匀时,每个流道压降是相同的,可以将模拟获得压降求平均值,比较各流道数换热器单流道压降的平均值即可发现压降的变化[15-16]。
图6中所示数据表明,随着流道数的增加,各流道的平均压降增加,这也就是说由于物流分配不均匀的存在,压降明显增加,且流道数越多,压降增加量越大。从式(14)也可以很好解释,由各流道的压降ΔP与流速v2成正比例的关系可知,从数学意义上出发,各流道v相等时总的压降是最小的,而各流道v的差距越大时,其总压降也就越大。
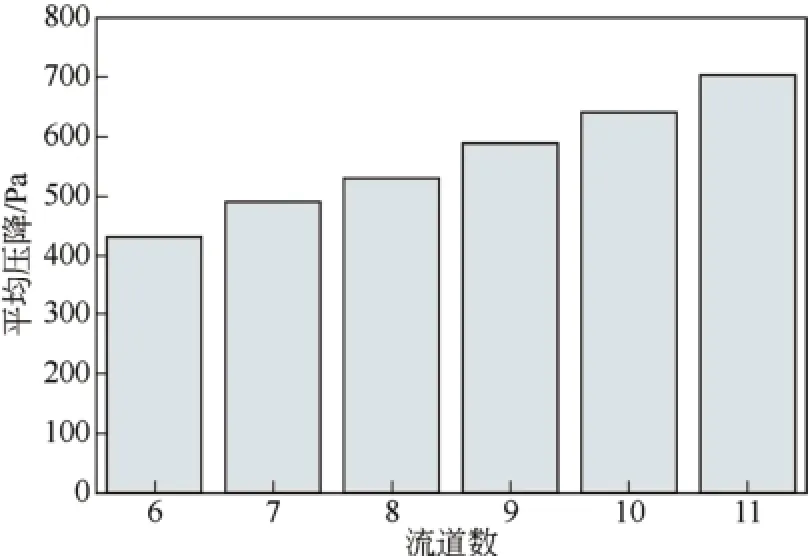
图6 单流道平均压降
2.3效能分析
理想状况下,换热器的效能可表示为式(16)。但是由于物流分配不均情况的存在,各流道的温度分布并不相同,因此采用式(17)方法求解效能。
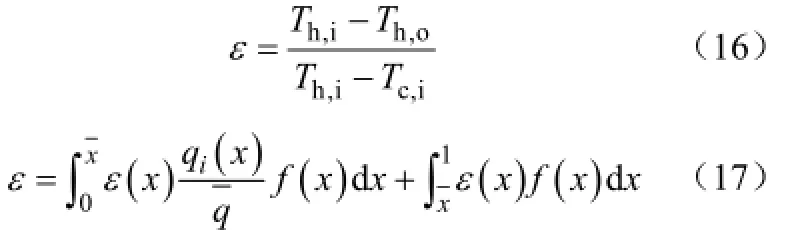
式中,ε为效能;下标h和c分别表示热流体和冷流体;f(x)为流量分布密度函数;为各流道的效能分布函数,对于流量小于平均流量的流道,对于流量大于平均流量的流道
由于流道数一定,各参数均为确定值,因此将该式离散化,见式(18)。
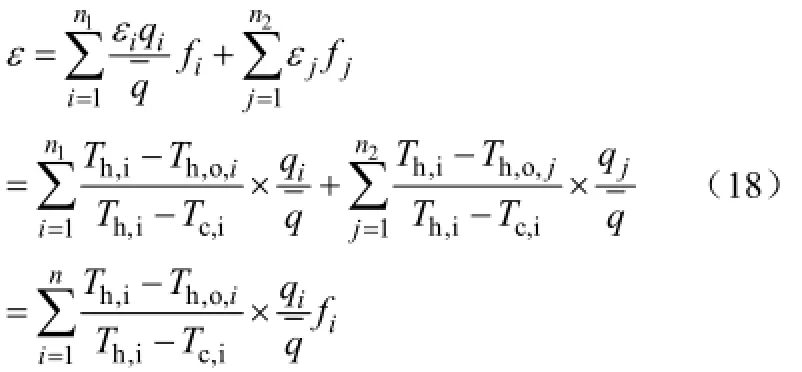
式中,i和j为流道的序号;n1、n2分别为小于平均流量和大于平均流量的流道数,n=n1+n2。此时fi=1/n,理论效能根据式(16)计算,再根据式(18)计算各换热器的实际效能。图7为所不同雷诺数下实际效能、理论效能与效能下降[3]。

图7 效能与效能下降
由图7不难看出,理论效能普遍高于实际效能,这说明由于物流分配不均性的存在,导致了换热器的效能下降。同时,随着雷诺数的增大,效能的下降量也随之增大,且增大趋势为由迅速趋向于缓慢。但是效能的下降量并不是无限增大的,原因在于,当流道数过大时,边缘流道流量所占比例越小,根据式(18)可知,即使单流道效能再高,由于流量太小,对于换热器整体效能影响也就很小,所以流道数越大,边缘流道对整个换热器效能的影响越来越小,整体效能下降量也就趋于不变。
3 物流不均匀性的优化
模拟与分析结果表明,板壳式换热器壳程入口存在严重的物流分配不均匀性,虽然这种物流分配不均性对总的传热量影响很小,但是却可以导致换热器的压降增大,也使得换热器的整体效能降低,这无疑影响换热器的整体性能,使得生产和使用成本的增加,因此有必要对其进行优化设计,本文以9壳程流道的板壳式换热器为例进行优化。
3.1壳程结构优化设计
板壳式换热器的壳程通道是由筒体、导流块以及板束所包夹区域,壳程起到相当于封头的作用,在此处考虑到流体的快速扩散在入口处加装一个封头来增大流动通道空间。在通道内加装一个圆弧状条纹板来强制分流,流体的流量分布特性为:在2、3和7、8流道间流量差距较大,在1、2和8、9流道内流量太小,故而希望减小中心5流道入口宽度,增大1、2、3和7、8、9流道宽度来调节流量,而采用弧状板片的目的是使流体不会垂直冲击板片从而减小了流动阻力,而一定的倾斜度又使流体更容易向通道四周扩散。
经过反复优化模拟后,获得的数据为:封头直径为50mm,长度97mm,圆弧状条纹板直径为240mm,宽度分别为1.8mm、2mm、2.6mm、3.2mm、3mm。该设计具体形式如图8所示,图9为条纹板片示意图。
3.2优化的模拟与分析
采用与1.3节相同的边界条件进行数值模拟,模拟后流体速度矢量图如图10所示,各流道速度分布云图如图11所示。
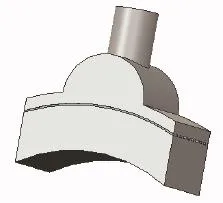
图8 优化设计示意图

图9 条纹板示意图
观察图11可以发现,各个流道流体在相同位置上的流速分布较为一致,流道由中间向两侧流速逐渐有增大趋势,这很好地说明了这种条纹板可以使物流分配更为合理,各流道物流分配均匀程度提高,此外流体在导孔上方流道流入较少,降低了流体对导孔造的冲击。该优化设计之所以可以使物流分配更加均匀,一方面,增加的封头可以使流体在流出管道后能够有充足的空间来向四周分散;另一方面,条纹宽度的变化使得流体在窄条纹处受到较大限制,部分流体由于截面积的减小而无法通过该处,被迫向宽条纹处流动,从而实现分流[17-18]。
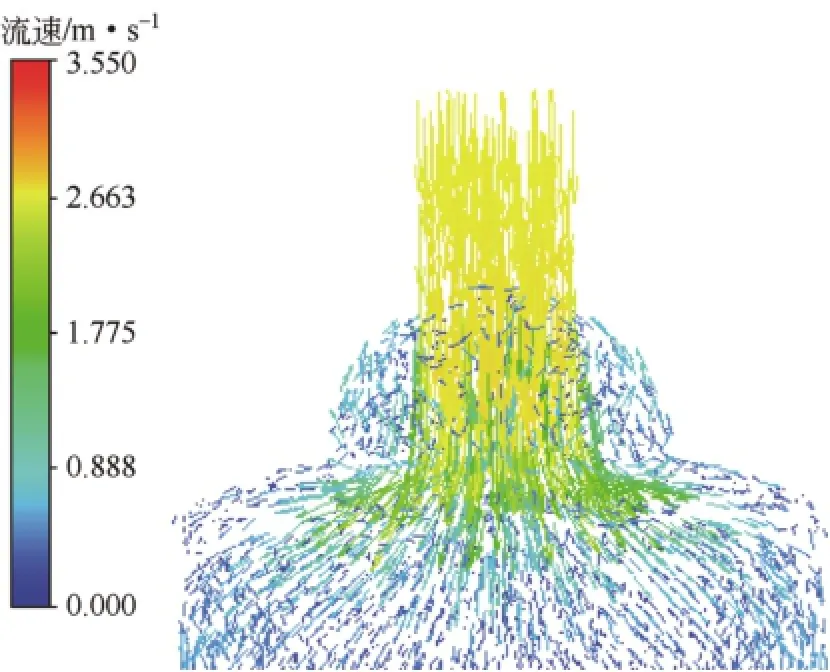
图10 流速分布矢量图

图11 流道入口处流速分布云图
3.2.1物流分配不均匀性分析
表5为该板壳式换热器雷诺数为2151时不同流道内流量与流量偏差,雷诺数2151时流量偏差范围由-69.95%~50.82%降低到-2.20%~1.69%,这说明各流道流量的差距非常小,都十分接近平均流量,因此物流分配均匀性提高明显,结合图12和表6也可以知,优化后的换热器雷诺数变化较大,各流道流量的差异也很小,相对标准差在0.98%~2.22%范围内,这充分证明该优化使各流道流量趋向于平均,改善了板壳式换热器壳程物流分配不均匀性。
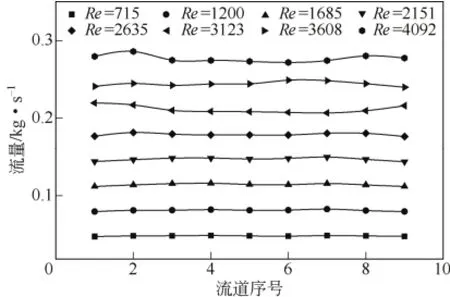
图12 各流道流量分布图
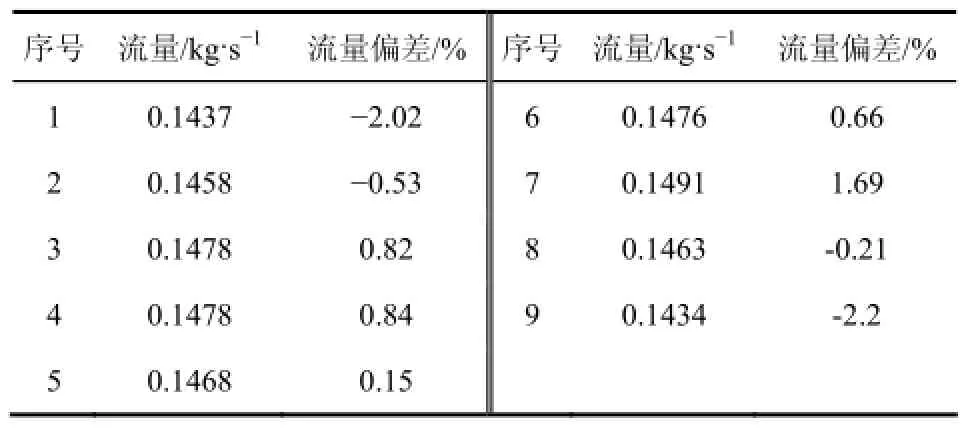
表5 流量偏差
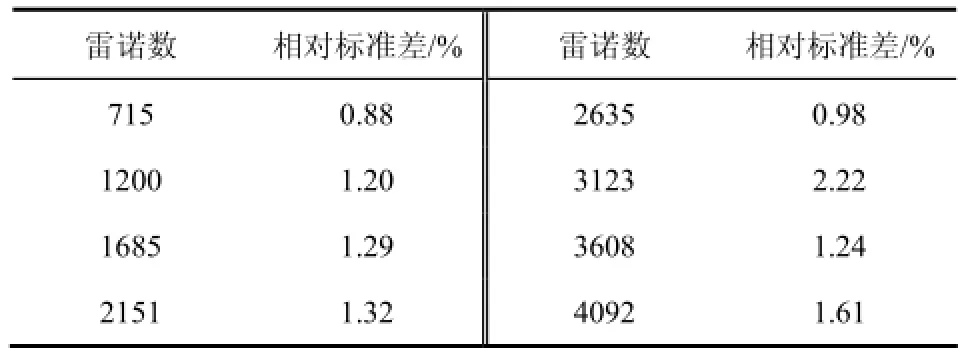
表6 相对标准差
3.2.2压降分析
表7所示为优化前后压降的变化,虽然在圆弧状条纹板处的压力损失会有所增大,但是就换热器整体而言,优化后的换热器由于物流分配更为均匀,各流道的压降也近乎相等,因而优化后换热器总压降有所降低。
3.2.3效能分析
由式(16)、式(18)计算效能,结果如表8所示。实际效能仍然低于理论效能,但是优化设计后换热器的效能下降量在2.96%~6.36%之间,显然与优化之前效能下降量4.70%~18.10%的结果有了大幅度的提高,图13可清晰地表现出优化前后的差异。
由以上分析可得出,板壳式换热器壳程的优化设计能够较好地解决换热器的流量分布不均情况,改善换热器入口处的物流分配不均匀性,在降低压降的同时,提高换热器的整体效能。
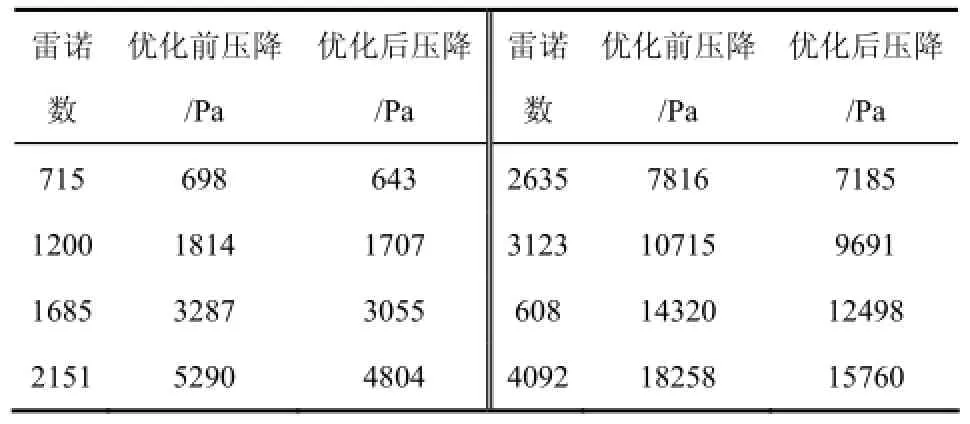
表7 压降对比
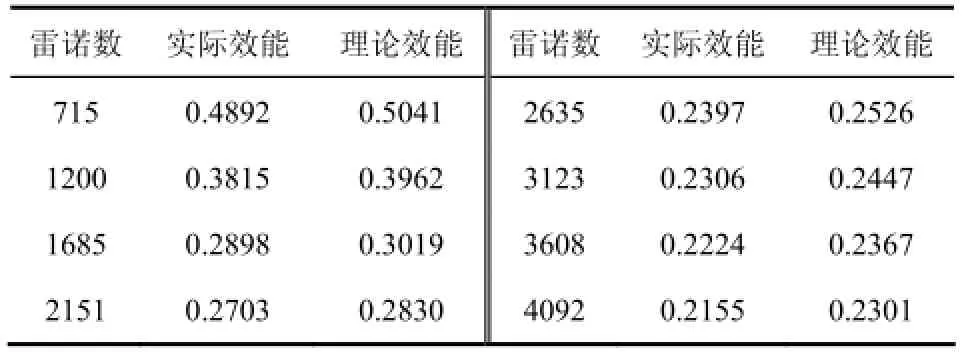
表8 效能对比
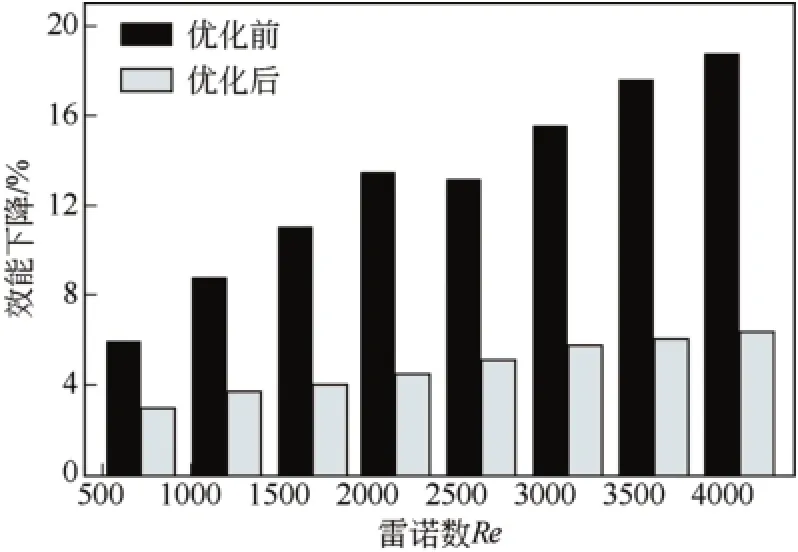
图13 效能下降对比图
4 结 论
通过对板壳式换热器壳程进行数值模拟,发现壳程各流道内流量的分布差异很大,存在严重的物流分配不均匀现象,并且由于这种物流分配不均匀现象的存在,使得换热器的效能下降非常明显,而且会造成压降的增加,但是这种物流分配不均匀现象对于总的传热量影响非常小,所研究换热器的换热效率下降不超过3%。
本文提出了一种对板壳式换热器壳程的优化设计,在入口管道接口加装半圆形封头,同时在壳程通道设置圆弧状条纹板。模拟结果显示这种优化后的板壳式换热器流量偏差降低到3%以内,物流分配不均匀现象得到明显改善,同时换热器效能的下降量大幅度降低,并且能降低换热器的压降,具有一定的参考价值。
[1] Fleeting R B. The effects of flow distribution in parallel channels of counter-flow heat exchangers[J]. Advances in Cryogenic Engineering,1967,12(2):352- 362.
[2] 焦安军,厉彦忠,张瑞,等. 物流分配的不均匀性对紧凑式换热器效能的影响[J]. 西安交通大学学报,2001,35(3):265-269.
[3] 焦安军,厉彦忠,张瑞,等. 封头结构对板翅式换热器物流分配不均匀性的影响[J]. 化工学报,2003,54(7):906-912.
[4] 张哲.板翅式换热器物流分配特性及换热的研究[D]. 西安:西安交通大学,2004 .
[5] 赵镇南. 流量分布不均匀对板式换热器传热性能的影响[J]. 化工机械,2003,30(1):1-4.
[6] 赵镇南. 流量非均匀分布对板式换热器传热性能影响[J]. 石油化工设备,2003,32(3):18-22.
[7] 邓先和,王杨君,黄德斌,等. 来流不均匀分布对换热器传热的影响[J]. 华南理工大学学报:自然科学版,2004,32(2):1-3.
[8] 文键,厉彦忠,周爱民,等. 板翅式换热器入口结构的改进[J]. 吉林大学学报:工学版,2006,36(2):177-182.
[9] 姚成林,张浩. 带有导流翼的板翅式换热器封头结构优化设计研究[J]. 矿业安全与环保,2014,41(5):40-42.
[10] 仇嘉,魏文建,张绍志,等. 基于CFD数值模拟的板式换热器分配器性能研究[J]. 机械工程学报,2010,46(14):130-137.
[11] 王福军. 计算流体动力学分析——CFD软件原理与应用[M]. 北京:清华大学出版社,2004:113-126.
[12] 刘巍,王娟,朱春玲. 换热器流量分配不均匀性评价方法的比较[J].制冷与空调,2013,13(3):93-96.
[13] 王江,厉彦忠,张哲,等. 封头结构对板翅式换热器温度分布特性的影响[J]. 化工学报,2005,56(8):1413-1418.
[14] Habib M A,Mansour R Ben,Said S A M,et al. Evaluation of flow maldistribution in air-cooled heat exchangers[J]. Computers and Fluids,2009,38:677-690.
[15] 史美中,王中铮. 热交换器原理与设计[M]. 第4版. 南京:东南大学出版社,2012:130-137.
[16] 刘家瑞,赵巍,黄晓东,等. 板壳式换热器传热准则关系式的分析与实验研究[J]. 动力工程学报,2015,35(6):469-475.
[17] Ahmad M,Berthoud G,Mercier P. General characteristics of two-phase flow distribution in a compact heat exchanger[J]. International Journal of Heat and Mass Transfer,2009,52:442-450.
[18] Wen J,Li Y Z. Study of flow distribution and its improvement on the header of plate-fin heat exchanger[J]. Cryogenics,2004,44:823-831.
Numerical simulation and optimization on fluid flow distribution performance of plate and shell heat exchanger’s shell-side
LIU Jiarui1,ZHAO Wei1,HUANG Xiaodong2,ZHANG Hua1
(1School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;2Dongguan ARO Heat Energy Technology Co.,Ltd.,Dongguan 523053,Guangdong,China)
This research established the geometric models of the Shell-side of plate and shell heat exchanger(PSHE). Numerical simulations calculated the deviations and the relative standard deviation of the mass flow,the fluid flow distribution performances were analyzed,the influences of fluid flow distribution performance on heat transfer efficiency,pressure drop and effectiveness of PSHE were analyzed. To optimize the design,a head and circular shaped stripe plate installed at the entrance could improve the impacts of fluid flow distribution and improve the performances of plate and shell heat exchanger. It was concluded that the uneven fluid flow distribution on the shell-side of plate and shell heat exchanger could significantly decrease the whole performances and increase the pressure drop,while it had little effects on the heat transfer efficiency,with the offset of the total heat exchange capacity less than 3%. Moreover,the optimization design not only improved the distribution uniformity obviously,but also made the drop of effectiveness and pressure drop less significant.
plate and shell heat exchanger(PSHE);fluid flow distribution;heat exchange;numerical simulation;optimization design
TK 172
A
1000-6613(2015)10-3569-08
10.16085/j.issn.1000-6613.2015.10.008
2015-04-08;修改稿日期:2015-04-28。
国家自然科学基金项目(51176124)。
刘家瑞(1991—),男,硕士研究生,研究方向为板壳式换热器传热性能。联系人:赵巍,讲师,博士,研究方向为自复叠制冷和换热器传热性能。E-mail zw_cherry@163.com。

