船舶锚泊辅助动力定位的抗扰控制
雷正玲,郭晨,刘正江
(1.大连海事大学信息科学技术学院,辽宁 大连116026;2.大连海事大学航海学院,辽宁大连116026)
在锚泊辅助动力定位系统操作中,根据已知的风浪流海洋低频干扰的情况使用锚泊设备增加船舶的阻尼,使之初步定位,再利用推力器系统细调达到准确定位的目的[1]。锚泊设备对定位系统的贡献属于一种前馈控制,欲达到更高的定位精确度要求,必须实时解决船舶运动因大惯性、大时滞和强非线性[2]导致的系统不确定性,此时便需要引入反馈控制[3]。在工业领域占主导地位的控制方法是比例-积分-微分控制器(PID),因其算法简单、易于实施,被广泛应用于工程实际中。然而,对于一些控制精度和速度要求较高的场合,PID控制器因其只在系统误差出现时才会产生作用而显得有些被动。在理论科学领域,基于被控对象数学模型的现代控制理论蓬勃发展,硕果累累。但是由于建立一个精确的被控对象数学模型成本很高,目前能应用于工程实际的基于模型的控制方法很少。近年来,自抗扰控制技术[4-5]因其不依赖于精确的数学模型,且易于工程实现,已吸引了一些工业界巨头的关注[6-7],并开始逐步走向产品化,比如,2013年 4月,德州仪器在全球发布以自抗扰技术为核心的运动控制芯片[8]。在工业界应用的不断成功,证明了自抗扰技术的巨大潜力。本文提出一种控制参数少且不依赖于精确数学模型的自抗扰策略用于解决锚泊辅助动力定位系统的控制问题。
1 系统动力学模型
船舶运动控制的研究一般采用两种坐标系:惯性坐标系和附体坐标系。根据分离型建模机理(MMG),忽略前进、横移、转艏运动与垂荡、横摇、纵摇运动之间的耦合,假设附体坐标系的原点就取在船舶的重心上,全驱动船舶运动方程[9]可表示为

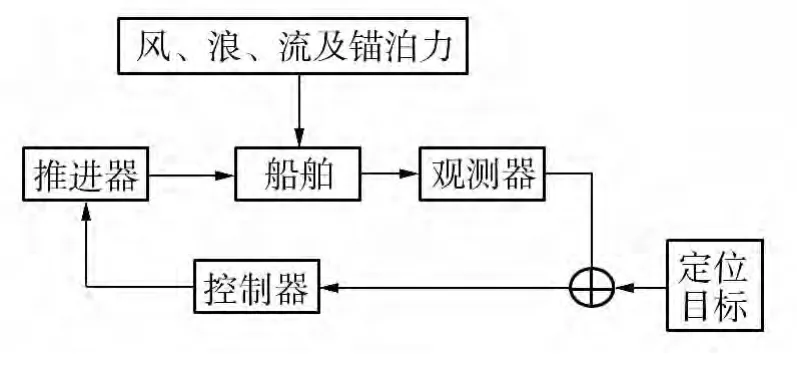
图1 动力定位系统框图Fig.1 Block diagram of dynamic positioning system
由于本文建立系统模型是为了设计控制器,所以锚泊力和力矩模型采用静态悬链力方程[11]表示即可,方程如下
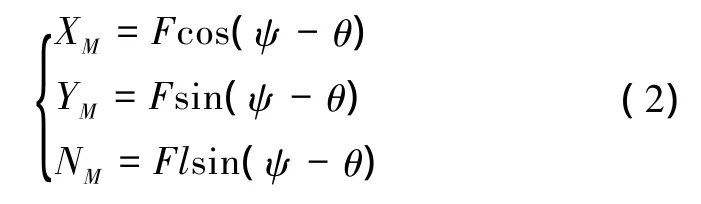
式中:F为锚链对船体作用的水平分力,ψ和θ分别为航向角和锚链方位角,l为锚孔至重心的距离。
本文考虑的低频海洋干扰模型[12]为

式中:Fe是缓慢变化的定常力,βe是干扰力变化的平均方向,(lx,ly)是干扰力在船舶上的作用点坐标,且
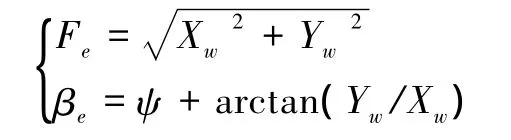
取船舶匀速运动这一平衡状态作为基点,即u0=V=C,将式(1)左端的刚体惯性力和右端的粘性力X、Y、N进行泰勒展开后取一阶小量,运动方程(1)可线性化为:
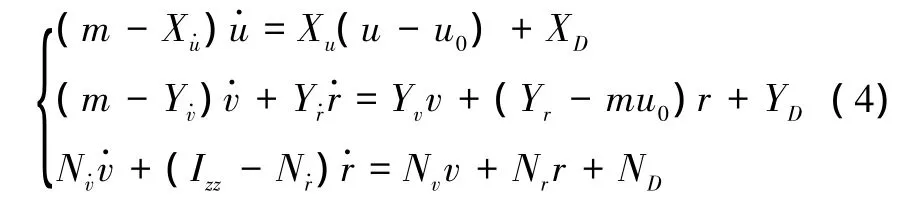
对于低速动力定位船舶,可取u0=0为平衡状态,此时式(4)简化为
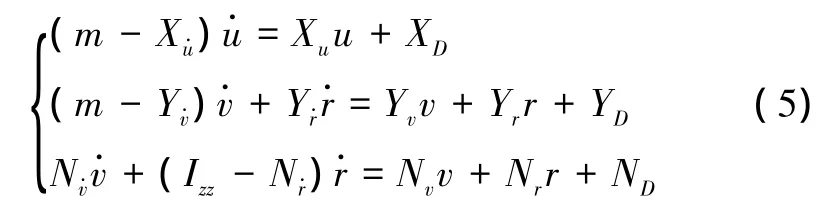
将方程(5)整理成状态空间形式为

式中:ν=[uvr]T表示船舶的速度矢量;τ=[XDYDND]T表示引起船舶运动的总力和总力矩;τT=[X Y NT]T表示推力器产生的力和力矩;τM=[XMYMNM]T表示锚泊系统产生的力和力矩;τw=[XwYwNw]T表示干扰力和力矩。

速度矢量ν与位置矢量η=[xyψ]T的关系可表示为

辅助动力定位系统的任务,就是借助于锚泊系统和推进器系统抵消海洋干扰的影响,使船位η定位在期望的位置η*上。假设锚泊系统模型(2)、海洋干扰模型(3)以及系统数学模型(6)、(7)是精确反映客观现实的,那么使船舶精确定位到期望位置η*所需的推力和力矩[X Y NT]T可以通过解方程组(2)、(3)、(6)、(7)计算得出。然而,从建模过程可发现,这些数学模型是建立在一系列假设和线性化基础之上的,由此忽略掉的不确定性和系统未建模动态使得基于模型设计的解析控制器的鲁棒性得不到保证。所以,要想实现船舶定位,需先处理船舶运动的不确定性。
2 自抗扰控制策略
为了使问题更加清晰,联立式(6)、(7)可得:

其中,A=MR-1(ψ),B=MR·-1(ψ)+DR-1(ψ)。下面对系统(8)中的每一个回路引入虚拟控制量u=,i=1,2,3,则系统(8)中各子回路可以表示为

式中:f称为系统的总扰动,包括系统未建模动态、系统不确定性和外部海洋扰动,假设f二阶可导,即k。接下来,若用一个四阶扩张状态观测器(ESO)[4-5]来估计y、y·、f和g,ESO的表达式如下:
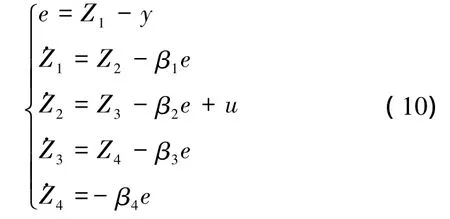
若把观测器的4个极点都配置在ωo,则其特征方程为:λ(s)=s4+β1s3+β2s2+β3s+β4=(s+ωo)4,也即 β1=4ωo即适当调节 ωo,可使Z1→y,Z2→·y,Z3→f,Z4→g。
得到系统总扰动的估计值后,可以在控制器中将其补偿掉,补偿算法为

理想情况下,补偿后的系统(9)成为一个积分串联型对象,表达式为

这种解决问题的思路即为自抗扰控制[4]。
考虑船舶控制系统采样间隔相对偏大的特征,为使控制器补偿扰动的效果更好,利用估计出的扰动微分g,可近似获得下一采样时刻的扰动信息:

其中,T为采样周期。并在闭环系统里将下一采样时刻的扰动补偿,此时式(11)改写为

u0采用简单的PD控制即可,表达式为

控制器增益选择[5]为:

综上所述,若ξ固定,动力定位控制系统的每一个回路都只需调节参数ωo和ωc。请注意,u是虚拟控制量,实际的控制量(τT)i还需通过式u=(A-1τT)i进行计算求得。说明为了更高精度地逼近扰动信息,可以通过估计更高阶扰动信息然后用泰勒多项式得到扰动信息模型,通过这种方法估计扰动的观测器被称为GPI观测器[13]。
3 仿真研究
本文以救助船“北海救115”轮为研究对象,根据其实船数据建立动力定位数学模型。其实船基本数据如表1所示。

表1 北海救115轮的基本参数Table 1 Basic parameters of BeiHaiJiu 115
采用Clarke整理的线性流体水动力导数估算公式[14]得到模型(6)中的M、D矩阵。

其中,Lw为船舶水线长,本文粗略取为船长。
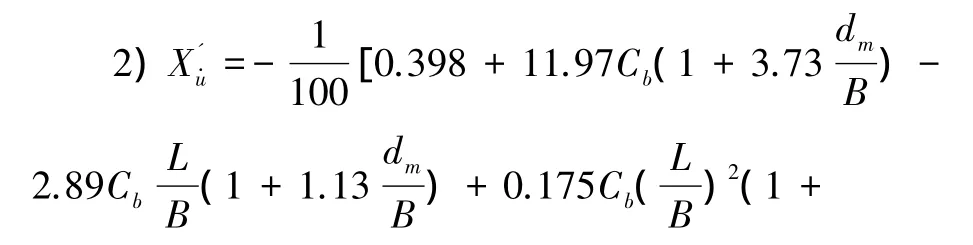

计算得115轮M、D参数分别为

3.1 仅用锚泊设备定位情况
假设海洋干扰模型的参数为:Fe=10(经一撇系统无量纲化),βe=120sin(0.3t),(lx,ly)=(20 m,5 m)。假设锚链方位角θ=30°,锚孔至重心的距离l=37.5 m,且锚机工作在工作负载。锚泊设备定位的曲线如图2所示。

图2 仅靠锚泊设备定位的船舶位置Fig.2 Ship positioning only by mooring system
从图中可以发现锚泊设备仅能使船舶定位在一个小的变化范围之内,但没法使之精确定位,船位随着海洋干扰的作用而不断地缓慢变化。欲使船舶定位在一个精确的位置,需在闭环的反馈系统中靠推力器作用实现。
3.2 锚泊辅助动力定位自抗扰控制
设定船舶的初始位置是[0 0 0]T,假设海洋干扰模型的参数为:Fe=500(经一撇系统无量纲化),βe=120sin(0.3t),(lx,ly)=(20 m,5 m),希望船舶在持续的外扰作用下保持船位不变。3个回路控制器参数为,纵荡回路:ωo=50,ωc=15;横荡回路:ωo=50,ωc=15;艏摇回路:ωo=150,ωc=50。船舶的位置曲线如图3所示,ESO观测到的3个回路的总扰动如图4所示,控制器3个回路的输出如图5所示。
从图中可以发现,即使在外扰持续作用下,经过对ESO观测出的扰动的实时补偿,控制器的输出很快减小并维持在0且船位被精确定位在期望的位置上,这意味着在达到控制目标的前提下,控制器的下级执行机构,即115轮的5个推进部件,磨损量得以控制在一定小的范围内,减小了能量损耗,提高了经济性。
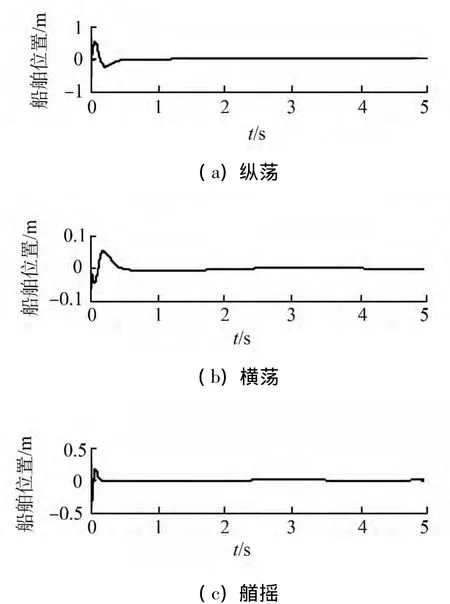
图3 锚泊辅助动力定位的船舶位置Fig.3 Ship positioning by mooring-assisted DP system

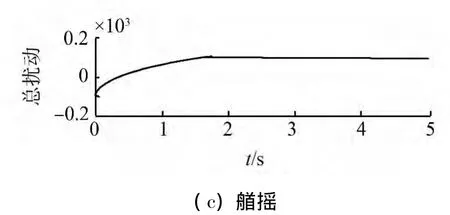
图4 ESO观测到的系统总扰动Fig.4 Total disturbance estimation via ESO

图5 控制器输出Fig.5 Control outputs
3.3 鲁棒性测试
为了进一步测试锚泊辅助动力定位自抗扰控制的鲁棒性,将控制对象变更为一艘供给船,此供给船模型数据来源于挪威科技大学GNC实验室的几次海试,其中惯性矩阵M和阻尼矩阵D如下所示[15],保持控制器参数和扰动环境不变:

仿真结果如图6所示,图6是同一控制器应用于另一船舶的位置曲线。可以看到,在持续干扰作用下,供给船能准确地定位在期望的位置上,证明了自抗扰控制器的强鲁棒性和适应性。这为由不确定性导致的建模不准确的船舶运动控制问题提供了一条全新的解决思路。
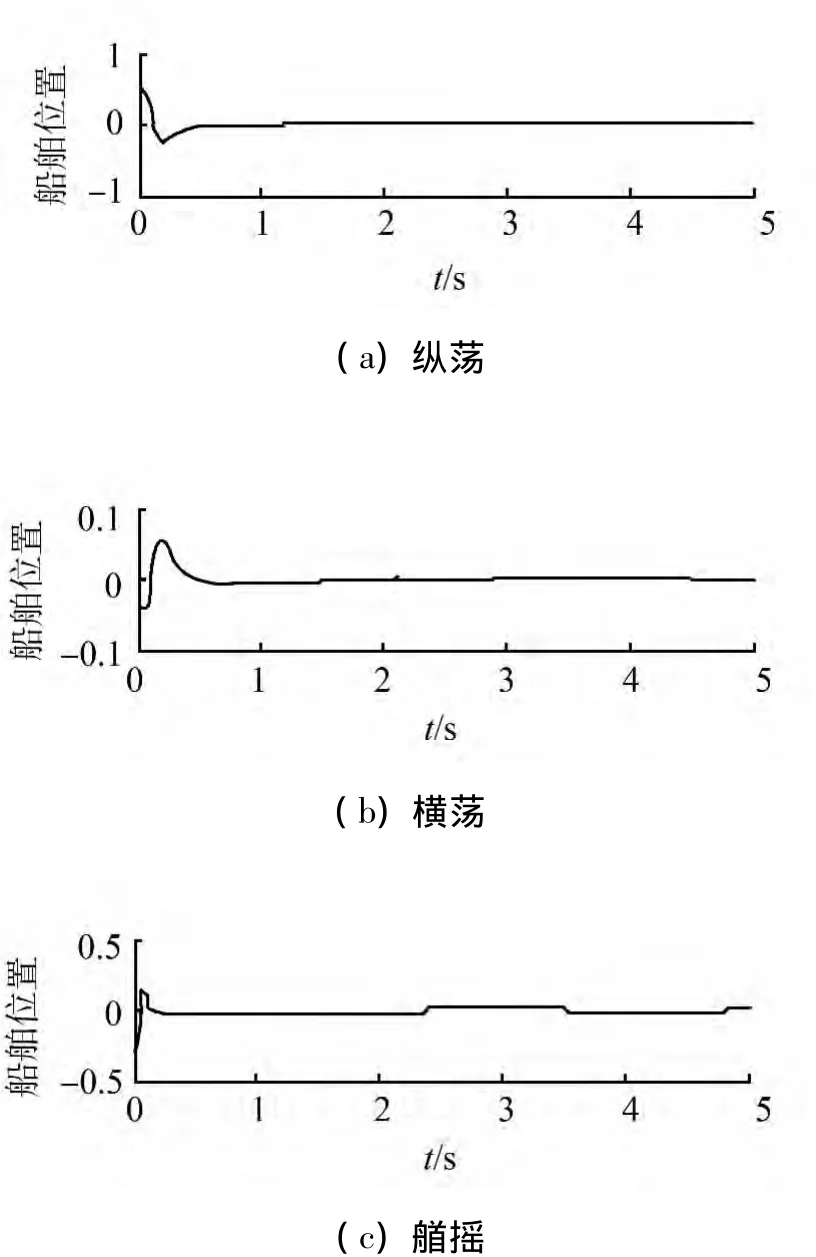
图6 同一控制器应用于另一船舶的位置曲线Fig.6 Another ship’s position by the same controller
4 结论
本文提出了一种锚泊辅助动力定位的抗扰解决方案,将船舶运动系统的未建模动态、模型不精确性以及锚泊系统未能全部抵消掉的海洋低频扰动统统归结为系统的“总扰动”,考虑系统的计算延时,用一个高阶扩张状态观测器将系统下一采样时刻的总扰动估计出来,并在闭环中将其补偿掉。这种方案控制参数少、简洁且易于工程实施,本文以一艘救助船和供给船为对象,验证了所提方法的有效性和鲁棒性。
扩张状态观测器效能的好坏是影响自抗扰控制应用成败的关键因素,而外界干扰和不确定性是复杂多变的,如何提高ESO的估计能力使其适应不同的实际问题是下一步工作的重心。另外,船舶动力定位控制问题是一个复杂的系统工程,为了把一个实际的工程问题解决好,接下来应该深入了解工程实际中的疑难问题并将其描述成理论工作者易于理解的数学语言,比如船舶动力定位问题中的因执行机构引起延时现象等,在此基础上才能展开有意义的理论研究。
[1]NGUYEN D T,SORENSEN A J.Setpoint chasing for thruster-assisted position mooring[J].IEEE Journal of O-ceanic Engineering,2009,34(4):548-558.
[2]YANG Y,ZHOU C,REN J.Model reference adaptive robust fuzzy control for ship steering autopilot with uncertain nonlinear systems[J].Applied Soft Computing,2003,3(4):305-316.
[3]ENGQUIST B.Mathematics unlimited-2001 and beyond[M].Springer-Verlag Berlin and Heidelberg GmbH & Co.K,2001:189-220.
[4]HAN Jingqing.From PID to active disturbance rejection control[J].IEEE Transactions on Industrial Electronics,2009,56(3):900-906.
[5]GAO Z.Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American Control Conference.Denver,USA,2003:4989-4996.
[6]Achieve improved motion and efficiency for advanced motor control designs in minutes with TI's new InstaSPIN(TM)-MOTION technology[J/OL].The Wall Street Journal.(2013-04-18). http://online.wsj.com/article/PR-CO-20130418-907338.html?mod=googlenews_wsj.
[7]HERBST G.A simulative study on active disturbance control(ADRC)as a control tool for practitioners[J].Electronics,2013,2:246-279.
[8]TMS320F28069M,TMS320F28068MInstaSPIN(TM)-MOTION Software Technical Reference Manual[S].Texas:Texas Instruments,2013:75265.
[9]贾欣乐,杨盐生.船舶运动数学模型:机理建模与辩识建模[M].大连:大连海事大学出版社,1999:22-27.
[10]RYU S,KIM M H.Coupled dynamic analysis of thrusterassisted turret-moored FPSO[C]//OCEANS 2003.Proceedings.San Diego,CA,USA,2003:1613-1620.
[11]候建军,东昉,石爱国,等.锚泊状态下锚链作用力的计算方法[J].大连海事大学学报,2005,3(4):10-14.HOU Jianjun,DONG Fang,SHI Aiguo,et al.Calculation method of chain force on ship at anchor[J].Journal of Dalian Maritime University,2005,3(4):10-14.
[12]FOSSEN T I,STRAND J P.Nonlinear passive weather optimal positioning control(WOPC)system for ships and rigs:experimental results[J].Automatica,2001,37(5):701-715.
[13]MORALES R,SIRA-RAMIREZ H.Trajectory tracking for the magnetic ball levitation system via exact feedforward linearisation and GPI control[J].International Journal of Control,2010,83(6):1155-1166.
[14]刘胜.现代船舶控制工程[M].北京:科学出版社,2010:32-33.
[15]FOSSEN T I,SAGATUN S I,SORENSEN A J.Identification of dynamically positioned ships[J].Control Engineering Practice,1996,4(3):369-376.

