转向器最大齿条力的计算与验证

王文建，张雷（江淮汽车技术中心乘用车研究院，合肥236001）

转向器最大齿条力的计算与验证

王文建，张雷
（江淮汽车技术中心乘用车研究院，合肥236001）

乘用车转向系统的匹配设计中，齿条力的确定至关重要，最大齿条力的计算为转向系统匹配设计提供依据。本文结合实际工作经验，对转向系统最大齿条力的计算进行研究和验证。该方法在CAE整车模型建立之前即可计算出最大齿条力值，从而节省开发时间。

齿条力；转向阻力矩；回正力矩；转向器

转向系统的匹配是汽车设计中一项非常重要的工作。转向系统匹配工作不仅要保证其转向的功能，还要重点考虑轻便性、成本及使用可靠性。在匹配设计的过程中，需要确定许多关键参数［1］：转向操纵力矩、转向器线角传动比、最大齿条输出力；对液压助力转向系统来说，还需确定液压缸内活塞有效受力面积、系统的最高压力、泵的流量曲线设定、转向器阀特性曲线等；对电动助力转向系统来说，还需要确定电机参数、蜗轮蜗杆传动比、电流-扭矩关系曲线等。而最大齿条力是确定其它参数的必要条件，也是最难确定的一个参数。匹配使用的齿条力较小，后期就要进行重复性工作，变更带来了成本上升；匹配使用的齿条力较大，却造成系统的设计助力过大，造成了性能浪费和成本上升。

对此，本文重点介绍设计阶段最大齿条输出力的确定方法，以及在整车上对最大齿条输出力的测试方法；并以我司新开发的车型为例，验证计算方法的可靠性。

1　最大齿条力的理论计算

转向过程中需要克服原地转向阻力矩、回正力矩、转向系统阻力。根据经验，最大转向齿条力在原地转向极限处，因为此时转向阻力矩最大，回正力矩也最大。

1.1原地转向阻力矩的确定

原地转向阻力矩可根据经验公式［2-3］：

式中：f为轮胎和路面间的滑动摩擦系数，一般取0.7左右；Mr为转向阻力矩，N·m；G为前轴负荷，N；p为轮胎气压，MPa。

1.2重力回正力矩的确定

由于主销内倾和内移，前轮转动时将使车身有抬高的倾向，这种系统重力势能的提高会产生前轮的回正力矩。车辆回正时，汽车本身的重力就有使转向轮回复到原来中间位置的效果；而在转向时，就要克服这一回正力矩。

图1中［4-5］，σ为主销轴线OA与地面垂线的夹角，即主销内倾角；D为车轮中心C至主销轴线的距离，即主销内移量；WL大小等于左轮轮荷。当车轮转动时，车轮中心C在垂向的上下运动与重力回正力矩密切相关。

由图2，设车轮转过转角δ，轮胎印迹中心由E点移到F点，则横向水平位移量为

若不计能量损失，转动车轮需要作的功应等于重力势能的增加，即

对上式两端求导，可得转动车轮需要施加的绕主销的转矩为

1.3最大齿条力的计算

根据经验，转向梯形为瞬时复合几何运动梯形，不仅随着主销内倾角和后倾角变化，还伴随着转向器齿条移动而变化。可根据以下方法确定极限位置下的瞬时梯形：过j点做垂直主销的平面，与主销交于g点，同理得到h点，从而确定了空间状态下的转向梯形jghi，如图3所示。

图3中，ab为地面线；cd、ef为主销轴线；j、i为转向器拉杆外球节中心；k、l为转向器拉杆内球节中心。

将获得的空间梯形投影到地面转化为平面梯形，再通过几何关系求得左转极限位置下齿条位置如图4所示。图4中空间点在地面上的投影为齿条左转极限位置的投影点，k'k"为齿条左转行程。通过此种方法，可以求得极限位置转向节臂有效距离g'm，同时可以求得内轮转角∠j'g'j"和外轮转角∠i'h'i"。根据以上方法可以确定回正力矩需要的参数。

车轮绕主销旋转，转向器拉杆推动转向节臂，确定克服转向阻力矩需要的齿条力，需要确定空间转向梯形，将梯形投影到地面，计算出极限位置下内轮转向梯形有效作用力臂S（由于外轮作用力臂长于内轮作用力臂，考虑到匹配计算的齿条力要大于实际齿条力，在此按照内轮力臂进行计算）；在实际情况中，最大齿条力还包括在转向过程中需要克服的转向系统阻力Ff。转向系统阻力主要来自转向器，液压助力转向器的阻力与齿条的压块作用力和活塞密封阻力有关，一般在300 N左右；机械转向器的阻力较小，可按照200N计算。

由此得出克服阻力矩需要的齿条力为

1.4计算示例

以某车型作为示例，进行最大齿条力的计算（取该车型的3组前轴荷状态进行计算，然后与实测数据进行对比）。所需各参数如表1所示。

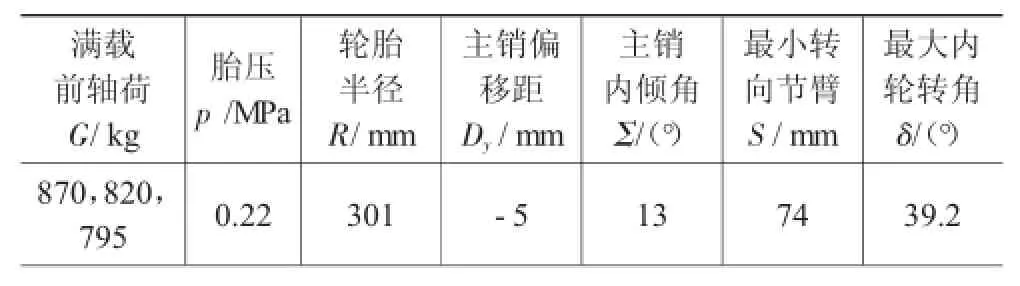
表1　相关参数值

以左侧为内轮、右侧为外轮进行计算，前轴负荷为870 kg时，原地转向阻力矩重力回正力矩因此，齿条力

同样可得满载前轴荷820 kg和795 kg时的齿条力分别为6 020N和5 762 N。

通过以上计算，得出3组某车型在不同配载情况下齿条力的理论值。

2　齿条力的测量验证

2.1测量方法简介

产品开发中，样车出来后需要对齿条力进行测试验证，采用应变电阻测量技术［6-7］，将电阻应变片贴在转向器左右横拉杆上，用树脂牢固包裹。齿条上粘贴的应变计组成测量电桥，当齿条产生微小变形后引起电桥电阻值变化，应变电桥电阻的变化转变为电信号的变化，从而实现齿条拉力和压力的测量。

2.2测量数据分析

本次某车型齿条力测量［8］共测得7组数据。其中前轴荷870 kg及前轴荷795 kg各测2组数据，前轴荷820 kg测得3组数据；由于数据较多，以下仅列出典型数据。

1）前轴荷870 kg状态下在原地转向的工况下测得的齿条力如图5所示。由于传感器存在零点漂移的情况，所以以上数据中，正转方向的齿条力最大值与反正方向的齿条力最大值相差较大，取其平均值。因此，前轴荷870 kg状态的实际齿条力为（6 718+6 162）/2=6 440 N，与其理论计算值（6 554N）相差114N。

2）前轴荷820 kg状态下在原地转向的工况下测得的齿条力如图6所示。

同样，可得出前轴荷820 kg状态的最大齿条力为（6 523+5 332）/2=5 928 N，与其理论计算值（6 020 N）相差92N。

3）前轴荷795 kg状态下在原地转向的工况下测得的齿条力如图7所示。同样，可得出前轴荷795 kg状态的最大齿条力为（5 830+5 380）/2=5 605N，与其理论计算值（5 762N）相差157N。

3　结论

由以上可知，各轴荷下的齿条力理论值与实测值之间的差值都在200N之内。该精度已经可以满足整车匹配设计中对理论齿条力的精度需求。本论文所提出的计算方法能够很好地满足转向系统匹配的要求，可以应用于实际的汽车设计之中。

该方法在汽车设计开发初期尤为适用。在整车CAE模型尚未建立时，无法通过CAE精确计算最大齿条力；而整车模型的建立需要耗费大量的时间和精力。但通过该计算方法可以得到最大齿条力的粗略值，也就可以更早地进行转向系统的匹配设计，从而大大节省开发时间。

［1］余志生.汽车理论［M］.5版.北京：机械工业出版社，2010.3.

［2］刘惟信.汽车设计［M］.北京：清华大学出版社，2001.7.

［3］耶尔森·赖姆帕尔.汽车底盘基础［M］.张洪欣，余卓平，译.北京：科学普及出版社，1992.

［4］陈家瑞.汽车构造［M］.北京：机械工业出版社，2011.6.

［5］细川武志.汽车构造图册［M］.北京：人民交通出版社，2005.1.

［6］宋文绪，杨帆.传感器与检测技术［M］.北京：高等教育出版社，2004.1.

［7］刘笃仁，刘靳，韩保君.传感器原理及应用技术［M］.西安：西安电子科技大学，2013.8.

［8］王丰元.汽车试验测试技术［M］.北京：北京大学出版社，2007. 12.

修改稿日期：2015-01-21

Calcu lation and Validation of M ax Rack Force for Steering Gear

WangWenjian，Zhang Lei
（Passenger Car Institute，R&D of JAC，Hefei236001，China）

Inmatchingdesign ofpassenger car steering system，the determination of rack force isextremely important，the calculation of themax force lays foundation for thematching design of steering system.According to the practicalwork experience，the authors research the calculation and validation of themax rack force for steeringgear. By thismethod，themax rack force can be calculated outbefore the car CAEmodel building，thus a lotof time is saved in thedesign.

rack force；steering resisting torque；aligning torque；steering gear

U463.43+1

B

1006-3331（2015）04-0034-03

王文建（1985-），男，底盘设计工程师；研究方向：研究转向系统。