具有交叉扩散的捕食食饵模型稳定性的分析
刘阳阳
(东华大学 理学院,上海201620)
具有交叉扩散的捕食食饵模型稳定性的分析
刘阳阳
(东华大学 理学院,上海201620)
研究了一类带有Leslie-Gower功能性反应的捕食食饵模型, 主要应用Routh-Hurwitz理论讨论了交叉扩散引起的稳定性变化, 建立了关于非平凡正平衡解稳定性的充分条件, 并通过数值模拟验证了相应的理论结果.
捕食食饵模型; Leslie-Gower功能性反应; 交叉扩散; 稳定性
在大多数描述扩散系统动力学的文献中, 自扩散对系统的影响往往是学者关注的焦点. 近年来, 越来越多的学者开始关注交叉扩散对系统的影响. 本文将考虑带有Holling-Ⅱ和Leslie-Gower功能性反应的捕食者食饵模型, 在这个模型中加入了自扩散项和交叉扩散项. 带有自扩散的模型如下:
其中:H和P分别表示被捕食者和捕食者在时间T的种群密度;D11和D22为自扩散系数;A1,B1,C1,K1,A2,C2和K2为系统参数并且都是正数. 借助文献[1]中的变换可以得到:
(1)
文献[1]研究了系统(1)当a=1和d11=1时的非平凡正平衡解的图灵不稳定和Hopf分支问题. 文献[2]研究了系统(1)当k1=1和k2=0时的非平凡正平衡解的稳定性、图灵不稳定和Hopf分支问题, 同时, 通过计算Hopf分支的方向, 得到了空间齐次周期解并且判断这些解是否稳定.
然而在自然界中, 生物种群不会漫无目的地向外扩散, 被捕食者想向捕食者密度小的方向运动, 捕食者向被捕食者密度大的地方运动. 事实上, 自扩散只能表示生物种群向外扩散, 不能够确切地描述生物趋利避害自然本性. 此时, 交叉扩散的出现就显得尤为重要. 考虑到生物种群的这种自然本性, 在本文中考虑如下模型:
(2)
其中:d11和d22为自扩散系数;d12和d21为交叉扩散系数. 文献[3]分析了带有Holling-II功能性反应系统中空间变量是一维和二维两种情形下的全局稳定性, 并分别得到了由自扩散和交叉扩散引起的斑图, 这里的扩散系数均是常数, 此外, 也研究了当交叉扩散系数是时间变量情形下非平凡正平衡解的稳定性. 文献[4]研究了当d11=d22=1时系统(2)非平凡正平衡解的图灵不稳定性, 在这种情形下的不稳定性只是由交叉扩散引起的. 另外, 交叉扩散也被应用到半干旱生态系统中, 用交叉扩散来描述半干旱系统中水分的流动. 除此之外, 交叉扩散还被学者应用于更多的模型[5-10].
本文利用文献[11]的方法研究系统(2)和(3)的稳定性及Hopf分支,具体分下面3种情形讨论交叉扩散对系统(1)非平凡正平衡解稳定性的影响: (1)d12=0,d21≠0; (2)d12≠0,d21=0; (3)d12≠0,d21≠0. 在第3种情形中, 相较于文献[4]限制d11=d12=1的讨论, 这里会分析交叉扩散系数取不同值的情形下对系统稳定性的影响.
1 一维情形正平衡点稳定性分析

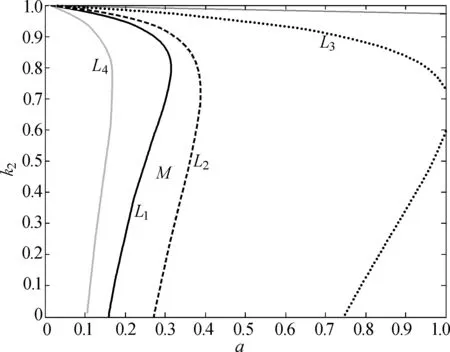
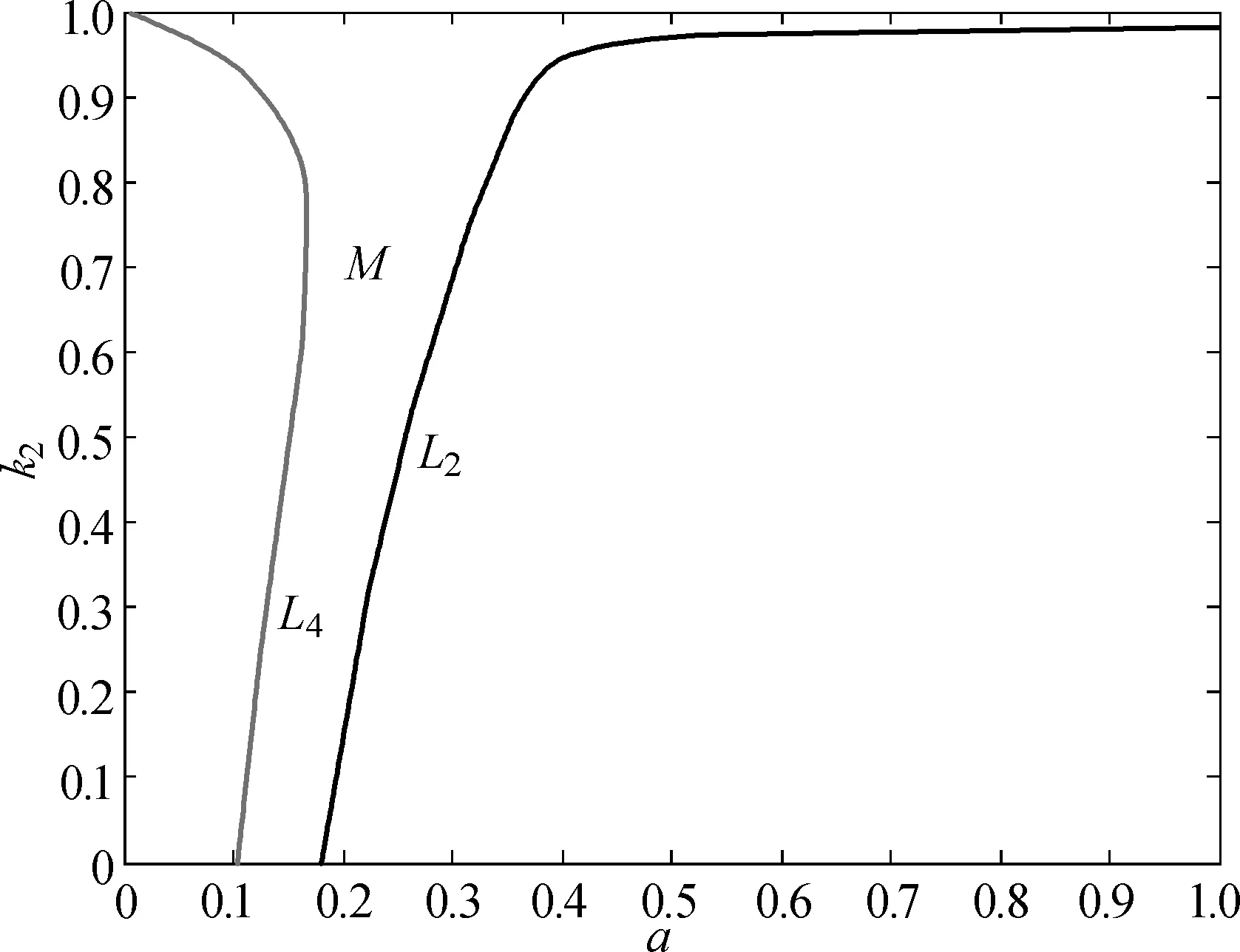
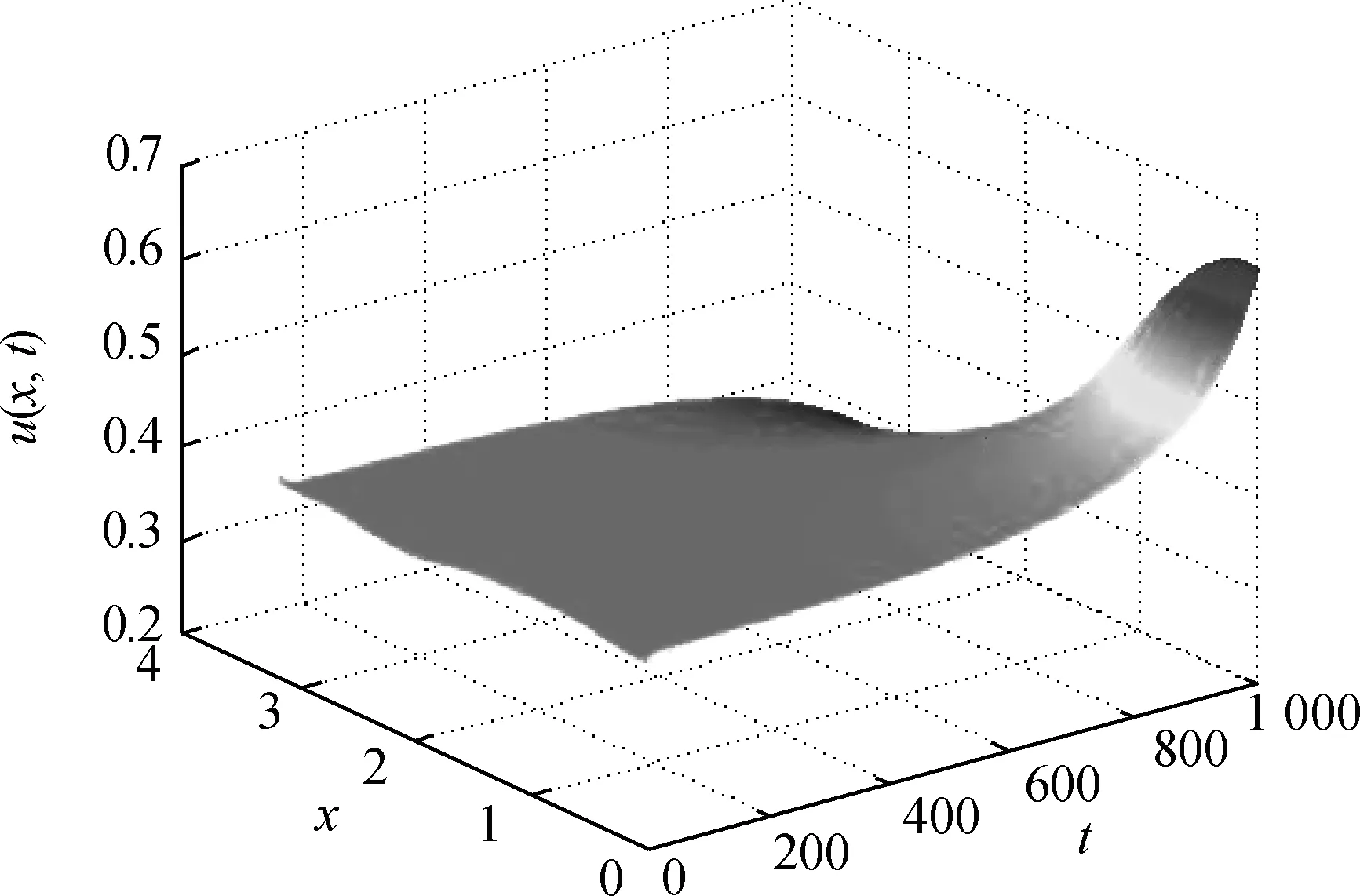
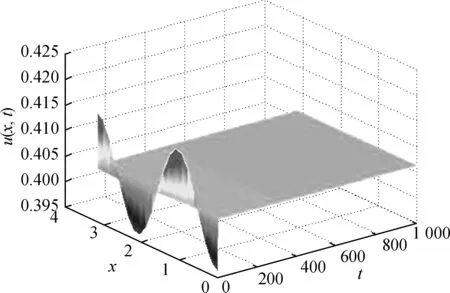
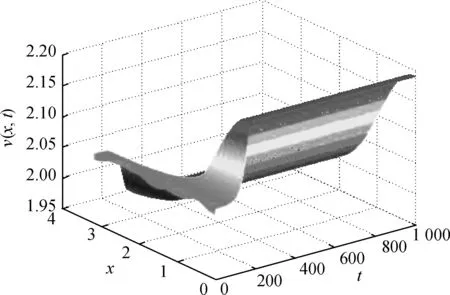
(H)bk2 成立, 有一个正的内部平衡点E*=(U*,V*), 这里 V*=U*+k2. 当空间变量是一维时, 系统(2)在E*处对应的线性系统为 (3) 下面寻求如下形式的特征函数: 和系统(3)的如下形式的解: 系统(3)的特征方程为 λ2-Tnλ+Dn=0, (4) 其中 c(s+e). (5) 假设 (6) 由式(6)可知 s-c<0, 显然, 在式(6)的假设下, 当d12=d21=0时, 系统(3)的正平衡解E*是稳定的; 当d12和d21不同时为零时, 系统(3)的正平衡解E*的稳定性依赖于Dn的大小. 下面讨论交叉扩散对系统(3)的影响. 情形1: 当d12=0和d21≠0时, 由式(5)可知 c(s+e). 在这种情形中, 如果Dn>0, 那么E*是局部渐近稳定. Dn>0等价于 ∀n>0 (7) 由此可以发现, 如果d21<0, 式(7)显然成立, 从而E*是局部渐近稳定的. 从交叉扩散的生物意义得知, 如果捕食者向被捕食者密度高的方向运动, 并且被捕食者无目的运动, 那么E*是局部渐近稳定的. 如果d21>0并且至少存在一个n使 (8) 成立, 那么意味着如果d21>0和临界波长充分小使式(8)成立时, E*是不稳定的. 这种现象在自然界中的表现, 即为捕食者向被捕食者密度低的方向运动, 并且被捕食者无目的运动, 那么E*是不稳定的. 情形2: 当d12≠0和d21=0时, 由式(5)知 c(s+e). 在这种情形中, 如果Dn>0, 那么E*是局部渐近稳定的. Dn>0等价于 ∀n>0 (9) 由此可以发现, 如果d12>0, 式(9) 显然可以成立, 从而E*是局部渐近稳定的. 从交叉扩散的生物意义得知, 如果被捕食者向捕食者密度低的方向运动, 并且捕食者无目的运动, 那么E*是局部渐近稳定的. 如果d12<0并且至少存在一个n使 (10) 成立, 那么意味着如果d21<0和临界波长充分小使式(10)成立时, E*是不稳定的. 这种现象在自然界中的表现, 即为被捕食者向捕食者密度高的方向运动, 并且捕食者无目的运动, 那么E*是不稳定的. 情形3: 当d12≠0和d21≠0时, Tn和Dn如式(5)所示. 如果d12>0并且d21<0, 那么Dn>0成立, 从而E*是局部渐近稳定的. 如果d12>0, d21<0不成立, 就不能采用上述两种情形中的方法进行讨论. 下面讨论使E*不稳定的条件. 如果d11d22-d12d21<0, 那么必存在一些n可以使Dn<0, 这种情况是显而易见的. 当d11d22-d12d21>0, 假设在 (H1)(d11c-d12s+d12c+d21e)2+ 4(d11d22-d12d21)c(s+e)>0 成立的前提下, 如果 d11c-d22s+d12c+d21e<0 (11) 成立, 那么特征方程(4)的根有正实部. 不等式(11)等价于 (12) 显然, 如果式(12)中有一种情况成立, 那么E*是不稳定的. 根据式(12)可以得到下述定理. 定理1.1假设a, b, c, k1, k2>0, (H)和(H1)成立, 则若 当d12=d21=0时, 系统(3)的正平衡解E*是局部渐近稳定的; 当d12和d21不同时为零时, 系统(3)的正平衡解E*是图灵不稳定的. 图1描述了定理1.1的情形(Ⅰ). 选取扩散系数使其满足(Ⅰ)中所给的条件, 则有E*在图1中的区域M中是不稳定的. 类似地, 图2描述了定理1.1的情形(Ⅱ). 图1 定理1.1情形(Ⅰ)正平衡解E*图灵不稳定的区域MFig.1 The areaMwhere the equilibriumE*is Turing unstable of situation (Ⅰ) in Theorem 1.1 图2 定理1.1情形(Ⅱ)正平衡解E*图灵不稳定的区域MFig.2 The areaMwhere the equilibriumE*is Turing unstable of situation (Ⅱ) in Theorem 1.1 引理1.1假设a, b, c, k1, k2>0, d11=d12=d21=d22=0和(H)成立. 如果 (H2)ak1≥1 成立, 系统(2)的正平衡点E*是全局渐近稳定的. 定理1.2假设a, b, c, k1, k2>0, (H)和(H2)成立, 则若 (H3)(d12α+d21β)2 成立, 这里 证明令 (13) 当空间变量是二维时, 讨论正平衡点的全局稳定性. 类似定理1.2, 将给出二维情形下全局稳定性的定理. 定理2.1假设a, b, c, k1, k2>0, (H)和(H2)成立. 若(H3)成立, 系统(2)的正平衡点E*是全局渐近稳定的. 证明令 这里, W(U,V)在定理1.2的证明中已经给出定义. 将上式两边同时微分有 同理, 当(H3)成立时, 上式的第二个积分项和第三个积分项是大于零的. 同时, 当(H2)成立时,. 综上, 定理得证. 这里将通过数值模拟验证定理1.1. 由于文献[5]已经讨论过 d12=d21=1的情况, 所以将避免再取这样的数值, 从而能更清楚地看到交叉扩散系数取不同数值时系统(3)的解. 将一些参数固定, 并且令a和k2在图1和2的区域M中取值. 在图1中, 当(a,k2)∈M时, 正平衡点E*是图灵不稳定的, 将得到对应的解如图3所示. 由定理1.1可知,这里的图灵不稳定是仅由交叉扩散引起的, 当d12和d21重新赋值为0时, 正平衡点E*是稳定的, 将会得到稳定的解如图4所示. 同理, 令a和k2在图2中的区域M取值时, 也会得到相类似的结果, 如图5和6所示. (a)u(x,t) (b)v(x,t)图3 当扩散系数满足定理1.1情形(Ⅰ)时, 系统(3)的解Fig.3 The solution of the system (3) when the diffusion coefficients satisfying the situation Ⅰ of Theorem 1.1 图3中:d11=0.1,d22=0.2,d12=0.01,d21=0.24,k1=1,k2=0.8,a=0.35,b=1,c=0.25.(a,k2)=(0.35,0.8)属于图1的区域M, 此时正平衡解E*是不稳定的. 初值u(x, 0)=0.4-0.01cos(3x), v(x, 0)=1.2-0.01cos(4x). (a)u(x,t) (b)v(x,t)图4 当d12=0,d21=0时, 系统(3)的稳定的解Fig.4 The stable solution of the system (3) whend12=d21=0 图4中:d11=0.1,d22=0.2,d12=0,d21=0,k1=1,k2=0.8,a=0.35,b=1,c=0.25.(a,k2)=(0.35,0.8)属于图1的区域M, 此时正平衡解E*是稳定的. 初值u(x,0)=0.4-0.01cos(3x), v(x,0)=1.2-0.01cos(4x). (a)u(x,t) (b)v(x,t)图5 当扩散系数满足定理1.1情形(Ⅱ)时, 系统(3)的解Fig.5 The steady state solution of the system (3) when the diffusion coefficients satisfying the situation Ⅱ of Theorem 1.1 图5中:d11=0.1,d22=0.05,d12=-0.2,d21=0.2,k1=1,k2=0.2,a=0.15,b=1,c=0.25. (a,k2)=(0.15,0.2)属于图2区域M, 此时正平衡解E*是不稳定的. 初值u(x,0)=1.86-0.01cos(3x), v(x,0)=2.06-0.01cos(4x). (a)u(x,t) (b)v(x,t)图6 当d12=0,d21=0时, 系统(3)的稳定的解Fig.6 The stable solution of the system (3)whend12=0,d21=0 图6中:d11=0.1,d22=0.05,d12=0,d21=0,k1=1,k2=0.2,a=0.15,b=1,c=0.25. (a,k2)=(0.15,0.2)属于图2区域M, 此时正平衡解E*是稳定的. 初值u(x,0)=1.86-0.01cos(3x), v(x,0)=2.06-0.01cos(4x). 本文对同时带有自扩散和交叉扩散的捕食食饵模型进行了定性分析研究,重点关注交叉扩散对系统(2)稳定性的影响, 并分了3种情况进行分析. 与文献[4]相比, 本文得到了关于交叉扩散引起的图灵不稳定更一般的结论, 并给出了系统(2)和系统(3)全局稳定性的结论. 通过一些数值模拟验证理论结果,由数值模拟图可以清楚地看出正平衡点的图灵不稳定仅仅是由交叉扩散引起的. 事实上, 交叉扩散描述了捕食者和被捕食者有目的的运动, 所以当自扩散引起图灵不稳定时, 交叉扩散是否可以使系统重新获得稳定性, 这个课题有待于进一步的研究. [1] CAMARA B I, AZIZ-ALAOUI M A. Turing and Hopf patterns formation in a predator-prey model with Leslie-Gower-Type functional responses[J]. Dynamics of Continuous, Discrete and Impulsive Systems, 2009, 16(4): 478-488. [2] LI X, JIANG W H, SHI J P. Hopf bifurcation and Turing instability in the reaction-diffusion Holling-Tanner predator-prey model[J]. IMA Journal of Applied Mathematics, 2013, 78(2): 287-306. [3] UPADHYAY R K, THAKUR N K. Spatiotemporal pattern induced by self and cross-diffusion in a spatial Holling-Tanner model[J]. Computational Ecology and Software, 2012, 2(1): 1-25. [4] SUN G Q, ZHEN J, LIU Q X, et al. Pattern formation induced by cross-diffusion in a predator-prey system[J]. Chinese Physics B, 2008, 17(11):3936-3941. [5] PENG R, WANG M X. Stationary of the Holling-Tanner prey-predator model with diffusion and cross-diffusion[J]. Applied Mathematics and Computation, 2008, 196(2): 570-577. [6] TIMM U, OKUBO A. Diffusion-driven instability in a predator-prey system with time-varying diffusivities[J]. Journal of Mathematical Biology, 2013, 30(3): 307-320. [7] TIAN C R. Turing patterns created by cross-diffusion for a Holling Ⅱ and Leslie-Gower type three species food chain model[J]. Journal of Mathematical Chemistry, 2011, 49(6): 1128-1150. [8] WANG W M, GUO Z G, UPADHYAY R K, et al. Pattern formation in across-diffusive Holling-Tanner model[J]. Discrete Dynamics in Nature and Society, 2012: 1-12. [9] GOWDA K, RIECKE H, SILBER M. Transitions between patterned states in vegetation models for semi-arid ecosystems[J]. Nonlinear Sciences: Pattern Formation and Solitons, 2006,89(2): 1-9. [10] UPADHYAY R K, WANG W M. Spatiotemporal dynamics in a spatial plankton system[J]. Math Model Nat Phenom, 2010, 8(6): 1-21. [11] MARSDEN J E, SIROVICH L. Introduction to applied nonlinear dynamical systems and chaos[M]. New York: Springer-Verlag, 2003. Stability Analysis of a Predator-Prey Model with Cross-Diffusion LIUYang-yang (College of Science, Donghua University, Shanghai 201620, China) A predator-prey model incorporating the modified Leslie-Gower functional response is studied. The Routh-Hurwitz theory is applied to discuss the change of stability induced by cross-diffusion. The sufficient conditions for the stability of the nontrivial positive equilibrium is established. Then the corresponding theoretical results are verified by some numerical simulations. predator-prey model; Leslie-Gower functional response; cross-diffusion; stability 1671-0444(2015)03-0402-07 2014-04-21 国家自然科学基金资助项目(11101076) 刘阳阳(1989—),女, 黑龙江佳木斯人, 硕士研究生, 研究方向为偏微分方程. E-mail:pinyi_liu@163.com O 175.26 A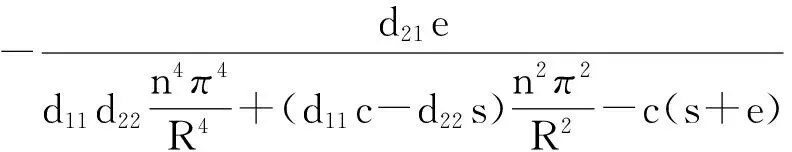
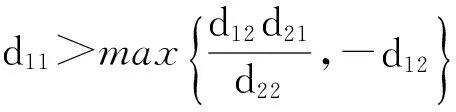

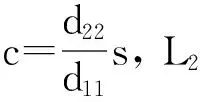


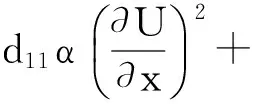
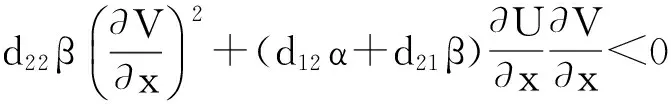
2 二维情形正平衡点稳定性分析
3 数值模拟





4 结 语

