基于K-Means和GA-WNN的交通流量预测
慕 伟, 陈国定, 钟引帆
(浙江工业大学 信息工程学院,浙江 杭州 310023)
基于K-Means和GA-WNN的交通流量预测
慕伟, 陈国定, 钟引帆
(浙江工业大学 信息工程学院,浙江 杭州 310023)
如何对交通流进行准确和实时的预测是实现交通管理的关键所在。文章根据交通流数据的时间序列特性,提出基于K-Means算法与遗传算法(GA)优化的小波神经网络(WNN)预测方法:首先对交通流流量序列按照流量采用K-Means算法进行分割,分割后的结果较符合流量的分布情况;然后使用GA-WNN对分割后的每一个时间段的交通流数据分别进行建模和预测。仿真结果表明,该方法对交通流量预测的精度较好。
交通流量预测;K-Means算法;遗传算法;小波神经网络
准确预测城市道路交通流量对交通控制和交通诱导起到非常关键的作用。交通流量预测是在实时的路段检测交通流数据基础上,将各种检测设备取得的实时数据通过适当的模型和方法利用历史数据预测得到下一时段流量的数据。目前,交通流的预测方法主要有自回归移动平均模型、时间序列模型、卡尔曼滤波模型、非参数回归模型、神经网络模型、支持向量机模型和组合模型等[1-10]。自回归移动平均模型方法计算简单,但不能反映出交通流过程的不确定性与非线性,无法应对突发事件对交通流造成的影响。时间序列模型方法较为成熟且预测精度较高,但初始化参数非常复杂、数据遗失严重。卡尔曼滤波模型方法是线性预测,所以在预测非线性的交通流数据时计算量较大,输出也有很大延迟。非参数回归模型方法通过历史数据中与当前点相似的“近邻”数据去预测下一时刻值,预测结果比参数建模精确[11-12]。支持向量机模型在解决小样本、高维非线性模式识别问题有优势。相比之下神经网络模型更适合复杂、非线性的交通流预测。神经网络模型中在非线性参数估计和逼近中应用较好的是小波神经网络(WNN),相对于BP神经网络,WNN时效性和收敛性方面都有明显改善。遗传算法(GA)是一种自适应全局优化的概率搜索算法,具有内在的隐并行性和更好的全局寻优能力;概率化的寻优方法能够自动获取和指导优化的搜索空间,自适应地调整搜索方向。用GA优化WNN可以使其具有较快的收敛性和较强的学习能力[13]。
本文采用GA-WNN的预测方法,同时考虑了交通流时间序列的特性,提出了对交通流数据使用K-Means算法进行分割后再进行分段预测的方法。
1 交通流量的序列分割
1.1 K-Means算法简介
K-Means算法是由MacQueen在1967年提出的,作为较早期的聚类分析算法之一,它在很多学科领域中都有着广泛的应用[14]。它是基于目标函数的聚类分析方法,目的是将样本聚类成K个簇,其算法步骤有以下4个步骤:
(1)初始化。已知m个数据点的集合X={x1,x2,…,xi,…,xm},其中xi∈R以及K个初始聚类集合C={c1,c2,…,cK},每个划分是一个类cK,每个类都有一个聚类质心点μi。以欧氏距离作为判断准则,计算每类样本点到质心μi的距离平方和。
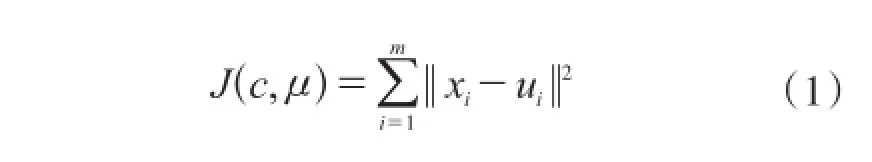
(2)样本分类。对于样品中的数据点,根据它们与聚类质心点的距离,以距离最近即J(c,μ)最小的准则分别将它们分配给与其最相似的聚类质心所代表的类。
(3)计算新的聚类质心C*。计算每个类别中所有数据点的均值作为该类的新聚类质心。

式中:Ni是ck中的样本个数。
(4)检验是否收敛:重复迭代第2步和第3步直到质心不变或者变化很小,算法停止[10]。
1.2 交通流量的聚类分析
选取K-Means算法作为交通流量序列分割的方法,对一天或者一周甚至更长时间的交通流量作为聚类的原始样本数据点。由于交通流量数据呈现一定的规律性,每一天从00∶00~24∶00的流量变化趋势非常相似,所以采用预测当天前一周同一天的流量数据来进行聚类分析,流量聚类分析的步骤如下:
(1)首先对于交通流量样本X根据流量值的大小,采用欧氏距离作为目标函数,取K=3将其聚为类C1、C2、C3,流量值依次递减。
(2)根据时间的先后顺序将C1分为2类,而C2分为3类,C3分成2类,之所以这样聚类是由于交通流量变化呈双峰状。
(3)最终一天的交通流量聚类分割之后变为7类,类与类之间可以通过时间的先后顺序分辨出来。
2 交通流量预测模型
本文采用GA-WNN为交通流预测模型,小波神经网络是小波理论与人工神经网络的结合,用非线性小波基函数取代了BP神经网络原有的非线性传递函数,结合了小波变换的时频局域化较好的特点以及BP神经网络的自学习能力,预测效果要优于BP神经网络[15]。
2.1 小波神经网络的拓扑结构
小波神经网络预测模型结构与传统的BP神经网络一样采用3层结构,即输入层、隐含层、输出层。本文采用示。
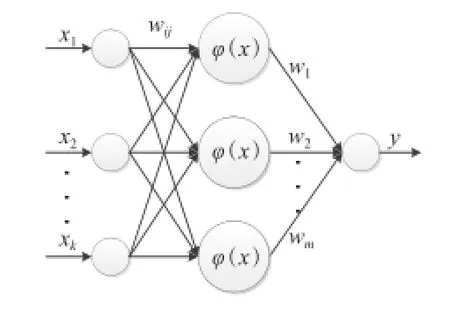
图1 小波神经网络拓扑结构
图中x1,x2,…,xk为网络输入参数,k为输入层结点个数,m为隐含层结点个数,wij为输入层结点i(i=1,2,…,k)跟隐含层结点j(j=1,2,…,m)连接的网络连接权值,w1,w2,…,wm为隐含层跟输出层之间的网络连接权值,y为网络输出层的输出值。
根据交通流量的相关性,构造小波神经网络交通流预测模型。其中某路段交通流量Qt与其前几个时段的交通流量有必然联系,本文输入层有4个神经元(Qt, Qt-1,Qt-2,Qt-3);隐含层神经元个数的确定一直是神经网络的领域的难点,我这里采用传统的经验测试法,一般取2k+1;输出结点数为1,即预测的交通流量Qt+1。
隐含层转移函数φ(x)选取的是小波函数Morlet,其定义如下:

对φ(x)做伸缩和平移变换便可以得到小波基函数φa,b(x):

式中:a为伸缩因子,b为平移因子。
输出层激励函数采用Sigmoid函数:
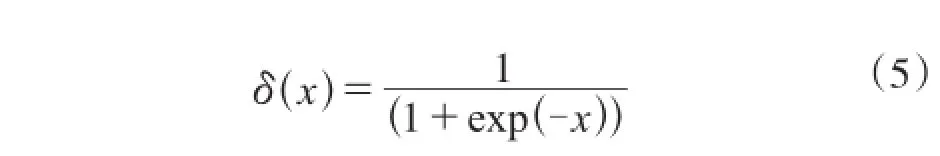
网络输出y为:
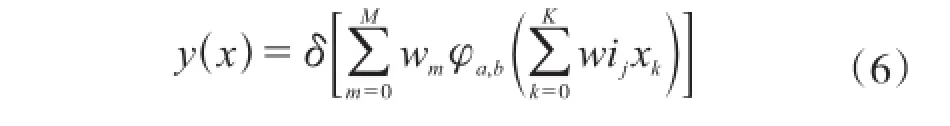
2.2算法流程
本文根据交通流量数据时变、非线性的特点,设计了小波神经网络,其具体算法流程如图2所示。
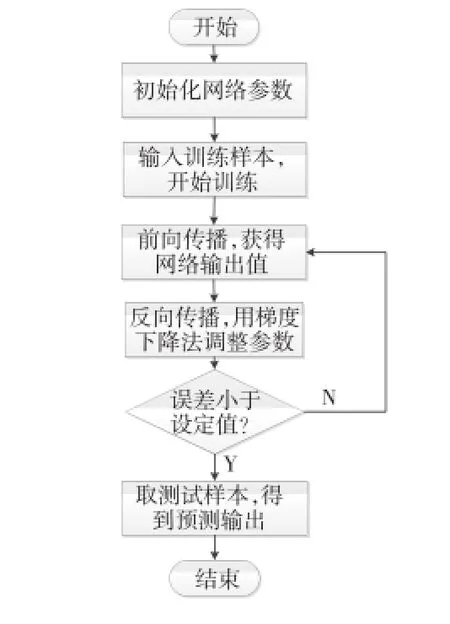
图2 小波神经网络算法流程
当输入交通流量样本数据时,小波神经网络首先进行前向传播得到网络的输出值,然后根据输出值与期望值之间的误差反向传播调整连接权值等参数。小波神经网络的反向传播采用梯度下降法修正权值参数,其修正过程为:式中:yqw为期望输出;y为预测输出。
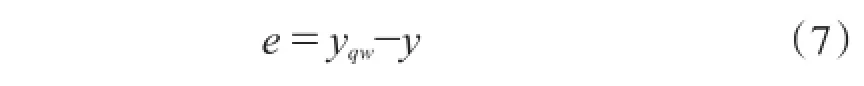
取均方误差函数E为性能指标函数,其表达式如下:
为了使误差E最小,采用梯度下降法修正网络参数:

式中:wij和wm为网络权值;aj为伸缩因子;bj为平移因子。
可以看出参数修正方法都是一致的,修正的过程可以反映出误差反传播的思想。但是单一的采用梯度下降法来优化参数,整个网络容易陷入局部极小和引起振荡效应,因此在WNN的基础之上,利用遗传算法对其参数进行优化来提高预测精度。
2.3 基于遗传算法的小波神经网络参数优化
遗传算法是基于自然选择和遗传学的优化搜索算法。对小波神经网络连接权值和平移伸缩因子参数进行编码,形成染色体并对其进行复制、交叉及变异操作,染色体不断进化,从而产生最优解的染色体,即网络的参数。参数优化步骤如下:
(1)选择编码方式
设初始种群规模为N,对种群规模N,网络连接权值wij和wm、伸缩因子aj和平移因子bj进行初始化编码。采用实数进行编码,交叉概率为Pc,突变概率为Pm,解码时将基因值作为网络相应的参数。
(2)确定个体适应度函数
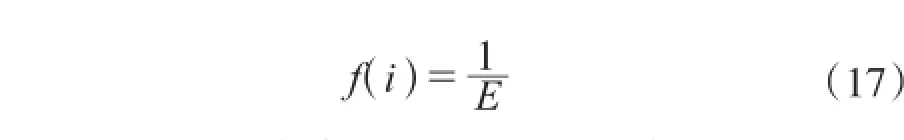
个体i的适应度函数f(i)为:式中:E为上述小波神经网络的误差函数。
(3)选择算子
每一个个体按照其适应值进行排序,采用轮盘赌选择法,然后按照公式(18)选择网络个体:
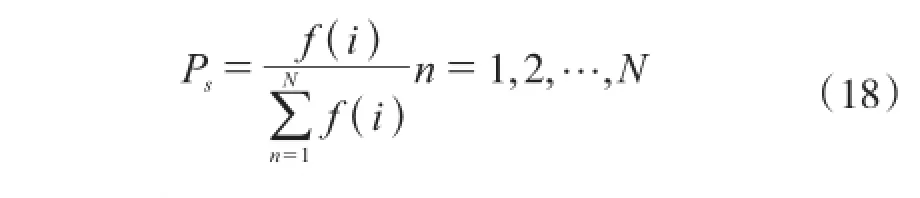
(4)交叉变异
以概率Pc对2个个体Ga和Gb进行交叉运算后产生的2个新个体G'a和G'b,没进行交叉运算的其他个体直接进行复制即可。以概率Pm采用均匀变异法进行变异操作产生新的个体,并将新个体插入到种群P中,并计算新个体的适应度,如果适应度满足精度要求,优化过程结束。将最终的群体中最优个体解码作为小波神经网络的连接权值和伸缩平移因子。再通过对样本训练,最终得到经遗传算法优化的小波神经网络预测输出。
3 仿真试验
本文以杭州市天目山路段为研究对象,根据该路段实测的交通流量历史数据(连续4天工作日凌晨0∶00到晚上24∶00,每15 min一组的交通流量数据),共整理得到368条数据,取前3天的276条数据作为训练样本,最后一天的92条数据作为测试样本。
未分段只采用小波神经网络进行预测,网络结构为4-9-1,即输入层参数为4个过去时间点的流量(Qt,Qt-1,Qt-2,Qt-3),隐含层为9个,输出层为1个预测
输出交通流量Qt+1,为了方便比较,本文采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方误差(MSE)、均方百分比误差(MSP)作为模型的评价指标,预测的交通流量图和实际的交通流量图如图3所示:
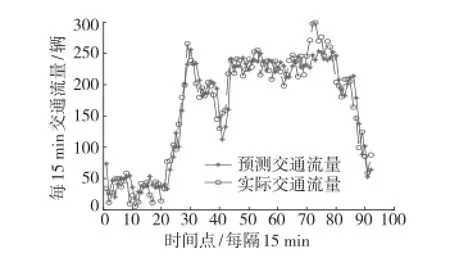
图3 小波神经网络预测交通流量
模型的指标预测误差如表1所示。

表1 未分段的小波神经网络预测误差
采用本文的方法预测,首先使用K-Means算法对交通流序列进行划分,样本数据为预测当天前一周同一天的从凌晨0∶00到晚上24∶00的交通流量历史数据,根据1.2小节的划分步骤将一天的交通序列划分为0∶00~5∶45,5∶45~7∶00,7∶00~9∶45, 9∶45~15∶15,15∶15~18∶30,18∶30~22∶15,22∶15~23∶45共7个时间段,如图4所示。
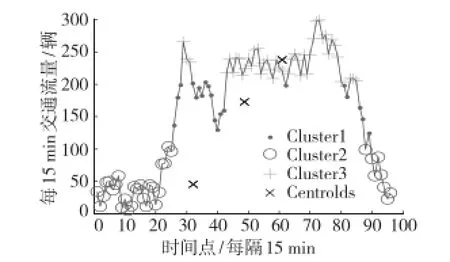
图4 交通流量时间序列聚类图
而实际上22∶15~23∶45与0∶00~5∶45为连续的时间段且聚类结果为同一类,所以预测时把2个时间段归为一个时间段进行预测。然后对交通序列分割之后的每个时段分别用小波神经网络预测模型进行预测,得到各时段的预测误差如表2所示。
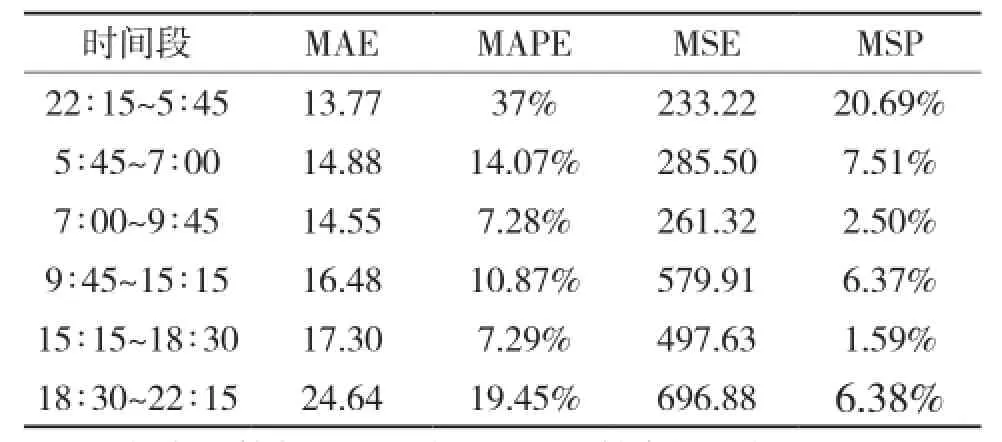
表2 各时段的预测误差
由表2数据可以看出,流量较低的时段预测误差相对较高,流量较高的2个高峰时段预测误差相对较低,后5个时段的预测误差都要小于未采用序列分割的小波神经网络预测模型。
对于分割后的交通流量序列采用遗传算法优化小波神经网络参数时,种群规模取10,交叉概率取0.4,变异概率为0.2,遗传代数为100,网络的目标误差为0.01,网络结构为4-9-1。以下是流量较高的2个高峰时段分别采用WNN、GA-WNN的预测结果,并给出了未分段前采用WNN的预测结果。
第1个交通流量的高峰时段为7:00~9:45,预测结果和实际交通流量对比如图5所示,第2个高峰时段在15∶15~18∶30,预测结果和实际交通流量对比如图6所示。
由表1和表2可以得出,分段后的预测结果优于未分段前的预测结果,但是预测精度并没有很大的提升。由图5和图6可以得出,采用遗传算法改进的小波神经网络预测精度相比于小波神经网络有较大的提升,可以更好地预测交通流量。
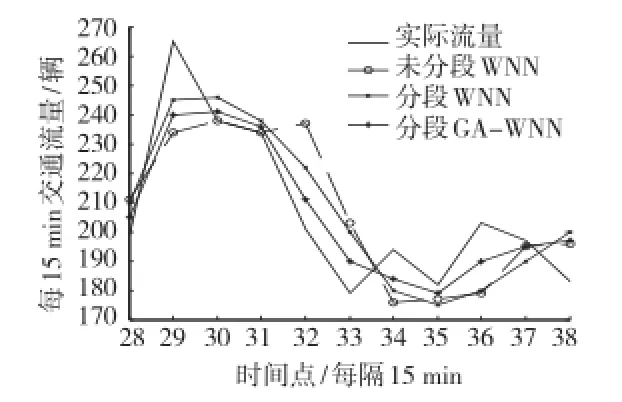
图5 第1个高峰时段的预测结果图
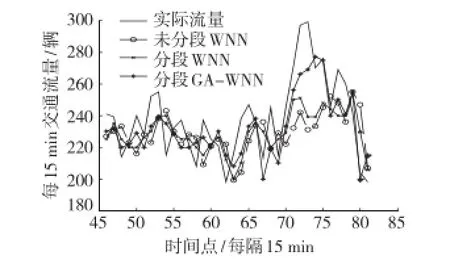
图6 第2个高峰时段的预测结果图
4 结论
本文针对交通流量序列的特性,提出了K-Means和GA-WNN结合的预测方法。首先对一天的交通流量序列采用K-Means算法进行聚类,将其划分成7个时间段,然后再分别对每一个时间段采用遗传算法优化的小波神经网络预测模型进行预测。仿真结果表明,分段后的预测精度高于未分段,经GA优化WNN模型的收敛速度较WNN更快,预测精度也更高,可以有效地预测下一时段的交通流量。
[1]史其信,郑为中.道路网短期交通流预测方法比较[J].交通运输工程学报,2004,4(4):68-71.
[2]韩超,宋苏,王成红.基于ARIMA模型的短时交通流实时自适应预测[J].系统仿真学报,2004,16(7):1530-1535.
[3]臧利林,贾磊,杨立才,等.交通流实时预测的混沌时间序列模型[J].中国公路学报,2007,20(6):95-99.
[4]Xie Yuanchang,Zhang Yunlong, Ye Zhirui. Short-term traffic volume forecasting using Kalman filter with discrete wavelet decomposition[J].Computer-Aided Civil and Infrastructure Engineering,2007,22(5):326-334.
[5]杨兆升,朱中.基于卡尔曼滤波理论的交通流量实时预测模型[J].中国公路学报,1999,7(3):63-67.
[6]宫晓燕,汤淑明.基于非参数回归的短时交通流量预测与事件监测综合算法[J].中国公路学报,2003,16(1):82-86.
[7]傅惠,胡刚,徐建闽,等.基于神经网络的城市关联交叉口交通流预测控制方法[J].中国公路学报,2008,21(5):91-95.
[8]傅贵,韩国强,逯峰,等.基于支持向量机回归的短时交通流预测模型[J].华南理工大学学报,2013,41(9):71-76.
[9]杨显立, 许伦辉, 周勇.基于小波神经网络的道路交通流>量实时预测模型研究[J].公路交通技术,2013(5):111-113.
[10]沈国江,王啸虎,孔祥杰.短时交通流量智能组合预测模型及应用[J].系统工程理论与实践,2011,31(3):561-568.
[11]Smith BL,Williams BM,Oswald RK. Comparison of parametric and nonparametric models for traffic flow forecasting[J]. Transportation Research Part C-Emerging Technologies,2002,10(4):303-321.
[12]张晓利,陆化普.非参数回归方法在短时交通流预测中的应用[J].清华大学学报,2009,49(9):1471-1475.
[13]杨超,王志伟.经GA优化的WNN在交通流预测中的应用[J].计算机工程,2011,37(14):149-151.
[14]王千,王成,等.K-means聚类算法研究综述[J].电子设计工程,2012,20(7):21-24.
[15]陈振伟,郭拯危.小波神经网络预测模型的仿真实现[J].计算机仿真,2008,25(6):147-150.
Traffic Flow Prediction Based on K-Means and GA-WNN
Mu Wei, Chen Guoding, Zhong Yinfan
(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)
Accurate and real-time traffic flow prediction is the key to the implementation of traffic management. According to the characteristic of time series of traffic flow, a prediction method based on K-Means and wavelet neural network (WNN) optimized by genetic algorithm (GA) is proposed. Firstly, traffic flow sequence is segmented according to the flow using the K-Means algorithm, the segmented results is in agreement with the distribution of flow; and then the GA-WNN method is used for modeling and forecasting of the segmented traffic flow data respectively. The simulation results show that the traffic flow prediction accuracy of the method is better.
traffic flow prediction; K-Means algorithm; genetic algorithm; wavelet neural networks
U491.1+12
A
1672–9889(2015)05–0070–05
慕伟(1991-),男,安徽亳州人,硕士研究生,研究方向为智能交通。
(2015-01-08)

