基于改进型Dijkstra算法的模块机器人系统故障自诊断策略
管恩广, 付 庄, 闫维新, 赵言正
(上海交通大学 机器人研究所, 上海 200240)
基于改进型Dijkstra算法的模块机器人系统故障自诊断策略
管恩广, 付庄, 闫维新, 赵言正
(上海交通大学 机器人研究所, 上海 200240)
面向模块机器人系统,提出了一种全新的故障自诊断策略.该策略将故障自诊断过程分为两个部分:故障检测及故障消息传递.选用健康脉冲法实现模块间的交互式故障检测.设计优化改进型Dijkstra距离计算方法,并依据这种方法引导故障消息在模块间沿最优路径传递.通过仿真试验,该自诊断策略的有效性和可靠性在M-Lattice模块机器人系统上得到了验证,表明该策略可以广泛应用于其他模块机器人系统.
模块机器人系统; 故障自诊断; M-Lattice模块机器人
在模块机器人系统中,故障的发生是不可避免的.当故障发生时,能否以最快速度发现并定位故障对于保证系统正常工作是至关重要的.模块机器人系统的自诊断策略设计很大程度上受系统结构影响.模块机器人按结构可以分为3个类别:晶格式、链式和综合式.晶格式模块机器人系统结构一般为网格状,如CHOBIE[1]和ATRON[2].链式模块机器人系统结构一般为线形或树形,如YaMor[3].综合式模块机器人可以同时完成晶格式和链式构型,如Roombots[4]、iMobot[5]和 UBot[6],由于该系统具有灵活的构型模式,其诊断策略设计难度也比前两者大.
目前已有相关文献介绍针对精密机器人个体的故障诊断方法[7],但是对于模块机器人系统的诊断策略研究并不多见.大多数对群体机器人系统的故障诊断研究集中于自主移动式群体机器人.在一些机器人系统中,系统状态包括通信负载、故障定位等,通过图的方式进行表达分析[8].在图理论(graph theory)中,以节点(vertex)表示机器人个体,边(edge)表示机器人间的物理或者通信连接关系.基于故障概率模型的诊断方法[9-10]在某些自主移动机器人群体中被证明是有效的,但是模块机器人个体并不具备自主移动能力,所以这类方法很难应用于模块机器人系统.超预期学习[11](surprise-based learning, SBL),是目前面向模块机器人系统容错性设计最系统的指导理论,但其使用过程中需要不断地进行全局训练以优化故障对策,且算法本身非常复杂,因而无法作为离散的控制策略应用于M-Lattice模块机器人系统中.
为解决大规模模块机器人系统的故障诊断问题,本文提出了一种故障自诊断策略.这种自诊断策略原理简单,可以独立运行于模块机器人个体,仅通过模块间的局部通信,就可以完成故障诊断.该自诊断策略主要由以下两个部分组成:
(1) 故障检测.选择健康脉冲信号法作为交互式故障检测方法.在模块机器人系统中,每个模块均以探测者的身份检测与之相连接的模块是否能够周期性地发出健康信号.若没有接收到某一邻位模块的健康信号,则认为该邻位模块为故障模块,并生成一条包含故障位置坐标的故障消息.
(2) 故障消息传递.在模块机器人系统中,模块个体可以通过局部通信将故障消息传递给与其连接的邻位模块.为了保证仅在局部通信的情况下,故障消息能够沿最优路径传递到系统消息接收端,提出了一种改进型离散Dijkstra算法,用以适应由故障模块出现导致的最优路径变化.
为了验证本文自诊断策略的有效性和可靠性,选择M-Lattice模块机器人系统作为验证平台,其是一种可以实现二维空间自构型的晶格式模块机器人.M-Lattice模块相互连接可以形成网格状平面.在验证自诊断策略时,假设故障模块不会脱离系统,即故障模块群体至少与一个正常模块相连接.
1 M-Lattice模块机器人系统
M-Lattice机器人[12]是一种非紧密式的晶格式模块机器人,如图1所示.由图1可知,每个模块包含一个中心框体和三条两自由度机械臂,并且每个模块最多可以同时与3个模块保持连接.作为分布式模块机器人系统,每个机器人个体只能以局部通信的方式与邻位模块进行通信.
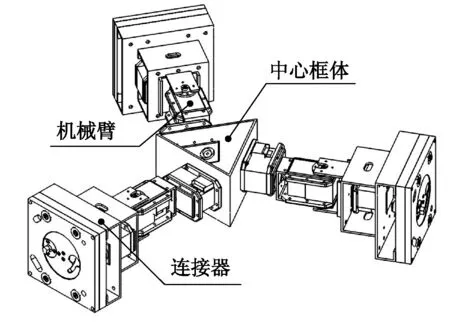
(a) 模块结构图

(b) 模块实物图
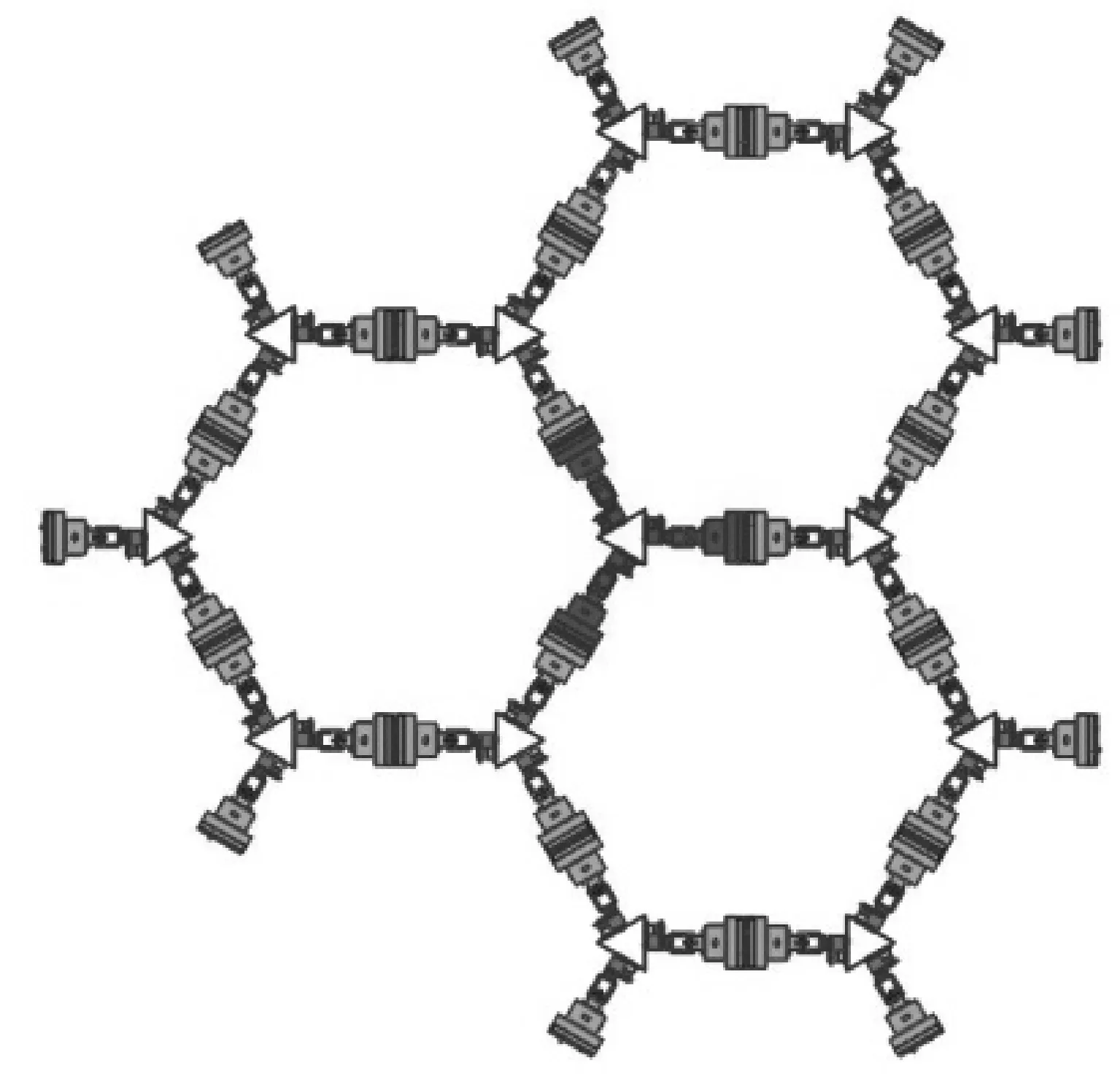
(c) 模块连接图图1 M-Lattice模块机器人Fig.1 The M-Lattice modular robot
M-Lattice的系统结构为网格状平面结构.在描述模块在系统中的位置时,使用一种有序整数对的索引位置来表示,其形式为(r,c),r表示模块所在的行数,c表示模块所在的列数,如图2所示.模块在系统中的索引位置和实际位置可以由简单的几何变换得到.
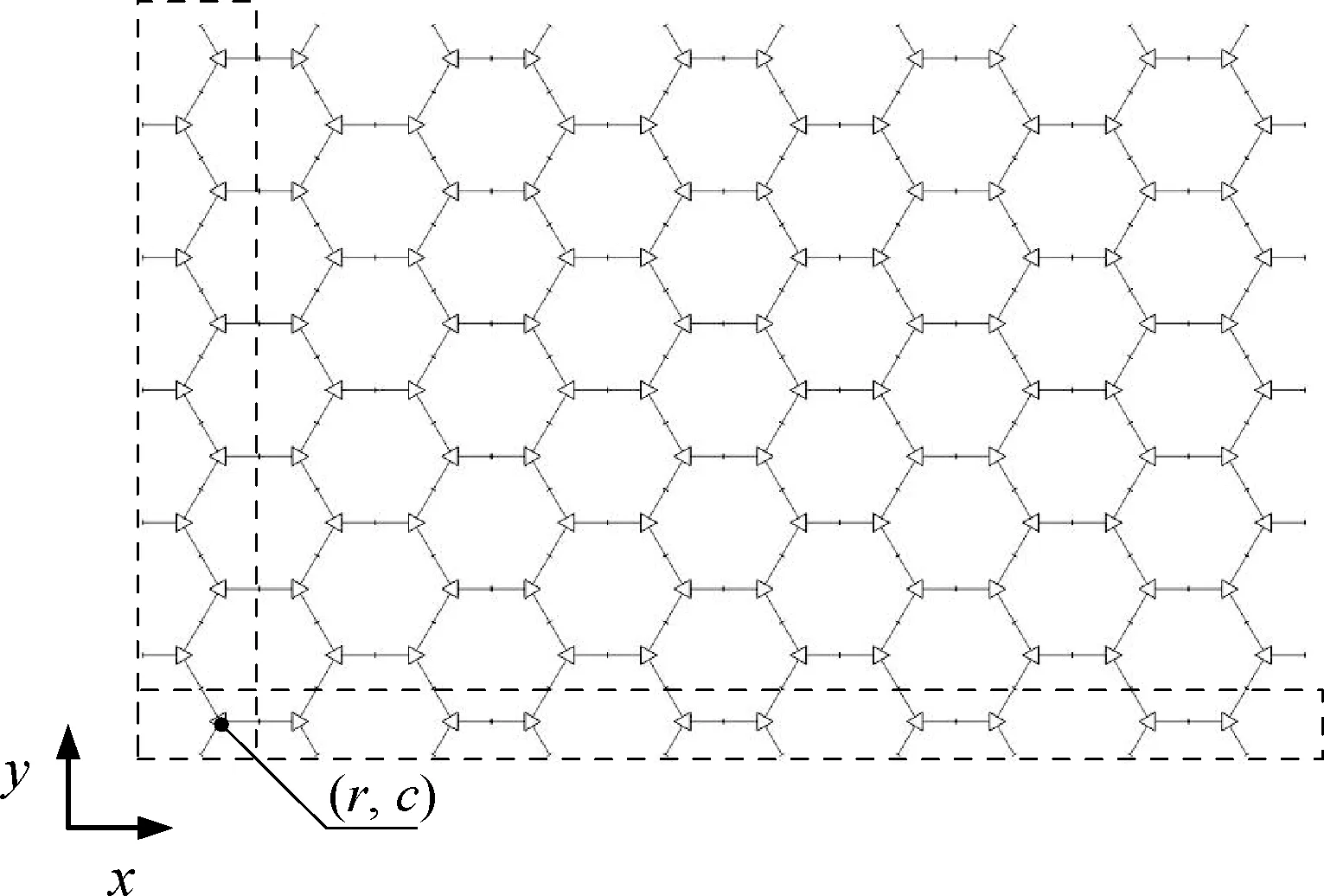
图2 M-Lattice系统拓扑结构Fig.2 The topology structure of the M-Lattice system
2 故障自诊断策略
在M-Lattice系统中,模块按工作状态可分为故障模块和正常模块.当正常模块检测到其邻位模块故障时,会自动生成一条故障信息,并将其发送给邻位正常模块.该消息可以在系统中通过局部通信传输,直至被系统监测器收到,完成一个故障模块的诊断过程.
2.1故障检测
由于精密机器人个体的自身故障检测方法很难直接应用于运算能力有限的模块机器人,所以选择健康脉冲法来实现模块间的故障交互检测.通过预先设定,使得每一个模块在工作正常时都可以定时发送一个类似心跳的脉冲信号,称为健康脉冲.这个信号通过模块间的连接通道发送给邻位模块.当模块功能部分不可控时,例如运动执行机构无反应,或者传感器响应异常时,通过内部有限状态机的方式便可以停止脉冲定时发送.当模块遇到意外碰撞或者系统掉电时,模块完全失效,也将无法继续发送脉冲信号.健康脉冲信号法如图3所示,可以通过检测邻位模块是否定时发出脉冲的方式检测该模块是否发生故障.判断准则:若一个正常模块在自己发送两次健康信号之间接收到邻位模块的健康脉冲,则认为该邻位模块正常;反之,则认为检测到一个故障.

图3 健康脉冲信号法示意图Fig.3 An illustration of the healthy pulse method
2.2故障消息传递
当一个故障模块被检测到,其邻位的正常模块将生成一条包含故障位置的故障消息,并将其在系统中传递.故障消息通过局部通信的方式在正常模块间传递,最终到达系统监测器位置,也称为消息收集器.在故障消息传递的路径规划方面,最重要的问题在于如何找到一种适用于离散模块机器人系统的路径长度表示方式.这种方法能够直观地反映系统的状态变化,并且能够直接被模块机器人个体执行.为此本文设计了一种改进型离散Dijkstra算法来计算模块机器人系统中的路径长度.
2.2.1消息传递路径描述
M-Lattice系统网络可以用一种无向图的方式表示,记为G=(V,E,w),其中,V表示模块机器人集合,E表示模块间的连接状态,w表示连接关系权重.边的表达方式为无序对(m1,m2),其中m1和m2为相邻模块.在传统的图理论中,u和v两点间的路径可记为一个有限序列:
p = {u≡ v0, v1, …, vk≡ v},
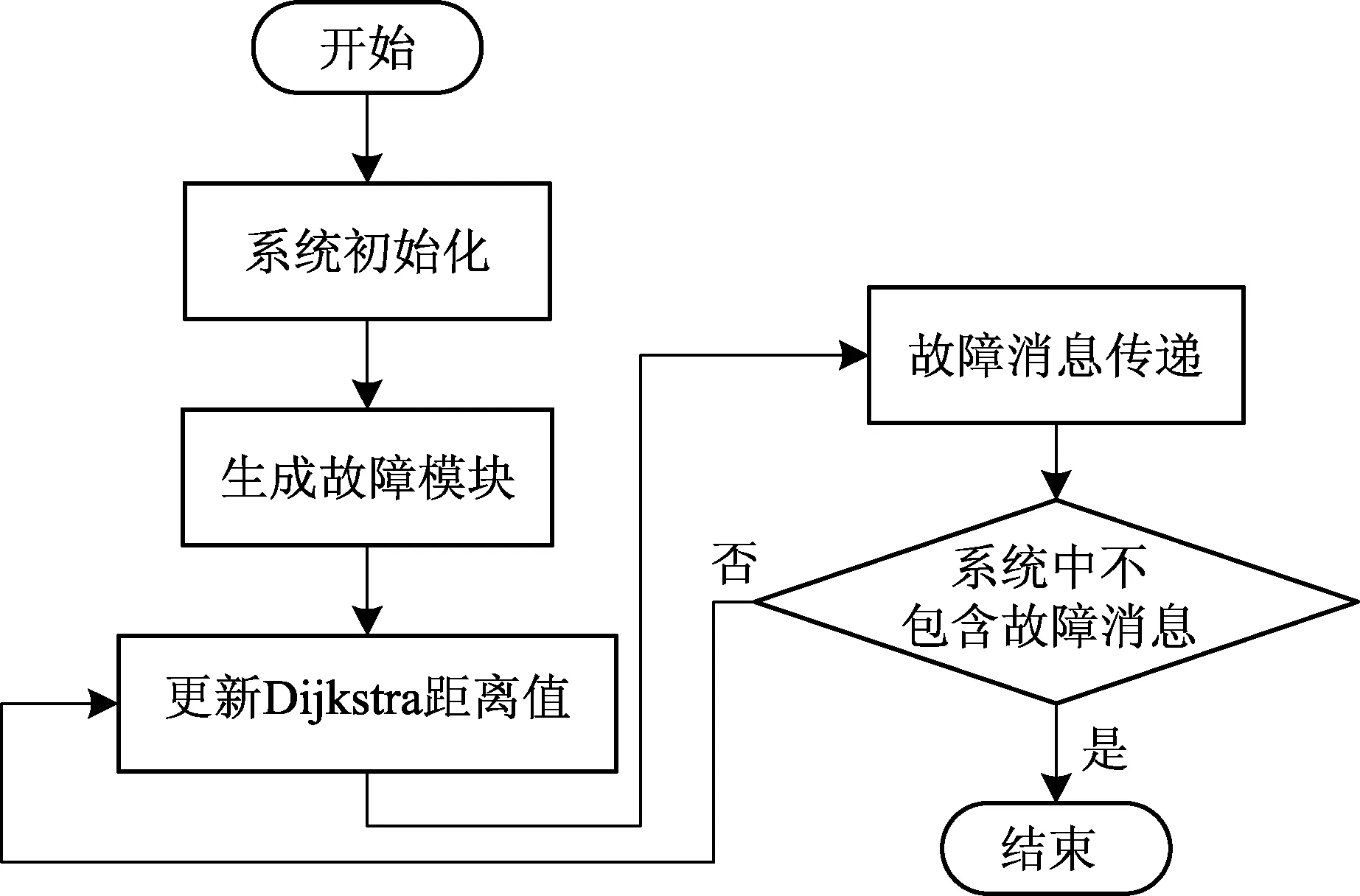
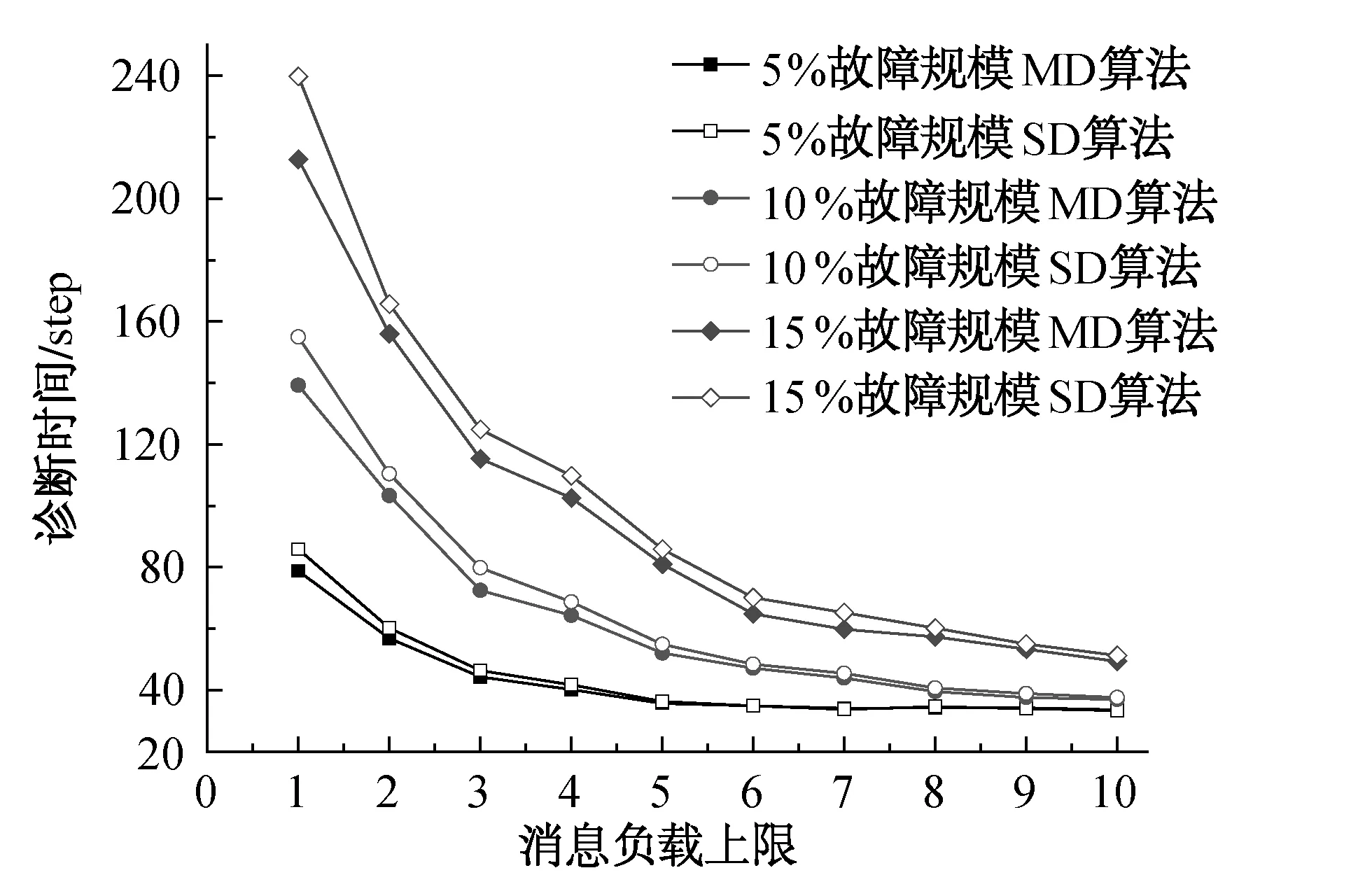
满足0≤i 整个路径的权重为 此所谓的寻找最短路径的问题就转化为寻找u和v之间所有路径中权重之和最小的那一条路径.在M-Lattice系统中,由于没有全局广播通道,模块间只能够进行局部通信.对于模块u而言,它和目标模块v之间的路径就变为 p = {u, v0≡v1, v2, …, vk≡v},满足0≤i 在这种情况下,u与v之间路径权重也变为 如果规定任意相邻模块间的权重值都相同,那么最短路径必定包含一个具有最小权重之和的邻位模块. 2.2.2改进型离散Dijkstra算法 在上述内容的基础上,选用离散Dijkstra算法来计算系统的路径长度.在Dijkstra算法[13]中,当前模块和目标模块间最短路径所包含的模块个数称为Dijkstra距离,记作D.系统中的每一个模块都可以保存并更新当前的Dijkstra距离.Dijkstra距离示意如图4所示,规定消息收集器的位置为系统目标模块所在位置,即D=0,这样其邻位模块的Dijkstra距离记为D=1,并以此类推.在消息传递过程中,只需要保证将消息传递给Dijkstra 距离最小的那个模块,则可以保证消息传递路径最优. 图4 Dijkstra距离示意图Fig.4 Some illustrations of Dijkstra distance 模块个体更新自身Dijkstra距离值依照的规则如下: (1) 当连接状态发生变化时,模块触发更新Dijkstra距离值操作,并向所有邻位模块发送读取其Dijkstra距离值的请求; (2) 读取邻位Dijkstra距离值过程中,若邻位为空位或故障模块,则其Dijkstra距离值视为无穷大,记作INTMAX; (3) 选择所有邻位Dijkstra距离值中最小的一个,记为Df,则更新自身Dijkstra距离值为Df+1. 在实际应用Dijkstra算法过程中,为避免过多的消息同时传送给一个模块,引发消息过载,给出了一个广义距离函数对Dijkstra距离值进行处理.这种处理后的Dijkstra距离值被称为改进型Dijkstra距离值,记为MD(Modified Dijkstra)距离.与其相对应的,之前介绍的Dijkstra距离值称为标准Dijkstra距离值,记为SD(Standard Dijkstra )距离.广义距离函数形式为 (1) 其中:D*为当前模块的MD距离值;D为当前模块的SD距离值;M为模块的最大消息负载上限;L为当前消息负载;α为功能因子,后续试验中设为0.2.当模块已经接收到大量的故障消息时,其返回的MD距离值会增大,这样新的消息将不会继续传递给这个模块. 本文使用Matlab软件对故障诊断策略进行仿真,其工作平台为CPU Pentium E5200 Dual-Core, RAM 2 GB.在仿真过程中,模块机器人系统以无向图的方式表达,即G=(V,E,w),其中连接关系权重值w以相邻模块间的Dijkstra距离值表示.系统网格形状定义为矩形,模块规模为m×n,其中,m为行数,n为列数.系统中的消息收集器可被安置于任意位置.依据Dijkstra算法,模块更新Dijkstra距离值.在仿真开始前初始化阶段中,设定系统规模、故障模块规模、消息收集器数量及位置以及模块消息负载上限.仿真开始后,依据故障规模随机选择模块将其设定为故障模块,这时系统中模块将更新Dijkstra距离值.当正常模块检测到邻位模块为故障模块后,将生成一条包含故障位置的故障消息,并将其发送给拥有最小Dijkstra距离值的正常邻位模块.故障诊断流程如图5所示.在仿真过程中,故障消息的传递路径由仿真程序独立保存.如果系统中没有消息进行传递,则认为一个仿真试验完成. 图5 故障诊断流程图Fig.5 Flow diagram of fault diagnosis 3.1系统扩展性测试 首先测试诊断策略的系统扩展性.试验中,系统规模由100×100变化至200×200,消息收集器个数为1, 2和4,消息收集器的位置对称分布于矩形平面的4个顶点,以减少相互间影响,故障模块数量为系统模块数量的1%,模块个体的消息负载上限为无穷大.每个状态下规模重复试验30次. 变系统规模情况故障诊断仿真结果如图6所示.图6中平面内点表示故障模块所在位置,其位置表示方式已经转换为笛卡尔坐标,而不是索引坐标,这样更能直观地表示故障位置与消息传输路径的关系.柱状图给出了路径的长度.由于故障规模比较小,所以相互间影响有限,因而将相同规模的试验数据取平均后,在同一个图里表示出来.从图6(a)和6(b) 中可以看出,在故障规模较小的情况下,故障消息的路径长度基本正比于故障模块位置与消息收集器间的距离.由图6(c)和6(d)可知,消息收集器的增加显著缩短了故障消息的传输路径长度,即提高了诊断效率.这是由于在M-Lattice系统中,多个Dijkstra距离为0的消息收集器的引入,缩短了系统的平均Dijkstra距离值.由于多个消息收集器的存在,消息可以被传递给最近的消息收集器,而不必再穿过整个系统,这样提高了消息传递的并行性,即提高了消息传输效率. (a) 10000个模块1个消息收集器 (b) 40000个模块1个消息收集器 (c) 10000个模块2个消息收集器 (d) 10000个模块4个消息收集器图6 变系统规模情况的故障诊断Fig.6 Fault diagnosis with different system scales 3.2消息负载上限的影响 真实的模块机器人个体不可能具有无限的消息负载能力,所以模块负载能力对诊断效率的影响不能被忽略.在消息负载上限的影响试验中,系统规模为50×50,消息收集器数量分别为1和4;故障规模分别为系统规模的5%, 10%和15%;消息负载(最大接收消息数量)上限范围为1~10.同等情况下重复试验10次.在每一组试验中,系统分别使用SD算法和MD算法计算Dijkstra距离值.消息在模块间的连续传递离散化为一系列的传递单元.在每个仿真周期(step)内,消息只从一个模块传递到另一个模块.若当前模块接收到的消息已经达到最大负载上限,则不能再接收消息. 变消息负载上限的故障自诊断仿真结果如图7所示,其中诊断时间以消息传递的步数表示,每一步表示系统中的故障消息由当前模块传递给邻位模块.由图7可知,增加模块消息负载上限对于整体诊断效率的提高并不是无限的.由于故障模块发生位置上的差异,必定导致其故障消息传输到消息收集器的时间存在差异,这就降低了模块发生消息过载的几率.与此同时,提高模块的消息负载上限会导致模块个体成本的上升,这对于大规模系统也是不能忽略的.由图7还可以发现,在同等故障条件下,MD算法要优于SD算法.这主要是由于MD算法将当前模块的消息负载情况作为一个前馈值引入到Dijkstra距离值计算中,避免了消息过载发生的概率,也就提高了系统的诊断效率.另外,系统消息收集器的数量改变只影响整体的诊断效率,并不改变模块消息负载上限和系统故障规模之间的对应关系.也就是说,为了提高诊断效率,考虑以增加消息收集器的方法更为有效. (a) 1个消息收集器 (b) 4个消息收集器图7 变消息负载上限情况的故障诊断Fig.7 Fault diagnosis with changeable message load capacity 在测试故障自诊断策略在大规模M-Lattice模块机器人系统中的表现时,系统规模为100×100,故障规模分别为系统规模的5%, 10%和15%,消息收集器数量分别为1和4,模块个体最大消息负载上限为6条消息.在每组试验中分别使用MD算法和SD算法计算Dijkstra距离值.每种情况重复试验30次,试验结果如表1所示.由表1可以看到,在大故障规模下MD算法在诊断效率上较SD算法表现更为突出.同时,在中等规模的故障系统中,自诊断策略都有非常高的直接诊断成功率,而且增加消息收集器可以非常明显地提高系统诊断效率. 表1 故障自诊断策略仿真结果Table 1 Simulation results of the self-diagnosis strategy 本文介绍了一种针对模块机器人系统的故障自诊断策略,并通过M-Lattice模块机器人系统对该策略的有效性和可靠性进行了仿真验证.整个故障诊断任务基于局部通信完成,不需要全局广播.模块间使用交互式健康脉冲法进行故障检测,可以保证同一个故障模块可以同时被多个邻位模块检测到,进而提高了故障检测环节的可靠性.在故障消息传递过程中,通过使用改进型Dijkstra算法,确保故障消息在模块机器人系统中始终沿最优路径进行传递,有效提高了诊断效率.通过仿真试验可以证明,该故障自诊断策略对于大规模模块机器人系统是有效可靠的.在今后的工作中,计划继续改进故障自诊断策略,以适应在复杂故障类型下的模块机器人自诊断任务,同时,在自构型和自修复任务中,如何发挥自诊断策略的作用也是今后研究的重点. [1] SUZUKI Y. Reconfigurable modular robot adaptively transforming a mechanical structure [J]. J Robot So, 2008, 26(1): 74-81. [2] ØSTERGAARD E H, KASSOW K, BECK R, et al. Design of the ATRON lattice-based self-reconfigurable robot [J]. Autonomous Robots, 2006, 21(2): 165-183. [3] MOECKEL R, JAQUIER C, DRAPEL K, et al. Exploring adaptive locomotion with YaMoR, a novel autonomous modular robot with bluetooth interface [J]. Industrial Robot: An International Journal, 2006, 33(4): 285-290. [4] SPROEWITZ A, LAPRADE P, BONARDI S, et al. Roombots-towards decentralized reconfiguration with self-reconfiguring modular robotic metamodules [C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, Taiwan: IEEE, 2010: 1126-1132. [5] RYLAND G G, CHENG H H. Design of iMobot, an intelligent reconfigurable mobile robot with novel locomotion [C]// IEEE International Conference on Robotics and Automation. Anchorage, USA: IEEE, 2010: 60-65. [6] ZHAO J, CUI X, ZHU Y, et al. UBot: A new reconfigurable modular robotic system with multimode locomotion ability [J]. Industrial Robot: An International Journal, 2012, 39(2): 178-190. [7] CICERONE S, STEFANO G D, FRIGIONI D, et al. A fully dynamic algorithm for distributed shortest paths [J]. Theoretical Computer Science, 2003, 297(1): 83-102. [8] MOURAD E, NAYAK A. Comparison-based system-level fault diagnosis: A neural network approach [J]. IEEE Transactions on Parallel and Distributed Systems, 2012, 23(6): 1047-1059. [9] GARCIA R, SCHULTZ U, STOY K. On the efficiency of local and global communication in modular robots [C] //IEEE/RSJ International Conference on Intelligent Robots and Systems. St Louis, MO: IEEE, 2009: 1502-1508. [10] MARTIN A, EMAMI M. A fault-tolerant approach to robot teams [J]. Robotics and Autonomous Systems, 2013,61(12): 1360-1378. [11] RANASINGHE N, SHEN W M. Autonomous adaptation to simultaneous unexpected changes in modular robots [C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. San Francisco, CA: IEEE, 2011. [12] GUAN E G, YAN W X, JIANG D S, et al. A novel design for the self-reconfigurable robot module and connection mechanism [C] //International Conference on Intelligent Robotics and Applications. Shanghai, China: IEEE, 2010: 400-408. [13] DIJKSTRA E W. A note to two problems in connection with graphs [J]. Numerische Mathematik, 1959, 1(2): 269-271. Fault Self-diagnosis for Modular Robotic System Based on Modified Dijkstra Method GUANEn-guang,FUZhuang,YANWei-xin,ZHAOYan-zheng (Research Institute of Robotics, Shanghai Jiaotong University, Shanghai 200240, China) A novel fault self-diagnosis strategy for modular robotic system is presented. The strategy consists of two parts: fault detection and fault message transmission. A healthy pulse method is used to realize the exogenous detection. And the Dijkstra method is modified to be capable of guiding the passage of fault messages along the optimal path. Computational simulations of one system form, M-Lattice, have demonstrated the validity and reliability of the proposed strategy. And the strategy should be applicable in modular robotic systems in general. modular robotic system; fault self-diagnosis; M-Lattice modular robot 1671-0444(2015)06-0788-07 2014-09-03 国家自然科学基金资助项目(60875058, 61473192) 管恩广(1983—),男,山东胶州人,博士研究生,研究方向为模块机器人控制算法.E-mail: enguangovo@sjtu.edu.cn 赵言正(联系人),男,教授,E-mail: yz-zhao@sjtu.edu.cn TP 206; TP 242 A
3 故障自诊断策略仿真






4 结 语

