基于非对称时间满意度的易逝品供应链鲁棒性模型

陈　炜,石春乐,杨以雄

(东华大学 a.旭日工商管理学院；b.服装与艺术设计学院；c.现代服装设计与技术教育部重点实验室，上海 200051)

基于非对称时间满意度的易逝品供应链鲁棒性模型

陈炜a,石春乐a,杨以雄b,c

(东华大学 a.旭日工商管理学院；b.服装与艺术设计学院；c.现代服装设计与技术教育部重点实验室，上海 200051)

鉴于易逝品产业发展的市场需求和易逝品供应链自身的复杂性，以及其较低的抗风险能力，正确度量易逝品供应链网络的鲁棒性可为决策者提供有效决策依据.在分析易逝品供应链鲁棒性主要影响因素的基础上，构建基于非对称时间满意度函数的易逝品供应链鲁棒性度量模型.通过算例验证模型的有效性，并在供应链各类故障情境下，分析了供应链鲁棒性的敏感度.

易逝品供应链；鲁棒性；非对称时间满意度；风险；敏感性分析

易逝品是指具有生产提前期长、销售期短、期末未售出的商品残值极低甚至还需处理成本，市场需求不确定性大等显著特征的某类产品[1].打造快速反应供应链已成为易逝品企业抢占市场至关重要的手段.缩短从策划、开发设计、原料采购、生产到产品上柜的前置时间成为易逝品供应链绩效评价的核心；供货数量准确性以及供应链自身的抗风险能力和供应链节点位置也是不可忽视的影响因素.供应链故障及延误是指供应链的某个或多个环节出现无法满足预期需求的现象，致使供应链无法正常运行，并对供应链企业的短期和长期效益造成不良影响，增加成本和库存，从而降低供应链竞争力.由于易逝品供应链的复杂性和不确定性，要求供应链提高自身的鲁棒性(稳定性)，即提高维持自身功能的稳定能力[2]，进而要求增强协作及抵御风险的能力.因此，有必要从整体角度度量易逝品供应链的鲁棒性及分析供应链出现故障时易逝品供应链的鲁棒性变化.

供应链鲁棒性及供应链故障研究[3-9]是当前国内外研究的热点.文献[10]系统分析了运营管理和决策支持系统中的鲁棒性.文献[11]通过具有随机离散性的时间控制动力系统，得出供应链网络物流控制的优化模型.文献[12]在不确定性条件下构建具有预测控制的供应链鲁棒性绩效模型.文献[13]提出在不确定性环境下，通过鲁棒性、灵敏度、信息共享、决策和市场力等理论拓展供应链管理理论范畴.但当前研究多侧重鲁棒优化模型的构建，或鲁棒性供应链的设计再造，对于供应链整体鲁棒性度量的研究[14]甚少.为此，本文在前人研究基础上，分析易逝品供应链鲁棒性相关影响因素，构建基于非对称时间满意度的易逝品供应链鲁棒性度量模型，通过鲁棒性度量以及鲁棒性的敏感性分析，提出一种评价易逝品供应链鲁棒性的方法，作为供应链鲁棒性评价和改善的依据.通过敏感性分析，得出影响供应链网络鲁棒性变化的若干结论，为测评和提高易逝品供应链鲁棒性提供有效工具和借鉴.

1　非对称时间满意度函数

时间竞争是易逝品供应链的竞争要点，只有将产品在正确的时间送至店铺(客户)，才能抓住消费时机，避免剩货和机会损失.时间满意度是指客户对产品从下单到送达所用时间的满意程度.时间满意度会随送达时间的不同而变化.时间满意度函数可以定义为：客户时间满意度(因变量)与配送到达时间在规定时间限制内的数学关系(自变量)[15].一般而言，该数学关系式左右对称[16]，但易逝品时效性强，单位时间内延迟到货的损失要大于提前到货的损失，而损失越高则满意度越低，即为非对称的满意度函数.本文借鉴文献[17]基于到达时间的非对称分段价值函数，并将问题简化为线性分段函数，所构建的易逝品客户满意度趋势图如图1所示.由图1可以看出，梯形函数的右腰相对陡峭.

图1中，客户的满意度取值区间为[0,1]，满意度变化呈线性.表示客户k对产品到达的时间完全满意区间；同时客户还有一个能够接受的最大到达时间区间，产品到达时间早于FTk或晚于，都会使客户感到某种程度的不满意；而当产品到达时间早于ZTk或晚于，都会使顾客感到完全不满意.其中，[ZTk,FTk]为满意度递增区间，为满意度递减区间，但后者的变化率(直线斜率绝对值)大于前者的变化率.客户k对产品到达时间Tk的非对称时间满意度函数S(Tk)表示为

(1)

2　鲁棒性模型的建立

2.1问题描述与参数设置

供应链可描述为与时间和数量相关的不确定性系统[18]，而各种不确定性所导致的供应链功能失调乃至故障的可能性及危害即为供应链风险[19].本文以易逝品供应链满足最终用户需求的能力作为供应链鲁棒性的度量依据.以时间、供应能力(数量)以及供应链各节点和边(节点间的连接)自身的抗风险能力作为供应链鲁棒性的3个评价维度.其中，时间以客户时间满意度作为评价维度；产品数量以实际产品供应数量与期望产品供应数量的比率即供应比率作为评价维度；考虑供应链各节点与边自身抗风险能力的交互影响.

在此，考虑一个包含供应商Si(i=1,2,…,s)、制造商Mj(j=1,2,…,m)、分销商Dn(n=1,2,…,d)、终端客户L的4级供应链网络的鲁棒性评价问题.将最终客户看成一个集体，即最终用户设为1.节点Si与Mj之间的连接(边)为WSiMj，同理，节点Mj与Dn之间的边为WMjDn，节点Dn与L之间的边为WDnL.网络中包括的供应路径数目为Cg(g=1,2,…,c).

(1) 时间维度.时间维度即前置时间的鲁棒性，是易逝品供应链鲁棒问题的关键.设置实际前置时间为Tk，而最终客户的时间满意度函数为S(Tk).供应商Si订货到交货的总时间为TSi；制造商Mj的生产时间为TMj；分销商Dn的供货处理时间为TDn.节点Si与Mj之间的运输时间为TSiMj.同理，节点Mj与Dn之间的运输时间为TMjDn；节点Dn与L之间的运输时间为TDnL.

(2) 供应能力维度.供应能力维度以供应比率作为度量依据.设供应链期望的产品供应数量为QE.供应商Si的最大供应能力为PSi，分配的供应能力为QSi；制造商Mj的最大供应能力为PMj，分配的供应能力为QMj；分销商Dn的最大供应能力为PDn，分配的供应能力为QDn.节点Si与节点Mj间的最大供应能力(运输能力)为PSiMj，分配的供应能力为QSiMj.同理，节点Mj与Dn之间的最大供应能力为PMjDn，分配的供应能力为QMjDn；节点Dn与L之间的最大供应能力为PDnL，分配的供应能力为QDnL.

(3) 抗风险能力维度.供应链各节点与边抗风险能力的交互作用是评价供应链鲁棒性的一个维度，与节点的地理位置有关.节点与边的抗风险能力取值在0～1，即R∈[0,1]，数值越大代表抗风险能力越强.设置供应商Si的抗风险能力为RSi；制造商Mj的抗风险能力为RMj；分销商Dn的抗风险能力为RDn.节点Si与Mj之间连接(边)的抗风险能力为RSiMj；节点Mj与Dn之间边的抗风险能力为RMjDn；节点Dn与L之间边的抗风险能力为RDnL.

考虑节点与边的归属.设XSi，XMj，XDn为0～1的变量，分别表示Si，Mj，Dn是否归属于当前的供应链网络；又设XSiMj，XMjDn，XDnL也为0～1变量，表示两节点之间是否有连接，即边是否归属于当前的供应链网络，变量具体定义如下：

2.2易逝品供应链鲁棒性模型设计

(1) 时间满意度鲁棒性α

Tk=max(TSi×XSi+TSiMj×XSiMj+TMj×XMj+

TMjDn×XMjDn+TDn×XDn+TDnL×XDnL)

(2)

α=S(Tk)

(3)

式(2)表示以供应链网络中最晚到货的供应路径总完成时间作为实际供货完成时间Tk，并代入时间满意度函数S(Tk)，求得时间维度的供应链鲁棒性数值α.

(2) 供应能力鲁棒性β

(4)

式(4) 实际上计算的是实际供应能力占期望供应数量QE的比率，大括号内各项参数是构成供应链网络各节点与边的实际供应能力的最小值，表示各阶段约束能力，取大括号中各项的最小值表示供应链的约束瓶颈，即有效产出的关键制约因素[20]，也就是供应链网络的实际供应能力.

(3) 供应链节点与边自身抗风险能力γ

(5)

式中：

(6)

式(5)为供应链网络的抗风险能力.网络中每条供应路径中各节点与边抗风险能力相乘为各条供应路径的抗风险能力，而各条供应路径风险能力之和即为整个供应链网络的抗风险能力，最后除以供应路径数目Cg，使γ的取值在[0,1].

将供应链鲁棒性分解成时间满意度、供应能力、抗风险能力3个因素后，可设整个供应链网络的鲁棒性Z是这3个因素的函数，即

Z=f(α,β,γ)

(7)

因素分解的模型方法有很多，相对而言乘法模型应用较广泛[21]，则Z的最终表达式为

Z=α×β×γZ∈[0,1]

(8)

3　算例及鲁棒性的敏感性分析

3.1基本数据

算例基本数据结构源于E品牌服装公司的快速反应供应链.E品牌服装公司在国内拥有6个子品牌，超过2 500家门店，经营以女装为主的快时装产品.2009年至今，通过与东华大学及麦肯锡咨询团队的合作，对企业供应链业务流程进行了改革和优化，面对快时尚行业的激烈竞争，提出增加快速反应订单、快速追单以及缩短产品开发制造周期的解决方案，以提高企业经营效益.

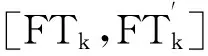
图2　案例供应链网络结构Fig.2　Supply chain network structure of the case

其他初始数值设置如表1和2所示.表1中T*为单位产品的生产时间(即平均节拍，为一件产品的标准总加工时间除以作业人数)，表2中TW为各边的运输时间,P，Q，R分别为节点或边的最大供应能力、分配的供应能力和抗风险能力.本算例数值模拟的是时间满意度落在满意递减区间的情形，该情形在实际问题中较为普遍，模型分析具有代表性.

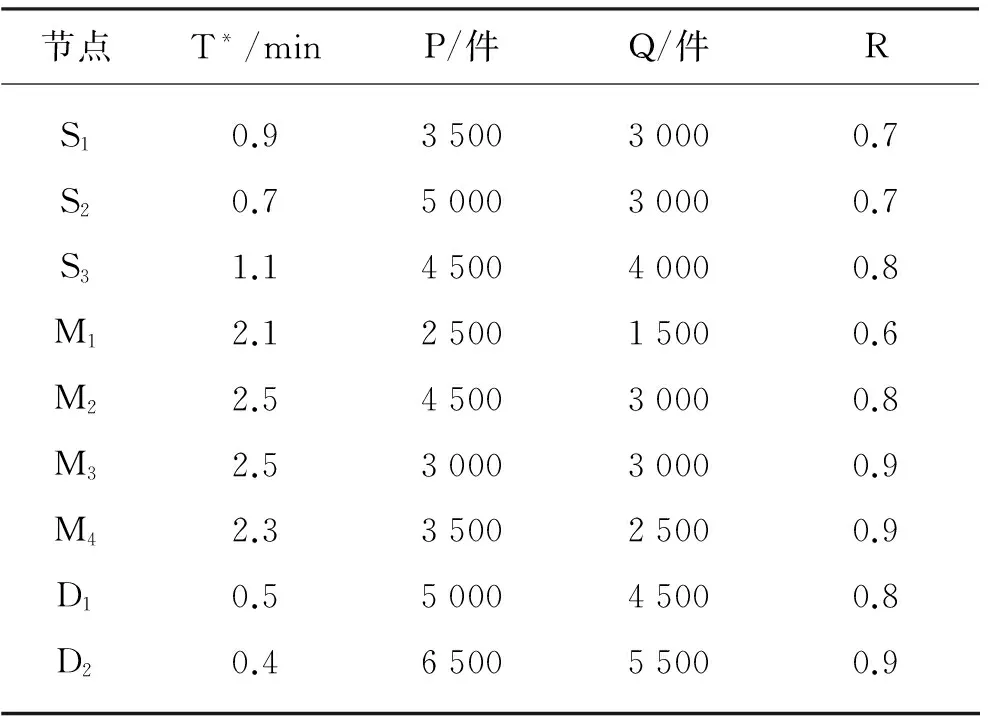
表1 易逝品供应链各节点的初始值Table 1　Initial values of each node in perishables supply chain

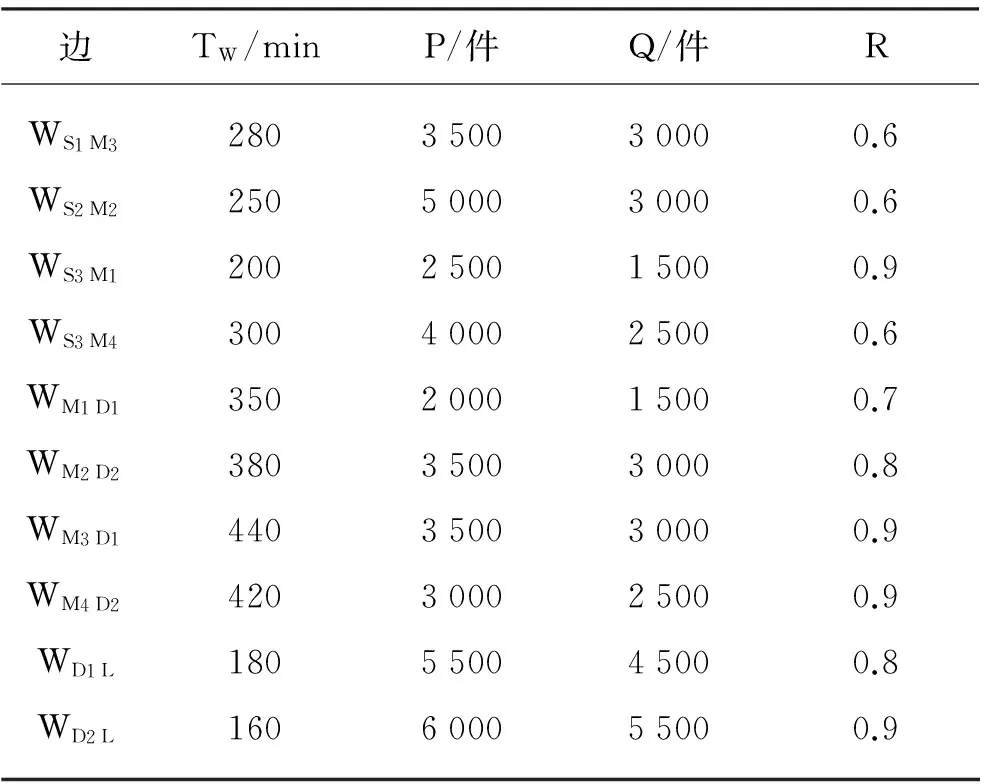
表2　易逝品供应链各边的初始值Table 2　Initial values of each edge in perishables supply chain

首先，将表1和2中的相关数据代入式(2)，可得到产品到达时间Tk=12600 min.将上式计算结果依次代入式(1)和(3)，可求得时间满意度鲁棒性α=0.96.再将表1和2中的相关数据分别代入式(4)和(5)，求得β=1，γ=0.23598.最后，根据式(8)求得供应链网络的鲁棒性Z=α×β×γ=0.96×1×0.23598=0.2265.

由此求得案例企业易逝品供应链网络的鲁棒性为0.2265，该数值可作为决策者评判易逝品供应链可靠性及稳定性的参考依据.

3.2鲁棒性的去节点敏感度

假设节点M1发生故障，即不能完成原先分配的供应能力，且由于供应链反应时间的限制，无法安排其他制造商顶替未完成的生产任务.设该节点故障后实际完成的供应能力占原先分配供应能力的比例为θa，且M1分配的供应能力为QM1，则M1当前实际能完成的供应能力为QM1·θa.

由图2可知，供应链网络中共有4条供应路径，各条供应路径的抗风险能力设为RCn(n=1,2,3,4)，其中M1所在供应路径的抗风险能力设为RC3.在故障发生后，故障节点的抗风险能力评估值下降，本文设M1抗风险能力降低为RM1·θa，显然可得M1所在供应路径的抗风险能力为RC3·θa，根据式(8)，简化可得到

(9)

由于除变量θa外，其他均为已知量，故一阶求导可得

(10)

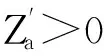
(11)

通过敏感性分析可以从定量的角度研究供应能力变化对供应链网络鲁棒性的影响程度.供应链网络鲁棒性对于节点供应比率的敏感度计算式如式(10)所示.

(12)

式中：Za为θa取值所对应的供应链鲁棒性.当a=0时，θ0=1，代入式(9)可求得Z0；当a=1时，θ1=0.9，代入式(9)可求得Z1；当a=2时，θ2=0.8，代入式(9)可求得Z2；其他依次类推.

以θa的均匀变化(Δθa=10%)分析去节点供应链鲁棒性的敏感度，结果如图3所示.由图3可以看出，敏感度Ea随着θa的均匀递减而递减，图中起点(E1=0.352 0)为Z1相较Z0的变化率与θ1相较θ0变化率之间的比值.

由此可知，供应链鲁棒性随节点完成原定供应能力的比例θa的增大而变大，且增大的速度越来越快.即供应链鲁棒性随着θa的减小而减小，但减小的速度越来越慢.并且供应链鲁棒性的敏感度随着节点供应能力的减弱而减小.

3.3鲁棒性的去边敏感度

假设边WM4D2发生故障，即不能完成原先安排的运输能力，且同样因供应链反应时间的限制，无法安排其他线路替代未完成的运输任务.设该边故障后实际完成的运输能力占原先安排运输能力的比例为μb，并已知WM4D2原先分配的运输能力为QM4D2，则WM4D2当前能完成的运输能力降为QM4D2·μb，并可得其他路径完成的运输能力为QE-QM4D2.边WM4D2所在供应路径的抗风险能力为RC4，故障发生后，该边的抗风险能力降低为RM4D2·μb，并可得该边所在供应路径的抗风险能力为RC4·μb.根据式(8)转化得

(13)

由于除变量μb外，其他均为已知量，故一阶求导得

(14)

又因θb∈(0,1]，所以，可得鲁棒性Zb随μb单调递增.又因二阶求导

(15)

以μb的均匀递减(Δμb=10%)分析去边供应链鲁棒性的敏感度.参照式(12)，可求得供应链的去边敏感度如图4所示.由图4可以看出，去边敏感度(Eb)随着μb的均匀递减而递减.

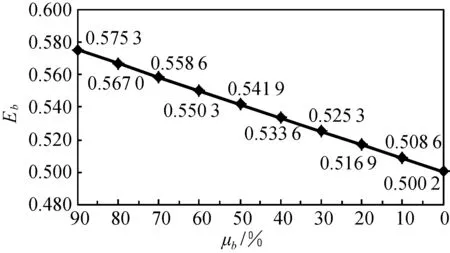
图4　μb递减(Δμb=10%)时鲁棒性的敏感度变化Fig.4　Sensitivity change of robustness when μb is decreasing uniformity (Δμb=10%)

由式(14)和(15)推论可知：供应链鲁棒性随着边完成运输能力μb的增大而增大，且增大的速度越来越快，即供应链鲁棒性随着μb的减小而减小，但减小的速度越来越慢.而图4说明供应链鲁棒性的敏感度随着μb的递减而减小.

3.4鲁棒性的时间敏感性分析

假设节点S2连接路径因故障而延时供应，即不能按原定时间TS2将产品运输到完成生产.设实际完成时间与原定时间的比例为ωc，即实际完成时间为TS2·ωc，再根据时间满意度函数可求得时间鲁棒性α.该节点的抗风险能力降低为RS2/ωc.各条供应路径的前置时间设为TCn(n=1,2,3,4).以ωc的均匀变化分析鲁棒性的时间敏感性.供应链鲁棒性对于时间敏感度系数计算式如式(16)所示.

(16)

式中：Zc为ωc取值所对应的供应链鲁棒性.当c=0时，ω0=1，代入式(9)可求得Z0；当c=1时，ω1=1.1，代入式(9)可求得Z1；当c=2时，ω2=1.2，代入式(9)可求得Z2；其他依次类推.而当c=h时，Zh=0.

以ωc的均匀增大(Δωc=10%)分析供应链鲁棒性及鲁棒性的时间敏感度，结果如表3和图5所示，其中ΔZc为该行的鲁棒性Zc与上一行鲁棒性的差值.

表3　易逝品供应链鲁棒性及时间敏感性分析Table 3　Robustness and time sensitivity analysis of perishables supply chain

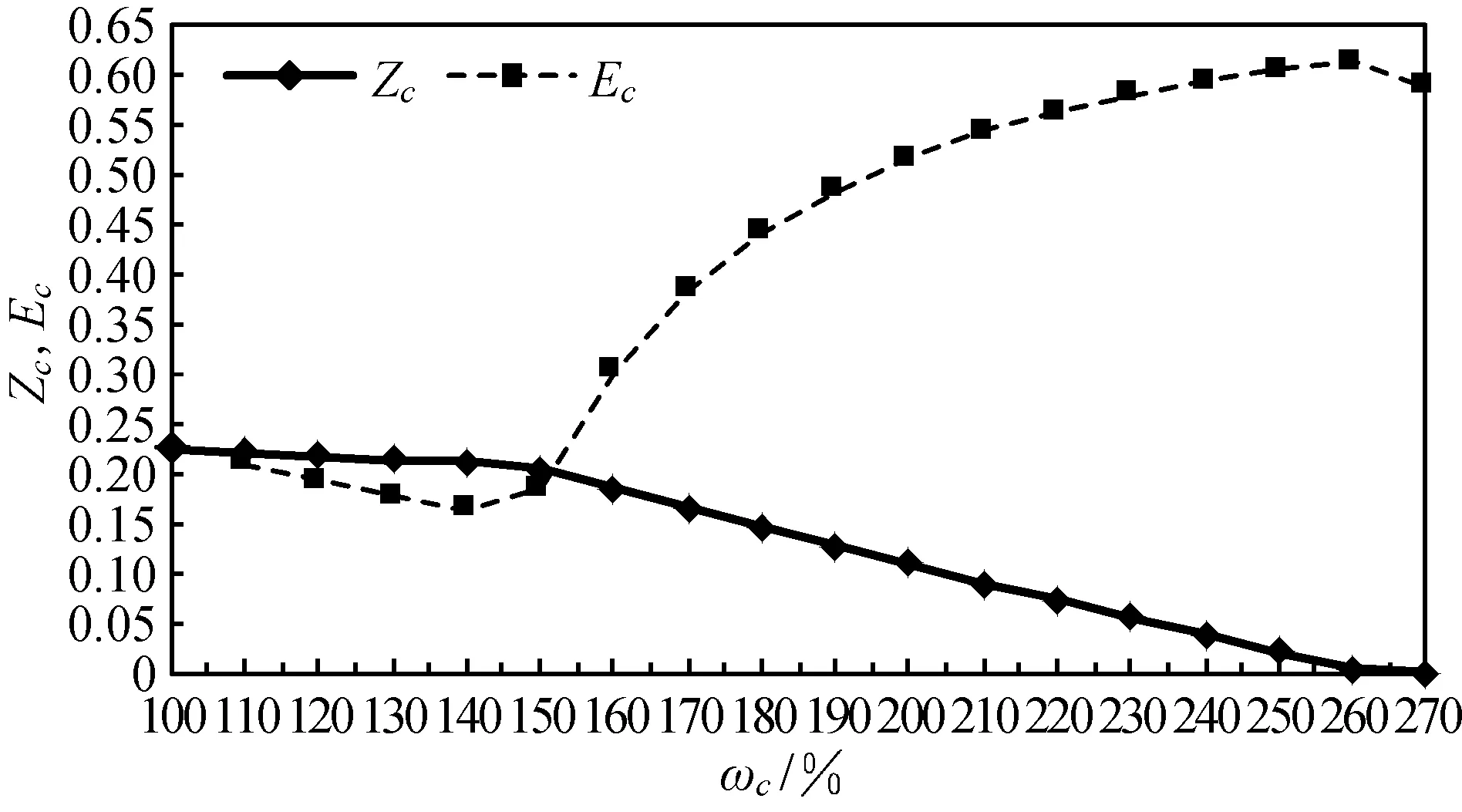
图5　ωc递增(Δωc=10%)时鲁棒性及鲁棒性敏感度变化Fig.5　Robustness and its sensitivity change when ωcis decreasing uniformity (Δωc=10%)

由表3可知，ΔZc为负值，即供应链鲁棒性与ωc负向相关.由图5可见，在故障节点所在供应路径非最晚到货的供应路径前提下，即延时后S2所在供应路径的实际前置时间TC2Tk，即TC2为最晚到货供应路径且满意度递减时，供应链鲁棒性也随着ωc的增大而减小.但TC2>Tk时,鲁棒性降低速度要显著大于TC2

若故障节点所在供应链为最晚到货供应链，则供应链鲁棒性及鲁棒性的敏感度变化与上述例子TC2>Tk时的变化趋势相同.同样，对边的时间敏感性分析也可得到以上相似结果，本文不再赘述.

4　结　语

本文针对易逝品供应链快速响应的特点，提出易逝品供应链鲁棒性影响因素有：前置时间满意度(T)；供应链产品供应能力完成情况(P,Q)；与节点地理位置相关的各节点与边的抗风险能力(R).综合以上3个影响方面得出易逝品供应链鲁棒性度量模型，为易逝品供应链管理问题提供一种新的研究思路.

通过供应链鲁棒性的敏感性分析，得到节点和边发生故障及时间延误时，节点或边的抗风险能力对易逝品供应链鲁棒性(Z)有显著的正向影响.易逝品供应链鲁棒性和鲁棒性敏感度(E)随着节点或边供应能力的递减而递减，但鲁棒性递减的速度越来越慢，而敏感度的递减则基本呈线性.在故障节点或边所在供应路径非最晚到货供应路径的前提下，易逝品供应链鲁棒性随着节点或边延误时间比(实际供应时间与原定时间之比ωc)的递增而递减，而鲁棒性敏感度则基本呈先微弱递减后显著递增的趋势.

本文研究的易逝品供应链鲁棒影响因素仍有局限性，如鲁棒性影响因素可设置权重差别，另外，供应链仅涵盖到易逝品上柜时段，考虑消费者需求变化及不确定性对供应链鲁棒性的影响也值得进一步探讨.

[1] 曹细玉,宁宣熙.考虑退货价格的易逝品供应链协调性研究[J].管理科学，2007,20(2):31-35.

[2] 接婧.国际学术界对鲁棒性的研究[J].系统工程学报，2005,20(2):153-159.

[3] PISHVAEE M S,RAZMI J,TORABI S A.Robust possibilistic programming for socially responsible supply chain network design: A new approach[J].Fuzzy Sets and Systems，2012,206:1-20.

[4] YANG Z B,AYDIN G,BABICH V,et al.Supply disruptions,asymmetric information,and a backup production option[J].Management Science,2009,55(2):192-209.

[5] HASANI A,ZEGORDI S H,NIKBAKHSH E.Robust closed-loop supply chain network design for perishable goods in agile manufacturing under uncertainty[J].Source: International Journal of Production Research,2012,50(16):4649-4669.[6] SARKAR A,MOHAPATRA P K J.Determining the optimal size of supply base with the consideration of risks of supply disruptions[J].International Journal of Production Economics,2009,119(1):122-135.

[7] XU X,ZHAO Y.Price-only contracts with backup supply[J].Operations Research Letters,2010,38(3):201-206.

[8] KOMOTO H,MISHIMA N.A simulation system to analyze effects of relocation of machine tools on supply chain robustness[J].International Journal of Automation Technology,2012,6(3):304-311.

[9] LI J,WANG S,CHENG T C.Competition and cooperation in a single-retailer two-supplier supply chain with supply disruption[J] .International Journal of Production Economics,2010,124(1):137-150.

[10] ROY B.Robustness in operational research and decision aiding: Amulti-faceted issue[J].European Journal of Operational Research,2010,200(7):629-638.

[11] LAUMANNS M,LEFEBER E.Robust optimal control of material flows in demand-driven supply networks[J].Physica A: Statistical Mechanics and Its Applications,2006,363(1):24-31.

[12] LI X,MARLIN T E.Robust supply chain performance via model predictive control[J].Computers and Chemical Engineering,2009,33(12):2134-2143.

[13] WALLACE S W,CHOI T M.Flexibility,information structure,options,and market power in robust supply chains[J].International Journal of Production Economics,2011,134(2):284-288.

[14] 唐莉莉.供应链的鲁棒性度量及敏感性分析[D].天津:天津大学管理与经济学部,2011:16-29.

[15] 胡觉亮,吴丽华,韩曙光,等.基于时间满意度的服装配送模型与算法研究[J].纺织学报,2010,31(2):138-142.

[16] 马云峰.网络选址中基于时间满意的覆盖问题研究[D].武汉:华中科技大学管理学院,2005:46-48.

[17] JOU R C,KITAMURA R,WENG M C,et al.Dynamic commuter departure time choice under uncertainty[J].Transportation Research Part A: Policy and Practice,2008,42(5):774-783.[18] ARNS M,FISCHER M,KEMPER P,et al.Supply chain modeling and its analytical evaluation[J].Journal of the Operation Research Society,2002,53(8):885-894.

[19] 朱怀意,朱道立,胡峰.基于不确定性的供应链风险因素分析[J].软科学,2006,20(3):37-41.

[20] 杨以雄,杞文楠,郜雅,等.服装供应商制造周期效能的提高及案例分析:订单排程与投料管控[J].东华大学学报：自然科学版，2012,38(2):229-233.

[21] 徐国祥.统计学[M].上海:上海人民出版社,2007:294-295.

Robust Model of Perishables Supply Chain Based on Asymmetric Time Satisfaction

CHENWeia,SHIChun-lea,YANGYi-xiongb,c

(a.Glorious Sun School of Business and Management；b.Fashion and Art Design Institute; c.Key Laboratory of Clothing Design and Technology,Ministry of Education,Donghua University,Shanghai 200051,China)

Due to the demand for the development of perishable products industry,perishables supply chain’s complexity and its weaker anti-risk ability,the accurately measurement of the perishables supply chain’s robustness can provide the decision-maker with an effective basis for decision-making.Upon analyzing the main factors of perishables supply chain network robustness,an perishables supply chain robust model based on asymmetric time satisfaction function has been put forward.Numerical examples demonstrating the effectiveness of the model are given,and the sensitivity of supply chain robustness is analyzed under the situations of different supply chain faults.

perishables supply chain; robustness; asymmetric time satisfaction; risk; sensitivity analysis

1671-0444(2015)02-0253-07

2013-11-07

中央高校基本科研业务费专项资金资助项目(12D21501，13D121504，CUSF-DH-D-2014068)；上海高校知识服务平台(海派时尚设计及价值创造知识服务中心)资助项目(13S1070241)；上海市科技发展基金软科学研究博士生学位论文资助项目(12692190500)；东华大学非线性科学研究所专项资金资助项目(INS-1401)

陈炜(1985—)，男，浙江台州人，博士研究生，研究方向为服装产业经济与供应链管理.E-mail: 9006623@163.com

杨以雄(联系人)，男，教授，E-mail: yyx@dhu.edu.cn

F 224

A