弓网振动试验系统的改进幅相自适应控制设计

魏巍，杨志东，韩俊伟

(哈尔滨工业大学机电学院，黑龙江哈尔滨150000)

弓网关系是高速列车能否安全有效运行的关键环节［1-4］。弓网振动试验台在弓网动态关系的模拟试验中发挥着重大作用，为了模拟高速列车运行时的状态，弓网试验台的振动频率需要达到100 Hz［5］。在高频振动试验中，正弦运动信号是很常见的一种信号。为了精确重现某一复合运动，需要不同自由度之间的正弦运动能精确跟踪各自的给定信号［6］。由于电液伺服系统自身固有频率的限制，以及各种非线性因素的影响，采用传统PID的位移闭环控制策略，很难实现高频下正弦信号的精确跟踪［7-8］。目前对正弦运动精确控制的方法主要有变结构控制和自学习等［9-10］。张元生等提出的基于频域的谐波幅相自适应控制(HAPAC)方法［6］，通过对输入输出信号在频域的谐波辨识补偿，提高了正弦运动的动态跟踪性能，不过该方法需要提前确定系统的初始模型，辨识速度取决于初始模型的精确程度。Yao和马建明等提出了基于Widrow-Hoff神经网络学习算法的幅相控制策略［11-12］，该控制策略将给定信号和跟其相位相差90°的信号以一定的加权系数叠加，通过LMS算法调整权值向量，实现正弦信号的跟踪。不过该算法中初始加权值和学习系数的选择容易影响系统的稳定性。另外，上述两种控制策略无法对正弦信号的中心位置偏差进行修正。为此，本文基于时域给出幅相自适应控制的改进算法、计算机实现方法以及弓网试验系统对该算法的实验验证。实验结果表明，改进幅相控制算法可以有效克服上述传统控制策略的缺点，实现正弦运动信号的精确跟踪。

1 弓网振动试验系统描述

弓网振动试验系统主要由3部分组成:外框、中框和内框。如图1所示，外框由两组伺服电机和竖直方向的丝杆导轨结构组成，模拟受电弓垂直方向的大幅值低频运动;中框由两组伺服电机和水平方向的丝杆导轨结构组成，模拟受电弓水平方向的运动;内框由伺服阀控制的激振缸驱动，模拟垂向小幅值高频振动。

图1 弓网试验系统Fig.1 Pantograph-catenary test system

外框和中框的工作频率较低，与内框的电液伺服系统相比，伺服电机没有太多的非线性因素影响，因此，外框和中框对给定信号的跟随性较好，采用传统的控制策略就能满足精度要求。内框采用的是液压驱动，需要对100 Hz的高频正弦信号进行精确复现。由于液压系统频宽的限制，以及摩擦、死区、间隙和流量方程等非线性因素的影响，内框在运行过程中表现为较强的时变非线性［13-15］。此外，该试验系统的控制周期为1 ms，而内框要求25 Hz正弦运动时相位滞后需在5°以内，即滞后时间为0.56 ms，小于试验系统的控制周期，传统的PID前馈控制以及幅相控制策略无法满足该精度要求。

2 改进幅相自适应控制策略

改进幅相自适应控制模块主要分为两个部分:辨识和迭代，如图2所示。理想正弦信号和反馈正弦信号通过辨识模块进行比较，辨识出幅值误差ΔA，相位误差ΔPhase和中心位置误差ΔBias，并将结果输入迭代模块。迭代模块根据当前偏差值对正弦给定信号的3个参数进行迭代修正，使得反馈信号可以精确跟踪正弦信号。

图2 改进幅相自适应控制模块的组成Fig.2 Composition of the MAPAC module

弓网振动试验系统下位机的实时运行代码通过快速原型的方式开发。幅相自适应模块基于Stataflow图形工具进行开发。有限状态机Stataflow在解决复杂的逻辑问题方面很占优势，图形化的编程方式也更为直观和简洁，且其本身与Simulink之间能实现无缝连接。

2.1 辨识模块

辨识模块的主要作用是找出反馈信号与理想信号间的幅值差，相位差和中心位置偏差。显然，辨识出这些误差值，至少需要一个周期的数据，因此辨识模块的辨识周期为一个理想正弦信号的周期。定义单个辨识周期的起始点为理想信号由下而上穿越中位线时刻，结束点为下一次的正向穿越，同时该结束点也是下一个辨识周期的开始点，辨识周期与正弦信号的周期相同，如图3所示。

图3 单个辨识周期Fig.3 Single identification period

幅值误差和中位位置偏差比较容易辨识，幅值误差和中心位置误差分别为

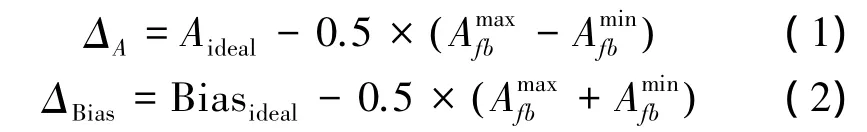
式中:Aideal、Biasideal分别为理想正弦信号幅值和理想中位值，、分别为单个辨识周期内正弦反馈信号的最大值和最小值。通过找到一个周期内正弦反馈信号的最大值与最小值即可辨识出幅值误差和中位误差。

相位误差通过理想正弦信号正向穿越中位线时间和反馈信号的正向穿越中位线时间之间的差值来确定。由于系统的采样及控制周期为1 ms，为了突破控制周期对相位精度的限制，在穿越前的时间点与穿越后的时间点之间进行线性插值，来精确确定穿越时刻。

理想信号的穿越时刻为

式中:tideal为理想信号的穿越时刻;为理想信号穿越后一点的时刻;分别为理想信号穿越前后两点的幅值。反馈信号穿越时刻tfb的计算方法与此类似。

由此可以得到相位滞后为

将相位误差在π处进行如下分段处理:

该处理方式将相位误差范围由 [0，2π]调整至[－π，π]，降低了误差大于π时所需的相位调整量。

通过上面的公式，就可以对一个辨识周期内的ΔA、ΔPhase和ΔBias进行辨识，实现该辨识方法的有限状态机程序如图4所示。程序中的Loop1部分用来确定辨识周期内反馈信号的最大最小值，Loop2部分用来寻找反馈信号穿越中心位置的时间，Loop3部分用来计算ΔA、ΔPhase和ΔBias。

图4 辨识模块的有限状态机程序Fig.4 StataFlow program of identification module

2.2 迭代模块

迭代模块主要是根据辨识模块辨识出的ΔA、ΔPhase和ΔBias，实时修正给定信号的幅值、相位和中心位置。迭代模块的运行周期为系统的控制周期，也就是1 ms。

给定正弦信号的幅值、相位及中位值的迭代序列分别如下:

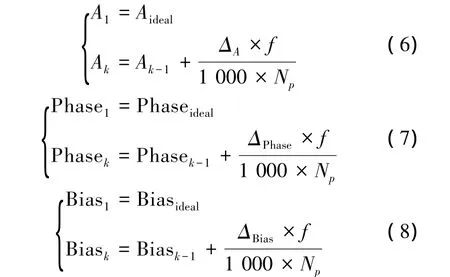
式中:Ak、Phasek和Biask分别为当前控制周期内正弦给定信号的幅值、相位和中位值;Ak－1、Phasek－1和Biask－1分别为上一控制周期的幅值、相位和中位值;f为正弦信号的频率;Np为迭代调整周期，即消除当前偏差所需要经过的正弦周期数。

Np的值越大，则收敛速度越慢，需要经过的迭代周期数越多，时间越长。由于MAPAC模块的辨识周期为一个正弦周期，因此迭代调整周期至少要超过一个正弦周期，才能保证系统的收敛性，所以Np的值要大于1。另外考虑到正弦信号高频时的周期很短，如果Np为某一固定值，频率越大，则迭代时间会越短，而此时幅值衰减和相位滞后也相对较大，过短的迭代调整时间容易造成系统不稳定。因此本文的Np值按如下方式分段选择:

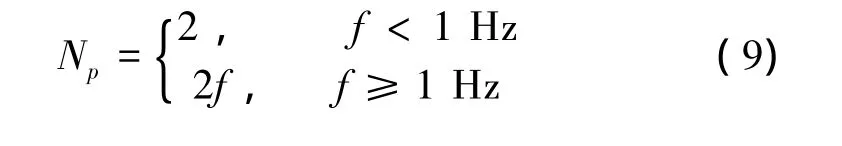
图5 迭代模块的有限状态机程序Fig.5 Stateflow program of iteration module

当正弦信号的频率f在1 Hz以下时，按照两次正弦周期的迭代时间进行迭代运算，当频率f在1 Hz以上时，则变为固定的2 s迭代时间进行迭代运算。Np的分段选取方式兼顾了控制算法在低频时收敛的快速性与高频时的稳定性。迭代部分的有限状态机程序如图5所示。

2.3 改进幅相自适应控制模块

将辨识模块与迭代模块的程序相结合，并将有限状态机StataFlow程序嵌入至Simulink中，得到如图6所示的改进幅相自适应控制模块。图中的iSinStart端口用来指定系统是否启用幅相自适应控制策略。该幅相控制模块中仅需要输入理想正弦信号的相关参数以及正弦反馈信号即可，无需额外设定其他参数，也不需要提前确定系统的初始模型，使用十分便捷。输出端口为实际的给定正弦信号，用该信号作为传统PID控制策略的输入值即可实现幅相控制。

图6 改进幅相自适应控制的Simulink模块Fig.6 Simulik module for MAPAC

3 改进幅相自适应控制的实验结果

为验证本算法在弓网振动试验台上的实际控制效果，用NI的PXI8110工控机对内框的正弦运动信号进行采样及实时控制，其采样及控制周期为1 ms。以带宽为0～150 Hz的随机信号对系统进行激励，经过频谱分析，得到采用经典PID算法时，内框的幅频特性曲线如图7所示，幅值衰减为－3 dB时对应的频率为 24.9 Hz。

图7 弓网试验系统内框的幅频特性Fig.7 Amplitude-frequency characteristic of inner frame in pantograph-catenary test system

分别用25 Hz和80 Hz的高频正弦信号对系统进行激励。不采用MAPAC时，正弦信号的跟踪曲线如图8所示。频率为25 Hz和80 Hz时，幅值误差分别为 6.36%和22%，相位滞后分别为 97.2°和300°，与系统要求的正弦精度指标相差较大。

图8 采用经典PID控制策略的实验曲线Fig.8 Experimental curves under PID control strategy

将MAPAC应用于弓网振动试验系统，采用同样的正弦进行实验，得到正弦实验跟踪曲线如图9所示。25 Hz正弦对应的相位误差降低为0.36°，中心位置穿越处的相位滞后时间仅为0.04 ms，突破了系统控制周期带来的限制。同时，由于系统采样周期为1 ms，频率为80 Hz时，正弦信号一个周期内仅有不到13个数据点，即使在这种情况下，采用MAPAC方法后，依旧可以使反馈信号以高精度跟踪理想信号。由实验结果可以看出，采用改进的幅相自适应控制策略后，系统的正弦跟踪精度有了很大的提高，远远超出原先的精度要求。

图9 采用改进幅相自适应控制的实验曲线Fig.9 Experimental curves under MAPAC

4 结论

本文研究了基于时域的改进幅相自适应控制策略，并将其应用于弓网振动试验系统中来精确跟踪正弦信号。

1)在时域内分析了正弦信号幅值、相位和中心位置的辨识公式，通过线性插值，实现了相位滞后时间的精确辨识。对辨识误差进行迭代控制，给出了迭代序列，并对迭代调整周期进行分段设置，同时满足了系统的快速性和稳定性的要求。

2)给出了辨识和迭代部分的StataFlow程序并对其进行了实验验证，结果表明，改进幅相自适应控制策略能有效提高弓网振动试验系统的正弦跟踪精度，同时还克服了传统幅相控制设定参数繁多、容易发散以及需要提前确定系统初始模型等缺点。

［1］TELLINI B，MACUCCI M，GIANNETTI R，et al.Linepantograph EMI in railway systems［J］.IEEE Instrumentation ＆ Measurement Magazine，2001，4(4):10-13.

［2］WALTERS S，RACHID A，MPANDA A.On modeling and control of pantograph catenary systems［C］//International Conference on Pantograph-catenary Interaction Framework for Intelligent Control.Amiens:Universite de Picardie Jules Verne，2011:54-63.

［3］时菁，杨志鹏，张文轩，等.关节式电分相处的弓网动态特性［J］.中国铁道科学，2014，35(2):46-51.SHI Jing，YANG Zhipeng，ZHANG Wenxuan，et al.Pantograph-catenary dynamic characteristics of articulated phase insulator［J］.China Railway Science，2014，35(2):46-51.

［4］王万岗，吴广宁，高国强.高速铁路弓网电弧试验系统［J］.铁道学报，2012，34(4):22-27.WANG Wangang，WU Guangning，GAO Guoqiang.The pantograph-catenary arc test system for high-speed railways［J］.Journal of The China Railway Society，2012，34(4):22-27.

［5］吴学杰，张卫华，扬世杰.应用于接触网/受电弓混合模拟试验台的计算机测控系统［J］.计算机工程与应用，2002，12:213-216.WU Xuejie，ZHANG Weihua，YANG Shijie.The computer control and measure system applied to the pantograph/catenary mixed dynamic simulation system［J］.Computer Engineering and Applications，2002，12:213-216.

［6］张元生，杨一栋，马智周.三轴转台谐波幅相自适应控制系统的设计［J］.南京航空航天大学学报，2004，36(5):619-622.ZHANG Yuansheng，YANG Yidong，MA Zhizhou.Design of harmonic amplitude-phase adaptive control system in three-axis turntables［J］.Journal of Nanjing University of Aeronautics＆ Astronautics，2004，36(5):619-622.

［7］MERRITT H E.Hydraulic control systems［M］.New York:John Wiley＆ Sons，1967:68-70.

［8］STOTEN D P，SHIMIZU N.The feedforward minimal control synthesis algorithm and its application to the control of shaking-tables［J］.Proceedings of the Institution of Mechanical Engineers.Part I:Journal of Systems and Control Engineering，2007，221(3):423-444.

［9］SHIN K.Adaptive control of active balancing systems for speed-varying rotating machinery［D］.(s.l.):Library of U-niversity of Michigan，2001:113-120.

［10］WEN Haoping.Design of adaptive and basis function based learning and repetitive control［D］.New York City:Library of Columbia University，2001:87-92.

［11］马建明，黄其涛，丛大成.幅相控制策略在六自由度运动模拟器中的应用［J］.哈尔滨工程大学学报，2008，29(11):1217-1221.MA Jianming，HUANG Qitao，CONG Dacheng.Application of the amplitude-phase control strategy in a 6-DOF motion simulator［J］.Journal of Harbin Engineering University，2008，29(11):1217-1221.

［12］YAO Jianjun，DI Duotao，JIANG Guilin，et al.Acceleration amplitude-phase regulation for electro-hydraulic servo shaking table based on LMS adaptive filtering algorithm［J］.International Journal of Control，2012，85(10):1581-1592.

［13］PLUMMER A R.A detailed dynamic model of a six-axis shaking table［J］.Journal of Earthquake Engineering，2008，12(4):631-662.

［14］STEFANO P，RICCARDO R，SALVATORE S，et al.Non-linear modelling and optimal control of a hydraulically actuated seismic isolator test rig［J］.Mechanical Systems and Signal Processing，2013，35(2):255-278.

［15］李洪人.液压控制系统［M］.北京:国防工业出版社，1990:55-58.