基于小波分析的拉萨市近12年污染指数的变化

王　磊, 邓青春, 刘　辉, 张政玲, 李　响

(西华师范大学国土资源学院，四川 南充　637000)

· 大气环境 ·

基于小波分析的拉萨市近12年污染指数的变化

王磊, 邓青春, 刘辉, 张政玲, 李响

(西华师范大学国土资源学院，四川 南充637000)

拉萨作为一个典型的高原城市，研究其空气污染的变化对其他高原型城市具有一定借鉴意义。对拉萨市2001年～2012年的逐日污染指数时间序列进行一维连续Morlet小波变换分析,结果表明:拉萨市的PM10污染指数在不同的时间尺度上有“冬高夏低”变化规律，每年的12月～次年3月是污染的高峰期，夏季集中的降水对空气中PM10污染物有很好的净化作用。分析了不同时间尺度下污染指数的变化规律，得出波动变化的主周期为290d左右，近几年波动幅度有逐渐减弱的趋势。

空气污染指数；PM10；小波分析；拉萨市

1　引　言

近年来，西藏社会经济不断发展，城市化速度不断加快,而拉萨作为其省会城市,在经济持续发展、人口快速增长的背景下，城市的环境问题，尤其是大气污染问题已备受人们关注[1, 2]。通常把空气动力学当量直径在10μm以下的颗粒物称为PM10，又称为可吸入颗粒物,由于粒径小，能被人直接吸入呼吸道造成危害[3]；又由于它能在大气中长期漂浮，易将污染物带到很远的地方，导致污染范围扩大，空气中PM10的含量可以作为评价大气环境质量的标准[4]。据2012年西藏自治区环境状况公报，2012年西藏主要市镇大气环境质量整体优良，拉萨市环境空气质量总体达到了《环境空气质量标准》二级标准,但在拉萨这样一个工业相对落后且为我国大气环境污染防治重点的城市,应该引起人们的警惕[5]。

对城市空气污染一直是学者们比较重视的问题，目前已经有很多对城市空气污染时间序列的研究，例如北京[6]、兰州[7]、重庆[8]、成都[9]、上海[10]等。空气污染时间序列的研究方法多种多样，例如极值统计模型[11]、神经网络方法[12]、重标极差分析以及消除趋势波动分析法[13]等，不同的研究方法都有各自的优势和不足，本文选用小波变换方法来分析拉萨市空气污染指数时间序列，这种方法对处理波动较大的数据具有很好的效果。拉萨作为一个高原城市，其空气污染情况与其他城市有一定差异，鉴于其独特的地理位置和特殊的气候环境，对拉萨的城市空气污染变化情况进行研究是很有必要的。目前对拉萨污染的研究多表现在污染的成因和对策、污染物成因、分布特征以及来源分析，而对空气污染的指数变化研究相对较少[14～17]。本文采用Morlet小波分析了拉萨市近12年来以PM10为主要污染物的逐日空气污染指数变化，分析其在不同时间尺度下的变化规律，对拉萨市的环境监测和防治具有一定的借鉴意义。

2　数据与方法

2.1数据来源

以中华人民共和国环境保护部网站(http://wfs.mep.gov.cn/)数据中心的拉萨市空气质量日报为数据源，衡量空气污染指数的主要污染物为可吸入颗粒物。数据的起止时间为2001年1月1日～2012年12月31日，12年的逐日空气污染指数数据共计4383条，2001年1月1日序号为1，2001年1月2日序号为2，依次类推，2012年12月31日序号为4383，其中2008年6月4日、2010年3月15日和5月21日、2011年10月28日以及2012年11月30日和12月27日的数据缺失，均用前后2天的算术平均值补上。

2.2小波分析方法[18～20]

小波分析是建立在调和分析、泛函分析、样条分析及傅里叶分析基础上的分析处理工具，可以从时域和频域上展示分析对象的局部化特征,从而可以聚焦到对象的任意细节，便于观察任意时间尺度上的变化情况。

小波函数是具有振荡性、能够迅速衰减到零的一类函数，即小波函数ψ(t)L2(R)且满足：

(1)

式中，ψ(t)为基小波函数，它可通过尺度的伸缩和时间轴上的平移构成一簇函数系：

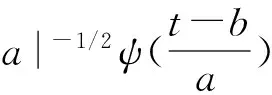
(2)

式中，ψa,b(t)为子小波；a为尺度因子，反映小波的周期长度；b为平移因子，反映时间上的平移。

不同的小波基对相同时间序列的处理结果是不同的，所以选用合适的小波基是小波分析的关键，本文选用的Morlet 小波对分析污染指数时间序列有着良好的效果。

若ψa,b(t)是由(2)式给出的子小波，对于给定的能量有限信号f(t)L2(R)，其连续小波变换(Continue Wavelet Transform，简写为CWT)为：

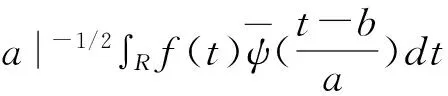
(3)

式中，Wf(a,b)为小波变换系数；f(t)为一个信号或平方可积函数；a为伸缩尺度因子；b为平移参数因子。实际研究中，最主要的就是要由小波变换方程得到小波系数，然后通过这些系数来分析时间序列的时频变化特征。

3　结果与分析

3.1时间序列变化

拉萨市2001年～2012年逐日空气污染指数的逐日变化如图1。可以看出污染指数信号波动强烈并呈现出具有多时间尺度特性，峰值比较明显，在各个阶段出现的位置具有一定的相似性。

图1　拉萨市近12年来的逐日污染指数变化Fig.1　Daily air pollution index change of Lhasa in recent 12 years

如图2所示，将污染指数的分布范围进行归类，可以看出污染指数在100以下的占总数的98.06%，即绝大多数天气拉萨的污染情况都达到了国家二级标准。污染指数在50以下即达到国家一级标准的天数占总数的53.6%。

为便于分析，将每年的3月～5月划分为春季，6月～8月为夏季，9月～11月为秋季，12月～次年2月为冬季，分别对12年中春(图3a)、夏(图3b)、秋(图3c)、冬(图3d)四季的污染指数变化加以分析。数据显示的12年中，污染指数达到国家一级标准(≤50)的日数共有2161d，其中67%集中在夏秋季节(1571d)，33%集中在冬春季节(777d)，污染指数的最低值为9，分别出现在2004年的1月27日、1月28日和7月9日；达到国家二级标准(≤100)的日数共有1947d，其中32%集中在夏秋季节(621d)，68%集中在冬春季节(1326d)；在国家二级标准以上(>100)的日数为85d，其中95%集中在冬春季节(81d)，5%集中在秋季(4d)，夏季空气污染均达到国家二级标准。污染指数的最大值为368,出现在2010年4月26日，属于重污染。对比图3春夏秋冬四季的污染指数可以明显看出，拉萨市冬春季节的污染情况相对严重，而夏秋季节较轻。

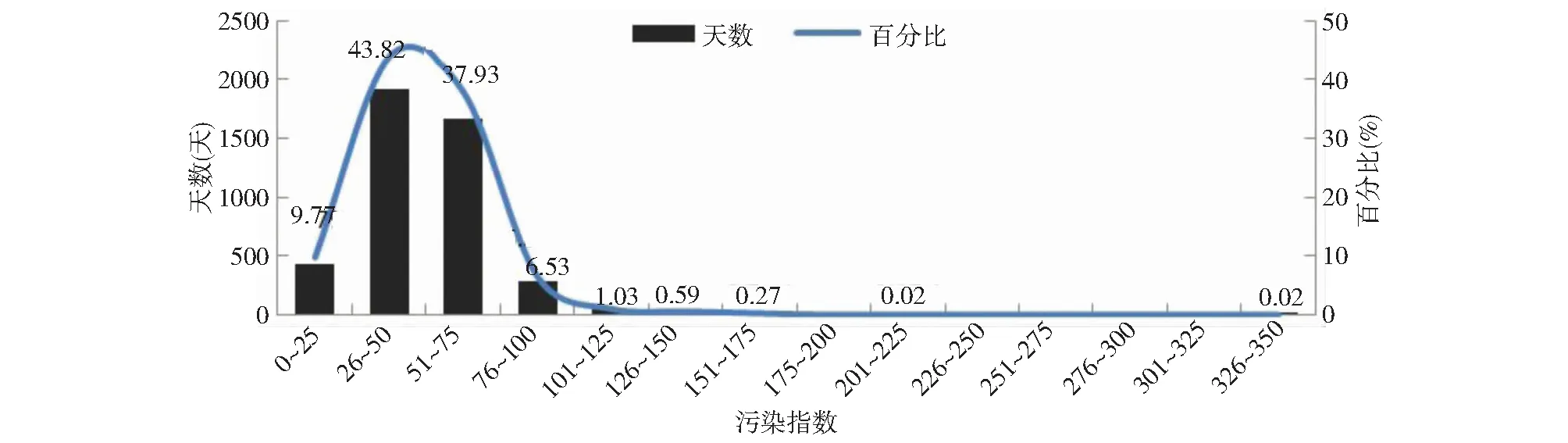
图2　各等级污染天数所占比例Fig.2　The proportion of each grade pollution days

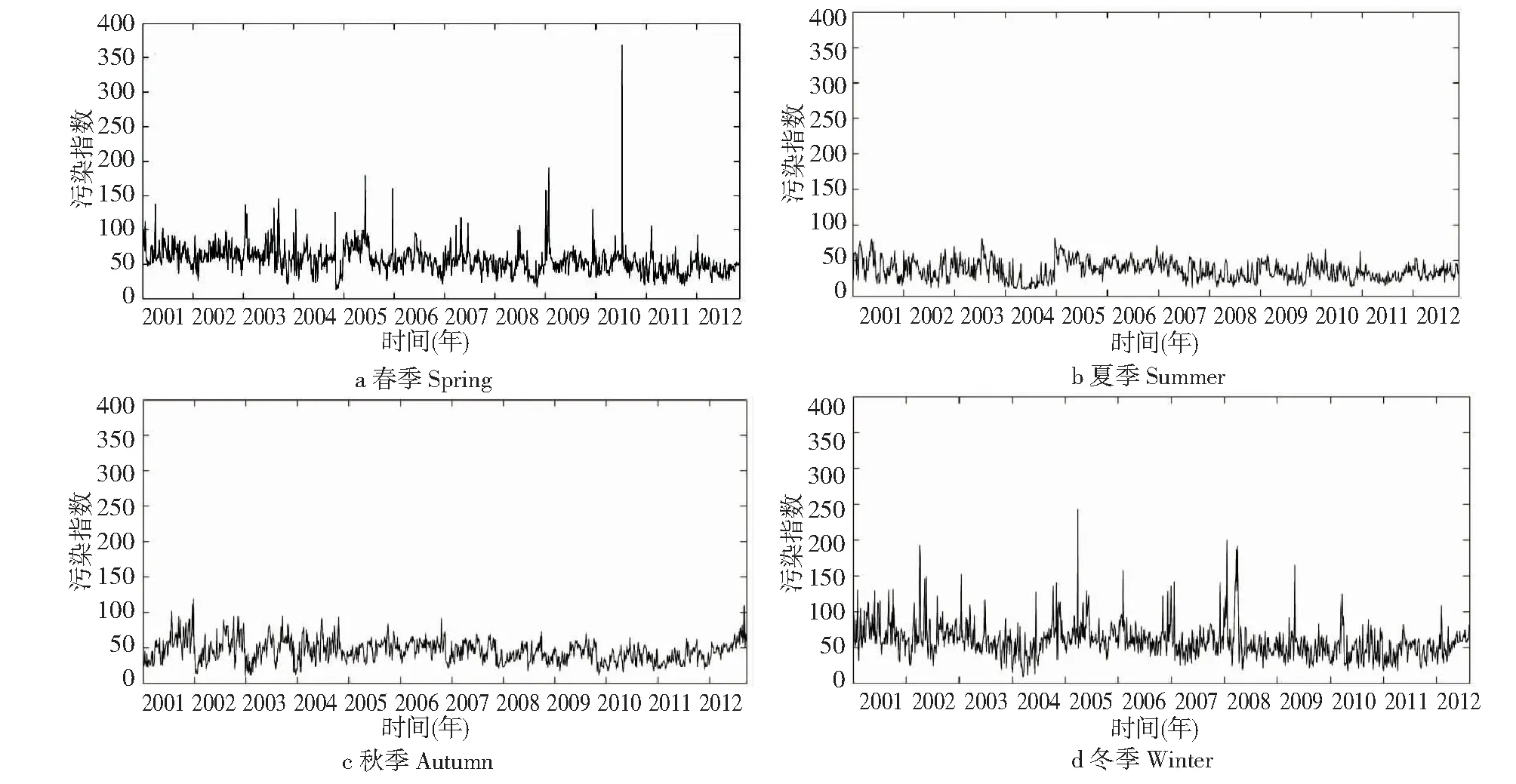
图3　不同季节的空气污染指数Fig.3　Air pollution index in different seasons

3.2污染指数的多尺度变化特征

图4显示了拉萨市近12年来污染指数在不同时间尺度上的振荡特征，波动信号强弱通过小波系数的大小来表示：图中的灰度值越大表示小波系数越小，污染越轻；反之，灰度值越小表示小波系数越大，污染越严重。

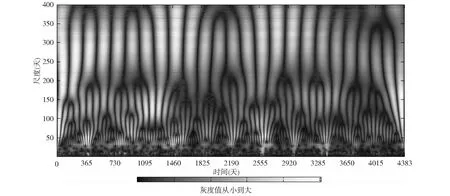
图4　污染指数的时间-尺度分布Fig.4　The time-scale distribution of air pollution index

图4中自上而下分别对应较长时间尺度和较短时间尺度的周期性振荡。图中尺度在200d以上的灰度振荡较明显，灰度值较大的区域主要集中在年中部分，即夏秋季节；灰度值较小的区域主要集中在年初和年末，即冬春季节。不同尺度下的污染指数变化特征表现为小尺度变化包含于大尺度变化之中。

在不同的时间尺度上进行更为详细的波动变化分析，本文分析了365d、180d、90d、60d、30d和7d这6个时间尺度的污染指数变化特征(图5)。

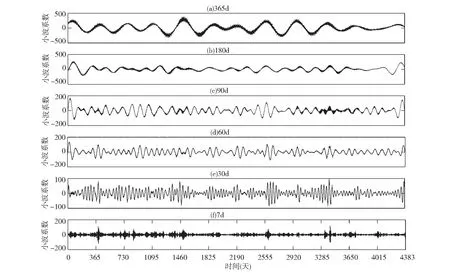
图5　不同时间尺度下污染指数的小波系数Fig.5　Wavelet coefficients of air pollution index in different time scales

图5所显示的12年来污染指数的逐日变化展现出周期性振荡规律，振幅的最大值均出现在年初和年末，而年中相对平缓，振幅越大，表明污染越严重，反之振幅越小，表明污染较轻。在图5(a)准1年(365d)的时间尺度上，振幅具体表现为“次高→高→低→次高→低”的变化特征：2001年～2003年振幅较高，2004年～2005年突然增高，2006年振幅相对平缓，2007～2009年振幅较高，2010年～2012年振幅平缓。在图5(b)准半年(180d)的时间尺度上，周期性振荡呈现出“高→次高→低→次高→低→次高→次低→高”的变化特征：2001年振幅高，2002年～2003年相对平缓，2004年振幅较高，2005年～2006年相对平缓，2007年～2010年振幅较高，2011年振幅最平缓，2012年又突然增高。在图5(c)准季节(90d)和图5(d) 2个月(60d)的时间尺度上，呈现出“高→次高→高”反复交替的波动特征，其共同点是年中比年末波动相对平缓。在图5(e) 1个月与图5(f) 1周的时间尺度上，“高→低”的波动频率表现得更为明显，最大值亦出现在年初和年末。可以看出，在365d的大时间尺度上，污染指数在近2年呈现出逐渐平缓的趋势；而聚焦到小尺度后，污染指数仍然波动强烈。

3.3PM10污染指数变化的周期与极值

运用小波方差分析来揭示波动变化的主周期是一种有效的方法，小波方差是一定尺度下表示时间序列中空气污染指数波动强弱及能量大小的参数，可以确定研究对象时间序列中各种尺度的波动强度及其随尺度的变化[20]。

图6　小波系数方差Fig.6　The variance of wavelet coefficients

时间序列中所包含的各种尺度的波动及其振幅大小都可以通过小波方差反映出来，在各种尺度的波动中，最大峰值处的时间尺度就是该时间序列的主要时间尺度，反映时间序列的主周期[10]，利用小波方差图，可以有效地找出一个时间序列中波动最强、起主要作用的周期。通过分析得出，拉萨市近12年逐日空气污染指数变化具有290d左右的主周期(图6)。分析其290d尺度上的小波系数来确定主周期的污染指数的变化规律，并由该尺度小波系数确定其极值，这样可以准确反映出极大值或极小值的出现时间(图7)。

从整体上看，以290d为时间尺度的小波系数波动情况呈现出“高→次高→低”的趋势，波动变化有明显的季节性特征。由图7可以看出：波峰大约都出现在每年的1月份左右，这表明每年12月～次年3月是拉萨市空气污染最严重的时期；波谷大约都出现在每年的8月份左右，这表明每年6月～10月是拉萨市空气污染最轻的时期。

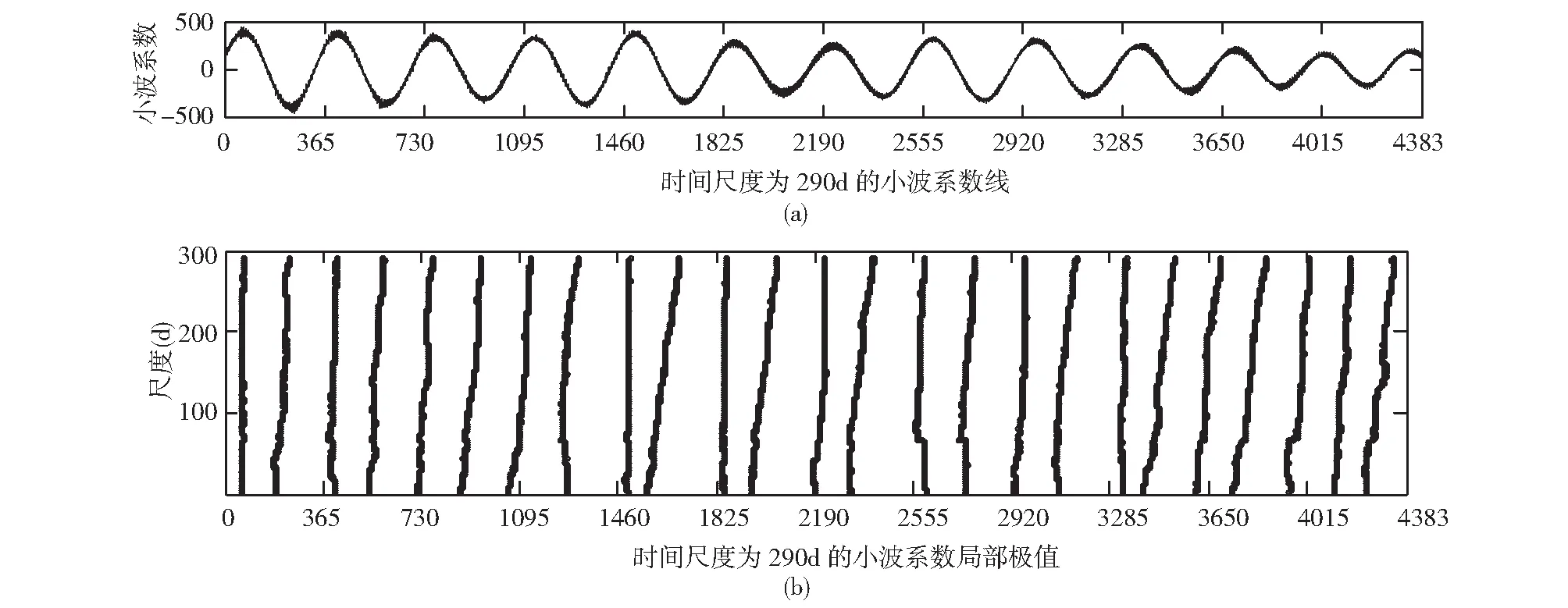
图7　时间尺度为290d的小波系数及局部极值Fig.7　Wavelet coefficient and the Local extremum of 290d time scale

4　讨　论

污染指数的多尺度变化研究可以服务于空气污染的未来短期监测，这对其污染的治理有较强的指导意义。拉萨市近12年的PM10污染指数的时间序列变化特征与兰州、重庆等城市的变化规律相似[7, 8]，这3个城市虽然地理位置和污染等级不同，但所处环境都为盆地河谷地形，污染指数均呈现出“冬重夏轻”的特征。拉萨市属于工业欠发达地区，受工业污染影响较小，所以影响其空气质量状况的因素主要与本区的自然环境和人为活动有关。拉萨市沙漠化严重，丰富的地表沙源以及干旱多风的气候是其沙尘天气形成的主要原因[21]，拉萨市地处喜马拉雅山脉北侧，受下沉气流的影响，由于海拔较高，全年多晴朗天气，降雨稀少，属高原温带半干旱季风气候，冬季寒冷干燥，多大风天气，这就易使干燥、疏松的地表形成扬沙、沙尘暴[22]。另外，由于冬季寒冷漫长，当地居民的取暖方式依然是以燃烧木材、煤炭等为主，而且缺乏良好的净化措施，这就人为地加重了冬季的污染情况[23, 24]。此外，随着拉萨市经济的发展以及人民生活水平的提高，机动车数量迅速增长，机动车尾气也是加剧空气中PM10形成的原因之一。拉萨河谷夏季多雨，降雨多集中在6～9月，根据西藏自治区气候中心发布的2012年气候变化监测公报，近年来西藏地区的降水量呈明显增长趋势，平均每10年增加6.6mm；沙尘暴天气明显减少；暖昼、暖夜指数呈显著上升趋势，增幅分别为6.7d/10年和11.4d/10年，而冷昼和冷夜指数呈明显的下降趋势，每10年分别下降5.1d和9.2d。中雨日数、大雨日数、连续湿日和极强降水量等6个极端降水指数均呈增加趋势。降水对空气中PM10污染物有很好的净化作用，这是拉萨市近年来空气污染指数呈减弱趋势的重要原因[22, 25]。此外，环保部门的积极努力以及人们污染防治意识的提高是治理城市空气污染必不可少的前提。本文研究的不足在于时间序列的长度还有待进一步增加，时间尺度越长，所获取的数据资料越多，越能探寻出污染指数的变化规律。这也是下一步研究的目标之一。

5　结　论

5.1利用Morlet小波分析拉萨市近12年的污染指数变化，得出其污染指数呈现出“冬重夏轻”的季节性变化。污染指数变化具有多尺度性，高峰期集中于12月～次年3月，通过小波方差计算出最大峰值处的时间尺度，得出其以290d左右为主周期。

5.2拉萨市空气污染指数在近几年有逐渐减弱的趋势，这主要与拉萨市近年来的气候变化有关，近年来降水日数的增多对降低空气中PM10含量具有重要作用，总体上拉萨市的空气污染情况正在好转。

5.3利用Morlet小波对时间序列进行时间、频率的局部化分解，展现污染指数变化的多尺度精细结构，对任意尺度上污染指数的阶段性及其周期和局部极值的特征进行分析，可以准确展现任意尺度污染指数的变化频率，利用小波分析来解读污染指数的时间序列变化对城市大气污染的监测和预报有很大参考价值。

[1]黄琼中. 拉萨市环境空气中NO_2变化特征分析[J]. 环境科学研究, 2006, 19(2):53-56,70.

[2]何晓红, 次仁德吉,林志强. 拉萨一次浮尘天气过程分析[J]. 气象, 2007, 33(9):69-73.

[3]董雪玲. 大气可吸入颗粒物对环境和人体健康的危害[J]. 资源·产业, 2004, 6(5):52-55.

[4]任阵海, 万本太, 苏福庆, 等. 当前我国大气环境质量的几个特征[J]. 环境科学研究, 2004, 17(1):1-6.

[5]张兴安, 拉萨被列为全国大气污染防治重点城市[N]. 西藏日报, 2013-4-18(02).

[6]李文杰, 张时煌, 高庆先, 等. 京津石三市空气污染指数(API)的时空分布特征及其与气象要素的关系[J]. 资源科学, 2012, 34(8):1392-1400.

[7]王海鹏, 张斌, 刘祖涵, 等. 基于小波变换的兰州市近十年空气污染指数变化[J]. 环境科学学报, 2011, 31(5):1070-1076.

[8]孙高敏, 许武成, 周杜辉, 等. 重庆市近11年空气污染指数变化的小波变换分析[J]. 后勤工程学院学报, 2012, 28(2):70-75.

[9]柴微涛, 宋述军,宋学鸿. 成都市城区空气污染指数的时间序列分析[J]. 成都理工大学学报(自然科学版), 2007, 34(4):485-488.

[10]吴小玲, 张斌, 艾南山, 等. 基于小波变换的上海市近10年SO2污染指数的变化[J]. 环境科学, 2009, 30(8):2193-2198.

[11]Zolghadri A, Henry D. Minimax statistical models for air pollution time series. Application to ozone time series data measured in Bordeaux[J]. Environmental Monitoring and Assessment, 2004, 98(1-3):275-294.

[12]Harri Niska, Teri Hiltunen, Ari Karppinen, et al. Evolving the neural network model for forecasting air pollution time series[J]. Engineering Applications of Artificial Intelligence, 2004, 17(2):159-167.

[13]Shi Kai, Liu Chun-qiong, Ai Nan-shan, et al. Using three methods to investigate time-scaling properties in air pollution indexes time series[J]. Nonlinear Analysis: Real World Applications, 2008, 9(2):693-707.

[14]周顺武,黄琼中. 拉萨市空气污染物浓度的统计分析及其可能的天气原因[J]. 西藏科技, 2002, 1(5):39-42.

[15]平措,尤学一. 拉萨城市大气污染现状及防治对策[J]. 干旱区资源与环境, 2005, 19(7):106-109.

[16]黄琼中. 拉萨市环境空气质量与气象特征分析[J]. 中国环境监测, 2001, 17(6):50-53.

[17]卓嘎, 德庆卓嘎,陈涛. 拉萨市大气污染分布特征及气象影响因子分析[J]. 中国环境监测, 2009, 25(1):90-97,40.

[18]徐建华. 现代地理学中的数学方法[M], 高等教育出版社, 2002.

[19]胡昌华. 基于 MATLAB 的系统分析与设计: 小波分析[M]. 西安电子科技大学出版社, 1999.

[20]许月卿, 李双成,蔡运龙. 基于小波分析的河北平原降水变化规律研究[J]. 中国科学(D辑:地球科学), 2004, 34(12):1176-1183.

[21]沈渭寿,杨萍. 西藏拉萨市土地沙漠化现状与趋势[J]. 中国沙漠, 1999, 19(1):34-38.

[22]罗布次仁, 晓柏,巫鹏飞. 近几年拉萨市环境空气质量状况及与部分气象要素的关系分析[J]. 西藏科技, 2007, 1(9):52-55.

[23]李向阳, 丁晓妹, 高宏, 等. 中国北方典型城市API特征分析[J]. 干旱区资源与环境, 2011, 25(3):96-101.

[24]平措. 西藏拉萨市城市空气污染管理现状及其思考[J]. 西藏大学学报(自然科学版), 2012, (1):7-10.

[25]董继元, 王式功,尚可政. 降水对中国部分城市空气质量的影响分析[J]. 干旱区资源与环境, 2009, 23(12):43-48.

Wavelet Analysis on Pollution Index Changes of Lhasa in Recent 12 Years

WANG Lei, DENG Qing-chun, LIU Hui, ZHANG Zheng-ling,LI Xiang

(SchoolofLand&Resources,ChinaWestNormalUniversity,Nanchong,Sichuan637000,China)

As a typical plateau city, studying the air pollution changes of Lhasa has a great significance to other plateau cities. Based on the time series of daily pollution index during 2001 to 2012 of Lhasa city, the one-dimensional continuous Morlet wavelet transform was analysed. The results showed thatthe variations of PM10pollution index in different time scales of Lhasa City presented high in winter and low in summer. The peak of pollution was between December and next March, and concentrated precipitation in summer has a good function of cleaning the PM10pollutants in the air. The air pollution index variations in different time scales were analyzed. The main fluctuation period is about 290 days, and fluctuation range was gradually weakening.

Air pollution index; PM10；wavelet analysis; Lhasa city;

2014-10-09

王磊(1992-)，男，陕西西安人，西华师范大学国土资源学院水土保持与荒漠化防治专业2013级在读硕士研究生，主要研究方向为环境地理。

邓青春,qingqing123ok@163.com。

X823

A

1001-3644(2015)02-0052-07