基于DEM模拟气固鼓泡床中颗粒碰撞参数对流场间歇性的影响

彭丽，吴迎亚，李佳瑶，高金森，蓝兴英

（中国石油大学（北京）重质油国家重点实验室，北京 102249）

引 言

鼓泡床具有良好的传热和传质特点，在化学工程、生物环境工程以及食品加工方面有着广泛的应用[1]。计算流体力学方法（CFD）[2-3]常用于研究鼓泡床的流动行为[4]，其中基于欧拉-拉格朗日的CFD-DEM 方法常用于模拟追踪颗粒相的运动，该方法可以从单颗粒层面上研究颗粒间的碰撞过程和气体-颗粒间的相互作用过程，从而能够更加准确地模拟出整个床层的气固流动过程，所以DEM 方法是研究鼓泡床内微观机制的重要方法。目前，DEM方法主要采用软球模型处理颗粒间接触、变形、受力和运动，将颗粒的碰撞视为弹簧-阻尼系统[5-8]，分别采用颗粒弹性系数（k）和颗粒恢复系数（e）描述颗粒碰撞作用力和碰撞过程中的能量损失。因此，在气固鼓泡床流动的CFD-DEM 模拟中这两个参数是影响模拟结果的关键参数。已有的实验和模拟研究表明，鼓泡床内颗粒运动并非是完全无规则的运动，存在着大量的有序运动，这种有序运动被称为相干结构，具体表现为颗粒涡团[9]，这种相干结构从微观上表征颗粒速度脉动的生成与发展。Sun 等[10]和Jiradilok 等[11]指出正是由于相干结构的存在引起了流场间歇性，即颗粒涡团在时空中的不均匀出现或变化。因此，流场相干结构和间歇性均反映了鼓泡床内气固流动的微观特性。已有的研究主要是从宏观角度[12-16]研究颗粒碰撞属性对鼓泡床气固流动的影响，很少从微观角度进行分析。但鼓泡床内气固运动的微观特性对传热和传质有着重要的影响，因此本研究重点考察了颗粒碰撞属性对流场相干结构和间歇性等微观行为的影响，为找到一个准确模拟气固鼓泡流动行为的方法提供依据。有研究者在研究湍流相干结构时引入了小波分析方法，发现小波分析能在多个尺度上剖析湍流的相干结构[17]。前期本课题组已应用CFD-DEM 方法对气固鼓泡床内气固流动进行了模拟研究，并利用小波分析方法分析了床层内的多尺度相干结构[18]。本研究在前期工作基础上分析CFD-DEM 方法中的关键参数——颗粒弹性系数和恢复系数对鼓泡床气固流动行为的影响，并利用小波分析方法剖析颗粒弹性系数和恢复系数对鼓泡床内流场间歇性和相干结构的影响。

1 模拟对象

本研究的模拟工况为Goldschmidt 等[19]的拟二维鼓泡床冷态实验，计算模型如图1所示。气体从底部均匀进气，速度入口，无分布板；气体出口采用压力出口。具体的实验条件及相关模拟参数见表1。

图1 计算模型的几何结构Fig.1 Geometry structure of simulation domain

2 数学模型

2.1 CFD-DEM 模型

本研究采用 MFIX 软件（开源代码：https://mfix.netl.doe.gov/），基于欧拉-拉格朗日的CFD-DEM 模型对鼓泡床内气固流动过程进行模拟研究。该模型通过跟踪流场中每一个颗粒的运动轨迹来模拟整个流场中颗粒运动。采用Gidaspow 曳力模型[20]描述气-固相两相作用力。气相采用层流模型。颗粒相的碰撞采用软球模型[21-22]描述，将颗粒碰撞视为非弹性碰撞，并考虑摩擦力的存在。关于模型的详细描述及相关表达式见文献[19]。

表1 模拟条件Table 1 Simulation conditions

2.2 小波分析方法

函数f(t)在小波基函数φ(t)的连续小波变换定义为f(t)在φ(t)时的卷积[23]

式中，ϕab(t) 是 ϕ(t) 经过平移变换和伸缩变换得到的一系列小波族函数，目前常用的小波基函数有墨西哥帽、法兰西帽、Morlet 函数和Daubechies函数等[24]。小波变换不仅能表达频域信息，还能表达时域信息，具有时频双局部化的能力。为了定量分析鼓泡床中颗粒涡等相干结构，小波变换是一种很有效的工具，这一点已经在单相湍流上得到了证实[25]。一般分析湍流信息时小波基函数采用Daubechies 函数，所以本研究中采用Daubechies 函数为小波基函数分析鼓泡床中相干结构。

3 结果与讨论

3.1 颗粒弹性系数和恢复系数对鼓泡床流场间歇性的影响

Maxwell 曾指出[26]，采用DEM 方法模拟气固鼓泡流化床时，颗粒弹性系数k一般取400～1500 N·m-1，颗粒恢复系数e一般取0.8～1.0。目前，在气固流化床模拟中k和e一般设为常数[27]，k和e取值的不同会影响床层中颗粒脉动，从而影响整个流场的间歇性。本研究考察了e=0.90 时，k分别为400、800、1000、1200、1500 N·m-1，以及k=1000 N·m-1时，e分别为0.80、0.90、0.95、0.99 时鼓泡床的气固流动行为。

在鼓泡床中，颗粒速度脉动能和平均床层高度反映了颗粒在碰撞过程中能量的变化，也间接反映出流场的间歇性。鼓泡床的瞬时颗粒平均高度反映了床层随时间的波动特性。瞬时颗粒平均高度计算公式如下

式中，n是颗粒数目，hk是k颗粒的瞬时高度。

图2和图3分别为颗粒在床中心处（X=7.5 cm，Y=7.5 cm）Y方向上的瞬时速度（颗粒速度）脉动能随弹性系数和恢复系数的变化情况。由图2可知，随着弹性系数的增大，在鼓泡床低频高能区能谱曲线呈上升趋势；但在高频耗散区，k为1200、800 N·m-1时的能量高于k为1000 N·m-1时的能量，能谱曲线偏离了Kolmogorov-5/3 的标度律[28]，说明颗粒流场中存在着引起流场间歇性的相干结构。由图3可知，在高频耗散区，随着颗粒恢复系数的增大，碰撞过程中的能量损耗降低。

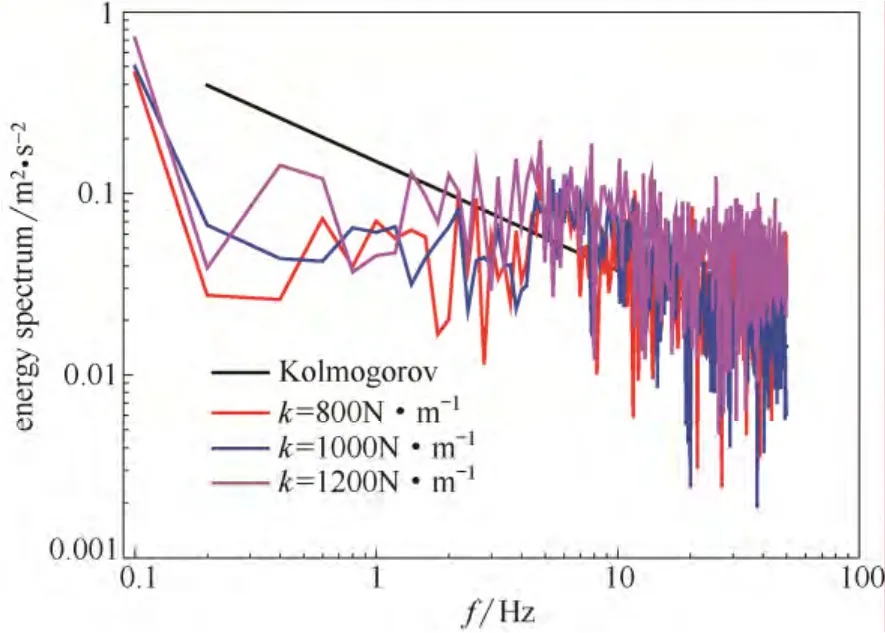
图2 不同弹性系数下颗粒速度脉动能谱图Fig.2 Fluctuating energy spectrum of particle velocity at different elasticity coefficients (e=0.90)

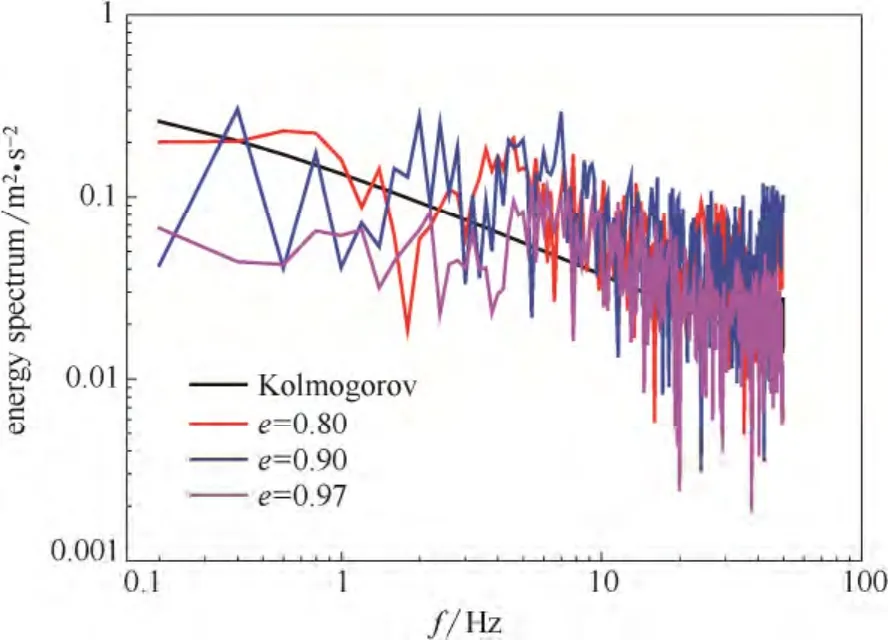
图3 不同恢复系数下颗粒速度脉动能谱图Fig.3 Fluctuating energy spectrum of particle velocity at different restitution coefficients (k=1000 N·m-1)

颗粒碰撞过程中的能量变化会引起平均床层高度的变化，图4和图5给出了床层高度随弹性系数和恢复系数的变化情况。如图4所示，k为1000 N·m-1时平均床层高度最高，对应图2中显示的耗能区能量最低。图5显示，随着恢复系数的增大，高频区颗粒速度脉动能损耗降低，床层高度增高。

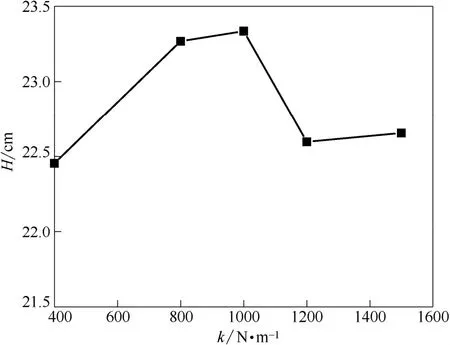
图4 颗粒弹性系数对平均床层高度的影响Fig.4 Effect of elasticity coefficients on mean bed height (e=0.90)

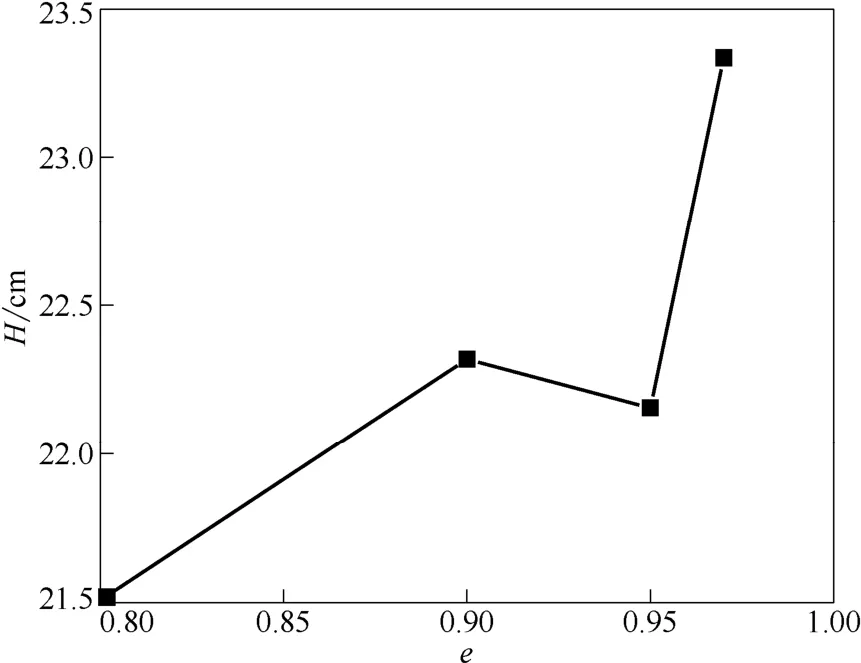
图5 颗粒恢复系数对平均床层高度的影响Fig.5 Effect of restitution coefficients on mean bed height (k=1000 N·m-1)

上述颗粒速度脉动能谱分析表明颗粒流场存在较强的间歇性，但是速度脉动能谱图无法量化流场间歇性的强弱。类似于单相湍流的流场间歇性的 量化指标[18]，前期工作已表明采用平坦因子FF 可以定量描述鼓泡床流场间歇性的强度[29]。对于颗粒的脉动速度，其FF 定义为

式中，v(x) 表示颗粒在Y方向上的脉动速度，表示求平均。当FF＜3，表明颗粒的脉动速度存在较强的周期性；当FF=3，表明颗粒流场不存在间歇结构，颗粒速度脉动是由于随机脉动造成的；当FF＞3，表明颗粒的脉动速度存在间歇性，而且FF 越大流场的间歇性越强。

为此，本研究进一步通过平坦因子定量分析颗粒弹性系数和恢复系数对流场间歇性的影响。图6和图7分别为平坦因子随弹性系数和恢复系数的变化情况。如图所示，在不同的k和e时FF 均大于3，说明鼓泡床内流场存在较强的间歇性。随着k的 增大，平坦因子先降低后增加，当k增大到1000 N·m-1时平坦因子最小，反映了流场间歇性最弱，整体能量耗散最低，对应床层最高，这与图2、图4的分析结果一致。随着e取值的增大，颗粒在动量传递过程中的能量损耗降低，导致颗粒速度脉动能降低，流场间歇性也降低，床层高度增加，这也与图3、图5的分析结果一致。

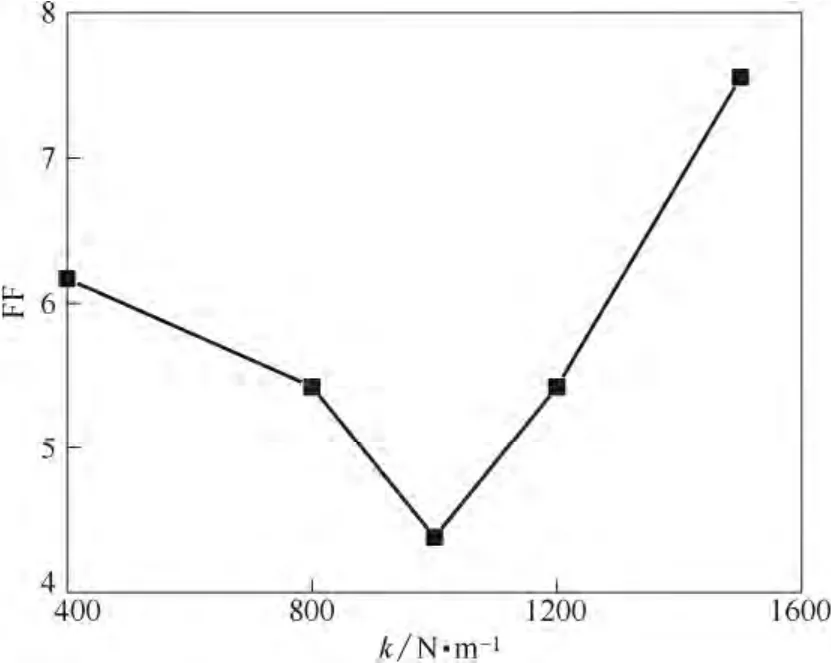
图6 不同颗粒弹性系数对平坦因子FF 的影响Fig.6 Effect of elasticity coefficients on flatness factor (e=0.90)

图7 不同颗粒恢复系数对平坦因子FF 的影响Fig.7 Effect of restitution coefficients on flatness factor (k=1000 N·m-1)

3.2 颗粒弹性系数和恢复系数对鼓泡床内相干结构的影响

采用小波变换分析方法[30-31]进一步研究了颗粒弹性系数和恢复系数对鼓泡床流场间歇性以及相干结构的影响。图8和图9分别为不同弹性系数和恢复系数下H为18 cm 截面处的平坦因子与频率之间的关系。由图可知，在低频区FF 较低，说明低频区流场的间歇性较弱，流场的相干结构少。随着弹性系数的增大，在高频区k为1000 N·m-1时出现了一个极小值；随着恢复系数的增大，在高频区FF 变小，流场的间歇性变化规律与3.1 节的分析一致。根据单相湍流理论，类比于大涡模拟，将鼓泡床颗粒湍动区域分为大涡和小涡，大涡区对应低频区，小涡区对应高频区。由于整个颗粒的能量主要集中在大涡区，能量高，大涡在时间和空间上的分布比较均匀，间歇性较弱，不会产生相干性结构；在小涡区，FF 明显大于3，小涡的不断扰动存在着大量的相干结构，造成了流场较强的间歇性。

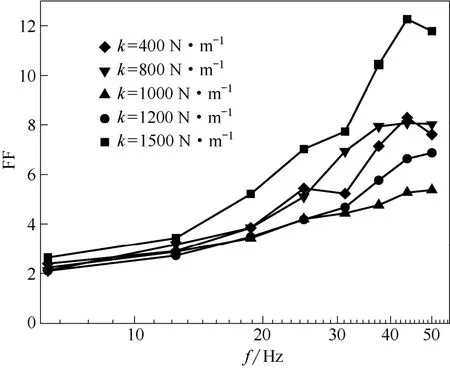
图8 不同弹性系数的平坦因子与频率之间的关系Fig.8 Effect of frequency on flatness factor at different elasticity coefficients (e=0.90,H=18 cm)

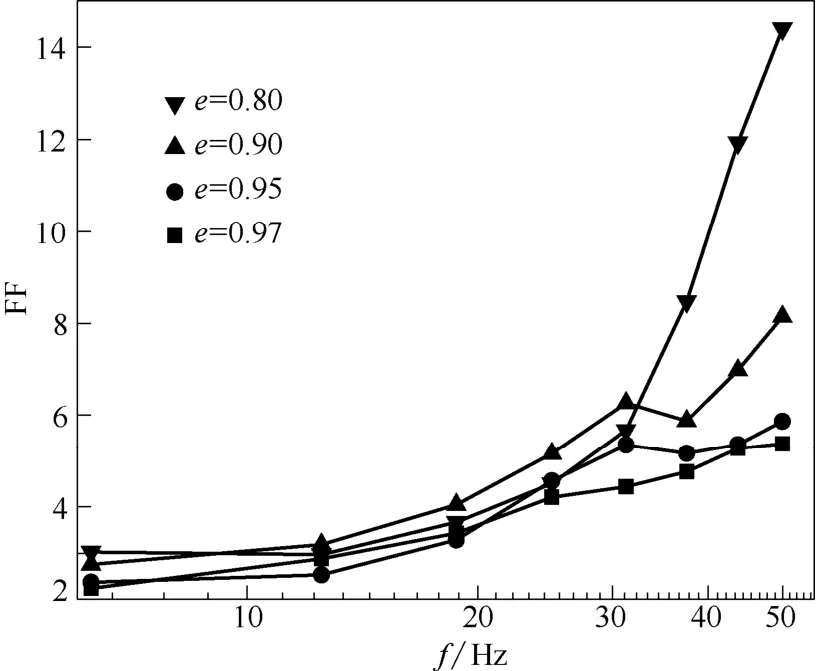
图9 不同恢复系数的平坦因子与频率之间的关系Fig.9 Effect of frequency on flatness factor at different restitution coefficients (k=1000 N·m-1，H=18 cm)

进一步分析了颗粒弹性系数和恢复系数对小波系数的概率密度函数（PDF）分布的影响。Onorato等[32]指出小波系数的PDF 拖尾长度可以表示为相干结构引起的流场间歇性的强弱。如图10所示，k为1000 N·m-1时主峰较强，拖尾较弱，说明k为1000 N·m-1时流场间歇性较弱。由图11可以看出，随着恢复系数的增大，小波系数的主峰增高，拖尾减小，进一步说明恢复系数的增大降低了流场的间歇性。

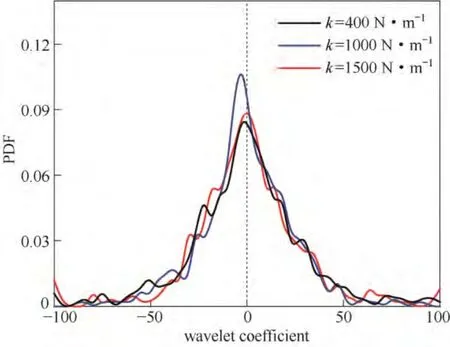
图10 不同弹性系数下小波系数的PDF 分布Fig.10 Probability density function of wavelet coefficient at different elasticity coefficients (e=0.90)

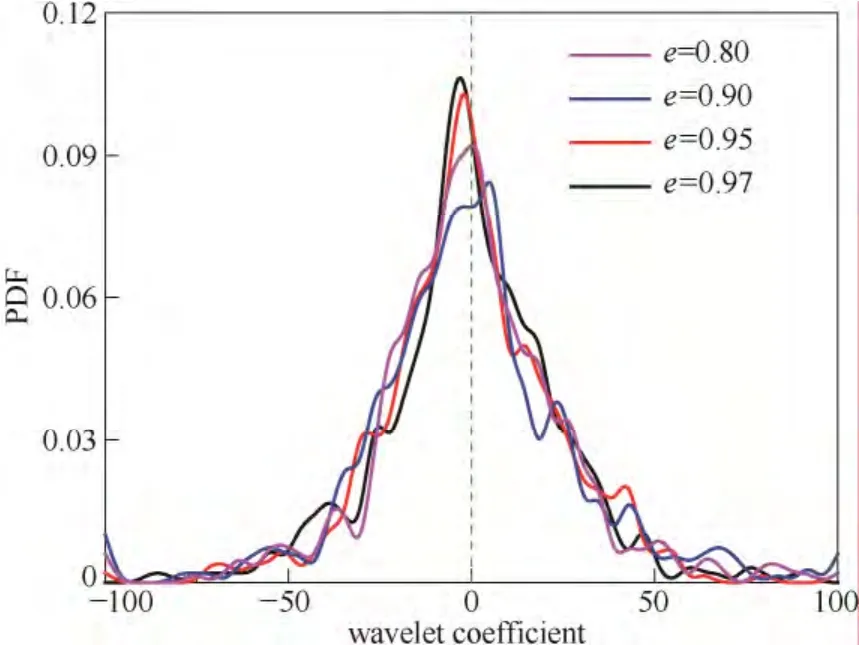
图11 不同恢复系数下小波系数的PDF 分布Fig.11 Probability density function of wavelet coefficient at different restitution coefficients (k=1000 N·m-1)

3.3 颗粒弹性系数和恢复系数对流场相干结构的多尺度的影响

进一步考察了颗粒弹性系数和恢复系数对流场相干结构的多尺度的影响。图12和图13为不同弹性系数和恢复系数下不同小波分解尺度下小波系数的相干平面图，以可视化的方式显示出了在不同弹性系数和恢复系数下颗粒涡团随时间的演化过程。由图可以看出，在涡的中心处相干性最强，相邻涡团之间相关性最弱的是两个涡的分界线[33]；鼓泡床中相干结构往往不止一个，大尺度涡和小尺度涡并存，沿着时间的历程某些尺度的涡会呈现周期性特征，并伴随着与相邻尺度涡的合并和分解，说明该时间段内相干涡与邻近尺度涡存在着强烈的相互作用，导致了涡的聚并和破碎[34]。由图12可知，在小波尺度为0～20 时，随着弹性系数的增大，涡中心数目基本一致，这是由于该尺度下相干结构（涡）主要由背景湍流造成。随着小波尺度的增加，涡团的数目逐渐减少。在60～128 尺度下，涡团的数目急剧减少，但涡的强度大、范围广，大涡分解成一部分小涡。在小波尺度为40 左右，随着弹性系数的增大，涡中心数目先降低后增加，说明流场间歇性先降低后增加，这与图6平坦因子随弹性系数先降低后增大的变化趋势一致。由图13可知，在小波尺度为0～20 时，随着恢复系数的增大，涡中心数目基本一致。随着小波尺度的增加，涡团数目逐渐减少。在60～128 尺度下，涡团的数目也急剧减少，大涡会分解成一部分小涡。在小波尺度为40左右，随着恢复系数的增大，涡中心数目呈下降的趋势，说明流场间歇性下降，这与图7平坦因子随恢复系数增大而降低的分析一致。

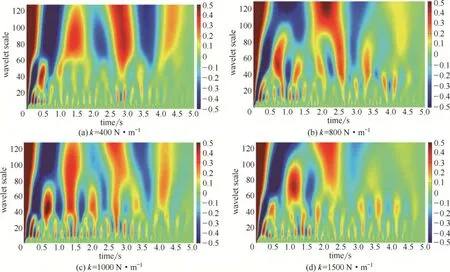
图12 不同弹性系数下的小波系数自相关平面图Fig.12 Auto-correlation of wavelet in different elasticity coefficients (e=0.90)

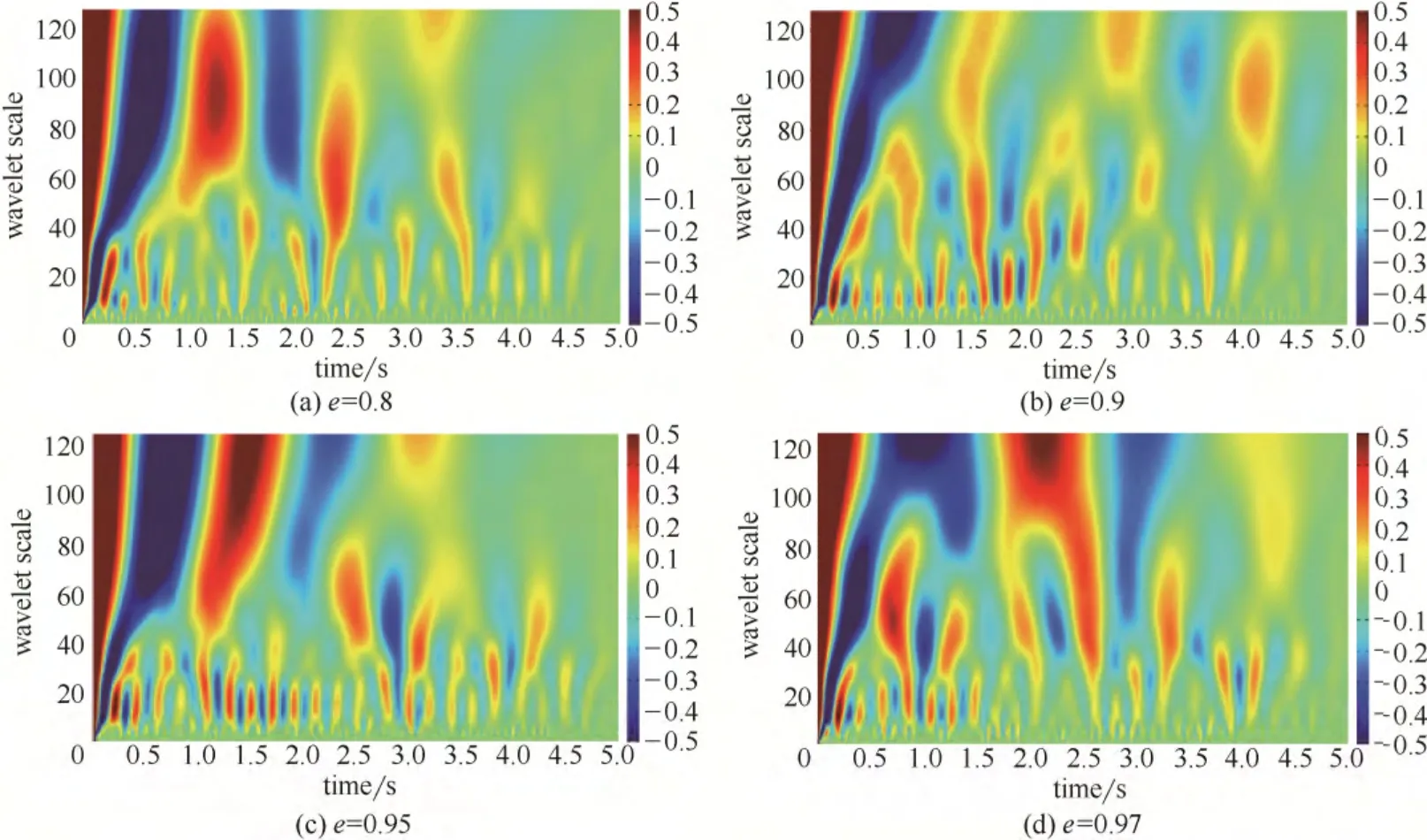
图13 不同恢复系数下的小波系数自相关平面图Fig.13 Auto-correlation of wavelet in different restitution coefficients (k=1000 N·m-1)

4 结 论

本研究采用DEM 方法对鼓泡床内气固流动过程进行了模拟研究，重点分析了颗粒弹性系数和恢复系数对鼓泡床流场间歇性的影响，并利用小波变化方法分析了弹性系数和恢复系数对鼓泡床内相干结构的影响，得到以下结论。

（1）颗粒弹性系数和恢复系数对颗粒速度脉动能、平均床层高度以及平坦因子有一定影响。随着颗粒弹性系数取值的变大，高频区能量和平坦因子先降低后增加，床层高度先增加后降低，流场间歇性先减弱后增强。在k为1000 N·m-1时，高频区能量和平坦因子最低，床层高度最大，对应流场间歇性最弱。颗粒恢复系数越大，高能区能量和平坦因子越低，床层高度越大，流场间歇性越弱。

（2）颗粒弹性系数和恢复系数对小波系数的概率密度函数有一定影响。在k为1000 N·m-1时，主峰较强，拖尾较弱，流场间歇性较弱。随着恢复系数的增大，小波系数的主峰增强，拖尾减弱，流场间歇性减弱。

（3）颗粒弹性系数和恢复系数对颗粒流场中引起流场间歇性的颗粒涡团有显著的影响。在高频区小波尺度为40 附近，随着弹性系数的增大，涡中心数目先减少后增加，进一步说明流场间歇性先减弱后增强；随着恢复系数的增大，涡中心数目逐渐减少，流场间歇性逐渐减弱。本研究结果表明，在DEM 方法中颗粒碰撞参数的取值对气固鼓泡床流场间歇性有较大的影响，针对不同体系选择合适的颗粒碰撞参数可为更加准确地模拟鼓泡床气固流动现象提供基础。

[1]Jin Yong (金涌),Zhu Jingxu (祝京旭),Yu Zhiqing (俞芷青).Fluidization Engineering Principles (流态化工程原理) [M].Beijing:Tsinghua University Press,2001:72-75.

[2]Cundall P A,Strack O D L.A discrete numerical model for granular assemblies [J].Otechnique,1997,29 (1):331-336.

[3]Zhu H P,Zhou Z Y,Yang R Y,et al.Discrete particle simulation of particulate systems:a review of major applications and findings [J].Chemical Engineering Science,2008,63 (23):5728-5770.

[4]Enwald H,Peirano E,Almstedt A E.Eulerian two-phase flow theory applied to fluidization [J].Ⅰnternational Journal of Multiphase Flow,1996,22:21-66.

[5]Tsuji Y,Kawaguchi T,Tanaka T.Discrete particle simulation of two-dimensional fluidized bed [J].Powder Technology,1993,77 (1):79-87.

[6]Kawaguchi T,Tanaka T,Tsuji Y.Numerical simulation of two-dimensional fluidized beds using the discrete element method (comparison between the two- and three-dimensional models) [J].Powder Technology,1998,96 (2):129-138.

[7]Feng Y Q,Yu A B.Assessment of model formulations in the discrete particle simulation of gas-solid flow [J].Ⅰndustrial & Engineering Chemistry Research,2004,43 (26):8378-8390.

[8]Pandit J K,Wang X S,Rhodes M J.Study of Geldart’s Group A behaviour using the discrete element method simulation [J].Powder Technology,2005,160 (1):7-14.

[9]Sun J,Wang J,Yang Y.CFD simulation and wavelet transform analysis of vortex and coherent structure in a gas-solid fluidized bed [J].Chemical Engineering Science,2012,71 (26):507-519.

[10]Sun J,Wang J,Yang Y.CFD investigation of particle fluctuation characteristics of bidisperse mixture in a gas-solid fluidized bed [J].Chemical Engineering Science,2012,82 (12):285-298.

[11]Jiradilok V,Gidaspow D,Breault R W.Computation of gas and solid dispersion coefficients in turbulent risers and bubbling beds [J].Chemical Engineering Science,2007,62 (13):3397-3409.

[12]Fang Mingming (房明明),Luo Kun (罗坤),Yang Shiliang (杨世亮),Zhang Ke (张科),Fan Jianren (樊建人).CFD-DEM investigation and parameter sensitivity analysis of a typical bubbling fluidization process [J].Journal of Engineering Thermophysics(工程热物理学报),2013,34 (6):1106-1111.

[13]Navarro H A,de Souza Braun M P.Determination of the normal spring stiffness coefficient in the linear spring-dashpot contact model of discrete element method [J].Powder Technology,2013,246:707-722.

[14]Kharaz A H,Gorham D A,Salman A D.An experimental study of the elastic rebound of spheres [J].Powder Technology,2001,120 (3):281-291.

[15]Fu J S,Cheong Y S,Reynolds G K,et al.An experimental study of the variability in the properties and quality of wet granules [J].Powder Technology,2004,140 (3):209-216.

[16]Müller P,Antonyuk S,Tomas J,et al.Investigations of the Restitution Coefficient of Granules—Micro-Macro-Interaction [M].Berlin:Springer,2008:235-241.

[17]Xia Zhenyan (夏振炎),Tian Yan (田砚),Jiang Nan (姜楠).Wavelet spectrum analysis on energy transfer of multi-scale structures in wall turbulence [J].Applied Mathematics and Mechanics(应用数学和力学),2009,30 (4):409-416.

[18]Wu Yingya (吴迎亚),Lan Xingying (蓝兴英),Gao Jinsen (高金森).Analysis of flow field intermittency and coherent structure of particles based on DEM simulation of gas-solid bubbling bed [J].CⅠESC Journal(化工学报),2014,65 (7):2724-2732.

[19]Goldschmidt M J V,Beetstra R,Kuipers J A M.Hydrodynamic modelling of dense gas-fluidised beds:comparison and validation of 3D discrete particle and continuum models [J].Powder Technology,2004,142 (1):23-47.

[20]Gidaspow D.Multiphase Flow and Fluidization:Continuum and Kinetic Theory Descriptions [M].Boston:Academic Press,1994.

[21]Zhang Yong (张勇),Jin Baoshen (金保升),Zhong Wenqi (钟文琪).Three-dimensional DEM simulation on particle mixing characteristics of spout-fluid bed [J].Proceedings of the CSEE(中国电机工程学报),2008,28 (2):33-38.

[22]Sommerfeld M,Tsuji Y,Crowe C T.Multiphase Flows with Droplets and Particles [M].Boca Raton:CRC Press,1997:12-14.

[23]Wang Jiajun (王嘉骏),Zhang Wenfeng (张文峰),Feng Lianfang (冯连芳),Gu Xueping (顾雪萍).Wavelets analysis of pressure fluctuation in agitated fluidized bed [J].Journal of Chemical Ⅰndustry and Engineering(China) (化工学报),2006,57 (12):2855-2859.

[24]Mallat S G.A theory for multiresolution signal decomposition:the wavelet representation [J].Pattern Analysis and Machine Ⅰntelligence,ⅠEEE Transactions on,1989,11 (7):674-693.

[25]Giri B K,Mitra C,Panigrahi P K,et al.Multi-scale dynamics of glow discharge plasma through wavelets:self-similar behavior to neutral turbulence and dissipation [OL].[2014-01-13].http://arxiv.org/abs/ 1401.2742.

[26]Zhang Ke (张科).CFD-DEM simulation of complex dense gas-solid flow [D].Hangzhou:Zhejiang University,2012.

[27]Tian F G,Zhang M C,Fan H J,et al.Numerical study on microscopic mixing characteristics in fluidized bedsviaDEM [J].Fuel Process Technology,2007,88 (2):187-198.

[28]Tamburini A,Cipollina A,Micale G,et al.CFD simulations of dense solid-liquid suspensions in baffled stirred tanks:prediction of solid particle distribution [J].Chemical Engineering Journal,2013,223:875-890.

[29]Jiang Nan (姜楠),Tian Yan (田砚).Wavelet analysis of detecting multi-scale coherent structures and intermittency in wall turbulence [J].Journal of Harbin Engineering University(哈尔滨工程大学学报),2005,26 (1):7-12.

[30]Liu Haifeng (刘海峰),Wu Tao (吴韬),Wang Fuchen (王辅臣),Gong Xin (龚欣),Yu Zunhong (于遵宏).Coherent structure of turbulence based on wavelet analysis (Ⅰ):Determining coherent structure with energy maxima criterion [J].Journal of Chemical Ⅰndustry and Engineering(China) (化工学报),2000,51 (6):761-765.

[31]Liu Haifeng (刘海峰),Zhao Tiejun (赵铁钧),Wang Fuchen (王辅臣),Gong Xin (龚欣),Yu Zunhong (于遵宏).Coherent structure of turbulence based on wavelet analysis (Ⅱ) :Wave shape and local singularity of coherent structure [J].Journal of Chemical Ⅰndustry and Engineering(China) (化工学报),2000,51 (6):766-770.

[32]Onorato M,Camussi R,Iuso G.Small scale intermittency and bursting in a turbulent channel flow [J].Physical Review E,2000,61 (2):1447.

[33]Zhang Bin (张斌),Wang Tong (王彤),Gu Chuangang (谷传纲),Dai Zhengyuan (戴正元).Identification of turbulent coherent structures based on wavelet and bi-spectrum analysis [J].Transactions of the Chinese Society for Agricultural Machinery(农业机械学报),2009,40 (11):203-207.

[34]Oberleithner K,Sieber M,Nayeri C N,et al.Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown:stability analysis and empirical mode construction [J].Journal of Fluid Mechanics,2011,679 (1):383-414.