水引射蒸汽引射器的数值模拟
屈晓航 睢 辉 田茂诚 房 达
(1.山东大学能源与动力工程学院,250061;2.济南市规划设计研究院:山东 济南250101)
引射器因没有运动部件而具有较高的可靠性,近年来对其在安全系统、余热回收方面应用的研究越来越多[1-3]。单相引射器中工质不发生相变,在引射式制冷和航天器试车台方面广泛应用[4-5]。两相引射器中工质发生相变,例如动力循环中的引射式低压加热器,因其能提高循环效率而受到越来越多的关注[6-8]。
诸多学者对两相引射器的性能进行了理论分析或实验研究,得到了引射器的引射系数、升温能力等受其结构和工作条件的影响规律[9-11];一些学者还研究了引射器性能对整个系统的影响规律。数值计算相比实验成本低,且能获得实验难以测量的内部流场、温度压力场等信息,但因两相流流动和传热的复杂性,两相引射器的数值计算还较少,计算准确性也难以保证。以欧拉-欧拉模型为基础,Shah和Gulawani分别利用Fluent和CFX建立数值模型对蒸汽引射水和蒸汽射流在水中的冷凝进行了数值计算[12-13]。
严俊杰提出采用较高压力的水引射蒸汽的方法回收低压蒸汽余热,并考察了水、蒸汽参数和引射器结构参数对回收余热蒸汽效果的影响[14-15]。本文以欧拉-欧拉模型为基础,使用Fluent建立水引射蒸汽引射器的数值计算模型,以期辅助水-蒸汽引射器的设计,并对两相流的数值计算有一定参考价值。
1 数值模型
1.1 欧拉-欧拉模型
采用欧拉-欧拉双流体模型,该模型为多相流中的每相分配单独的体积分数方程、连续性方程、动量方程和能量方程,方程具体形式如下:




式中,Vq、φq、ρq、、Sq、τq、hq分别为第q相的总体积、体积分数、密度、速度、质量源项、切应力和焓,mpq、mqp、hpq、hqp、分别为相间质量传递项、相间能量传递项、外体积力、升力、虚拟质量力、相间动量传递项、热流和能量源项。
1.2 冷凝模型
基于以上欧拉模型,数值计算中使用了基于热平衡原理的冷凝模型,Shah使用该模型对蒸汽引射水引射器进行计算,得到了令人满意的结果[12]。
该模型作如下假设:1)蒸汽冷凝只发生在气液界面上,蒸汽不发生雾化,气液界面的温度为当地压力对应的蒸汽饱和温度;2)气液界面显热传递量的差即认为由冷凝导致的潜热传递引起;3)蒸汽为副相,认为蒸汽冷凝是若干微小球形气泡的冷凝,这是欧拉模型的基本假设。
蒸汽泡直径dv在欧拉模型中用于计算拽力系数,同时在冷凝模型中用以计算雷诺数和努赛尔数,其分布是过冷度的函数[16]:
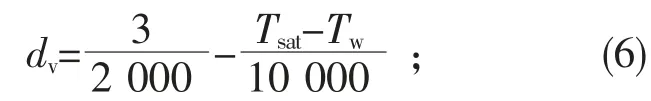
在球形假设下,单位体积内的气液传热面积即:

其中,下标w表示水,下标v表示蒸汽。气泡努赛尔数、雷诺数和普朗特数分别定义如下:

水侧的对流换热系数,使用Hughmark提出的关联式计算[17]:

汽侧的对流换热系数远大于液侧,该换热系数只要足够大就不会对计算结果产生影响,此处取为一个常数:

由热平衡可知,气液两侧热量传递量相等,气液界面显热传递量的差即认为由冷凝导致的潜热传递引起,于是单位时间单位体积内蒸汽冷凝量即为:

其中Hvw为当地压力下水蒸汽的气化潜热。
使用Fluent用户自定义函数(UDF)将冷凝模型代码加入到计算中。
1.3 计算区域和方法
计算的引射器结构如图1(a)所示,一次流为水,中心进水(图中A处),二次流为蒸汽,环周进汽(图中B处),压力较高的冷水引射低压饱和蒸汽。2者在引射器混合室内直接接触,蒸汽发生冷凝,水的温度升高,经喉部和扩压室升压后克服引射器背压(back pressure)排出(由图中C处)。引射器网格划分情况如图1(b)所示,采用六面体结构化网格,网格总数约为70×103。

图1 计算区域及网格划分(单位:mm)Fig 1 Calculation region and meshing(unit:mm)
计算过程中水为主相,蒸汽为副相。为保证计算的稳定性,所有方程的离散格式选为1阶格式或标准格式,采用压力速度的耦合SIMPLE算法,所有方程的松弛因子设为0.1或以下的数值。引射器进出口均采用压力边界条件,其中二次流入口蒸汽为对应压力下的饱和蒸汽。计算过程对进出口3个质量流量以及出口水温度进行监视,这4个参数均不再变化时认为迭代收敛。采用3维双精度稳态求解器,每种计算工况约需迭代5×104步,使用2GH单核,4GBRAM计算机,每种工况计算约需24 h。
2 结果分析
2.1 汽水分布
引射器中汽水分布的数值计算结果如图2所示,其中p(压力)和T(温度)的下标p、s和b分别代表引射器的一次流、二次流和出口。

图2 引射器中的水蒸汽分布云Fig 2 Distribution cloud of steam-water in the ejector
从图2可以看出,冷水从一次流喷嘴喷出后,保持和喷嘴出口相同直径的柱状,由于一次流对二次流的剪切作用和喷嘴出口较低的压力,蒸汽被引入,水继续在引射器中心流动而蒸汽在包围水柱的环形空间内流动,同时蒸汽在气液界面上冷凝,到达引射器扩压室后蒸汽完全冷凝为水。在这个过程中,蒸汽的热量被冷水回收,同时冷凝水也被回收。图2(a)和图2(b)中引射器背压不同,蒸汽在引射器轴向存在的长度也不同,从喷嘴出口到蒸汽在引射器中消失的位置称为蒸汽羽翼长度,如图2中L所示。
羽翼长度受引射器边界条件的影响见图3。

图3 引射器中的蒸汽羽翼长度Fig 3 Wing length of steam-water in the ejector
从图3可以看出,在一、二次流压力、温度不变的情况下,蒸汽羽翼随背压的升高而变短。这表明随背压升高,引射器引射蒸汽的能力变弱,引射的蒸汽量变小因而蒸汽在较小的气液接触面积上就完全冷凝为水。
从图3还可以看出,增大一次流的压力,羽翼明显增长,这是由于水压升高,一次流动能相应增大,于是在引射器中能喷射更长。一次流水的温度升高降低了蒸汽和水的传热温差,降低了水对蒸汽的引射能力从而羽翼长度变短。二次流压力降低,引射器正常工作的背压大大降低,同时羽翼长度变短。
2.2 压力温度分布规律
沿引射器轴线的静压力p分布如图4所示。
从图4可以看出,压力在一次流喷嘴中急剧下降,到混合室入口下降到与二次流压力相近的水平,在混合室内压力基本保持不变,在喉部或混合室内经历一个跃升,然后在引射器喉部和扩压室继续缓慢升高直至引射器出口。背压的升高导致压力跃升的位置提前,对比蒸汽羽翼长度(图3)和压力跃升位置,可以发现压力跃升的位置和汽羽消失位置相同,表明蒸汽是在经历一个压力激波后完全冷凝。
图5为沿引射器轴线的温度分布。

图4 引射器中的压力变化Fig 4 Pressure variation in the ejector

图5 引射器中的温度变化Fig 5 Temperature variation in the ejector
从图5可以看出,在引射器的混合室和喉部,由于蒸汽的冷凝,水温不断升高,说明水吸收了蒸汽的显热量。在蒸汽冷凝完后,温度基本不变。由于随背压升高,引射蒸汽量减少,所以引射器出口水温随背压升高而降低。
2.3 引射系数和升温能力
图6为引射器引射系数ER受条件的影响。

图6 引射器引射系数Fig 6 Ejector coefficientof the ejector
从图6可以看出,随引射器出口背压的升高引射系数降低,表明背压升高导致引射器引射能力下降,与图3汽羽长度变短相对应,此时蒸汽冷凝所需传热面积减小。当一次流压力升高时,一次流流量也升高,同时引射的二次流流量也有所升高,二次流与一次流流量之比即引射系数可能增大也可能减小,本文一次流压力从140 kPa升至160 kPa时,引射系数只略有增加。当一次流水温升高时,由于蒸汽与水传热温差变小,所以冷凝的蒸汽量减少,引射系数相应减小。当二次流压力减小时,引射器正常工作的背压大大降低,同时引射系数降低。
稳定的结果表明羽翼长度长于引射器混合室长度(如图3),若图6中的背压继续增大,则数值计算无法给出稳定结果,不稳定的蒸汽羽翼在混合室内就消失,蒸汽在入口出现回流,蒸汽羽翼长度最终变为0。
引射器一次流进口冷水和出口水之间的温升如图7所示。
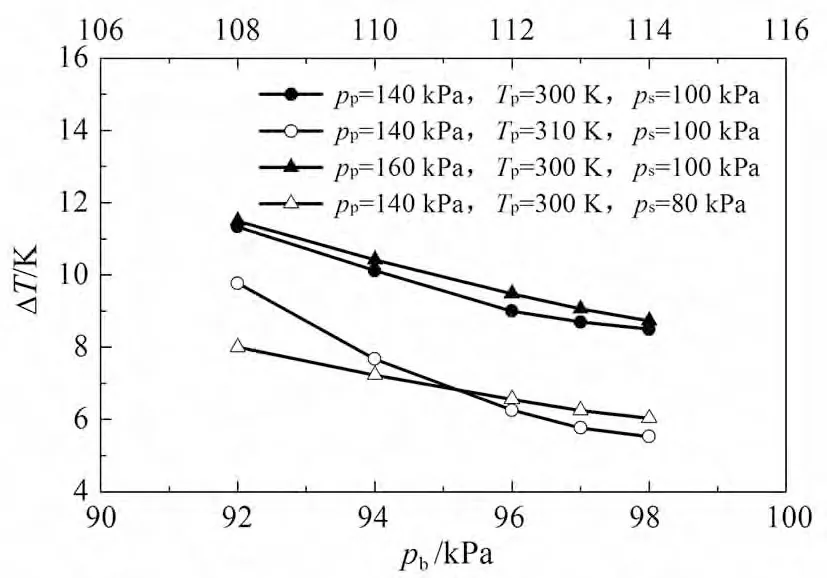
图7 引射器温升Fig 7 Temperature rising in the ejector
从图7可以看出,本文研究范围内引射器温升在5.33~11.49 K,表明水引射蒸汽引射器可以用来回收蒸汽热量。同时由于水的温度升高是由蒸汽冷凝引起,所以温升变化规律与图6中引射系数的变化规律相同。
严俊杰进行的水引射蒸汽引射器实验表明,引射系数和温升随背压升高而降低,随一次流参数升高而降低,随二次流参数升高而升高[14]。本文所得的引射系数和温升数值与实验还存在一定误差,故本文未加以对比,但考虑到所得规律与实验相同,表明本文使用的数值计算方法仍具有一定的参考价值。
3 结论
使用欧拉-欧拉两相流模型,结合热平衡冷凝模型对水引射蒸汽两相引射器进行了数值模拟,结果表明:
1)蒸汽羽翼长度随一次流压力的升高而升高,随一次流温度的升高和二次流压力的降低而降低,背压越大则羽翼越短;
2)混合室内压力基本保持不变,在喉部或扩压室内经历一个激波后压力迅速恢复,同时蒸汽在此处完全冷凝;
3)引射系数和温升随一次流压力升高而略有升高,随一次流温度升高和二次流压力降低而降低;引射器背压增大导致引射系数降低,背压增大到一定程度时,引射器出现回流。
[1]Xu R J,He Y L.A vapor injector-based novel regenerative organic Rankine cycle[J].Applied Thermal Engineering,2011,31(6/7):1238-1243.
[2]蔡琴,童明伟,沈斌,等.新型喷射式加热器的性能试验[J].排灌机械,2009,27(4):261-264.
[3]刘继平,严俊杰,陈国强,等.环周进汽两相流喷射升压过程实验研究[J].工程热物理学报,2004,25(sl):63-66.
[4]Varga S,Oliveira A C,Diaconu B.Numerical assessment of steam ejector efficiencies using CFD[J].International Journal of Refrigeration,2009,32(6):1203-1211.
[5]Sriveerakul T,Aphornratana S,Chunnanond K.Performance prediction ofsteam ejectorusing computational fluid dynamics:Part 1.Validation of the CFD results[J].International Journal of Thermal Sciences,2007,46(8):812-822.
[6]刘继平,严俊杰,邢秦安,等.自升压蒸汽动力循环的理论研究[J].西安交通大学学报,2003,37(9):885-888.
[7]童明伟,蔡琴,白秀娟.多喷嘴射水式喷射器加热性能分析[J].重庆大学学报,2011,34(6):60-62.
[8]马昕霞,袁益超,黄鸣,等.多喷嘴汽液两相喷射器的工作特性研究[J].中国电机工程学报,2012,32(14):56-64.
[9]Abe Y,Shibayama S.Study on the characteristics of the supersonic steam injector[J].Nuclear Engineering and Design,2014,268:191-202.
[10]蔡琴,童明伟,白秀娟,等.环周进汽型喷射器的火用效率分析[J].化工学报,2010,61(5):1078-1082.
[11]Zhang Z,Chong D,Yan J.Modeling and experimental investigation on water-driven steam injector for waste heat recovery[J].Applied Thermal Engineering,2012,40:189-197.
[12]Shah A,Chughtai I R,Inayat M H.Experimental and numerical analysis of steam jet pump[J].International Journal of Multiphase Flow,2011,37(10):1305-1314.
[13]Gulawani SS,Joshi JB,Shah M S,et al.CFD analysis of flow pattern and heat transfer in direct contact steam condensation[J].Chemical Engineering Science,2006,61(16):5204-5220.
[14]严俊杰,武心壮,种道彤,等.低温乏汽回收利用装置性能的实验研究[J].西安交通大学学报,2009,43(5):8-12.
[15]严俊杰,杨建军,张朋飞,等.低温乏汽回收利用装置的结构参数研究[J].西安交通大学学报,2010,44(1):1-4.
[16]Anglart H,Nylund O.CFD application to prediction of void distribution in two-phase bubbly flows in rod bundles[J].Nuclear Engineering and Design,1996,163:81-98.
[17]Hughmark G A.Mass and heat transfer from a rigid sphere[J].AIChE,1967,13(6):1219-1221.

