一个限制排中律适用范围的命题演算系统

曹 飞

（中共陕西省委党校哲学部，陕西西安710061）

在经典命题演算中，不矛盾律和排中律都普遍有效。直觉主义断然否定排中律的普遍有效性，在直觉主义命题演算中，不矛盾律普遍有效，排中律无效。直觉主义的创始人布劳维（L.E.J.B r o u w e r）认为：“排中律是从有限事物中概括出来的，任何一个涉及有限事物全体的命题，总是可以通过对这些事物逐一地加以验证，来判明该命题的真伪，这时排中律是有效的。但是如果忘记了排中律的有限来源，把排中律视为先于和高于数学的某种普遍适用的法则，并将它运用于无限的场合，就会犯错误。这是因为对于无限的事物，往往不可能（哪怕是原则上）对它们一一加以鉴别。”[1]49然而，经典命题演算认排中律为普遍有效式，这固然与直观相违；直觉主义命题演算认排中律为无效式，亦与直观不尽相符。从直观上看，正如布劳维所认为的那样，排中律对且只对有限事物有效；但无论是经典命题演算，还是直觉主义命题演算，都没有框定排中律的适用范围。鉴于此，本文拟对经典命题演算做适当改动，构造一个限制排中律适用范围的命题演算系统P C5。

一、命题演算系统PC5及其可靠性、完全性

（一）PC5的语法和语义

1．语法。

初始符号：甲、p1，p2，p3，…，pm，…，m 为自然数；乙、┌ ，┐，∨；丙、（，）。

在陈述形成规则以前，我们先引进一些语法语言的符号并作如下说明：

（1）Q、R、S代表任一甲类符号。

（2）X、Y、Z代表任一符号序列。

（3）A、B、C、D、E 代表任一合式公式。

（4）语法符号“┠”写在任一公式之前，它表示紧接在后面的公式是本系统所要肯定的。

形成规则：

（1）若X是甲类符号，则┌X、┐X是合式公式。

（2）若X是合式公式，则┌X、┐X是合式公式。

（3）若X和Y都是合式公式，则（X∨Y）是合式公式。

（4）只有适合以上三条的符号序列是合式公式。

定义：

（甲）（A→B）定义为（┐A∨B）。

（乙）（A∧B）定义为┐（┐A∨┐B）。

（丙）（A≡B）定义为（（A→B）∧（B→A））。

括号省略规则：

（甲）最外面的一对括号可以省略。

（乙）真值联结词的结合力依下列次序而递增：≡，→，∧，∨，┌，┐。公理：

公理 1：┠A∨A→A；

公理 2：┠A→A∨B；

公理 3：┠A∨B→B∨A；

公理 4：┠（B→C）→（A∨B→A∨C）；

公理5：┠┌A≡A；

公理6：┠ ┐（┌Q∧┐Q）。

变形规则：

（1）分离规则，从┠A和┠ ┐A∨B可得┠B。

（2）定义置换规则，定义的左右两方可相互替换。设原公式为A，替换后所得公式为B，则从┠A可得┠B。

公式的级的递归定义：

（1）若X是甲类符号，则┌X和┐X均为原子公式，原子公式是1级公式。

（2）若X是m级公式，则┌ X和┐X均为m+1级公式。

（3）若 X 是 m 级公式，Y 是 n级公式，且 m≥n，则 X∨Y、Y∨X、X∧Y、Y∧X、X→Y、Y→X、X≡Y、Y≡X均为m级公式。

2.语义。

（1）甲类符号是0级命题变项，代表任意的0级命题。

（2）乙类符号是联结词符号，其中┌代表肯定词“是”，┐代表否定词“不”，∨代表析取词“或者”，它们的真值表如下（其中T表示“真”，F表示“假”，U表示“非真非假”）：

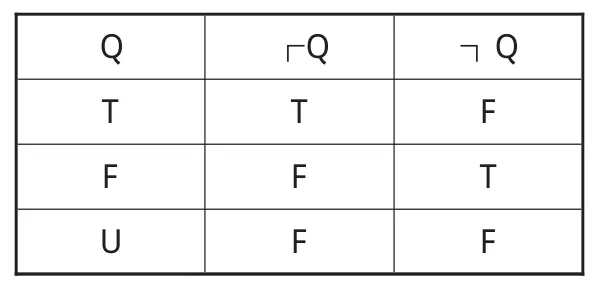
（表1）

（表2）

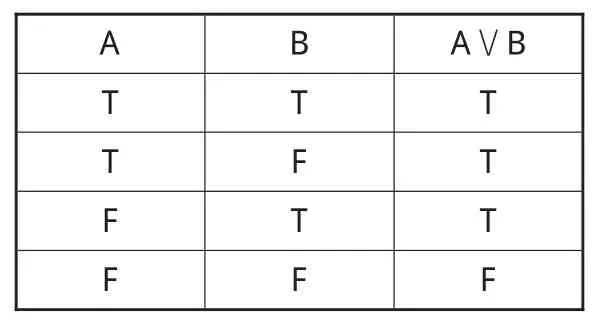
（表3）

（3）丙类符号为左右括号。

下面我们引入重言式的定义：A为重言式，当且仅当不管A中的0级命题变项取何值，A的值均为T。

3．定理的证明。

我们可以将PC5中相同的原子公式看作经典命题演算中相同的命题变项，将PC5的不同的原子公式看作经典命题演算中不同的命题变项，这样我们就可以将PC5看作经典命题演算的扩充[2]37～39。因此，经典命题演算的定理都是PC5的定理。PC5的其他定理的证明，这里仅举4例。

基本置换定理 令DA表示A是D的组成部分，设已证├A→B和├B→A，并且以公式B置换DA中的公式 A 得 DB，则可得├DA→DB和├DB→DA。因之，从├DA，可得├DB。本规则称为“置换”。简单地说，如果A和B等值，则从├DA可得├DB。

基本置换定理的证明。基本置换定理的严格证明要应用数学归纳法，要施归纳于合式公式的构造。本文采取了较为简单的、不完全严格的证明。

兹证明此定理在以下最简单的情况下是正确的：（1）A在DA中只出现一次；（2）DA的形式是：（甲）┌A，（乙）┐A，（丙）C∨A，或（丁）A∨C。根据形成规则，不论DA的形式如何复杂，总是由多次重复地运用肯定、否定、析取构成的，所以，一般的情况只是以上情况的简单重复。

在这里虽然没有明确地提出数学归纳法，只提出“一般的情况是简单情况的重复”，但是，证明的基本思想以及证明的保证还是数学归纳法。

有了上述定理，我们就可以证明PC5的完全性。

（二）PC5的可靠性

PC5的可靠性定理：PC5的定理都是重言式。

证明的思路是：第一，PC5的公理都是重言式；第二，应用PC5变形规则，从重言式只能得到重言式。因之可得结论：PC5的定理都是重言式。证明从略。

（三）PC5的完全性

为了证明PC5的完全性，我们不妨先引进合取范式这一概念。

1.合取范式。

定义1.1A是简单析取式是指它是形如Al∨A2∨…∨An（n∈N且n≥1）的公式，其中每个Ai（1≤i≤n）皆为原子公式或原子公式的否定，称Ai为简单析取式的成员。

定义1.2A是合取范式是指它是形如Al∧A2∧…∧An（n∈N且n≥1）的公式，其中每个Ai（1≤i≤n）皆为简单析取式，称Ai为合取范式的成员。

定义1.3 A是一公式，A′是A的合取范式是指A′满足：A与A′等值，即A≡A′是重言式，并且A′是合取范式。

一个公式的合取范式是否一定存在?如何求一个公式的合取范式?

根据定义，合取范式在表达方面的特征有：（1）没有→和≡符号；（2）肯定符┌只出现于0级命题变项之前；（3）否定符┐只出现于0级命题变项或原子公式之前；（4）是一个简单析取式的合取或单独的一个简单析取式。

因之，求一个公式的合取范式，包括这样几个具体步骤：

第一，把公式中可能包含的→和≡完全销去。即用（┐A∨B）置换A→B，用（A∧B）∨（┐A∧┐B）或（┐A∨B）∧（A∨┐B）置换 A≡B。

第二，销去多余的肯定符┌。即用A置换┌A。

第三，将┐逐步内移至原子公式之前，并销去多余的否定符┐。即用┐A∧┐B置换┐（A∨B），用┐A∨┐B置换┐（A∧B），用A置换┐┐A。

经过上述三个步骤后，公式中只包含原子公式及其否定，以及∨和∧。

第四，在上述步骤的基础上，用（A∨B）∧（A∨C）置换A∨（B∧C）就得到原公式的合取范式。

以上这些置换规则都有系统内的根据。或是一个定义，例如→的销去；或是定理，例如多余的肯定符┌和多余的否定符┐的销去。置换的结果与原公式是等值的。

任何公式，运用上述方法，都能在有限步内求得其合取范式。因此，任一公式都有其合取范式。

2.PC5的完全性定理：重言式都是PC5的定理。

证明：设A为一重言式。A有一合取范式。设A的合取范式为B，B也是重言式，并且B为B1∧B2∧…∧Bn，Bi（1≤i≤n）为简单析取式，Bi必是重言式。每一Bi里必有一0级命题变项Q，并且至少满足下列条件之一：（甲）┐┌Q和┐┐Q都作为Bi的析取支出现；（乙）┌Q和┐┌Q都作为Bi的析取支出现；（丙）┐Q和┐┐Q都作为Bi的析取支出现。因为：若有一Bi里每一个0级命题变项Q，都不满足（甲）（乙）（丙）三个条件中的任何一个条件，则该Bi里任何一个0级命题变项Q，必处于下述三种情形之一：（1）┌Q和┐┐Q都作为Bi的析取支出现，或其中之一作为Bi的析取支出现；（2）┐Q和┐┌Q都作为Bi的析取支出现，或其中之一作为Bi的析取支出现；（3）┌Q和┐Q都作为Bi的析取支出现。对于该Bi里任一0级命题变项Q，若它处于第一种情形则取值F，若它处于第二种情形则取值T，若它处于第三种情形则取值U，此时该Bi的每一个析取支的值均为F，该Bi的值为F。该Bi不是重言式。这与Bi必是重言式相矛盾。所以，每一Bi里必有一0级命题变项Q，并且至少满足（甲）（乙）（丙）三条件之一，即每一Bi必具有形式┐┌Q∨┐┐Q或┐┌Q∨┐┐Q∨C或⊿∨┐⊿或⊿∨┐⊿∨C（其中⊿代表任一原子公式）。因┐┌Q∨┐┐Q、┐┌Q∨┐┐Q∨C、A∨┐A、A∨┐A∨C均可证，所以，每一Bi都可证。根据定理┠A→（B→A∧B），B1∧B2∧…∧Bn可证。所以，B可证。B是A的范式，是从A根据置换规则得到的，如B可证，则A也可证。可见如A是重言式，则A可证。凡重言式皆可证，故PC5是完全的。

二、PC5的一个重要特征：不矛盾律普遍有效，排中律在且只在一定范围内有效

在PC5中有定理┠ ┐（┌A∧┐A）和┠ ┐（┌Q∧┐Q）。这说明，在PC5中对于任意的n（n∈N且n≥0）级命题而言，都不能同时既肯定又否定它，不矛盾律都成立。

在PC5中虽有定理┠┌A∨┐A，但┌Q∨┐Q不是PC5的定理。这说明，在PC5中对于任意的n（n∈N且n≥1）级命题而言，或者肯定它，或者否定它，二者必居其一，排中律成立；但对于任意的0级命题而言，可以既不肯定它，也不否定它，排中律不成立。

在PC5中有定理┠ ┐（┌┌A∧┌ ┐A）和┠ ┐（┐┌A∧ ┐┐A）。这说明，在PC5中不能同时肯定┌A和┐A，也不能同时否定┌A和┐A。从真值表看，┌A和┐A不能同真，也不能同假。可见，在PC5中，肯定和否定同一个n（n∈N且n≥1）级命题而形成的两个相反命题，是矛盾关系。这说明，对于任意的肯定和否定同一个n（n∈N且n≥1）级命题而形成的两个相反命题而言，不矛盾律和排中律均成立。

在PC5中有定理┠ ┐（┌┌Q∧┌ ┐Q）。这说明，在PC5中不能同时肯定┌Q和┐Q。┐（┐┌Q∧┐┐Q）不是PC5的定理。这说明，在PC5中可以同时否定┌Q和┐Q。从真值表看，┌Q和┐Q不能同真，但可以同假。可见，在PC5中，肯定和否定同一个0级命题而形成的两个相反命题，并不是矛盾关系，而是反对关系。这说明，对于任意的肯定和否定同一个0级命题而形成的两个相反命题而言，不矛盾律成立，但排中律不成立。

总之，对于任意的肯定和否定同一个n（n∈N且n≥0）级命题而形成的两个相反命题而言，不矛盾律都成立；对于任意的肯定和否定同一个n（n∈N且n≥1）级命题而形成的两个相反命题而言，排中律成立，但对于任意的肯定和否定同一个0级命题而形成的两个相反命题而言，排中律不成立。

这里需要说明的是：从直观上看，0级命题陈述的是对象情况，而对象可能是无限的事物，因而对于任意的肯定和否定同一个0级命题而形成的两个相反命题而言，排中律不成立；n（n∈N且n≥1）级命题陈述的是思想情况（例如：否定一个命题而形成的命题陈述的就是一命题之否定这一思想情况），而思想总是有限的（即使是无限的对象也只能用有限的思想来把握），因而对于任意的肯定和否定同一个n（n∈N且n≥1）级命题而形成的两个相反命题而言，排中律成立。由此可见，PC5对排中律的适用范围的限定是完全符合人们的直观的。

三、反证法的适用范围问题

下面我们以PC5为逻辑基础，简要地讨论反证法的适用范围问题。

在PC5中有下列定理：

┠┌A≡┐┐A

这一定理表明，一个n（n∈N且n≥1）级命题的肯定命题和它的否定之否定命题可以互推，反证法适用于论证n（n∈N且n≥1）级命题的肯定命题。

┠┐A≡┐┌A

这一定理表明，一个n（n∈N且n≥1）级命题的否定命题和它的肯定之否定命题可以互推，反证法适用于论证n（n∈N且n≥1）级命题的否定命题。

在PC5中有下列定理：

┠┌Q→┐┐Q

这一定理表明，从一个0级命题的肯定命题可推出该0级命题的否定之否定命题。

┐┐Q→┌Q不是PC5的定理。这说明，从一个0级命题的否定之否定命题不能推出该0级命题的肯定命题，也就是说，反证法不适用于论证0级命题的肯定命题。

┠┐Q→┐┌Q

这一定理表明，从一个0级命题的否定命题可推出该0级命题的肯定之否定命题。

┐┌Q→┐Q不是PC5的定理。这说明，从一个0级命题的肯定之否定命题不能推出该0级命题的否定命题，也就是说，反证法不适用于论证0级命题的否定命题。

综上所述，反证法适用于论证n（n∈N且n≥1）级命题的肯定或否定命题，但不适用于论证0级命题的肯定或否定命题。

四、对引入0级命题变项和肯定词符号的一点说明

如前文所述，0级命题变项代表任意的0级命题。0级命题就是不包含肯定词或否定词的命题。

这里有一点需要说明，逻辑学界有一种普遍流行的观点，这种观点认为任何命题都肯定了自身。按照这种观点，人们必须承认：第一，任何命题都隐含着肯定词；第二，一个命题与肯定该命题而形成的命题是等值的。这样一来，也就不存在0级命题了。

笔者认为，上述普遍流行的观点颇值得商榷。首先，没有任何理由可以证明任何命题都肯定了自身。其次，有些命题很难说肯定了自身。例如，命题甲“圆周率π的小数表达式3．1415926…中有七个连续出现的5”就很难说肯定了自身。π是一个无理数，即无限的不循环的小数。到目前为止，我们还没有发现（或证明）π的小数展开式中有七个连续出现的5，因而不能肯定命题甲；我们也无法论证π一定没有这样一个特性，因而也不能否定命题甲[1]49～50。如果命题甲肯定了自身，那么只要提出命题甲，就提出了对命题甲的肯定。这与命题甲虽已提出来但到目前为止还未被肯定这一事实显然不符。再次，“一个命题与肯定该命题而形成的命题是等值的”只是逻辑学的一个公设，基于这一公设，肯定词在任何情况下都可以随意消除，人们在构造命题演算系统时根本无需引入肯定词，这就造成了在现代逻辑中对肯定词和否定词的研究极为不平衡的奇特现象：人们建立了多种多样的命题演算系统来刻画否定词的逻辑意义，区分了不同种类的否定（如经典否定、直觉主义否定、弗协调否定等）[3]476～477；但人们对肯定词的逻辑意义却极少关注。然而，值得提出的是，上述公设从未得到过系统外的预先证明。鉴于此，本文所建构的形式系统在限制上述公设适用范围的基础上引入了0级命题变项和肯定词符号。

[1]冯棉．经典逻辑与直觉主义逻辑[M]．上海：上海人民出版社，1989．

[2]王宪钧．数理逻辑引论[M]．北京：北京大学出版社，1982．

[3]罗·格勃尔．哲学逻辑[M]．张清宇，陈慕泽，等，译．北京：中国人民大学出版社，2008．