一类混合隔振系统非线性动力特性分析

宋秉明，吕志强，帅长庚

（1.海军工程大学　振动与噪声研究所，武汉430033；2.海军工程大学　船舶振动噪声重点实验室，武汉430033）

一类混合隔振系统非线性动力特性分析

宋秉明1，2，吕志强1，2，帅长庚1，2

（1.海军工程大学振动与噪声研究所，武汉430033；2.海军工程大学船舶振动噪声重点实验室，武汉430033）

研究磁悬浮—气囊主被动混合隔振系统的非线性动力特性，包括对系统的稳定性分析和位移响应的计算及其模拟仿真。通过对磁悬浮—气囊主被动混合隔振装置的简化，建立与之相适应的非线性动力微分方程；利用谐波平衡法对非线性微分方程进行求解，研究系统方程的幅频响应曲线在不同参数下的变化规律；由Lyapunov稳定性定理对系统进行稳定性判断；通过Simulink软件对整个系统进行模拟仿真得出位移的功率谱曲线，分析结果表明混合隔振系统在低频激励下的稳定性更好，隔振效果明显。

振动与波；混合隔振；非线性动力特性；磁悬浮作动器；空气弹簧

随着隔振技术的不断创新和改善，磁悬浮隔振装置越来越受到国内外学者和专家的青睐，对此的研究和分析也很多［1-4］。磁悬浮作动器具有固有的非线性特性，对磁悬浮—气囊主被动混合隔振器的研究是将非线性微分方程化为线性或者近似线性来求解振动响应，而忽略了位移非线性项［5］，导致计算所得的位移响应值精度有限，这也影响后续的分析结果。对于磁悬浮作动器，即便是微小的位移变化，所带来的影响也不容忽视，对于隔振系统非线性现象的研究内容和方法很多［6-8］。本文采用谐波平衡法，对磁悬浮—气囊主被动混合隔振系统在不同参数下的非线性动力特性进行研究，对位移非线性给系统带来的影响进行深入分析。

1　建立运动微分方程

磁悬浮—气囊主被动混合隔振器是将无接触的、等效刚度低的磁悬浮作动器集成到气囊隔振器内部，利用气囊隔离宽频振动，同时控制作动器消除低频线谱振动的主、被动一体化的混合隔振装置［9］。基本结构简图如图1所示，主要由气囊、永磁铁、铁芯、线圈和衔铁等构成。

图1　磁悬浮—气囊混合隔振系统实体简图

对混合隔振系统进行数学建模，将气囊简化为一个包含线性刚度和线性阻尼的被动隔振部件，主动控制部分简化为磁铁的交变磁悬浮力，得到如图2所示的力学模型。其中m是隔振对象的质量；k1和c1分别是气囊的等效刚度和阻尼；x是隔振对象的位移；fd是外部激励力；Fg是作动器提供的主动交变磁悬浮力，同时作用在隔振对象和基础上。此处假设基础为刚性的。

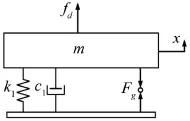
图2　磁悬浮—气囊混合隔振系统力学模型

由以上力学模型，结合振动理论分析可知混合隔振系统的运动微分方程为

mx¨（t）+c1x˙（t）+k1x（t）=fd（t）-Fg（t）（1）式中，Fg（t）为交变磁悬浮力，参考何琳［9］和谢强［5］研究分析时采用的交变电磁力模型，可得交变磁悬浮力的表达式为

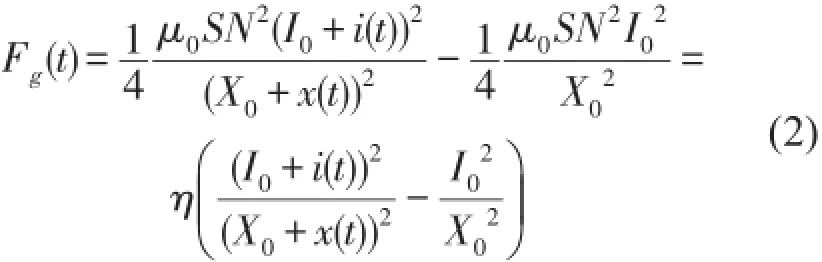
在平衡点（I0，X0）处对Fg（t）进行泰勒级数展开，整理得式中，第一个括号内的表达式为磁悬浮作动器的可控输出力，记作fa（t）。其中电流平方项i2对系统的影响在文献中已有研究分析，并采用补偿控制对其进行消除［5］。同时，本文主要分析研究位移非线性对系统的影响，故此处忽略电流平方项；又由计算可知电流立方项i3的系数为零，则

第二个括号内的表达式为磁悬浮作动器的等效位移刚度，记作ka。此处只考虑偏置电流I0对等效刚度ka的影响，忽略交变电流i的影响，则

G（x）为系统的位移非线性项，由于振动过程中位移为小量，为简化计算量，略去三阶以上的高阶项，此处只考虑平方、立方项，则

将式（4）、（5）、（6）代入式（1），两边同时除以质量m得最终简化的微分方程

其中

磁悬浮主被动混合隔振系统采用的是有源振动控制，在控制系统中引入次级振源，通过测量主振源的振动信号，再采用适当的控制算法，使得次级振源与主振源的大小相等，方向相反，从而达到隔振的目的。由此，易知对于单频激励力fd（t），要达到隔振的目的，主动控制力fa（t）的频率必然与激励力fd（t）的频率相同。为了便于后续的分析，对f（t）作进一步简化得式中，F为激励力与主动控制力之差的幅值，ω为激励频率。

2　系统的稳定性分析

设x（t）=x1，则由（7）式可知系统的非线性状态方程如下

写成矩阵形式为

设X=Ax+B，求解矩阵A的特征值，则有

解得

由Lyapunov稳定性定理［10］可知，当λ1、λ2为一对实部为负的共轭复根时，奇点即为焦点，系统具有渐进稳定性。由此可知，磁悬浮混合隔振系统具有良好的稳定性。

3　方程求解

采用谐波平衡法［10］对非线性微分方程（7）求解，设x（t）为周期解，用Fourier级数展开，得到如下通解形式

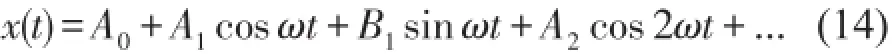
此处A0=0，忽略高次谐波项，设非线性方程（7）的近似解为

由式（11）易得x˙（t）、x¨（t）的表达式，又可知

将x（t）、x˙（t）、x¨（t）、x2（t）及x3（t）的表达式代入（7）式中，整理得

设

求解式（17）中的方程组，从而求得Z和φ，即可得方程的近似解。

4　数值计算与仿真分析

利用Matlab中的ezplot函数对方程（16）进行绘图，可得主被动混合隔振系统的幅频响应随不同参数变化的规律曲线。为了便于观察其变化规律，此处将模型参数设为m=1 kg，ωn=1rad/s，分析结果如图3、图4、图5所示，分别表示不同β、μ、F值下的幅频响应曲线，纵坐标表示幅值，横坐标频率比表示的是激励频率与固有频率的比值

图3　不同β值下的幅频响应曲线（其中μ=0.1，F=0.5）

由图3可知，当β＞0时，随着非线性项系数β的增大，幅值的峰值随之减小，并且向右侧偏移的倾角变大。由图4易知，随着阻尼项系数μ的增大，幅值的峰值随之减小，但对幅值的偏向程度没有影响，并且当达到一定值时，跳跃现象消失，使得隔振区间增大、隔振效果加强。由图5可知，幅值随着F的增大而增大，并且有效隔振区间随之减小，但对于整个频段的收敛效果也变差，使得隔振效果不理想。

根据系统的运动微分方程（7），运用Matlab/ Simulink软件对磁悬浮—气囊隔振系统模型进行仿真分析，仿真计算过程主要是利用软件内部的ode 45算法对系统的运动微分方程进行数值求解。对于被动隔振的仿真分析，则将主动控制力中的交变电流值设为零。

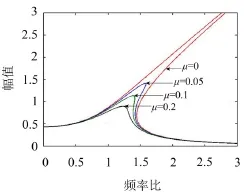
图4　不同μ值下的幅频响应曲线（其中F=0.5，β=1）

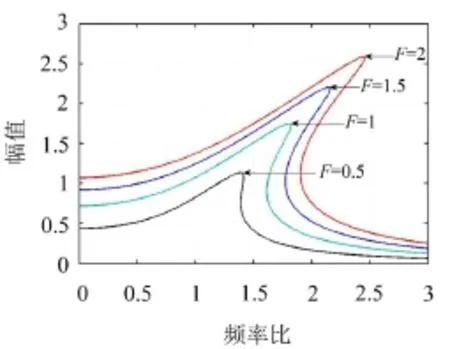
图5　不同F值下的幅频响应曲线（其中μ=0.1，β=1）

通过改变仿真模型中激励频率ω的值（10 π～100 π），使模型分别在被动隔振和主动隔振的状态下进行仿真分析。对于位移的幅值，按照的方法转换为dB的形式观察功率谱变化规律，其中参考值Zs=1 pm。图6所示的是在激励频率为40 π时的单边功率谱曲线，系统由静止状态被激励，时间T持续10 s。

由被动隔振的功率谱曲线可知，系统在前5 s的幅值峰值点有两个，分别为系统固有频率处和激励频率处，而后5 s的曲线中固有频率处的峰值则削弱了，这主要是由于位移响应解中的瞬态解引起的，在阻尼c1大于0的情况下，当时间足够大时可以将这部分解忽略不计，只考虑稳态解；对于主动隔振系统，由图6可知不存在这一情况，充分表明主动控制对系统固有频率处振动控制的实时性和有效性。比较5 s～10 s的被动隔振与主动隔振的功率谱曲线可知，在激励频率20 Hz处，主动隔振比被动隔振小37.5 dB，表明主动隔振的效果明显。但是在40 Hz、60 Hz等激励频率的倍频处产生多个峰值，产生额外的能量，这主要是由于主动控制中位移非线性项所导致的。

表1所示的是激励频率ω在10 π～100 π区间内隔振系统在激励频率处的功率谱峰值的仿真数据表。

图6　不同隔振状态下的功率谱曲线

表1　不同激励频率下被动隔振和主动隔振在激励频率处功率谱的峰值

由表中数据可知，被动隔振系统在激励频率处的隔振效果随着激励频率的增大越来越好，这也证实了气囊隔振对高频激励有良好的隔振性能；主动隔振系统在激励频率处的隔振效果随激励频率变化不大，维持在133 dB左右，这表现出主动隔振的稳定性和可靠性，但相比被动隔振有良好的隔振效果，通过将主动隔振的值减去被动隔振的值可以得到证实。此外，主动控制在高频处的隔振效果在逐渐减小。

5　结语

基于气囊—磁悬浮主被动混合隔振系统，对其非线性动力特性进行研究分析，结论如下：

（1）运用Lyapunov稳定性定理对混合隔振系统的稳定性进行判断，并结合仿真分析的结果可知磁悬浮混合隔振系统具有良好的稳定性；

（2）运用谐波平衡法对建立的运动微分方程进行解析，得到不同参数下非线性微分方程的频响曲线及其变化规律；

（3）运用Simulink软件对系统模型进行仿真分析，得到不同时间范围不同隔振状态下系统的功率谱图，可知主动隔振在低频处的隔振效果明显优于被动隔振，但位移非线性项的影响会使得主动隔振在倍频处产生附加能量。

［1］何琳，徐伟.舰船隔振装置技术及其进展［J］.声学学报，2013，389（2）：128-136.

［2］徐洋，华宏星，张志谊，等.舰船主动隔振技术综述［J］.舰船科学技术，2008，30（2）：27-33.

［3］PKTripathi，KVGangadharan.Coilbased electromagnetic semi-active vibration control for flexible structures［J］.AnnalsofFacultyEngineering Hunedoara-InternationalJournalofEngineering，2012:185-190.

［4］R.A.Ibrahim.Recent advances in nonlinear passive vibration isolators［J］.Journal of Sound and Vibration，2008，（314）:371-452.

［5］谢强，帅长庚，李彦.主动控制中作动器非线性谐频的控制［J］.噪声与振动控制，2013，33（1）：56-58.

［6］胡光军.一种非线性隔振器的设计及实验研究［D］.上海：上海交通大学，2011.

［7］Shu-Yong Liu，Xiang Yu，Shi-Jian Zhu.Study on the chaos anti-control technology in vibration isolation system［J］. Journal of Sound and Vibration，2008，（310）:855-864.

［8］Jiaorui Li，Wei Xu，Xiaoli Yang.Chaotic motion of van der pol-mathieu-duffing system under bounded noise parametricexcitation［J］.JournalofSoundand Vibration，2008，（309）:330-337.

［9］何琳，李彦，杨军.磁悬浮—气囊主被动混合隔振装置理论和实验［J］.声学学报，2013，38（2）：241-249.

［10］胡海岩.应用非线性动力学［M］.北京：航空工业出版社，2000.

Nonlinear Dynamic CharacteristicsAnalysis of a Passive-active Hybrid Vibration Isolation System

SONG Bing-ming1，2，LV Zhi-qiang1，2，SHUAI Chang-geng1，2
（1.Institute of Noise and Vibration，Naval University of Engineering，Wuhan 430033，China；2.National Key Laboratory on Ship Vibration&Noise，Naval University of Engineering，Wuhan 430033，China）

The nonlinear dynamic characteristics of a passive-active hybrid vibration isolator system using electromagnetic actuator and air spring were studied.The study contained stability analysis，computation and simulation of displacement responses.The nonlinear dynamic differential equation was established by simplifying the passive-active hybrid vibration isolation.The solution of nonlinear differential equation was obtained by using harmonic balance method. The amplitude-frequency response curves of the system equation with different parameters were studied.Stability of the system was judged by Lyapunov stability theorem.The power spectrum curves of displacement were obtained by simulation of the system with Simulink.It is shown that the stability and the vibration isolation efficiency of the system with active control is good.

vibration and wave；hybrid vibration isolation；nonlinear dynamic characteristics；electromagnetic actuator；air spring

O322文献识别码：ADOI编码：10.3969/j.issn.1006-1335.2015.05.037

1006-1355（2015）05-0176-04+184

2015－03－09

宋秉明（1992－），男，江西省奉新人，硕士生，主要研究方向：振动与噪声控制。

吕志强，男，硕士生导师。

E-mail:whhg_sl@126.com