基于改进BP神经网络的轧机扭振智能控制

时培明　，李冰洋

（燕山大学　电气工程学院，河北　秦皇岛066004）

基于改进BP神经网络的轧机扭振智能控制

时培明，李冰洋

（燕山大学电气工程学院，河北秦皇岛066004）

针对轧机传动系统扭振控制问题，建立考虑负载转矩的轧机传动系统动力学模型。考虑到扭振模型比较复杂和参数不易测量的特点，提出基于神经网络的状态观测器，并对标准BP网络进行优化处理。设计基于改进BP神经网络状态观测器的智能控制系统，并利用SIMULINK对轧机实例进行仿真。结果表明设计的智能控制系统对轧机传动系统的扭振有良好的控制效果。

振动与波；轧机传动系统；扭振；改进BP神经网络；状态观测器

随着轧机装备水平的提高，相应对传动系统提出了高精度和高动态性能的技术要求。为了适应现代轧钢工业的发展，我国轧机在近期都进行了大规模电气自动化系统的技术更新改造，轧机传动已由先进的交流调速取代传统的直流调速，大大提高了轧机传动的技术性能指标。但轧机大多利用原机械设备，机械与电气配合不好，容易出现传动系统的扭振现象，扭振作为轧机传动系统的一个外部扰动环节，会引起系统动态速降，甚至破坏控制系统的稳定性，另一方面对轧机的破坏非常严重。扭振使传动部件产生疲劳损伤，降低部件的使用寿命。剧烈的振动还会引起部件的突然破坏性断裂，造成很大的经济损失［1］。

针对大型连轧机传动系统频繁出现轧机传动振动事故，国内外学者进行了大量的研究，以解决轧机扭振对轧钢生产的影响［2］。但这些研究成果基本上是从轧机传动机械与工艺条件出发，通过对机械系统的合理设计或者改变系统的参数，如电机和轧辊的转动惯量，弹性轴的刚度等来减小机电共振现象，很少涉及轧制扰动对电气系统的影响，以及从电气传动自动化系统的角度来解决轧机传动机电振动的问题。

随着现代控制理论的发展，尤其是智能控制的出现，为扭振的抑制提供了新的思路。本文针对轧机模型比较复杂和参数不易测量的特点，提出基于神经网络的状态观测器，并对标准BP网络进行优化处理。在理论分析的基础上，进一步通过仿真研究对这种方法的可行性和有效性进行验证。

1　轧机传动系统的扭振模型

构成一台轧机传动系统的机械传动部件很多，可以认为轧机的主传动系统是一个由若干惯性部件和弹性部件构成的“质量弹簧系统”。为了便于计算组合，传动系统可以对惯性部件与弹性部件进行合并，使整个系统得以简化，忽略连接轴阻尼，将其看成是由电动机和轧辊通过连接轴连接在一起的二质量系统，如图1所示。

图1轧机二质量系统模型

图1中Me是电机输出电磁转矩；Mω是轧机轧制转矩；ML是负荷转矩；ωm是电机旋转角频率；ωL是轧机旋转角频率；Jm是电机转动惯量；JL是轧机转动惯量；θm是电机旋转角度；θL是轧机旋转角度；K是连接轴弹性系数。

根据运动学方程式写出微分方程式得

对（2）两边微分可得

由（1）（2）和（3）可以写出电机模型的状态方程：

把状态方程式进行拉式变换得

由（5）得轧机二质量系统结构框图，如图2所示。

图2　二质量系统结构框图

2　改进BP神经网络状态观测器

2.1改进BP神经网络

标准BP网络模型把应用转换为了一个数学优化问题，把训练样本的输入输出问题转变成了一个非线性数学优化方面的问题。BP神经网络根据Widrow-Hoff规则，在学习算法方面使用数学优化算法中的最速下降算法，BP学习算法是一个全局逼近的优化算法。因而，具有一个很好的泛化能力和较强的容错性。从理论方面来说，BP网络具有非常强的非线性映射能力，只要BP神经网络的隐含层层数和隐含层的神经元节点数足够多，那么网络就可以完成对任意非线性映射的逼近。但是，它也有着许多缺点：收敛速度慢，在学习过程中，学习速率的收敛情况比较慢。因此，BP算法容易出现一个吋间比较长的输出误差“平原”，即出现数学上所说的平台；易陷入局部最小，无法确保算法是否收敛到了全局最小点。既然，标准BP网络算法是一个数值优化方面的非线性优化问题，那么，局部极小值的问题就不可避免地存在。BP网络是沿着一个局部的方向来逐渐改善网络的极值，然后希望使输出误差函数达到最小化的一组全局解，但是，实际上得到的往往是一个局部极小值。因此，需要对标准的BP算法进行改进［4］。

标准BP网络采用的优化算法是梯度下降法，但是因为该方法搜索的效率比较低，并且其学习率是固定的，这就不可避免的会产生某些缺陷。本文针对标准BP网络学习速率是固定这一缺点，提出一个全新的改进方案。在BP网络中，误差反向传播的时候，神经元节点间的连接权系数不同，那么将采用不同的学习速率，然后对其进行寻优搜索。对于输出层与隐层间的那些连接权系数wip1，wip2，…wipm，在反向传播调节的时候，将采用不同的学习速率，釆用不同的学习率η1，η2，…，ηm对其进行调整。对于不同神经元节点间的那些差异性的调节，都可以使学习率的自适应能力得到最大限度地调动，而且也可以尽最大努力在学习中满足权系数的多变要求。在对传统的学习率自适应方法改进后，该方法的误差反向传播过程如图3所示。

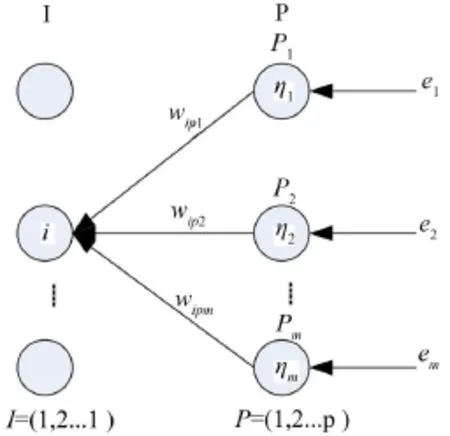
图3　改进后误差反向调节过程

经过改进的新学习速率算法，可以随机选取算法中学习步长η的起始值。但是新算法的学习步长是不固定的，在寻求目标函数E（）w的最小值过程中，会对算法的学习步长进行调整，调整公式可为

公式（6）中，m是实数范围内的一个常数，取值为2或3；λ的值是由一个符号函数确定的，值为-1或1，由决定的。

新算法学习步长的调整步骤如下：

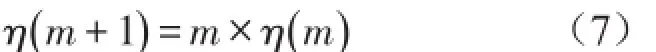
综上，新算法的连接权系数调节公式如式（9）所示

2.2神经网络状态观测器的实现方法

从采用的轧机传动二质量系统结构中，取连接轴扭矩MSH及轧辊转速ωL分别做前馈控制和反馈控制，组成复合控制系统。但是，实际生产中对这两个量的直接测量是非常困难的，因此利用本文设计的改进BP神经网络状态观测器对其进行观测。

神经网络状态观测器的结构如图4所示，把待观测的原轧机系统的输入u和输出y作为观测器的输入，而观测器的输出x^就是需要观测的原系统的状态［6］。这个原轧机系统就是图2所示的轧机二质量系统。设计神经网络状态观测器的核心问题是设计一个神经网络来逼近原系统状态变量与输入变量的关系映射，当逼近成功也就是学习完成时，神经网络的输出就是原系统的状态［7］，并且观测器只用到了原系统的输出函数，这也从原理上说明神经网络状态观测器对系统模型没有依赖。在使用神经网络状态观测器之前，神经网络状态观测器需要用到输出估计值与实际值的偏差，并用它来训练神经网络，进行权值的调整［8，9］。观测器中的网络类型就是上文中介绍的改进BP神经网络。

图4　神经网络状态观测器结构图

据图4神经网络状态观测器的结构可以得到用于轧机传动系统的神经网络状态观测器，如图5所示。观测器的输入为轧机传动系统的输入变量电机的输出转矩Me、负载转矩ML和系统的输出变量电机转速ωM，这三个量都是可直接测量的量。观测器的输出为需要观测的两个系统变量轧辊转速ωL和连接轴扭矩MSH。神经网络是一个5 入3出的BP网络，输入层有5个结点，分别用来接收3个状态变量的估计值以及两个系统输入变量，神经网络的输出层有3个结点，分别用来输出3个系统状态变量估计值，其中轧辊转速的观测值经过含有反馈放大系数Km环节后输出到加法器与设定值进行比较；连接轴扭矩观测值经过前馈补偿控制器Ga（S）作用，然后加到速度调节器的输出上。

图5　轧机传动系统的神经网络状态观测器

3　仿真实验及结果

首先利用传统的双闭环控制系统产生的数据对神经网络进行离线训练，此模型采用三层BP网络，网络的初始值设置为［0，0.5］之间的随机数，网络的输入层、隐层和输出层的节点数分别为5、10、3。具体算法如下：

性能指标误差函数为

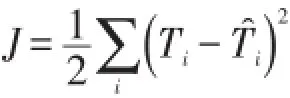
神经元的激励函数

隐层

输出层

权系数修正公式见式（9）。将训练好的神经网络作为控制器的初始值，这样在控制初期就不会出现较大的波动。

仿真实验在Matlab的Simulink工具箱环境下进行［10］，仿真结构图如图6所示，其由两部分组成：一部分是原轧机系统，也就是图2所示的轧机二质量系统；另一部分为控制系统，其中包括电流调节器、速度调节器、前馈补偿控制器和BP神经网络状态观测器。神经网络是通过编写一个M函数实现的。仿真过程是首先以单位阶跃信号模拟轧机传动系统起动过程，然后在3 s时突加单位阶跃负载扰动模拟咬钢时轧机系统的动态变化过程，并对BP算法改进前后神经网络状态观测器控制在连接轴扭矩和负载转速的动态响应上进行比较，仿真结果曲线如图7、图8所示。

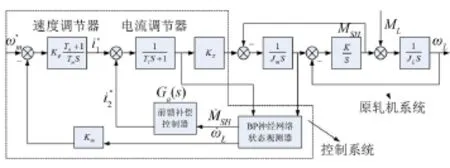
图6轧机传动仿真结构图

图7为突加阶跃时连接轴扭矩的对比曲线，其中图7（a）为算法改进前的变化曲线，图7（b）为算法改进后的变化曲线。可以明显地看到BP算法改进前的控制系统，无论是在电机起动时还是在单位阶跃负载扰动发生时，连接轴转矩振荡的都非常严重，平均振幅和频率都比较大；相比，BP算法改进后的控制系统，无论是在电机起动时还是在单位阶跃负载扰动发生时振荡都明显减轻，平均振幅和频率明显减小。

图8为突加阶跃时负载转速的对比曲线，其中图8（a）为算法改进前的变化曲线，图8（b）为算法改进后的变化曲线。可以清楚看到BP算法改进前的轧机传动系统负载转速在电机起动时超调量比较大，且振荡非常严重，平均振幅和频率都比较大，调节时间比较长，当单位阶跃负载扰动发生时产生较大的动态速降；相比，BP算法改进后的系统负载转速超调量有所减少，且振荡明显减轻，平均振幅和频率明显减小，调节时间较短，当单位阶跃负载扰动发生时产生的动态速降也较小，动态性能得到明显改善。

图7　连接轴扭矩比较

图8　负载转速比较

4　结语

考虑到扭振模型比较复杂和参数不易测量的特点，在建立考虑负载转矩的轧机传动系统动力学模型的基础上，提出了基于神经网络的状态观测器，设计基于改进BP神经网络状态观测器的智能控制系统，并利用simulink对轧机实例进行仿真。通过比较可以明显看出，无论是轧机起动过程还是在单位阶跃负载扰动发生时的恢复过程，引入基于改进BP神经网络状态观测器的控制后，系统的动态性能明显改善，连接轴转矩振荡明显减小，扭振现象得到显著抑制。结果表明设计的智能控制系统对轧机传动系统的扭振有良好的控制效果。

［1］李崇坚，段巍.轧机传动交流调速机电振动控制［M］.北京：冶金工业出版社，2003.

［2］SUN Xiao-dong，CHEN Long，YANG Ze-bin，et al.Speed sensorless vector control of a bearingless induction motor with artificial neural network inverse speed observer［J］. IEEE Transactions on Mechatronicsl，2013，18（4）: 1357-1366.

［3］Luis E.Zarate，Sergio M.Dias.Qualitative behavior rules for the cold rolling process extracted from trained ANN via the FCANN method［J］.Engineering Applications of Artificial Intelligence，2009，（22）:718-731.

［4］米江，纪国宜.改进的BP神经网络在风机故障诊断中的应用［J］.噪声与振动控制，2011，31（2）：94-98.

［5］TeresaOrlowska-Kowalska，MarcinKaminski. Application of the OBD method for optimization of neural state variable estimators of the two-mass drive system［J］. Neurocomputing，2009，20（1）:3034-3045.

［6］张瑞成，童朝南.基于状态观测器的轧机主传动系统机电振动控制研究［J］.电气传动，2005，35（11）：1005-1009.

［7］ZHAI lian-fei，CHAI tian-you.Nonlinear decoupling PID control using neural networks and multiple models［J］. Journal of Control Theory and Applicationgs，2006，（1）: 62-69.

［8］孟宗，高海滨，刘彬.基于小波神经网络的轧机接轴扭振状态识别研究［J］.仪器仪表学报，2006，27（6）：1724-1725.

［9］孙玉国，尹玉川.机器基础动力耦合系统最优控制器设计与性能仿真［J］.噪声与振动控制，2003，23（3）：24-26.

［10］闻新，周露，王丹力，等.MATLAB神经网络应用设计［M］.北京：科学出版社，2001.207-232.

Intelligent Control of Torsional Vibration of Rolling Mills Based on Improved BPNeural Network

SHI Pei-ming，LI Bing-yang
（College of Electrical Engineering，Yanshan University，Qinhuangdao 066004，Hebei China）

The dynamic model of the drive system of rolling mills was established to study the torsional vibration control problem in the loading condition.Due to the complicated characteristics and the difficulty in parameters measurement of the torsional vibration model，the state observer method was proposed based on neural network，and the typical BP network was optimized.The intelligent control system based on the improved BP neural network observers was designed and the real mill examples were simulated using SIMULINK.The results show that the designed smart control system of the rolling mill drive system has a good effect for torsional vibration control.

vibration and wave；transmission system of the rolling mill；torsional vibration；improved BP neural network；state observer

TM341；TH113.1

ADOI编码：10.3969/j.issn.1006-1335.2015.05.028

1006-1355（2015）05-0134-05

2014－11－25

河北省自然科学基金（E2012203194）；河北省高等学校创新团队领军人才培育计划项目（连铸、轧钢自动化技术及应用）（LJRC013）

时培明（1979－），男，黑龙江哈尔滨人，副教授，主要从事轧机振动控制等方面的研究工作。

E-mail:spm@ysu.edu.cn