利用RTK进行多波束水深测量时GPS高程数据的处理

刘福刚

(中石化石油工程设计有限公司，山东 东营　257000)



利用RTK进行多波束水深测量时GPS高程数据的处理

刘福刚

(中石化石油工程设计有限公司，山东 东营257000)

利用RTK进行多波束水深测量时，GPS高程在提供瞬时垂直基准方面起着重要的作用。海上实际作业过程中，GPS信号经常会发生失锁现象,造成部分历元高程数据突变，导致海底地形失真。该文以茂名某项目为例，首先介绍了根据EGM2008大地水准面模型，利用高程拟合法将多波束水深测量时GPS椭球高转换为正常高的方法；然后针对GPS信号失锁现象，提出了利用RTK高程中的固定解来求算海水潮位面的方法，同时阐述了该方法的优势。

RTK；水深测量；多波束；椭球高；正常高;高程数据处理

引文格式：刘福刚.利用RTK进行多波束水深测量时GPS高程数据的处理[J].山东国土资源，2015，31(9)：90-93.LIU Fugang.Elevation Data Processing of GPS in Multibeam Bathymetric Measuring by Using RTK Technology[J].Shandong Land and Resources,2015，31(9)：90-93.

0　引言

多波束测深系统是水声、计算机、导航定位和数字化传感器等多种技术的高度集成。是利用安装于船底或拖体上的声基阵向与航向垂直的海底发射超宽声波束，接收海底反向散射信号，经过模拟/数字信号处理，形成多个波束，同时获得几十个甚至上百个海底条带上采样点的水深数据。其测量条带覆盖范围为水深的2～10倍，与现场采集的导航定位及姿态数据相结合，能够绘制出高精度、高分辨率的数字成果图。与单波束回声测深仪相比，多波束测深系统具有测量范围大、测量速度快、精度高的优点。

对发射声波瞬间换能器的定位、定姿是多波束水深测量的重要一步。目前，可利用差分GPS(DGPS)系统或RTK的方式求出换能器平面位置，利用电罗经、姿态传感器求出换能器瞬时姿态，定位定姿中的导航延时、横摇、纵摇、艏偏通过检校场检校计算得出。传统多波束测量中，换能器瞬时高程是由潮位、吃水参数和涌浪参数(Heave)联合提供，理想条件下，该高程是准确无误的。但是实际测量过程中，潮位是由测区多个验潮站数据线性内插得到，吃水参数易受船速等因素影响，Heave在船速突变时会有长周期信号异常，使得计算出的换能器瞬时高程值精度大受影响[1]。

GPS-RTK定位技术是基于载波相位观测值的实时动态定位技术。在RTK解固定时，通过量测、计算GPS天线相位中心与换能器间的相对关系，能实时求出换能器瞬时高程。

在已知GPS天线高程的情况下，只需量测GPS天线位置到换能器之间的高差值h1，便可求出换能器瞬时高程，从而消除了潮位模型选择、动态吃水测量不准确及船速突变时Heave异常带来的影响(图1)。

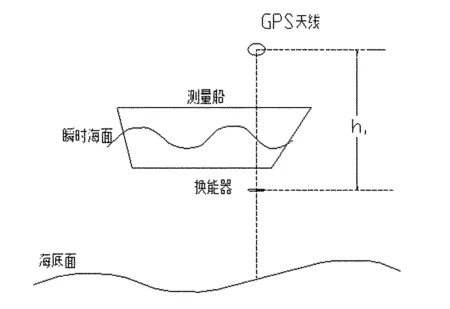
图1　GPS接收机天线与换能器相对位置示意图

1　工程应用

茂名某海洋测量项目，由岸边往海中东南方向延伸约15km，水深20m左右，需要测量管线两侧各250m内水下地形。项目采用WGS-84 坐标系统(UTM投影)，1985国家高程基准。该次采用设备有天宝GPS 2台、Geo Swath Plus多波束测深系统(250Hz)和处理软件GS+。

GPS测得的是点位的椭球高，工程需要的是该点的正常高，两者间的差值(高程异常)不是一个常数。同时海上作业过程中经常出现失锁现象，GPS信号失锁部分的高程无法利用。以该项目为例介绍椭球高到正常高的转换方法及利用GPS高程计算潮位数据的方法来消除GPS信号失锁的影响。

1.1GPS椭球高到正常高的转换

椭球高到正常高的转换，一般有2种方法：

1.1.1七参数法

测区范围内取3个以上已知控制点，通过输入已知点的WGS84坐标及当地坐标，求出3个平移参数、3个旋转参数及1个尺度比参数，从而在2个椭球间建立联系，实现由椭球高到正常高的转换。此方法要求测区在已知控制点范围内或边缘，不要超出控制区域太远，否则得出的高程值不具可信性。同时，该方法无法处理测区内高程异常值凹下或凸起的区域。

1.1.2高程拟合法

在传统的大地测量中,高程异常是通过重力测量和天文测量的方法确定的,但对大多数测量单位来说,并不具备这2种作业的条件。目前国内外常用的方法是采用数学拟合的方法[2]。

通过EGM2008大地水准面模型，结合模型内不同点的高程异常，以线性内插的方式求出待测点高程异常值，从而实现椭球高到正常高的转变。此方法在测区周围控制点不多或不能有效覆盖测区时，可以获取高可靠性的RTK高程。同时，该方法降低了测区范围内局部地区高程异常值凹下或凸起带来的危害。 由于海上作业的一侧是海洋，很难搜集到覆盖测区的控制点资料，在采用RTK测量海深的作业模式上，不推荐用七参数法。该次文采用高程拟合法。图2为该次作业GS+导出的某条测线的部分导航数据。

图2　某测线的部分导航数据

图2第一行中的“4”表示固定解，“17.777”表示正常高，“-10.323”表示大地水准面差距，两者之和为椭球高。此处的大地水准面差距是由集成在GPS接收机中粗略的大地水准面模型得出，误差较大，同时GS+的算法较简单，在每条测线只取了1个大地水准面差距值。因此需要对导航数据进行后处理，以便求出正确的正常高。

基本思路为：首先利用公式H=h+ζ(式中H代表该点椭球高；h代表该点正常高；ζ代表该点高程异常，下同)，恢复椭球高H，然后根据EGM2008模型查找测量点位区域内四周点的ζ值，利用线性内插的方式求出待测点位的ζ值，最后利用公式h=H-ζ求出待测点位的正常高。

理论上，要求得测量点位的正常高，有如下两种方法可用：

方法一：直接法。要想求得点2的正常高，利用该点的椭球高直接减去该点的高程异常值，公式为：

(1)

方法二：间接法。若要求得点2的正常高，利用已知点1的正常高加上两者间椭球高的差再减去两者高程异常的差，公式为：

(2)

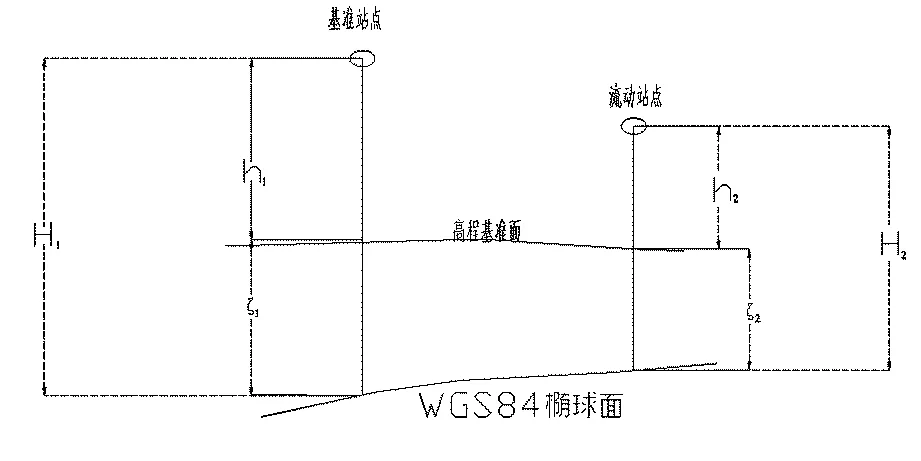
图3　基准站点、流动站点椭球高与正常高关系图

如图3所示，公式(1)(2)中h2为RTK测量点位正常高；h1即为已知点(基准站点)正常高；H1为基站点椭球高；H2为导航数据中正常高与大地水准面差距的和；ζ1，ζ2由选用的EGM2008模型求得(公式中的正常高、椭球高、在实际工作中要考虑仪器高、天线高等)。

方法一得出的正常高为EGM2008高程基准，要想得出1985国家高程基准的正常高，还需减去两者间的差距。另外，该方法需准确搜集到已知点的高精度WGS-84坐标(B，L，H)。方法二消除了WGS84坐标H绝对精度低及2个高程基准面差距的影响，实际工作中主要应用此方法。

该项目15km测区内，Δζ(ζ2—ζ1)从岸边(基准站)往测区深处基本呈线性逐步增大，在5km处值约为16cm，在10km处约为34cm，在15km处约为46cm。Δζ通常情况下表现为使测区海底倾斜，离基站越远，倾斜(误差)程度越深。因为它是一个系统误差，通过布设重合、交叉测线的方式无法将其检测出来。所以在用RTK结合多波束进行水深测量时，一定要考虑Δζ的影响。

1.2RTK高程计算潮汐数据

实际海上测量中，受风浪、船体操纵等影响，GPS信号会出现失锁现象，此时的GPS高程不能直接利用。目前，国内主要研究采用对GPS高程数据进行修正的方式来确保GPS高程数据的质量，修正后的GPS高程数据直接用于求算换能器瞬时高程。其中常见的有Kalman滤波、Heave修正等。

项目中，首先利用GPS高程求算随船移动的潮位面数据，然后根据潮位面数据去求算换能器瞬时高程。

1.2.1GPS高程常用修正法

Kalman滤波法：Kalman滤波是一种对动态测量数据实施滤波的常用方法，随着观测数据的增加，状态估计应愈来愈精确。但在实际应用中，当GPS观测存在连续异常时，则采用传统的Kalman滤波易出现发散问题[3]。

Heave修正法：Heave修正法利用的是正常的GPS高程时序和Heave时序反应的都是船体的垂直运动，在短时间内应该具有一致性的原理通过姿态传感器测得的Heave值来对GPS高程进行修正。但是，Heave具有零均值特征,其变化反映的是船体的高频运动特征,无法表现船体的全周期垂直运动,即潮位、波浪和船体操纵等产生的综合垂直运动；GPS高程序列不但可以呈现船体的瞬时变化,还可以呈现其中、长周期垂直运动波。因此，Heave对GPS RTK高程的修正只能在短时间段内进行。根据潮位、波浪和船体操纵的周期特征，这种修正的有效时间段最长不能大于2min[4]。

经过修正后的GPS高程数据直接用于求算换能器瞬时高程。得出的高程起着提供瞬时垂直基准的重要作用,每个历元的观测数据均须可靠稳定,否则将会引起水下地形的异常[4]。因此,该方法要求GPS原始数据信号失锁时间不能太长，同时处理过程中对GPS高程成果的质量要严格把控。

1.2.2利用RTK高程求算潮位数据文件

鉴于该项目多条测线出现了持续2～3min的RTK浮点解或单点解数据，利用Kalman滤波、Heave修正无法消除GPS失锁对水深成果造成的影响，提出了另一个思路。利用GPS中的固定解数据反算海平面，得到一个“架设在船上的验潮站”潮位文件，并利用该文件结合涌浪参数及吃水求算换能器瞬时高度。

求算潮位文件的过程为： 首先，划分一个合理的时间段。该时间段要包含多个涌浪周期(Heave-Bandwidth)及足够多的高程数据，同时考虑2次失锁情况，该周期不能过大。该项目GPS输出频率为20Hz，涌浪周期为7S左右，每个周期内GPS输出140次，1 min内输出1200次，该时间段(区间)设置为1min。

其次，设置区间内有效数据阈值。设置区间内GPS固定解的数量的阈值为x，如果固定解数量小于x，则将该区间内所有数据舍弃；否则保留该区间数据。该项目处理过程中在将区间段设置为1 min的情况下，该阈值设置为1000。失锁严重的测线，也可将该值适当缩小，并对该时间段内潮位文件进行人工检核。

最后，计算该区间时刻海水潮位面。经过第二步的过滤后，将每个区间内所有固定解高程取平均，结合天线高及换能器吃水值，从而得出该区间时刻海水潮位面数据。

获取海水潮位面的目的是为了求算换能器高程，所以在第三步中，也可结合GPS天线与换能器的高差(图1中的h1)，直接求算“换能器潮位面”数据。

2　结论

与传统验潮方法相比，利用RTK进行多波束水深测量在高程获取方面是完全不同的一种方法。该文通过茂名某海洋测量项目为例，针对高程转换及RTK信号失锁情况，在GPS高程数据处理方面，提出了以下几个建议：

(1)GGA原始数据中的大地水准面差距值是由内置在GPS接收机中粗略的大地水准面模型给出，误差较大，要想得出高精度水深数据，首先要恢复点位的椭球高。

(2)在GPS椭球高向正常高转变过程中，优先使用EGM2008模型进行高程拟合，测区内不同点位的高程异常差值Δζ(ζ2-ζ1)在10km范围内，可达30cm以上。忽略Δζ会对测深结果产生非常大的系统差值，且简单的布设重复测线无法检测出此项误差。

(3)在测量过程中，GPS存在短时间失锁情况时，可以通过利用GPS高程数据求算潮位数据的方式，消弱失锁对成果的影响。该方法利用的是GPS高程数据里面的有效高程值，且可对生成的潮位数据图像化显示，利用海水周期性涨落的特点进行人工检核；而对GPS高程数据进行Kalman滤波、Heave修正等方法，需要修正后的每个历元的观测数据均必须可靠、稳定。所以利用GPS高程数据求算潮位数据的方法，对GPS数据质量要求更宽松，求算出的水深结果更可靠。

综上所述，利用提出的对RTK-GPS高程数据的处理，可以求算随船移动的潮位面数据，降低了短时间内GPS信号失锁对多波束水深测量数据的影响。

[1]阳凡林，赵建虎，张红梅，等.RTK高程和Heave信号的融合及精度分析[J].武汉大学学报信息科学版,2007，32(3):225-228.

[2]程海帆,冷曦晨,郭宝君. GPS高程两种拟合方法在山区公路勘测中的应用研究[J].公路交通科技，2008,25(9)：336.

[3]暴景阳,刘雁春.海道水位控制方法研究[J].测绘科学,2006,31(6):49-51.

[4]张红梅，赵建虎. 精密多波束测量中GPS高程误差的综合修正法[J]. 测绘学报,2009，38(1):24-26.

Elevation Data Processing of GPS in Multibeam Bathymetric Measuring by Using RTK Technology

LIU Fugang

(Sinopec Petroleum Engineering Corporation， Shandong Dongying 257000, China)

In the period of measuring multi-beam by using RTK technology, GPS elevation plays an important role in providing instantaneous vertical datum. During the actual operation process in the sea, GPS signals often happen the problem of out of lock. It will cause mutations of some epoch elevation data, and distortion of submarine topography. In this paper, setting Maoming project as an example, according to EGM2008 geoid model, by using elevation fitting method, in the process of measuring multibeam bathymetric, GPS ellipsoidal height will convert to normal height. Then pointing to the phenomenon of losing and locking GPS signals, the method of using elevation fixed solution to calculate sea tide surface by using RTK technology has been put forward. The advantages of this method have been explained as well.

RTK；multibeam； ellipsoid height； normal height; elevation data processing

2015-06-24；

2015-07-31；编辑：陶卫卫

刘福刚(1983—)，男，山东昌乐人，工程师，现从事海洋测量方面的研究;E-mail:slecclfg@163.com

P228.42

B