三维编织复合材料热传导性能研究

张　琳，李嘉禄

(天津工业大学，天津 300387)

三维编织复合材料热传导性能研究

张琳，李嘉禄

(天津工业大学，天津 300387)

文章运用热传导系数仪研究了三维编织复合材料热传导性能，分析了编织角(α)、纤维体积含量变化对其热传导性能的影响，并对比了三维四向编织复合材料(4D)、三维五向编织复合材料(5D)和层合复合材料的热传导性能。

热传导系数； 三维四向编织复合材料； 三维五向编织复合材料； 层合复合材料

三维编织复合材料作为近年来发展的高性能新型结构材料，相比传统层合复合材料，具有更优异的性能，在航空、航天等领域得到了越来越广泛的应用。随着工程技术的发展，对复合材料热物理性能的研究逐渐得到了人们的重视。热传导性能是复合材料的一个重要指标，只有对复合材料的热传导性能有足够的认识，才能将复合材料很好地应用于热环境中。

目前国内外都有关于复合材料热传导性能的研究。轰荣华等[1]理论分析模型采用的理想单胞模型能较好地预测二维编织C/SiC复合材料的等效热传导系数。程伟等[2]研究了单向复合材料和机织复合材料的热物理性能，并利用“米”字型枝状胞体有限元模型，计算了4D材料的导热性能。刘振国等[3～5]基于更加真实的胞体结构模型，研究了4D材料的热传导性能，给出的理论预测与实验值吻合得较好。李典森等[6]建立了5D编织复合材料的有限元模型,结合4D编织复合材料的有限元模型计算得到了5D和4D编织复合材料横向和纵向热传导系数。皮秀标等[7]受文献[8]的启发，也对全5D材料的细观结构进行了分析，推导了编织角等工艺参数与胞体结构参数间的数学关系。夏彪等[9]采用周期性非绝热温度边界条件和周期性位移边界条件，计算了4D材料和5D材料的整体等效热传导系数和热膨胀系数，所得结果同已有文献相比与实验值符合得更好些。王成禹等[10]基于ANSYS的APDL语言编程建立了全5D编织复合材料的参数化有限元模型，并对其弹性性能和热物理性能进行了有限元分析，得到了弹性常数、热传导系数和热膨胀系数随编织角和纤维体积含量的变化规律。Soheil[11]对三维编织复合材料的热膨胀性能进行了系统的研究，利用有限元方法预测了三维编织复合材料的热膨胀系数[12]。Yang等[13]采用修正的经典层合板理论对4D材料的刚度性能进行了研究。

1　实验

1.1试件

本论文采用的试件是碳纤维/环氧树脂三维五向编织复合材料、三维四向编织复合材料和层合复合材料。

1.1.1三维五向编织复合材料

预成型件均采用四步法三维1×1方型编织工艺，在天津工业大学复合材料研究所的三维编织机上编织完成。编织所用纤维为T700-12K的碳纤维，密度1.76 g/cm3，线密度0.8 g/m。根据测试方案设计，三维五向编织预成型件共9组，每组3片。在所需结构参数(表面编织角、纤维体积含量等)的基础上，其它编织工艺参数的计算参考三维五向编织物的基本工艺设计方法。

1.1.2三维四向编织复合材料

预成型体在天津工业大学复合材料研究所的三维编织机上采用四步法1×1三维四向编织工艺编织而成。编织纱为的T700-12K碳纤维，密度1.76 g/cm3，线密度0.8 g/m。根据实验要求，9组用于测试的三维四向编织复合材料试件每组3个试片。

2018年9月15日，第二十四次全国地方立法工作座谈会在浙江杭州召开。中共中央政治局常委、全国人大常委会委员长栗战书出席会议并讲话。他强调：“要以习近平新时代中国特色社会主义思想和党的十九大精神为指导，总结改革开放40年来我国立法工作特别是地方立法工作的成就和经验，推动地方立法工作与时代同步伐、与改革同频率、与实践同发展，为完善中国特色社会主义法律体系、推动地方经济社会发展作出新贡献。”

1.1.3层合复合材料

层合复合材料试件采用T700-12K碳纤维平纹布，面密度为500 g/m2。试验用层合复合材料试件中，纤维的取向为30°、40°、45°和90°，为了满足纤维体积含量的需要，层数分别为7层、8层和9层。

1.2实验装置

1.2.1TC3000热传导系数仪

热线法热传导系数仪TC3000主要包括测试主机、传感器、标准试样和测试软件Hotwire 3.0，如图1所示。

图1　TC3000热传导系数仪

1.2.2瞬态热线法原理

瞬态热线法是利用测量热丝的电阻来测量物质热传导系数的，基于1976年Healy JJ提出的理论，其理想模型为：在无限大的各向同性、均匀物质中置入直径无限小、长度无限长、内部温度均衡的线热源，初始状态下二者处于热平衡状态，突然给线源施加恒定的热流加热一段时间，线热源及其周围的物质就会产生温升，由线热源的温升即可得到被测物体的热传导系数。其控制方程是简单的傅里叶方程：

式中：T为温度，

t为时间，

a为被测物质的热扩散系数，a=λ/ρCP，λ为被测物质的热传导系数，ρ与CP分别为被测物质的密度和定压比热容。

1.2.3试样要求

对于块状或片状样品，需要准备两块相同材质的样品；样品的最小厚度不能低于0.3 mm，最小直径为20 mm，当样品的热传导系数较大时，样品的最小厚度需要随之增加；两块试样尺寸可不一致、边界可不规则，但与传感器的接触面需尽量保持平整光滑。

1.2.4试验过程

相同参数的三个试样为一组，每两块进行一次测量，具体过程如下：

取其中一块试样置于桌面(或者环境模块内腔)。将传感器探头放样上,保持探头平整。探头不能偏离试样。将另一块试验样品完全覆盖在探头上，两块样品不得偏离探头，不能将探头露于试样之外。确保样品和探头表面之间无空间隙，因为空气间隙可能导致样品过热或损坏探头。用带有一定质量的物品(可选配配套的500 g砝码)压住试样和探头。如有环境模块，需将环境模块前门关合，接通电源，使用软件端进行温度控制。

2　实验结果与讨论

在实验中分别对不同编织角、不同纤维体积含量的三维四向编织复合材料、三维五向编织复合材料和层和复合材料进行了热传导性能的分析(每3个相同的试件为一组)，获得了各个热传导系数平均值，见表1、表2、表3，并分别以编织角和热传导系数为变量做成了折线图，如图1、图2、图3所示。

图1描述了层合复合材料取向角和纤维体积含量对复合材料热传导系数的影响。从图1中可以明显看出当取向角一定时，热传导系数随着层数增加而增大；当层数一定时，热传导系数又随着取向角的增大而增大。这主要是因为取向角增大时,将导致试件横向上的纤维比例增大,而纤维的热传导系数大于基体,所以使得整个复合材料的横向热传导系数得以提高。同样纤维体积含量增大，从而热传导系数增加。

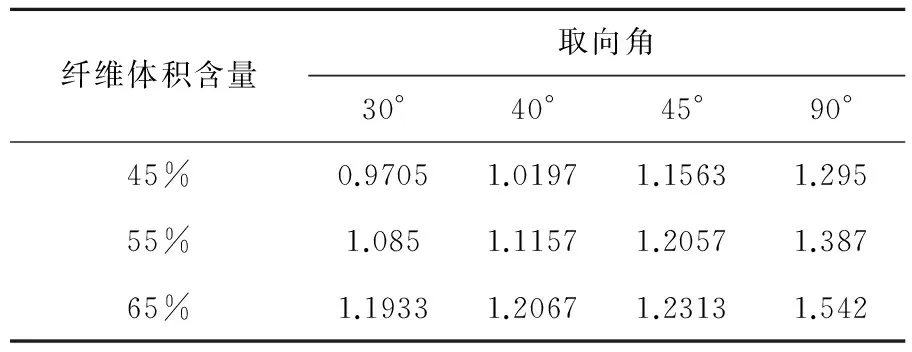
表1　层合复合材料热传导系数

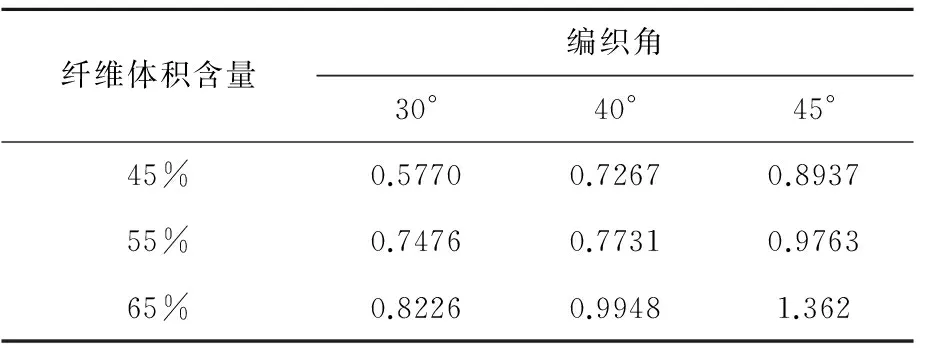
表2　三维四向编织复合材料热传导系数

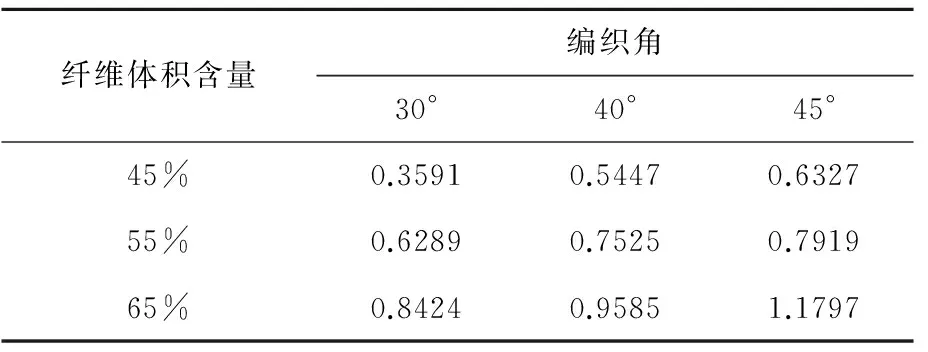
表3　三维五向编织复合材料热传导系数

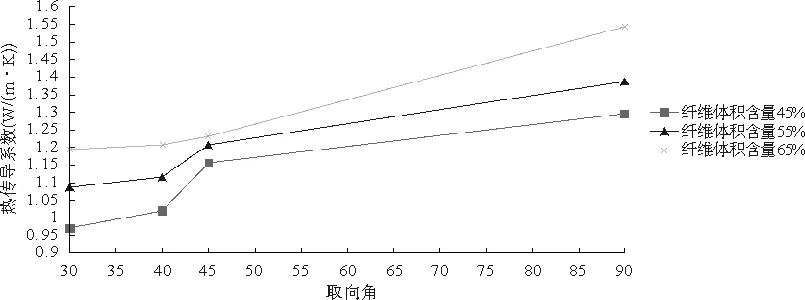
图1　层合复合材料的热传导系数

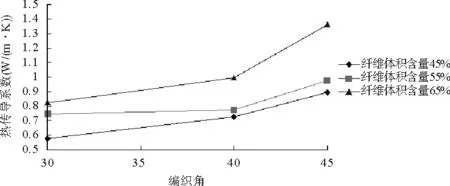
图2　三维四向编织复合材料的热传导系数

由图2可以看出，当纤维体积含量一定时，三维四向编织复合材料的热传导系数随编织角增大而增大；当编织角一定时，三维四向编织复合材料的热传导系数随纤维体积含量增大而增大。

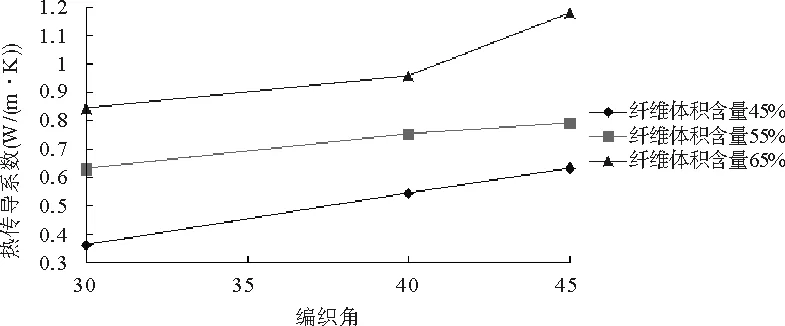
图3三维五向编织复合材料的热传导系数

三维五向编织复合材料在纤维体积含量一定时，热传导系数随编织角增大而增大；在编织角一定时，热传导系数随纤维体积含量的增大而增大，如图3。

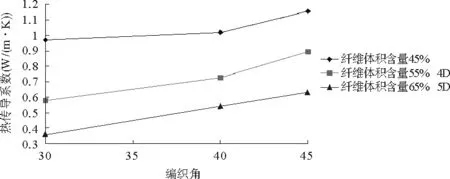
图4　编织角和纤维体积含量与4D、5D材料热传导系数关系

图4描述了编织角和纤维体积含量与4D、5D编织复合材料的热传导系数的关系。从图中可以明显看出，当纤维体积含量一定时,5D复合材料和4D复合材料的热传导系数都随编织角的增加而增大。这主要是因为编织角增大时,将导致试件横向上的纤维比例增大,而纤维的热传导系数大于基体,所以使得整个复合材料的横向热传导系数得以提高。而5D复合材料由于加入了轴纱,大大提高了纵向上纤维的含量,造成横向上的纤维比例比4D材料要小,从而导致热传导系数比4D材料要小。从图中还可看出，当α较小时,5D和4D材料的纤维大都集中在纵向上,在横向上的纤维比例都较小,从而使得两种材料的热传导系数比较接近。而随α的增大,相对5D材料,4D材料在横向上的纤维比例要逐渐增大,使得两种材料横向热传导系数的差距也逐渐增大。

三维编织复合材料与层合复合材料相比，当纤维取向相同时，层合复合材料的纤维体积含量比编织复合材料大，导致层合复合材料比三维编织复合材料热传导系数大。

3　结论

3.1对于层合复合材料，其热传导系数随着纤维体积含量的增加而增加;且当纤维体积含量一定时，热传导系数随着取向角的增大而增大。

3.2对于三维四向和三维五向编织复合材料，当编织角一定时，热传导系数随着纤维体积含量的增大而增大。

3.3对于三维四向和三维五向编织复合材料，在其他条件一定时，热传导系数同样随着编织角的增大而增大。

3.4编织角和纤维体积含量一定的前提下，三维五向编织复合材料的热传导系数要比三维四向编织复合材料的热传导系数小。

3.5在纤维的取向角度一定的情况下，层合复合材料比三维编织复合材料的热传导系数大。

[1]轰荣华,矫桂琼,王波.2D编织C/SiC复合材料厚度方向热传导系数预测[A].第十五届全国复合材料学术会议论文集[C]，2008：388—394.

[2]程伟，赵寿根，刘振国，等．三维四向编织复合材料等效热特性数值分析和试验研究[J]．航空学报，2002，23(2)：102—105.

[3]刘振国．三维全五向编织预型件的概念[J]．材料工程，2008，(S1)：305—312.

[4]Zhang F，Liu Z G，Wu Z H，et al.A new scheme and microstructural model for 3D full 5-directional braided composites [J]．Chinese Journal of Aeronautics,2010, 23(1): 61—67.

[5]Liu Z G，Zhang H G，Lu Z X．Investigation on the thermal conductivity of 3-dimensional and 4-directional braided composites [J]．Chinese Journal of Aeronautics,2007,20(40):327—331.

[6]李典森，卢子兴，刘振国，等．三维五向编织复合材料导热性能的有限元分析[J]．航空动力学报，2008，23(8)：1455—1460．

[7]皮秀标，钱坤，曹海建，等．三维全五向编织复合材料的细观结构分析[J]．宇航材料工艺，2011，41(6)：39—43．

[8]刘振国．三维全五向编织预型件的概念[J]．材料工程，2008，(S1)：305—312．

[9]夏彪，卢子兴．三维编织复合材料热物理性能的有限元分析[J]．航空学报，2011，32(6)：1040—1049.

[10]卢子兴，王成禹，夏彪.三维全五向编织复合材料弹性性能及热物理性能的有限元分析[J].复合材料学报，2013, 6(3)：30—32.

[11]Soheil M，Predictions for coefficients of thermal expansion of three-dimensional braided composites[J]．AIAA Journal,1997,35(1):141—144.

[12]Soheil M．Predictions for coefficients of thermal expansion of three-dimensional braided composites [J]．AIAA Journal,1997, 35(1):1 41—144.

[13]Yang J M，Ma C L，Chou T W．Fiber inclination model of Three-dimensional textile structural composites[J]．Journal of Composite Materials,1986, 20(5):472—484.

Research on Thermal Conductivity of Three-Dimensional Braided Composites

ZhangLin,LiJialu

(Tianjin Polytechnic University,Tianjin 300387, China)

The thermal conductivity properties of three-dimensional braided composites were studied. The effects of braiding angle and fiber volume fraction on the thermal conductivity properties were researched. The thermal conductivity properties between three-dimension-four- direction braided composites, three-dimension-five-direction braided composites and laminated composites were compared.

thermal conductivity coefficient; 4D braided composites; 5D braided composites; laminated composites

2015-07-27

张琳(1989—)，女，天津人，硕士研究生。

TS105

A

1009-3028(2015)05-0050-04