新型叠加系统均力机理的数值模拟分析

韦铁平，杨晓翔，姚进辉，许　航

新型叠加系统均力机理的数值模拟分析

韦铁平1，杨晓翔1，姚进辉2，许航2

（1.福州大学机械学院，福建福州350116；2.福建省计量科学研究院，福建福州350003）

附加侧向力是引起叠加系统旋转效应的重要原因。基于有限元法（finite element method，FEM），分别对新型叠加系统均力结构的4个尺寸变量进行数值模拟分析。结果表明：在一定范围内，随着均力板惯性矩、厚度和轴承座高度增加，力传感器所受侧向力波动量减小；均力板的弹性模量在150GPa附近，力传感器获得较小的侧向力波动量。由此可知，特定的均力结构能有效抑制附加侧向力。

叠加系统；旋转效应；有限元法；均力结构；附加侧向力

doi：10.11857/j.issn.1674-5124.2015.09.025

0　引言

高准确度测力仪在检定中由于寄生分量的作用，测力仪结构的不对称性（包括机械和电性能）使得测力仪在不同的方位上示值发生改变，引起旋转效应。对于高准确度测力仪，旋转效应对其不确定度评估影响很大［1］。

为了减小力传感器的旋转效应，许多研究人员对其结构做了大量的改进工作。Kang D I等［2］通过实验验证弯矩补偿可以有效削弱叠加系统的旋转效应；Cruz J等［3］根据G.Barbato的方位原理设计了额定量程为600 kN的叠加系统，通过加大均压板厚度，减小其变形量来削弱寄生分量，从而降低旋转效应的影响；G.Barbato［4］和倪守忠［5］对板环式传感器的旋转效应做了分析，认为通过控制贴片的位置误差可以减小传感器的旋转效应；Park Y K等［6］对叠加系统不同方位进行测量，通过3个力传感器输出信号的差异来获得侧向力分量，并以此来评估叠加系统的复现性；Andrae J等［7］为了抑制寄生分量对传感器的影响，研制了轴对称结构梁式负荷传感器并提出在线补偿的方法。但采用有限元法研究叠加系统旋转效应的检测尚未进行过相关报道。

1　均力结构的受力分析

在工程实际检测和校准中，力传感器不可避免地发生旋转效应。新型叠加系统在原来的基础上增加了均力结构［9］，该结构能有效削弱旋转效应，其结构如图1所示。均力结构由均力板、定位套及固定在均力板上、下的两组推力关节轴承组成。与传统的点-面接触方式不同，定位套与力传感器之间为面-面接触。

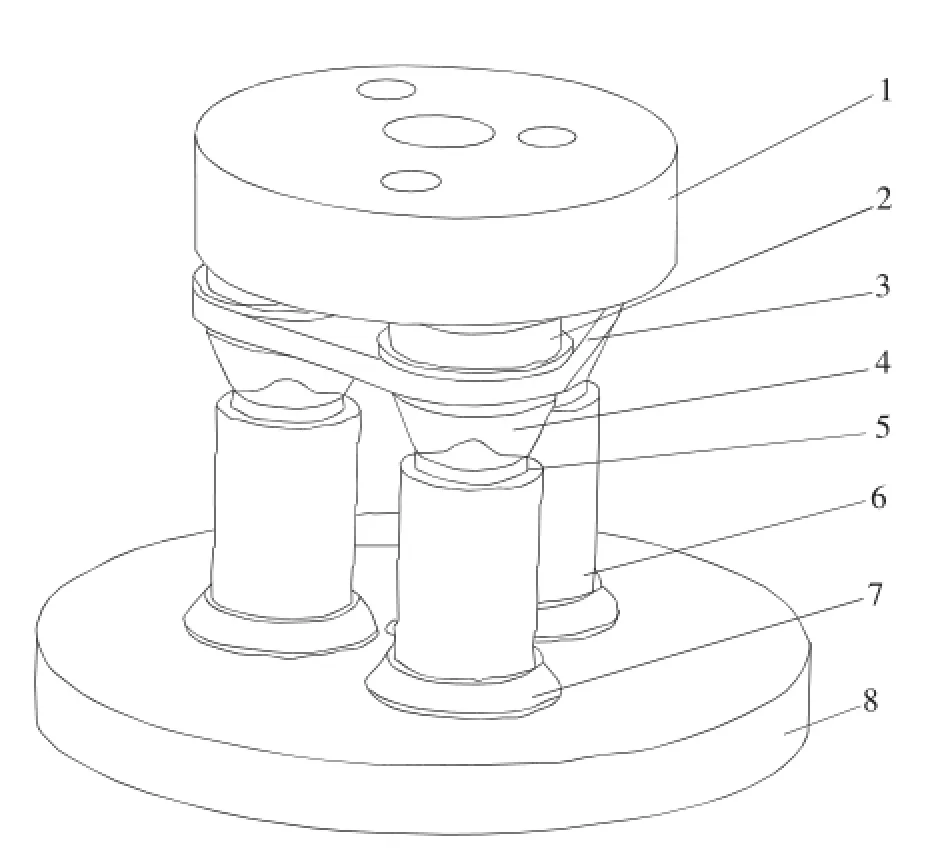
图1　叠加系统结构示意图

在检测过程中，均力板上方的推力关节轴承除了受到竖直方向上的分力FV，i（i=1，2，3），还有水平方向的附加侧向力FH，i。3个轴承所受的附加侧向力大小不均，方向不同。但在均力板的作用下，3个水平侧向力在相互耦合后能较均匀地作用在3个对中调节压头上。3个力传感器所受到水平方向的附加侧向力FH，j（j=1，2，3）急剧削弱，且作用点更加靠近力传感器的轴线，受力分析如图2所示。由上可知，均力板的变形对均力效果起到关键作用。

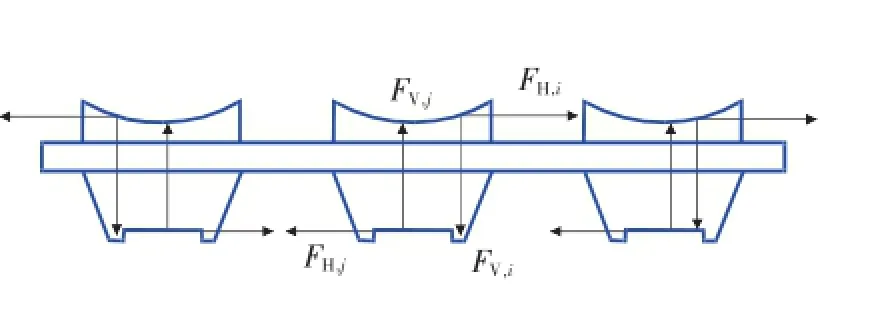
图2　均力结构受力分析示意图

叠加系统检测过程中，均力板承受垂直于中性面的力，发生的变形挠度远小于厚度，可认为是小挠度变形［10］。根据板壳理论，均力板满足平衡微分方程：

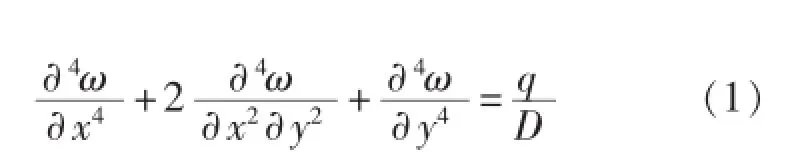
式中：ω——薄板的挠度；

q——垂直于薄板中面的载荷；

为获取均力板挠度、弯矩、扭矩和剪力的准确解，必须要知道其边界条件。均力板可作如下简化：1）对中调节压头端部简支固定；2）如图2所示，均力板不仅受到垂直于中面的载荷，同时由于轴承座高度使得水平附加侧向力产生弯矩，但是大小和方向均未知。综上分析，均力板的边界条件难以确定，无法求解微分方程的准确解。

为验证上文提出的利益协调分配机制的有效性，此部分对分散决策、集中决策以及利益协调模型中的相关参数进行赋值模拟，在满足基本假设条件的前提下，具体的参数赋值如表2所示。

为了研究均力板的均力机理，将采用有限元法模拟分析影响均力结构力学特性的4个因素：均力板的形状（惯性矩是抗弯刚度的重要影响因素）、均力板的弹性模量、均力板的厚度和轴承座高度（对均力板产生弯矩）。本文首先分析了3种惯性矩的均力板结构，获得最佳形状；在此基础上，依次对均力板的弹性模量、厚度和轴承座高度进行分析。

2　有限元模型及物理量定义

2.1均力板结构尺寸

在均力结构的研制过程中，分别设计了正方形板、类三角形板和圆形板。这3种均力板尺寸如下：1）正方形板边长为190mm；2）类三角形板由直径为190mm的圆形板沿截面AB绕着圆心阵列120°切除获得；3）圆形板外径为190mm。板厚均为6mm，中心孔径均为35mm。

根据均力板的结构尺寸可知，3种形状均力板的惯性矩大小排序为：I正方形＞I圆形＞I类三角形。

2.2有限元模型

由于对中调节压头与力传感器为面-面接触，叠加系统在检测过程中二者相对静止。根据牛顿第三定律，通过提取对中调节压头的支座反力分量即可获得力传感器所受的附加侧向力的数值大小。因此，有限元建模仅取对中调节压头及以上部件作为模拟分析对象。3个力传感器在底座上呈120°均匀分布，且结构和性能基本一致，故仅需考察其中任一力传感器的水平侧向力。

为了模拟标准机与叠加系统之间交互作用产生的寄生分量，通过引入如下非轴向试验力来实现：试验力级选择满量程300kN，力级作用点在叠加系统的轴线上，倾斜角度选取0.3°、0.5°、0.7°、1°、1.2°和1.5°共6个量值。参照ISO 376：2004（E）测力仪校准规范［11］，选择3个均匀分布的方位进行检测仅能粗略地评估旋转效应。为了获得更加准确的结果，至少选取6个方位［12］。在初始位置（设定为0°方位）检测完成后，将叠加系统绕其轴线旋转至下一个方位，依次对60°，120°，180°，240°和300°位置进行测量。由此，每个试验力均需进行6个方位模拟计算，共计108个分析模型。

利用前处理软件ANSA划分有限元网格，单元类型选择solid185，图3为圆形板的三维网格模型。材料弹性模量为210GPa，泊松比0.3。为了保证模拟结果的最佳可比性，尽量使3个有限元模型网格划分一致。除了均力板的网格，其他部件的网格大小和形状均完全相同。

图3　圆形均力板叠加系统的三维有限元网格模型

3　模拟结果与分析

3.1惯性矩对均力效果的影响

计算结果如图4所示。从图中可知，均力板惯性矩会影响均力结构的均力效果。3种均力板力传感器的附加侧向力波动量均随着倾斜角度的增加而增大；均力板惯性矩越大，力传感器的附加侧向力波动量越大。图5给出了不同均力板惯性矩产生的水平附加侧向力的平均值。由图可知，力传感器的附加侧向力平均值均随着倾斜角度的增大而增大，而平均侧向力基本一致，仅与寄生分量有关，与惯性矩无关。

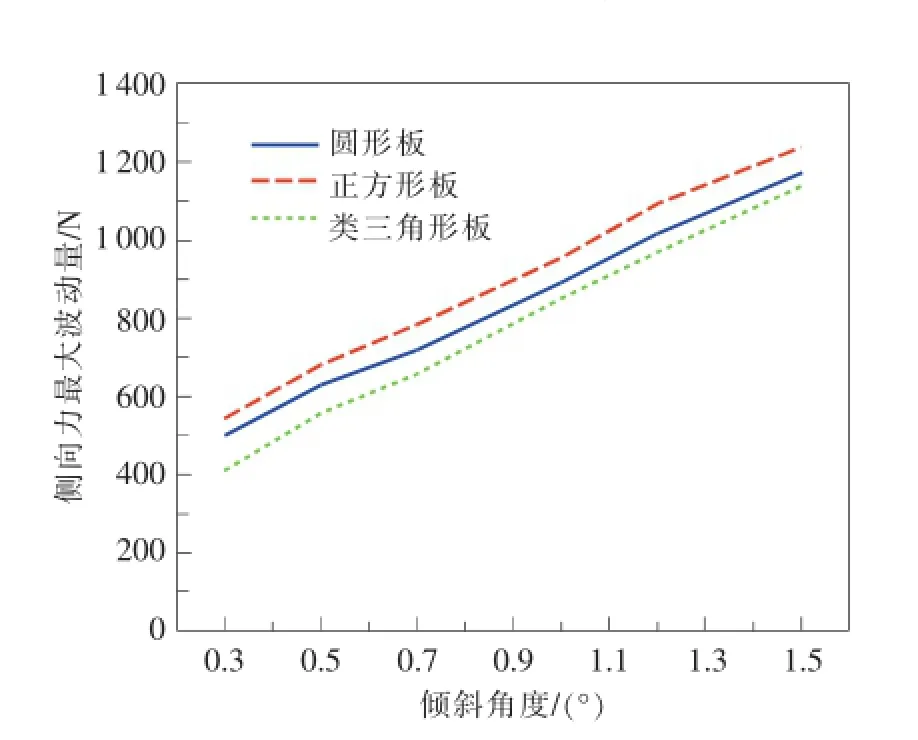
图4　均力板惯性矩对均力效果的影响

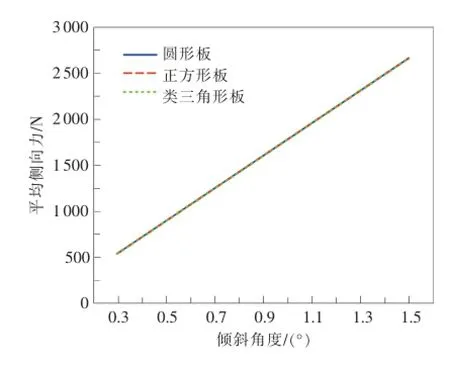
图5　不同均力板惯性矩侧向力的平均值

惯性矩较小的类三角形板有较小的测量力波动量。因此，叠加系统的研制选择类三角形板将获得最佳均力效果。

3.2弹性模量对均力效果的影响

通过选取不同弹性模量，研究均力板的材料特性对均力效果的影响。在类三角形板模型的基础上，分别设置不同的材料特性参数：泊松比取0.3，弹性模量选取60，90，120，150，180，210，240GPa 7个数值进行模拟分析，计算结果如图6所示。

图6　材料特性对均力效果的影响

从图6可知，随着弹性模量的增大，力传感器的附加侧向力最大波动量先减小后增大，最小值发生在弹性模量为150GPa附近。随着弹性模量的变化，力传感器平均附加侧向力基本保持不变。

由此可知，均力板的材料特性不会影响力传感器平均侧向力；均力板的弹性模量在150GPa附近时，均力效果最佳。综合考虑叠加系统的工作环境，材料选择球墨铸铁较为合适。

3.3厚度对均力效果的影响

为考察均力板厚度对均力效果的影响，均力板厚度分别取2，4，6，8，10，12mm 6个量值，在类三角形板模型的基础上，对类三角形板进行网格重新划分，建立有限元模型并进行模拟计算。分析结果如图7所示。

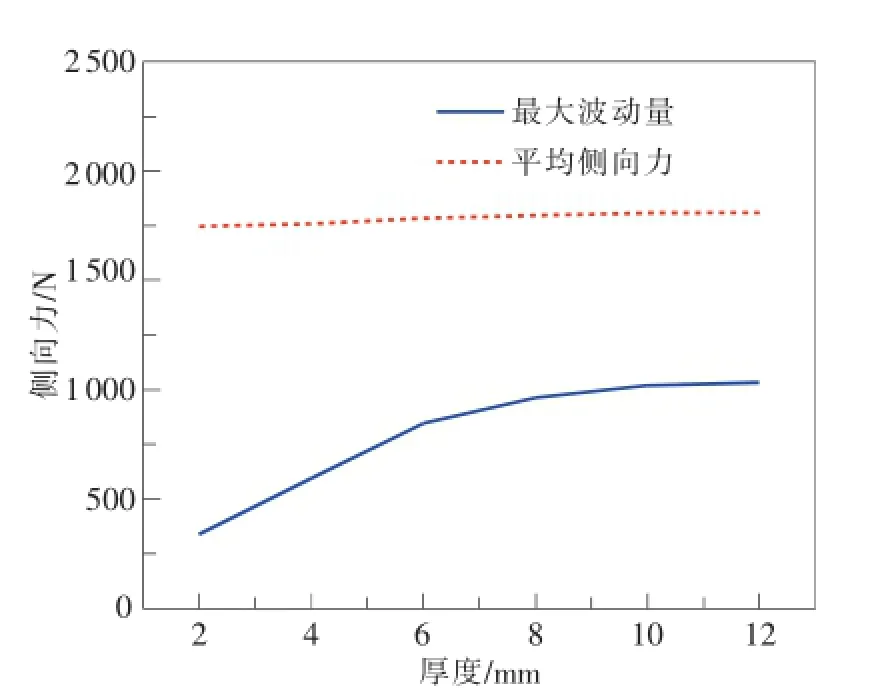
图7　均力板厚度对均力效果的影响

由图可知，随着均力板厚度的增加，力传感器所受附加侧向力的波动量逐渐增大。厚度增大到10mm以后，波动量趋于恒定值。此外，均力板厚度的增大不影响力传感器平均附加侧向力的大小。

由上可知，随着均力板厚度的增加，均力效果降低。考虑到加工准确度及叠加系统的工作环境，均力板厚度选择6mm较合适。

3.4弯矩对均力效果的影响

均力板所受弯矩的大小可通过改变轴承座的高度来调节。轴承座高度分别取2，4，6，8，10mm 5个量值。在类三角形模型的基础上，对轴承座进行网格重新划分，建立三维有限元模型并模拟计算，分析结果如图8所示。

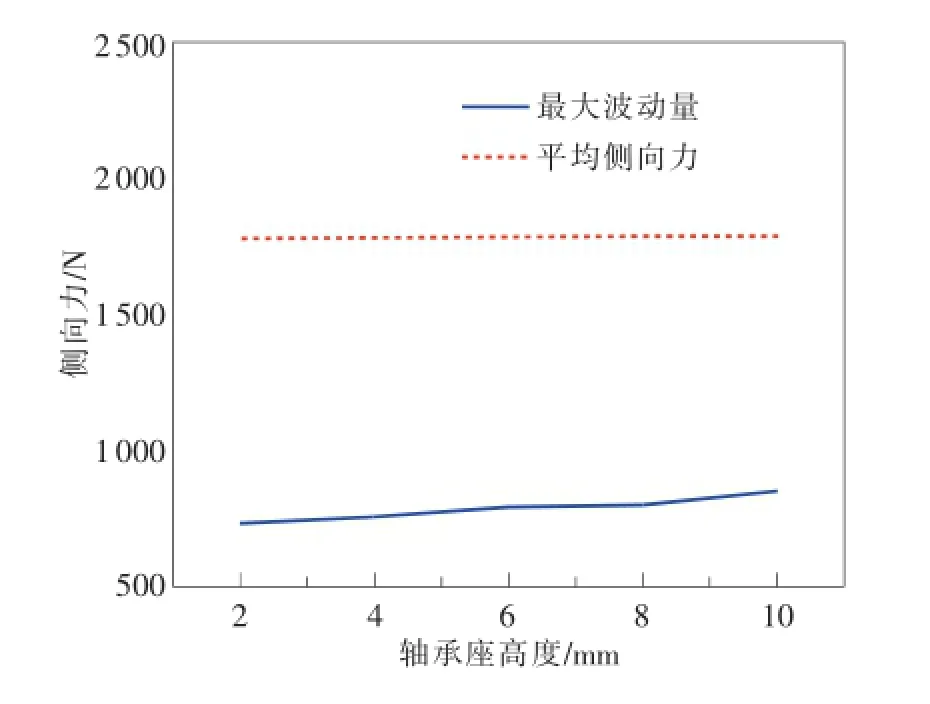
图8　弯矩对均力效果的影响

由图可知，随着轴承座高度的增加，均力板所受弯矩增大，附加侧向力波动量也逐渐增大，但改变量不大；力传感器平均附加侧向力基本保持不变。随着轴承座高度增加，均力效果变差。因此，在叠加系统的研制中，轴承座在满足定位强度的情况下，其高度越小越好。

综上4个因素的分析，寄生分量不会影响力传感器的平均附加侧向力，但对其波动量影响明显。对于不同结构形状的均力板，惯性矩越小，均力效果越好，具有最小惯性矩的类三角形板均力效果最好；均力板的弹性模量在150GPa附近时，力传感器的附加侧向力波动最小；均力板的厚度对力传感器的附加侧向力影响最显著，厚度越小，附加侧向力的波动量越小；随着轴承座高度的增加，均力板所受弯矩增加，将导致侧向力波动量增大。由此可见，均力板适量变形有利于抑制力传感器附加侧向力的波动量，从而达到均力效果。

4　结束语

本文根据均衡力传感器的受力可改进叠加系统的旋转效应，对不同均力结构尺寸的叠加系统进行数值模拟计算。分析结果表明，力传感器附加侧向力的平均值仅与试验力级有关；适量的均力板变形有利于提高叠加系统的均力效果，抑制力传感器侧向力的波动。研究结果可为叠加系统的改进提供指导依据。

［1］Peters M.Experiences and results of international comparison measurements of forces up to 1MN［J］.PTBMitteilungen，1989，99（5）：343-350.

［2］Kang D I，Hong C S.Rotation effects of force transducers on the output of a build-up system［J］.Measurement，1994，14（2）：147-156.

［3］Cruz J，Prodonoff V，Guerhard J，et al.Research development and characterization of a build-up system prototype up to 600 kN［C］∥Proc.of the IMEKO TC-3 Conf.on Force，Mass，Torque and Pressure Measurements Turkey，2001.

［4］电子称重技术与测力计量的最新进展［C］∥第十届国际计量技术联合会-力与质量计量会议论文选.蔡正平，译.北京：中国计量出版社，1986.

［5］倪守忠，杜之平，韩炜红.板环式传感器的方位误差分析及校正方法［J］.自动化仪表，1999，20（10）：30-31.

［6］Park Y K，Kim M S，Kim J H，et al.A proposal for an evaluation method of force standard machines by using build-up system［C］∥Proc.of the IMEKO TC-3 Conf.on Measurement of Force and Mass Cairo，2005.

［7］Andrae J，Hons C，Sawla A.High precision force transd ucer with new method for online compensation of parasitic effects［J］.Measurement，2003，33（2）：173-178.

［8］姚进辉.组合式负荷传感器方位误差的减小［J］.中国计量，2013（3）：38.

［9］福建省计量科学研究院.一种测力传感器结构：中国，201110449912.3［P］.2011-12-29.

［10］刘鸿文.板壳理论［M］.杭州：浙江大学出版社，1986.

［11］ISO 376—2011 Metallic materials-calibration of force proving instruments used for the verification of uniaxial testing machines［S］.Switzerland，2011.

［12］Xu C.A practical model for uncertainty evaluation in force measurements［J］.Measurement Science and Technology，1999，9（11）：1831.

Numerical simulation analysis of com pensating mechanism for new build-up system

WEI Tieping1，YANG Xiaoxiang1，YAO Jinhui2，XU Hang2
（1.College of Mechanical Engineering and Automation，Fuzhou University，Fuzhou 350116，China；2.Fujian Province Institute of Metrology，Fuzhou 350003，China）

The additional side force on force transducers is an important cause of the rotation effect of build-up systems.Different simulation models created to analyze the four dimension variables of the balance structure in a new build-up system based on Finite Element Method.The test results indicate that the fluctuation quantity of the additional side force decreases as the inertia moment，thickness and bearing base height of a balance platen within a certain range，whereas the smallest fluctuation quantity of the additional side force can be obtained when the elastic modulus of the balance platen is around 150GPa.The additional side force therefore can be restrained by a specific balance structure.

build-up system；rotation effect；FEM；balance structure；additional side force

A

1674-5124（2015）09-0110-05

2015-01-07；

2015-02-20

国家科技部重大科学仪器专项（2011YQ090009）

韦铁平（1984-），男，广西贵港市人，博士，专业方向为强度设计和力值计量研究。