时域中核信号正反相放大滤波电路数字模型仿真分析

周　靖，周建斌，马英杰，王　敏，赵祥，喻　杰，郝　宽

时域中核信号正反相放大滤波电路数字模型仿真分析

周靖，周建斌，马英杰，王敏，赵祥，喻杰，郝宽

（成都理工大学核技术与自动化工程学院，四川成都610059）

为实现在时域中对核信号前置放大滤波电路进行数字分析，以常用的正相和反相放大滤波电路为研究对象，阐述一种建立放大滤波电路数字模型的方法。通过推导电路的微分方程，并采用微分方程数值解的方法，将求解微分方程解析解转换为求解微分方程数值递推解，从而建立电路的数字模型。通过对这两种电路的数字模型进行仿真，达到对正相和反相放大滤波电路进行数字分析的目的。通过将数字模型应用于实时核脉冲信号分析，为进一步采用FPGA技术将放大滤波电路进行数字硬件实现提供必要的理论基础。

核脉冲信号；放大滤波电路；数字模型；时域数字分析；数字滤波

doi：10.11857/j.issn.1674-5124.2015.09.023

0　引言

核电子学中，反相放大滤波电路以及同相放大滤波电路［1］常被用作前置放大滤波电路，用于核脉冲信号的滤波、放大以及成形等。针对这类电路的分析方法有：1）推导出电路的微分方程，然后采用时域分析法或复频域分析法（s域分析方法）进行求解以得到方程解析解［2-4］，但求解过程往往很繁琐，不适用于信号的实时分析；2）通过拉普拉斯变换［5］，从时域转换到频域，但这种方法更多的是研究电路的频域特性，往往体现不出核脉冲信号在时域的一些特点，如脉冲宽度、脉冲形状等［6-7］；3）借助仿真软件进行电路模拟仿真，以达到确定相关参数等目的［8］；但仿真软件隐藏了工作过程，所以对电路的工作原理无从了解，并且需要模拟复杂的输入信号，存在一定的难度。

基于上述原因，本文从反相放大滤波电路以及同相放大滤波电路的微分方程出发，采用微分方程数值解的方法［9］，得到微分方程的数值递推解，从而建立这两种电路的数字模型。并且，数字模型的结构与输入信号无关，通过对数字模型进行仿真，则能对电路进行定量的数字分析。通过使用FPGA技术将数字模型进行硬件实现，则能对信号进行实时分析。

1　反相放大滤波电路

1.1数字模型

图1所示的反相放大滤波电路，具有非常广泛的应用，在核电子学中常作为前置放大电路。

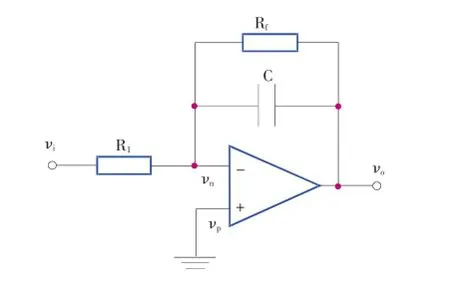
图1　反相放大滤波电路

对该电路进行分析，由基尔霍夫电流定律（KCL）可得：

由于核信号具有统计涨落的特点，式（3）将不可能有解析解。所以这里采用微分方程数值解的方法，将输入、输出的模拟信号分别转换成具有一定时间间隔的离散序列，即令νi=x［n］，νo=y［n］，d t=Δt，其中，Δt为时间间隔。则式（3）可表示为

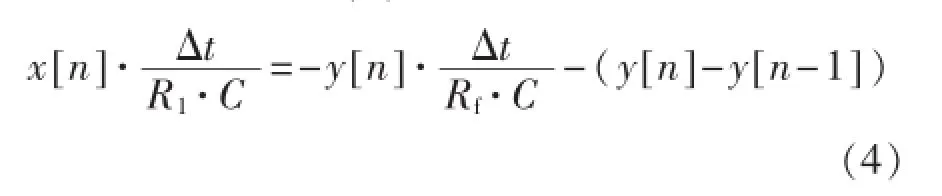
令k1=Δt/（CR1），k2=Δt/（CRf），则式（4）可表示为

式（5）为式（3）的数字递推解，同时也是图1所示电路的数字模型。

1.2仿真分析

以负指数信号表示核信号，在输入不同的负指数信号时，对负指数信号及反相放大滤波电路数字模型进行仿真。仿真中的核信号为

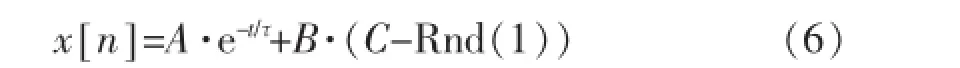
式中：A——标准负指数信号的幅度；

τ——时间常数；

B（C-Rnd（1））——噪声。

分别仿真4个信号作为输入信号，如下式所示：

式中i为整数。

仿真时，取Δt=50ns，图2是不同输入信号以及不同参数下的仿真波形图。其中，反相输出1（k1=0.5，k2=0.5）为R1=100Ω，Rf=100Ω和C=1nf时的等效输出信号；反相输出2（k1=0.01，k2=0.01）为R1=5 kΩ，Rf=5 kΩ和C=1 nf时的等效输出信号；反相输出3 （k1=0.01，k2=0.005）为R1=5kΩ，Rf=10kΩ和C=1nf时的等效输出信号。

图2中，输入脉冲的宽度由采样点数和Δt决定，由式（7）可以得到，输入信号Signal1的脉冲宽度为34.95μs，Signal2的脉冲宽度为50.45μs，Signal3的脉冲宽度为44.95μs。输出脉冲的宽度和形状随k1和k2的变化而变化，当Δt被确定后，通过调整电阻值R1、Rf和电容值C，可得到不同的k1和k2，从而得到不同的输出脉冲。

图1所示电路中，反馈电容C起到滤波作用，提高信噪比，与反馈电容并联的电阻Rf起泄放电容上电荷的作用。根据图2所示的仿真结果，若k2太大，滤波效果不明显，如反相输出1所示，此时输出信号的宽度近似和输入脉冲相等；若k2太小，放电时间常数C·Rf会很大，又起不到完全泄放电容上电荷的作用，会引起脉冲堆积，如反相输出3所示，脉冲实际宽度大于输入脉冲的宽度；反相输出2所示参数不仅达到了滤波效果，而且输出信号宽度近似和输入信号相等。上述3个输出信号的达峰时间都有所增加，但峰值都被减小。不同参数下输出信号的达峰时间、放大倍数分别如表1、表2所示。

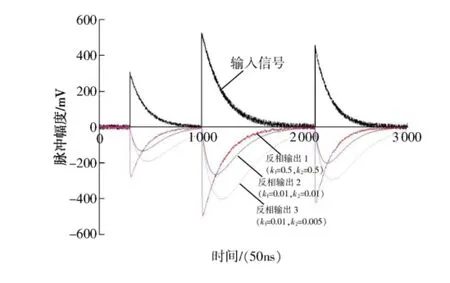
图2　反相放大滤波电路数字仿真

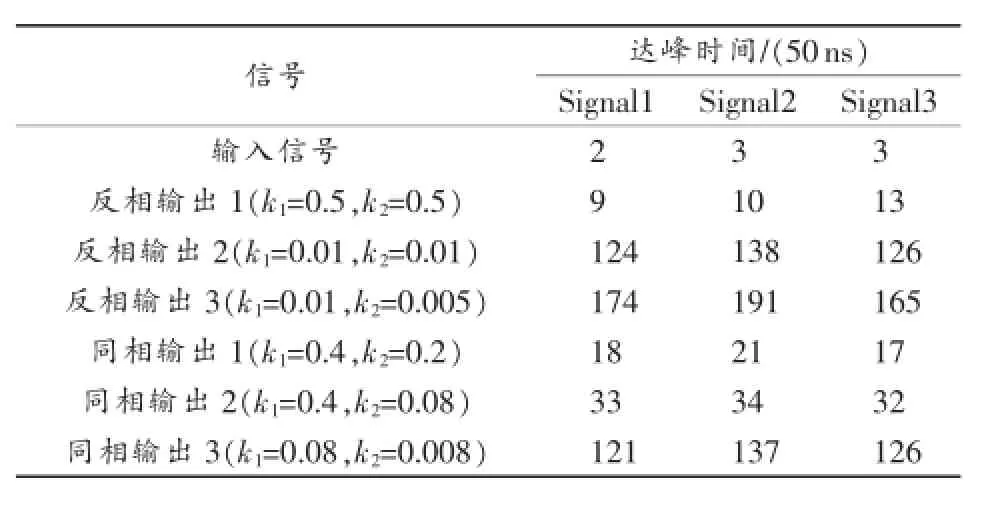
表1　不同参数下输出信号的达峰时间

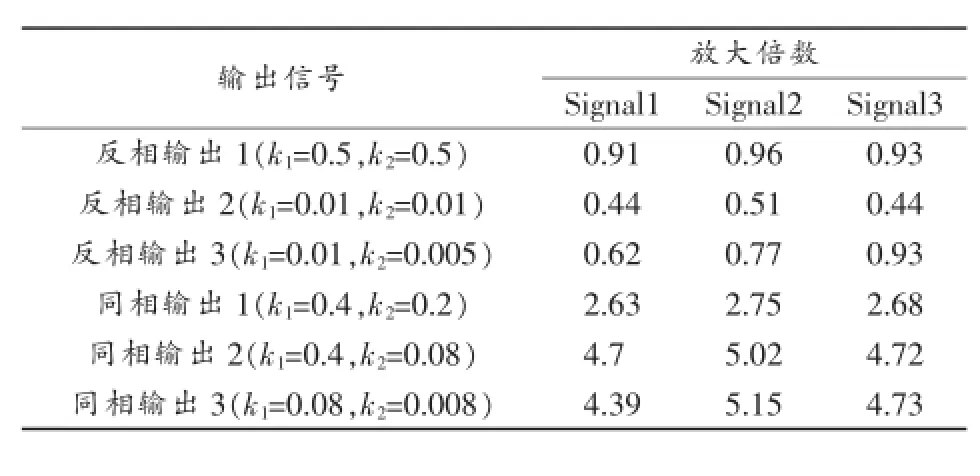
表2　不同参数下输出信号的放大倍数

2　同相放大滤波电路

2.1数字模型

图3为一个典型的带滤波功能的同相放大器。

对该电路进行分析，由KCL可得：

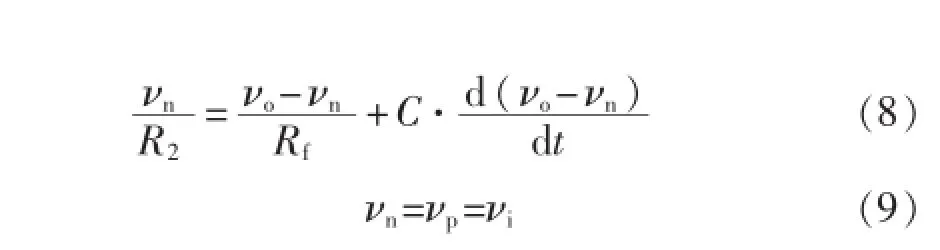
由式（8）、式（9）可得微分方程：

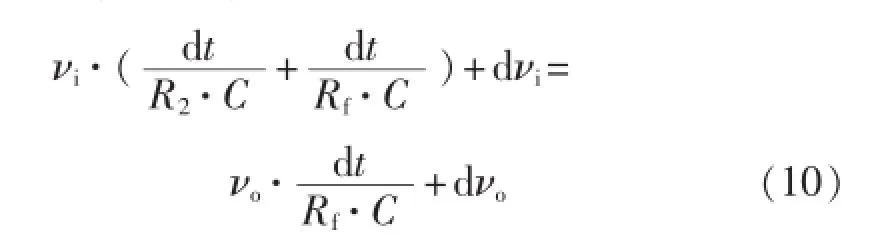
根据前面介绍的方法，式（10）可用数值递推解等价表示为

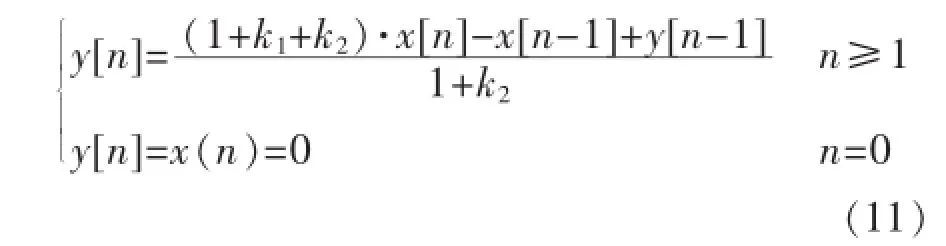
其中，k1=Δt/（C·R2），k2=Δt/（C·Rf）。

2.2仿真分析

采用式（7）的输入信号，取Δt=50 ns，对式（11）表示的数字递推模型进行仿真，结果如图4所示。其中同相输出1（k1=0.4，k2=0.2）为R2=125Ω，Rf=250Ω 和C=1 nf时的等效输出信号；同相输出2（k1=0.4，k2=0.08）为R2=125Ω，Rf=625Ω和C=1nf时的等效输出信号；同相输出3（k1=0.08，k2=0.008）为R2=625Ω，Rf=6.25kΩ和C=1nf时的等效输出信号。

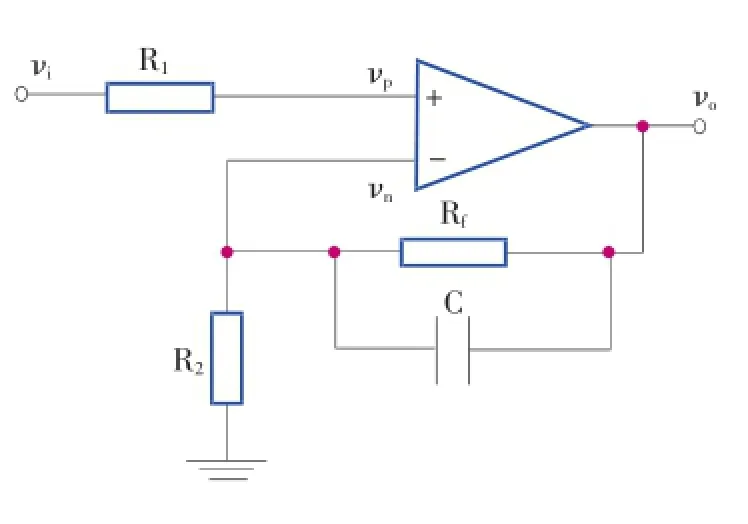
图3　同相放大滤波电路

由仿真结果可知，图3所示电路要实现更好的滤波效果，需要增大k1，同时减小k2。但若k2太小，会使得时间常数C·Rf很大，如同相输出3所示，虽然滤波效果有所提高，但电容上电荷不能完全被泄放；并且若k1太大，k2太小，输出信号将被放大很多倍，有可能使信号失真。同相输出1和同相输出2的输出脉冲宽度近似等于输入脉冲，同相输出3的输出信号的实际脉冲宽度大于输入信号。输出信号的达峰时间都有所增加，同时峰值都被放大。不同参数下输出信号的达峰时间、放大倍数分别如表1、表2所示。

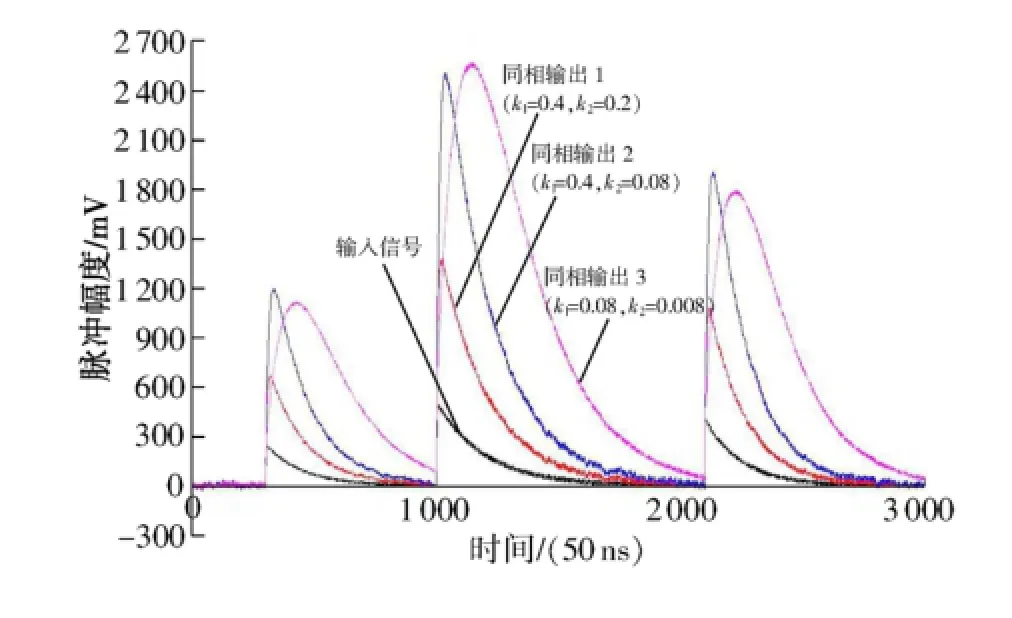
图4　同相放大滤波电路数字仿真

3　滤波效果的对比研究

将图2、图4中滤波结果进行局部放大（50～70μs），结果分别如图5、图6所示。

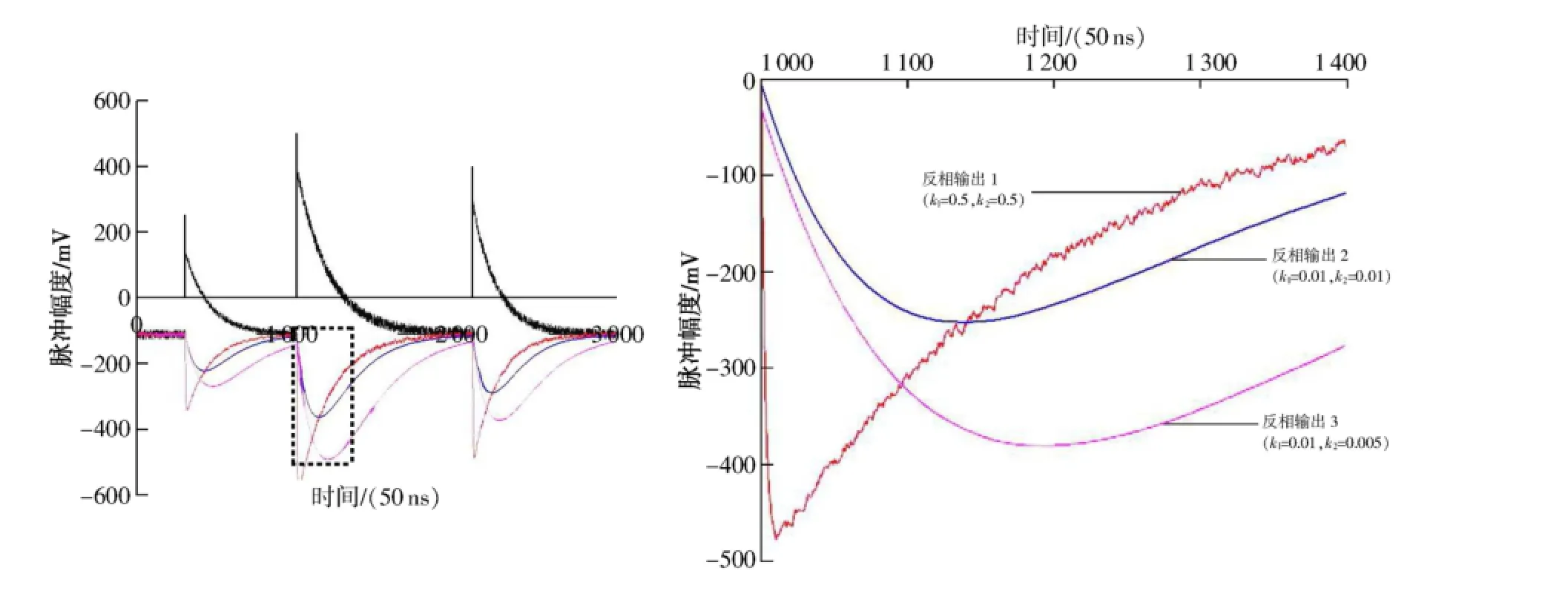
图5　反相放大滤波电路仿真结果局部放大

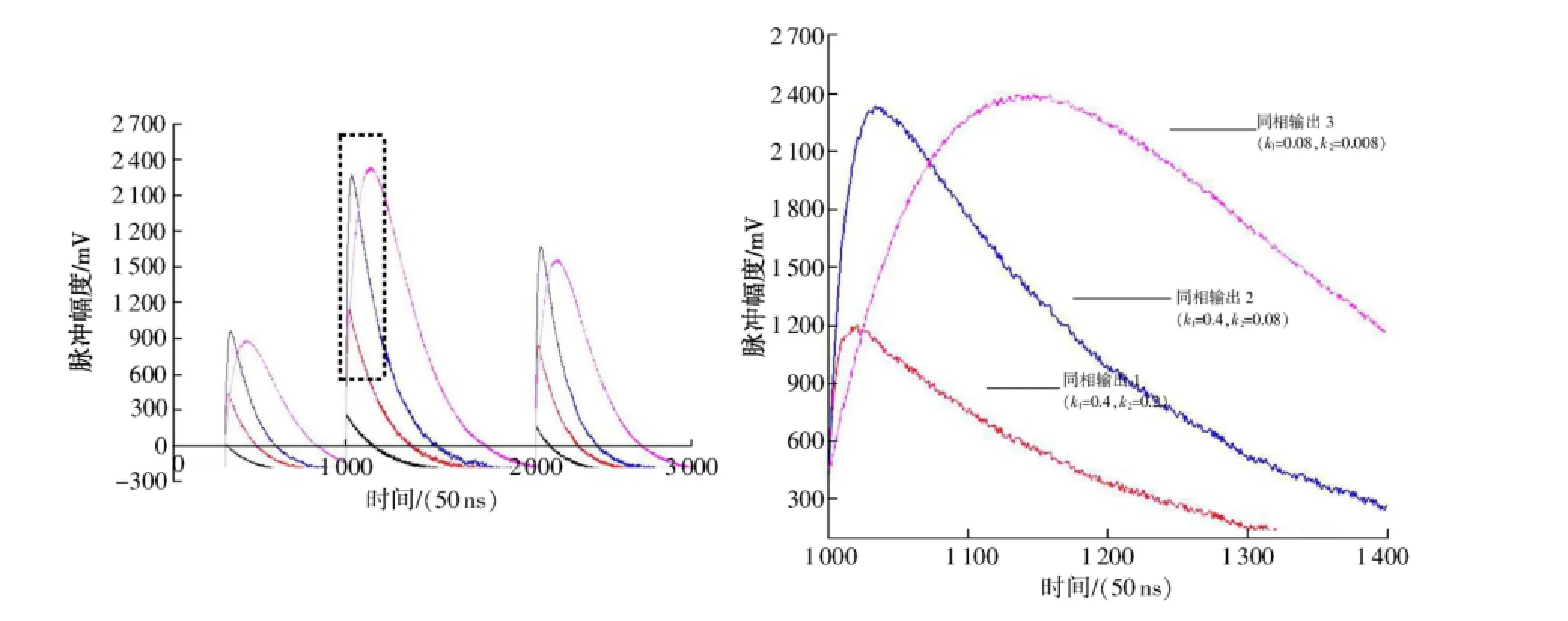
图6　同相放大滤波电路仿真结果局部放大

对比图5和图6可以看出，图6中的输出信号仍存在明显的噪声，峰值受噪声影响较大；而图5中的反相输出1和反相输出2基本平滑，峰值受噪声影响较小。不同参数下输出信号的信噪比（SNR）如表3所示（输入信号的信噪比为10dB）。

可以看出，反相放大滤波电路的滤波效果要好于同相放大滤波电路。当然，可在图6中继续增大同相输出3的k1，减小k2，以获得更好的滤波效果，但是这会导致输出信号有一个较长的延时，在高计数率情况下，输出信号将会发生严重堆积。

采用本文建立的放大滤波电路的数字模型对实测的核脉冲信号进行放大滤波处理，结果如图7所示。

综上所述，在核辐射测量的实际应用中，常常采用反相放大滤波电路作为核信号前置放大滤波电路。而对于同相放大滤波电路，一般在经过改进后组成S-K滤波器，用于对前级放大电路的输出信号进行放大和成形。

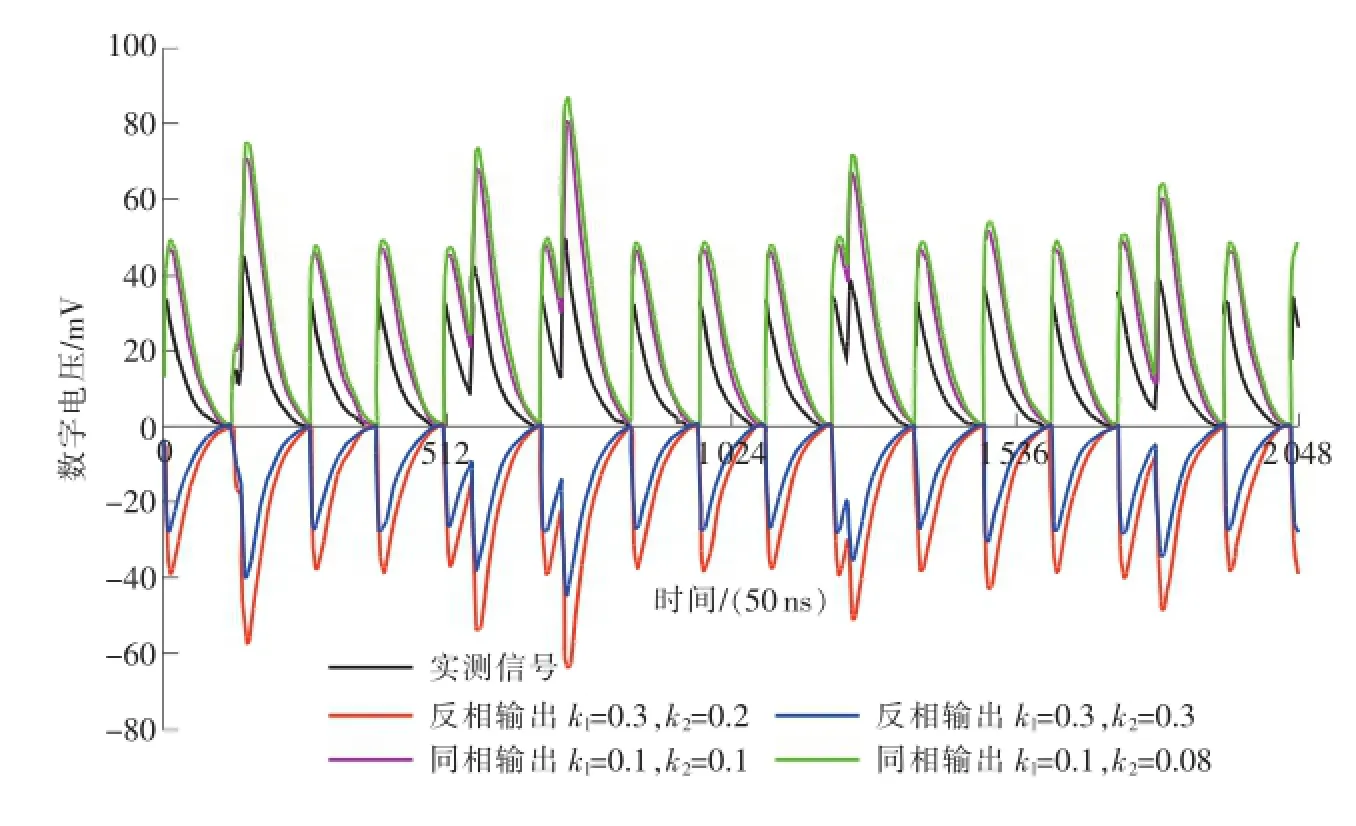
图7　实测信号的滤波效果

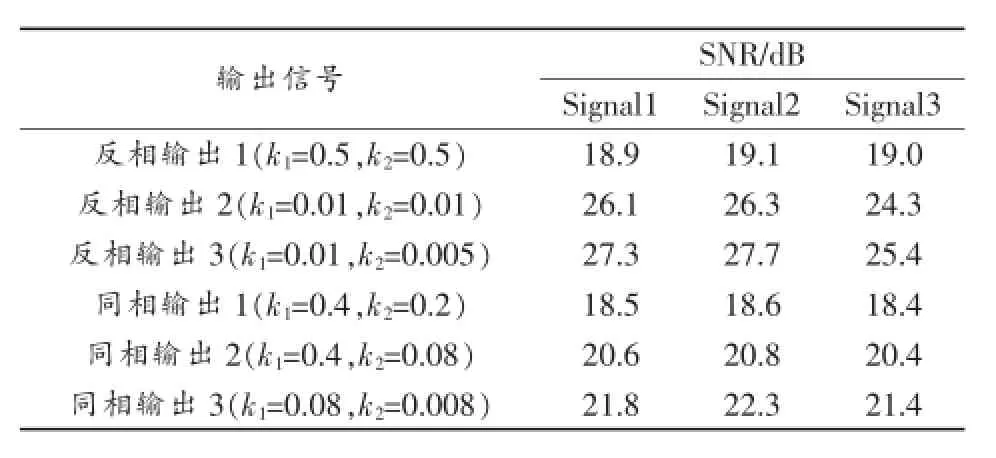
表3　不同参数下的信噪比

4　结束语

本文阐述了一种在时域内用数字化技术定量分析核信号放大滤波电路的方法，对核电子学中常用到的反相放大滤波电路和同相放大滤波电路进行了数字建模，并对输出信号的达峰时间、放大倍数以及SNR进行了仿真分析。对于核脉冲信号，反相放大滤波电路的滤波效果好于同相放大滤波电路，但同相放大滤波电路的放大倍数好于反相放大滤波电路。这种数字模型的建立方法对确定核脉冲信号放大滤波电路中的相关参数具有指导意义。根据研究成果，通过进一步采用FPGA技术将放大滤波电路数字模型进行硬件实现，为满足在实际工程中对核脉冲信号进行数字放大与滤波的技术要求提供了理论基础。另外，文中阐述的数字建模方法非常简单且易于实现，这对完善该类电路分析的理论和方法也有一定的促进作用。

［1］Donald A.Neamen microelectronics：circuit analysis and design［M］.New York：McGraw-Hill，2011：652-653.

［2］Boylestad R L.Introductory circuit analysis［M］.10th Edition.London：Prentice-Hall，2000.

［3］傅恩锡，杨四秧.电路分析简明教程［M］.2版.北京：高等教育出版社，2009：130-208.

［4］James W N，Susan A R.电路［M］.周玉坤，冼立勤，译.北京：电子工业出版社，2011.

［5］何子述.信号与系统［M］.北京：高等教育出版社，2008：221-237.

［6］Zhou J B，Zhou W，Lei J R，et al.Study of timedomain digital pulse shaping algorithms for nuclear signals［J］.Nuclear Science and Techniques，2012（23）：150-155.

［7］Zhou J B，Zhou W，Hong X.Improvement of digital S-K filter and its application in nuclear signal processing［J］.Nuclear Science and Techniques，2013（24）：060401.

［8］颜强，洪兵，李桃生，等.便携式高能中子剂量仪的模拟电路系统设计［J］.核电子学与探测技术，2013，33（9）：1057-1061.

［9］Alan V O，Ronald W S.Discrete-time signal processing［M］. 2nd Edition.London：Prentice-Hall，1999.

Simulation analysis of numericalmodel of inverting and noninverting am p lifier filter circuit for nuclear signal in time domain

ZHOU Jing，ZHOU Jianbin，MA Yingjie，WANG Min，ZHAO Xiang，YU Jie，HAO Kuan
（College of Nuclear Technology and Automation Engineering，Chengdu University of Technology，Chengdu 610059，China）

A method of establishing a circuit numerical model has been proposed in this paper to analyze numerically nuclear signal preamplifier filter circuits in time domain based on inverting and noninverting amplifier filter circuits.The problem of how to solve specific analytical solutions for differential equations is converted to the problem of how to solve numerical recursive solutions by deriving the differential equations for circuit and by applying the numerical solution of differential equations.A numerical model for circuit is established accordingly.The numerical models of the two circuits mentioned above are analyzed numerically in time domain and their filtering characteristics re-recognized through simulation experiment.The numerical models are applied to analyze real-time nuclear pulse signals，and also provide a theoretical basis fort the implementation of amplified filter circuits in hardware through FPGA technology.

nuclear pulse signal；amplifier filter circuit；numericalmodel；numerical analysis in time domain；digital filtering

A

1674-5124（2015）09-0101-05

2015-02-07；

2015-03-20

国家自然科学基金项目（11475036，41404108）

周靖（1990-），男，四川安岳县人，硕士研究生，专业方向为核仪器与测控技术。