未知风场扰动下无人机三维航迹跟踪鲁棒最优控制

张 坤高晓光

（西北工业大学电子信息学院 西安 710129）

未知风场扰动下无人机三维航迹跟踪鲁棒最优控制

张 坤*高晓光

（西北工业大学电子信息学院 西安 710129）

该文提出一种未知风场扰动下无人机精确3维航路跟踪的鲁棒最优控制律。该控制律基于跟踪虚拟目标的思想，将风场扰动加入无人机运动方程，采用反馈线性化将无人机的非线性动力学方程变换为线性状态方程。假设风场扰动已知的条件下，采用线性二次型调节器推导出能够跟踪3维航路的最优控制律。进一步考虑未知的风场扰动，设计鲁棒控制项代替最优控制律中的风场参数，得到能够抑制未知有界风场干扰的鲁棒最优控制律，并采用Lyapunov稳定性理论证明该闭环系统的全局渐近稳定性。仿真表明该控制律能够实现在未知风场扰动下无人机精确3维航迹跟踪，且具有良好的跟踪性能。

3维航迹跟踪；最优控制；鲁棒控制；风场扰动

1 引言

无人机由于具有良好的机动性和低成本高效能的特点，在侦察、预警、通信等军事领域，环境监测、地图测绘、灾难救援等民用领域得到了广泛的应用［1］。无人机在执行一些预定任务，如城区监控、灾难搜索和救援，需要在城市建筑之间飞行或者在复杂地形表面贴近飞行［2］，精确3维航迹跟踪能力是成功执行这些任务的关键。无人机执行这些任务时，外界风场干扰能够显著影响其航迹跟踪效果［2］。而且风场扰动变化复杂，存在定常风、切变风、随机风等多种扰动形式［3］。因此，研究无人机在风场扰动下精确3维航迹跟踪控制具有较大的挑战性和实际意义［4］。

国内外很多学者对外界扰动条件下精确跟踪控制问题进行了研究，目前研究方法主要分为两类：（1）设计干扰观测器［1，4-8］，基本思想是分析扰动的各种因素，建立扰动随时间和空间变化的模型，之后通过各种滤波算法结合采集到的量测数据进行扰动估计，使用估计扰动进行反馈控制；（2）设计鲁棒控制器［9-12］，基本思想是将扰动看作不确定因素，其统计特性未知，但其上界可以估计，通过设计具有良好鲁棒性能的控制器抑制扰动。

在风场扰动的建模估计方面，文献［6］提出了风场随时间和空间变化的 Markov自回归模型，在该模型的基础上，文献［5］基于部分观测Markov决策过程理论研究了无人机在风场干扰条件下跟踪地面目标的航路规划算法。文献［7，8］提出了使用无人机自身的机载传感器测量信息来估计风场及其变化的算法，并给出了估计误差分析。对风场扰动进行实时估计的方法需要无人机携带相应的传感器，且实时估计增加了无人机计算负载。

设计鲁棒控制器抑制风场干扰方面，目前大部分的研究关注2维平面内精确航路跟踪控制。文献［13］基于虚拟目标的方法，使用纯追踪导引律的基本思想推导出无人机能够跟踪2维平面航路的控制过载，仿真实验表明该方法在恒定风场扰动下与传统的线性反馈法设计的控制器相比具有更好的性能。文献［2，3］通过为规划航路构造向量场来产生控制指令，可以在恒定风场干扰下有效跟踪2维直线和圆弧航路，但对于复杂航路构造向量场存在困难。文献［14］提出一种将追踪导引和视线导引相结合的控制律，该控制律在恒定风场干扰下跟踪2维直线和圆弧的性能比文献［13］更好。上述文献均假设风场扰动为恒定风速和风向，而实际的风场扰动是时变的，而且其变化也不能精确估计。另外，上述文献的控制律仅适用于2维航路跟踪，没有涉及3维跟踪问题，而3维跟踪控制问题更复杂。在3维空间航路跟踪方面，贺跃帮等人［15］针对无人直升机的3维轨迹跟踪问题，提出了一种基于自适应动态面的控制方法；王怿等人［16］研究了固定翼无人机在动态环境中实时避障的3维路径跟踪算法。上述文献研究了3维空间航路跟踪控制，但没有考虑外界风场扰动的影响，在外界风场扰动下无法实现精确航迹跟踪。

研究扰动条件下控制器设计的工作也给我们的思路带来了一些启发。黄静等人［17］提出了针对含不确定性的旋转二体绳系卫星的姿态跟踪控制问题的鲁棒最优控制器。贾鹤鸣等人［18］研究了未知海流干扰作用下欠驱动无人水下航行器的3维航迹跟踪控制，采用迭代方法设计了非线性滑模控制器，实现了3维航迹的精确跟踪。文献［19］研究了未知高阶仿射非线性系统的轨迹跟踪问题，提出了基于线性化的鲁棒神经自适应协同控制方法。

本文在前人工作的基础上，针对未知风场扰动下无人机的精确3维航迹跟踪问题，设计了一种鲁棒最优控制律。首先假设风场干扰已知或者可以精确测量，将无人机非线性动力学方程线性化，使用线性二次型调节器推导出最优控制律。进一步考虑未知的风场扰动，采用滑模变结构控制［12］的基本思想设计鲁棒控制项代替最优控制律中的风场参数，得到能够抑制有界风场干扰的鲁棒最优控制律，并采用 Lyapunov稳定性理论证明该闭环系统的全局渐近稳定性。本研究在导引控制律设计中考虑未知风场扰动的影响，给出了3维航迹跟踪鲁棒最优控制律，该导引控制律在风场扰动条件下具有良好的跟踪性能。

本文后续结构安排如下：第2节给出了无人机动力学方程的线性化，并提出问题；第3节设计了该航迹跟踪问题的最优控制律；第4节考虑未知的风场扰动，设计了鲁棒最优控制律；第5节仿真验证该鲁棒控制律精确跟踪3维航迹的性能；最后是结论和讨论。

2 问题提出

针对无人机6自由度刚体动力学的12个状态方程［20］，采用非线性动态逆方法［21.22］，得到空速、航迹倾角和航

无人机在飞行过程中，受到风场的影响，故在无人机运动学方程中加入风场扰动。

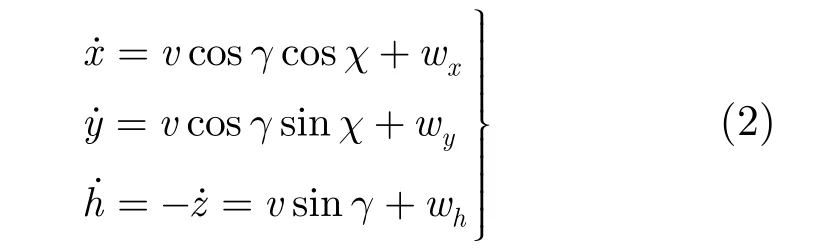
这里， x，y，z表示无人机在欧美坐标系中的3个坐标分量，h表示飞行高度， w=（wxwywh）分别表示未知风场扰动在参考坐标系各坐标轴上的分量，其大小随时间变化，变化率未知，其变化率记为w˙，w，w˙有界。

为便于处理无人机的非线性动力学方程，采用反馈线性化对非线性方程式（1）和式（2）进行变换。对无人机动力学方程，采用变换如式（3）所示：

这里，变换矩阵T为

经过变换之后，无人机方程变为

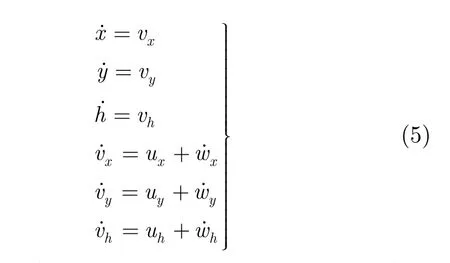
注意到上述变换是可逆的，所以只需对式（5）中的ux，uy，uh进行设计，之后再进行反变换即可得到所需的控制指令 vc，γc，χc。

为了使无人机按照规划航路飞行，假设有一个虚拟目标在规划航路上飞行，即该虚拟目标的飞行航迹是规划航路，无人机通过跟踪该虚拟目标实现精确跟踪航路。由于规划航路不受风场的影响，故虚拟目标的运动不受风场扰动的影响。假设规划航路光滑，各坐标分量的一、二阶导数都存在。令

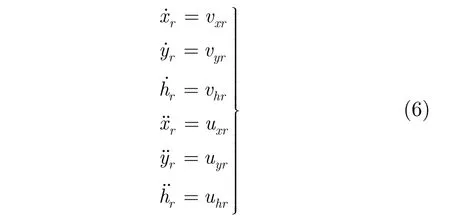
从而可以得到与无人机方程式（5）相似的虚拟目标的动力学方程。其中 xr，yr分别表示虚拟目标在欧美坐标系中的水平面内的坐标分量， hr表示高度。

我们的问题是对无人机设计反馈控制律使得在未知有界风场扰动和任意初始条件下有式（9）成立：

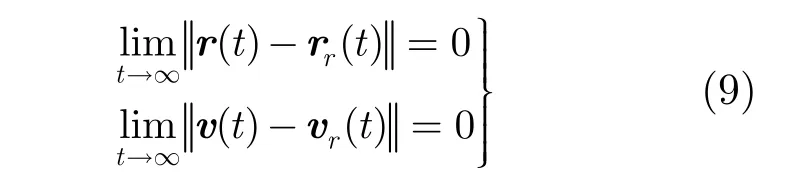
3 最优控制律设计

首先，假设风场扰动可以精确测量，即扰动变化已知，在该假设下设计最优控制律。

定理 1若风场变化已知，给定如式（8）表示的虚拟目标和式（7）表示的无人机动力学方程，按式给（10）出的控制量能够保证式（9）成立，即无人机飞行航迹渐进收敛于规划航路。其中，在证明过程中给出。

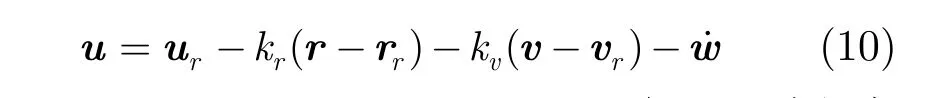
证明为简化推导，令则关于 ξ，η的状态方程为

设计线性二次型调节器LQR（Linear Quadratic Regulator） 使 x →0。性能指标为

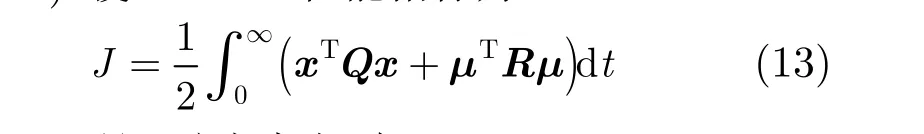
其中，Q，R是正定加权矩阵。

通过使性能指标最小化，可以得到反馈控制：

其中，反馈增益矩阵K为

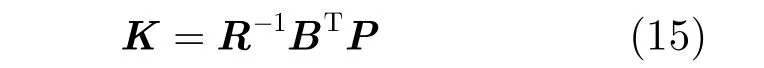
P为如下Riccati方程的解：

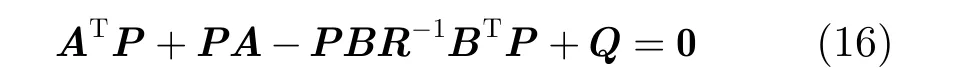
现在需要设计 Q，R并求解P。首先令R为单位阵，即

令加权矩阵Q的形式为

其中， q1，q2为设计参数且 q1＞ 0，q2＞ 0。

求解P之前需要考察LQR的解存在的两个条件是否满足：

这里 n= 6，经验证， A，B能控。

（2）Q，R是否为正定矩阵。显然，上面给出 Q，R的形式都为正定矩阵。

上述两个条件均满足，故LQR的解存在。

为求解P，将其分块，令

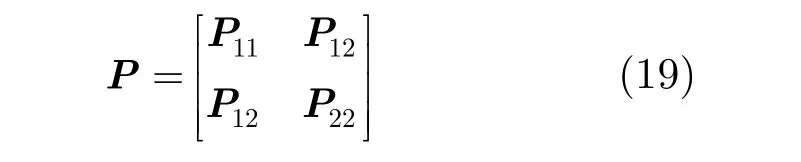
代入Riccati方程式（16）可得

由式（20）解得

将求得的P代入式（15），可得反馈增益矩阵为

故该LQR的反馈控制量为

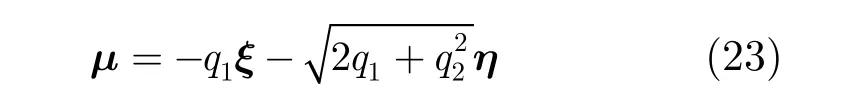
因此，无人机控制量u为

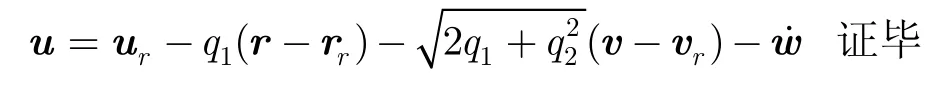
4 鲁棒最优控制律设计

事实上，风场扰动是未知的，而式（10）中包含风场扰动w˙，故式（10）给出的控制量无法实现。为此将式（10）中的扰动改为鲁棒项，希望设计一种鲁棒控制律。

将未知风场扰动替换为鲁棒项 uτ，得到鲁棒控制量为：

现在需要设计鲁棒项 uτ。

定理 2针对未知的风场扰动，给定如式（8）表示的虚拟目标和式（7）表示的无人机动力学方程，按式（25）给出的鲁棒项能够保证式（9）成立，即无人机飞行航迹渐进收敛于参考航路。

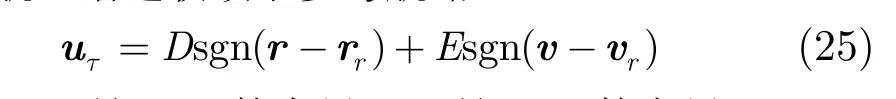
证明对系统式（11），取Lyapunov候选函数为

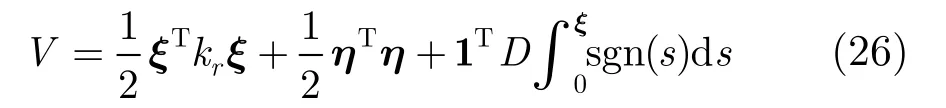
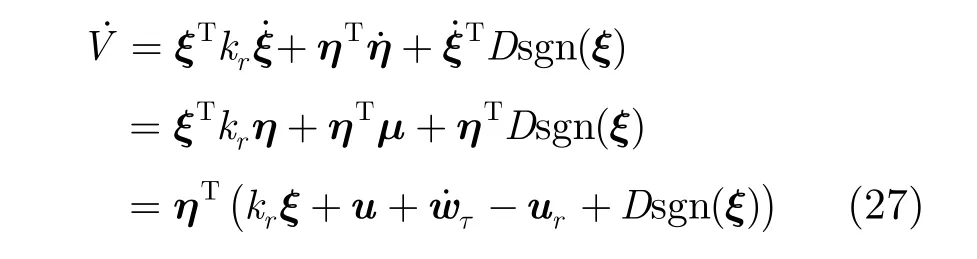
代入控制量式（24），式（25），得到

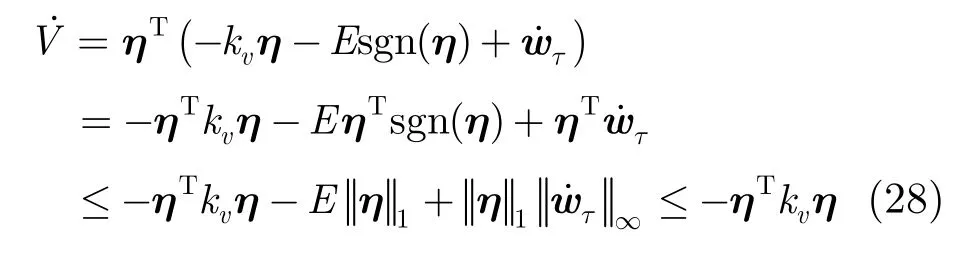
式（28）用到了Holder不等式，∀ a，b ∈ℝn， 1 ≤p≤∞， 1/ p + 1/ p= 1，那么

显然，x =0是系统式（11）的一个平衡点，式（26）给出的Lyapunov候选函数 V:ℝ6→ℝ是连续可微且径向无界的正定函数，由式（28）可知 ∀ x ∈ℝ6，有 V˙≤ 0。另外，在集合中除平凡解 x ≡0之外没有其他解。由LaShalle不变原理［23］可知，原点是全局渐近稳定的。 证毕

需要说明的是，由于符号函数的跳变，式（25）给出的鲁棒项 uτ会导致控制系统振颤［11］。为了降低振颤，采用饱和函数代替符号函数，鲁棒项改为

其中，饱和函数定义为

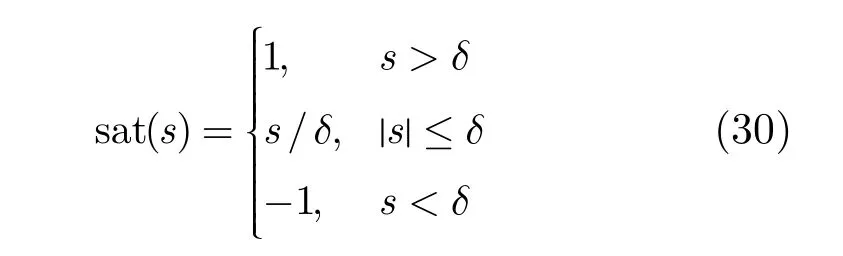
δ是确定滑模边界层的常数。

注：对于符号函数和饱和函数，一般定义为标量形式。若其自变量是向量，其结果是对向量中的元素逐个使用该函数得到的向量。

5 仿真实例

为验证提出的精确3维航路跟踪控制律的有效性，在风场干扰条件下，将控制律应用于无人机跟踪3维空间内上横8字形的跟踪。其中，仿真1验证第3节最优导引控制律在已知风场变化时的跟踪性能，仿真2验证第4节鲁棒最优控制律在未知有界风场干扰时的跟踪性能，仿真3与已有的研究［14］进行比较，验证本文提出的控制律跟踪性能更优。在仿真实验中，仿真时间为100 s，仿真步长为0.01 s，无人机性能参数无人机初始状态是r=（160， 10， 260） m， v = 13 m/s， γ= 0°， χ= 45°。上横8字形方程［24，25］为

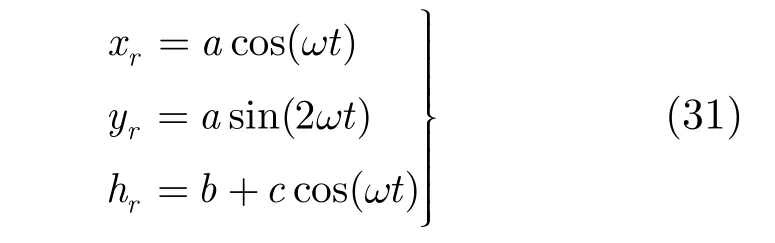
仿真中取a=150， b=150， c=100， ω=π /50。控制律中参数 q1= 1，q2= 1。

5.1 验证最优导引控制律

仿真1 在风场干扰已知或能精确测量条件下，验证最优导引控制律的跟踪性能。取风速随时间正弦变化，sin（πt /10）m/s， wh= sin（πt /10）m/s，如图1所示。在已知风场扰动条件下，无人机跟踪上横8字形的仿真结果如图2～图5所示。

图2显示无人机在已知风场扰动下飞行的3维航迹和参考航路，从图中可以看出，最优导引控制律能够使无人机的飞行航迹收敛到3维参考航路。图3显示无人机与虚拟目标的位置误差和速度误差随时间的变化曲线，从图中可以看出，位置误差超调量为0 m，位置误差收敛到稳态的时间是6 s，稳态位置误差为0 m。图4显示无人机与虚拟目标的速度误差随时间变化的曲线，从图中可以看出，速度误差有一定的超调量，速度误差收敛到稳态的时间是6 s，稳态速度误差为0 m/s。图5显示无人机的控制量，包括空速指令、航迹偏角和航迹倾角指令随时间变化的曲线。仿真说明最优导引控制律可以有效跟踪3维空间复杂曲线。

5.2 验证鲁棒最优导引控制律

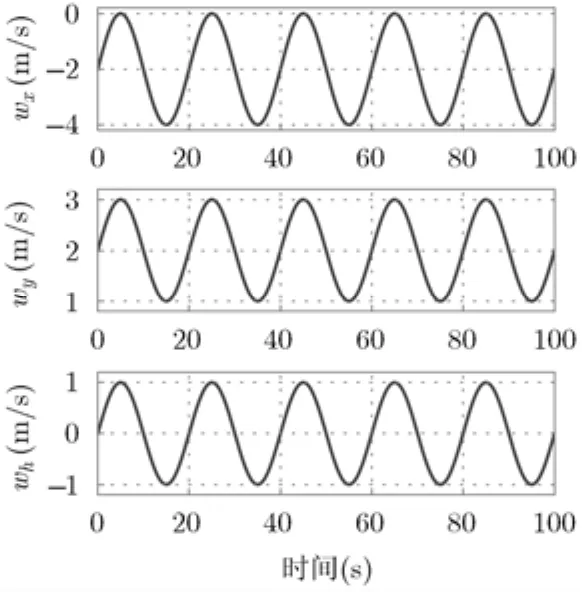
图1 仿真1的风场设置

图2 仿真1跟踪8字形的航迹和参考航路

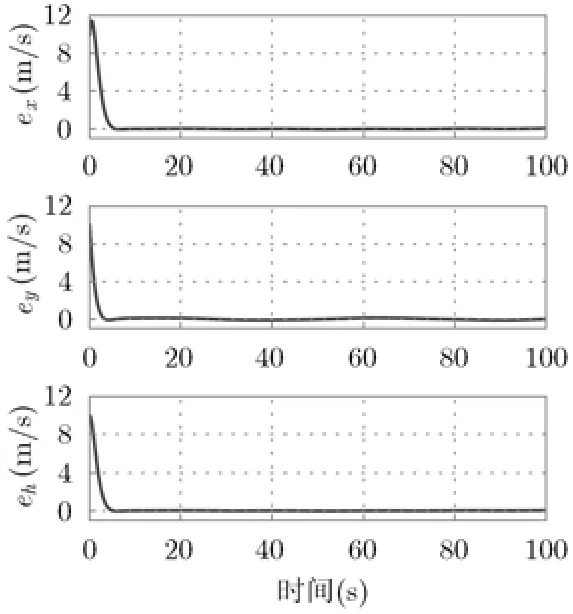
图3 仿真1跟踪8字形的位置误差

仿真2 在风场扰动未知的条件下，验证鲁棒最优导引控制律的跟踪性能。其中鲁棒项采用式（29），

饱和函数参数取 δ= 0.1。仿真中风场干扰设置按照文献［5，6］的方法，取风速3个分量为 w =（2，2，0）T+Ek，其中 Ek=（ekxekyekh）T，ekx，eky，ekh～ N（0，0.52），风速采样时间为1 s，采样时间内任意时刻的风速由插值得到。风场干扰如图6所示。取控制律中常数 D=5，E= 4。在未知风场扰动条件下，无人机跟踪上横8字形的仿真结果如图7～图10所示。

图4 仿真1跟踪8字形的速度误差

图5 仿真1跟踪8字形的控制指令

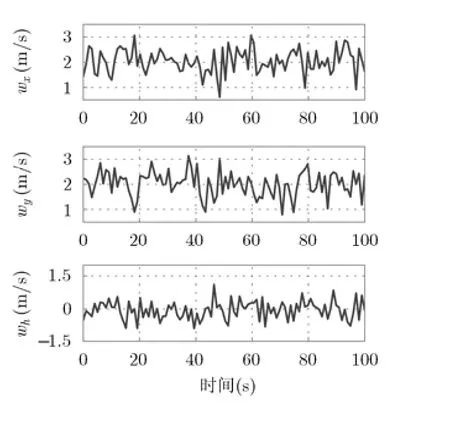
图6 仿真2的风场设置

图7显示无人机在未知风场扰动下飞行的3维航迹和参考航路，从图中可以看出，鲁棒最优导引控制律能够使无人机的飞行航迹收敛到3维参考航路。图8，图9显示无人机与虚拟目标的位置误差和速度误差随时间的变化曲线，从图中可以看出，与已知风场变化相比，位置和速度误差收敛到稳态的时间不变，稳态位置误差为0 m，稳态速度误差在0 m/s附近，说明鲁棒最优控制律可以有效抑制未知风场扰动。图10显示无人机的控制量，包括空速指令、航迹偏角和航迹倾角指令随时间变化的曲线。仿真说明鲁棒最优导引控制律可以在未知风场扰动下有效跟踪3维空间复杂曲线。

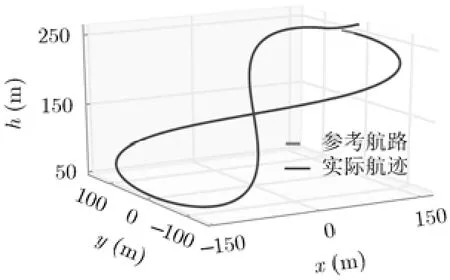
图7 仿真2跟踪8字形的航迹和参考航路

5.3 与现有导引律比较

为了说明本文提出的鲁棒最优控制律（Robust Optimal Guidance Law， ROGL）在未知风场干扰条件下具有更好的精确航迹跟踪性能，与现有的导引律（Pursuit-Line of Sight Guidance Law， PLSGL）［14］进行对比实验。由于PLSGL是在2维导引律，因此在对比实验中以跟踪3维空间内平行于x-y平面上的直线航路为例。实验中的3维风场干扰未知，与仿真2的设置相同。文献的导引律参数为 k1=15，k2= 1。仿真初始条件如下：无人机初始状态是r=（2，15，0） m， v=13 m/s，γ = 0°，χ = 45°。参考航路参数是 rr=（0，0，0） m，vr=（13cos（π/4），13sin（π/4），0）m/s。仿真结果如图11，图12所示。为了便于对比，图11显示本文的ROGL 3维跟踪航迹在x-y平面投影与PLSGL的2维跟踪航迹。

图11显示两种导引律均能在未知风场扰动下使无人机航迹收敛到2维直线航路。图12显示使用两种导引律的无人机的位置误差，可以看出，本文提出的导引律和文献［14］的导引律的位置误差收敛到零附近的时间分别是6 s和23 s，最大位置误差（真实航迹在参考直线航路左侧取正、右侧取负）分别是17.45 m和49.70 m。说明本文提出的导引律能使无人机航迹更快收敛到参考航路，而且其收敛过程中超调量更小。另外，达到稳态之后，本文提出的导引律能够使无人机跟踪静态误差收敛到0 m，而文献［14］的导引律使无人机跟踪静态误差在0 m附近抖动。仿真结果表明，本文提出的导引律具有更优的跟踪性能，使无人机在未知风场扰动下航迹跟踪的精度更高。

6 结论和讨论

图8 仿真2跟踪8字形的位置误差

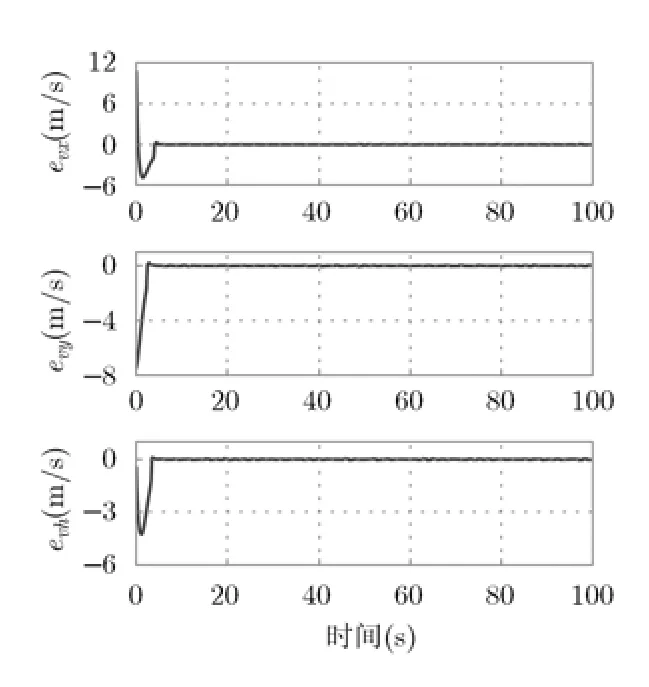
图9 仿真2跟踪8字形的速度误差

图10 仿真2跟踪8字形的控制指令

图11 跟踪直线的航迹比较

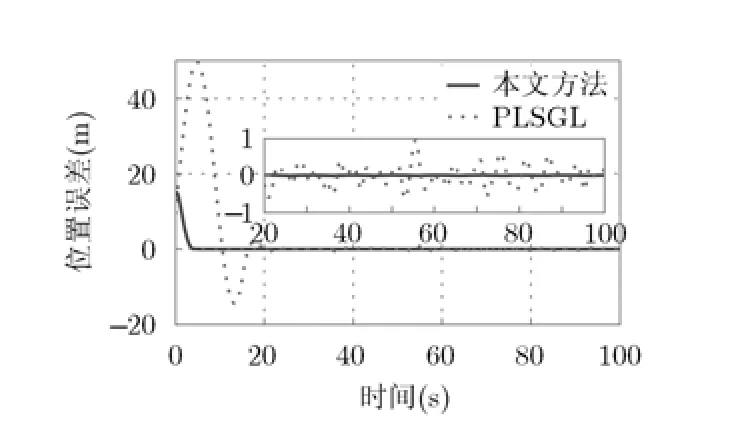
图12 跟踪直线的位置误差比较

本文讨论了未知风场扰动下无人机精确3维航路跟踪问题，提出了一种能够实现未知风场扰动下无人机精确3维航路跟踪的鲁棒最优导引控制律。将未知风场扰动引入到无人机运动方程中，采用反馈线性化将无人机的非线性动力学方程转化为线性状态方程。在风场能够精确测量的假设基础上，利用线性二次型调节器LQR推导出最优控制律。之后考虑未知的风场扰动，设计鲁棒控制项代替最优控制律中的未知风场参数，得到能够抑制有界风场干扰的鲁棒最优控制律，并采用 Lyapunov稳定性理论证明该闭环系统的全局渐近稳定性。采用饱和函数替代符号函数得到的鲁棒最优控制器，降低了符号函数跳变导致的系统振颤。本文提出的鲁棒最优控制律能够实现在已知或可精确测量的风场扰动下的无人机精确3维航迹跟踪的最优控制，实现在未知风场扰动下的无人机精确3维航迹跟踪的鲁棒最优控制，且在未知风场扰动下具有良好的跟踪性能。

进一步的工作可以从以下方面开展：（1）在鲁棒控制与对风场扰动实时估计相结合，设计性能更好的精确航迹跟踪控制器；（2）不仅考虑外界风场扰动的不确定性，还要考虑无人机动力学特性的不确定性，研究无人机动力学特性含有扰动项的精确航迹跟踪问题。

［1］ Cho A， Kim J， Lee S， et al.. Wind estimation and airspeed calibration using a UAV with a single-antenna GPS receiver and pitot tube［J］. IEEE Transactions on Aerospace and Electronic Systems， 2011， 47（1）: 109-117.

［2］ Nelson D R， Barber D B， Mclain T W， et al.. Vector field path following for miniature air vehicles［J］. IEEE Transactions on Robotics， 2007， 23（3）: 519-529.

［3］ 雷旭升， 陶冶. 小型无人飞行器风场扰动自适应控制方法［J］.航空学报， 2010， 31（6）: 1171-1176. Lei X S and Tao Y. Adaptive control for small unmanned aerial vehicle under wind disturbance［J］. Acta Aeronautica et Astronautica Sinica， 2010， 31（6）: 1171-1176.

［4］ Rysdyk R. Unmanned aerial vehicle path following for target observation in wind［J］. Journal of Guidance， Control， and Dynamics， 2006， 29（5）: 1092-1100.

［5］ Ragi S and Edwin C. UAV path planning in a dynamic environment via partially observable markov decision process［J］. IEEE Transactions on Aerospace and Electronic Systems，2013， 49（4）: 2397-2412.

［6］ Ailliot P， Monbet V， and Prevosto M. An autoregressive model with time-varying coefficients for wind fields［J］. Environmetrics， 2006， 17（2）: 107-117.

［7］ Langelaan J W， Alley N， and Neidhoefer J. Wind field estimation for small unmanned aerial vehicles［J］. Journal of Guidance， Control， and Dynamics， 2011， 34（4）: 1016-1030.

［8］ De Jong P M A， Laan J J， Veld A C， et al.. Wind-profile estimation using airborne sensors［J］. Journal of Aircraft，2014， 51（6）: 1852-1863.

［9］ Mcgee T G and Hedrick J K. Path planning and control for multiple point surveillance by an unmanned aircraft in wind［C］. 2006 American Control Conference， Minneapolis，MN， United States， 2006: 4261-4266.

［10］ Celentano L. Robust tracking method for uncertain MIMO systems of realistic trajectories［J］. Journal of the Franklin Institute， 2013， 350（3）: 437-451.

［11］ Ouyang P R， Acob J， and Pano V. PD with sliding mode control for trajectory tracking of robotic system［J］. Robotics and Computer-Integrated Manufacturing， 2014， 30（2）: 189-200.

［12］ Sabanovic A. Variable structure systems with sliding modes in motion control-a survey［J］. IEEE Transactions on Industrial Informatics， 2011， 7（2）: 212-223.

［13］ Park S， Deyst J， and How J P. Performance and lyapunov stability of a nonlinear path following guidance method［J］. Journal of Guidance， Control， and Dynamics， 2007， 30（6）: 1718-1728.

［14］ Kothari M， Postlethwaite I， and Gu D W. UAV path following in windy urban environments［J］. Journal of Intelligent & Robotic Systems， 2014， 74（3-4）: 1013-1028.

［15］ 贺跃帮， 裴海龙， 叶祥， 等. 无人直升机的自适应动态面轨迹跟踪控制［J］. 华南理工大学学报（自然科学版）， 2013， 41（5）: 1-8. He Y B， Pei H L， Ye X， et al.. Trajectory tracking control of unmanned helicopters by using adaptivedynamic surface approach［J］. Journal of South China University of Technology （Natural Science Edition）， 2013， 41（5）: 1-8.

［16］ 王怿， 祝小平， 周洲， 等. 3维动态环境下的无人机路径跟踪算法［J］. 机器人， 2014， 36（1）: 83-91. Wang Y， Zhu X P， Zhou Z， et al.. UAV path following in 3-D dynamic environment［J］. ROBOT， 2014， 36（1）: 83-91.

［17］ 黄静， 刘刚， 马广富. 含不确定性的绳系卫星姿态的鲁棒最优控制［J］. 宇航学报， 2012， 33（10）: 1423-1431. Huang J， Liu G， and Ma G F. Nonlinear robust optimal attitude tracking of tethered satellite system with uncertainties［J］. Journal of Astronautics， 2012， 33（10）: 1423-1431.

［18］ 贾鹤鸣， 张利军， 程相勤， 等. 基于非线性迭代滑模的欠驱动UUV 三维航迹跟踪控制［J］. 自动化学报， 2012， 38（2）: 308-314. Jia H M， Zhang L J， Cheng X Q， et al.. Three-dimensional path following control for an underactuated UUV based on nonlinear iterative sliding mode［J］. Acta Automatica Sinica，2012， 38（2）: 308-314.

［19］ El-Ferik S， Qureshi A， and Lewis F L. Neuro-adaptive cooperative tracking control of unknown higher-order affine nonlinear systems［J］. Automatica， 2014， 50（3）: 798-808.

［20］ Bugajski D J and Enns D F. Nonlinear control law with application to high angle-of-attack flight［J］. Journal of Guidance， Control， and Dynamics， 1992， 15（3）: 761-767.

［21］ 陈晓岑， 周东华， 陈茂银. 基于逆系统方法的DGMSCMG框架伺服系统解耦控制研究［J］. 自动化学报， 2013， 39（5）: 502-509. Chen X C， Zhou D H， and Chen M Y. Decoupling control of the gimbal servo system of the DGMSCMG based on the dynamic inverse system method［J］. Acta Automatica Sinica，2013， 39（5）: 502-509.

［22］ Snell S A， Nns D F， and Arrard W L. Nonlinear inversion flight control for a supermaneuverable aircraft［J］. Journal of Guidance， Control， and Dynamics， 1992， 15（4）: 976-984.

［23］ Khalil H K. Nonlinear Systems［M］. Upper Saddle River: Prentice Hall， 2002: 126-132.

［24］ Park S. Autonomous aerobatics on commanded path［J］. Aerospace Science and Technology， 2012， 22（1）: 64-74.

［25］ Cabecinhas D， Cunha R， and Silvestre C. A nonlinear quadrotor trajectory tracking controller with disturbance rejection［J］. Control Engineering Practice， 2014， 26: 1-10.

张 坤： 男，1985年生，博士生，研究方向为无人机导航制导与控制.

高晓光： 女，1957年生，教授，博士生导师，研究方向为航空火力控制与作战效能分析.

Robust Optimal Control for Unmanned Aerial Vehicles’Three-dimensional Trajectory Tracking in Wind Disturbance

Zhang Kun Gao Xiao-guang
（School of Electronics and Information， Northwestern Polytechnical University， Xi’an 710129， China）

This paper presents a robust optimal guidance control law for precise three-dimensional （3D） trajectory tracking of an Unmanned Aerial Vehicle （UAV） in wind disturbance. The wind disturbance is considered in the UAV’s kinematic model. The reference path is considered as a trajectory of a virtual target. Feedback linearization is used to transform the nonlinear dynamics of the UAV to linear state equations. Based on the assumption that the wind disturbance can be known precisely， an optimal control law is derived for the UAV's 3D trajectory tracking using the LQR （Linear Quadratic Regulator）. Then considering the unknown wind disturbance， a robust term is designed to replace the unknown wind disturbance， and a robust optimal control law is obtained. Global asymptotic stability of the closed-loop system is proved by Lyapunov stability theory. Simulations show that the proposed control law can achieve precise 3D UAV trajectory tracking with wind disturbance attenuation， and has good tracking performance.

3D trajectory tracking； Optimal control； Robust control； Winds disturbance

s: The National Natural Science Foundation of

TN966； V249

A

1009-5896（2015）12-3009-07

10.11999/JEIT150047

2015-01-07；改回日期：2015-08-02；网络出版：2015-10-13

*通信作者：张坤 zhangkunhn@mail.nwpu.edu.cn

国家自然科学基金（60774064）和教育部博士点基金（20116102110026）

China （60774064）； The Doctoral Fund of Ministy of Education of China （20116102110026）