基于杂波的收发分置MIMO雷达阵列位置误差联合校正方法

刘 源纠 博*刘宏伟夏香根（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）（美国特拉华大学电子与计算机工程学院 纽华克 19716）

基于杂波的收发分置MIMO雷达阵列位置误差联合校正方法

刘 源①纠 博*①刘宏伟①夏香根①②
①（西安电子科技大学雷达信号处理国家重点实验室 西安 710071）②（美国特拉华大学电子与计算机工程学院 纽华克 19716）

针对收发分置多输入多输出（MIMO）雷达发射端和接收端均存在位置误差的问题，该文提出一种基于杂波回波的收发阵列位置误差联合校正方法。该方法以最小化杂波回波数据的重构均方误差为准则，在杂波散射系数l1范数稀疏约束下，利用双迭代与凸优化方法对杂波散射系数和阵列位置误差参数进行联合优化求解，最终完成了对收发阵列位置误差的同时估计与校正。仿真实验表明了所提算法的有效性。

MIMO雷达；位置误差；参数估计；稀疏重构

1 引言

近年来，多输入多输出（Multiple Input Multiple Output， MIMO）雷达作为一种新体制雷达受到了广泛的关注［1-10］。相比于传统的相控阵雷达，MIMO雷达具有更高的系统自由度，它可以获得更好的角度估计性能［1-3］，以及灵活的进行发射方向图设计［4］。然而在实际应用中由于阵列误差不可避免，误差的存在将导致测角高分辨技术的性能严重下降［7］，使得发射方向图发生畸变［8］。因此，需要对阵列误差进行校正。

现有阵列误差校正方法可以分为有源校正方法［11，12］和自校正方法［13-16］两大类。有源校正是在空间设置方位已知的辅助信源对阵列误差参数进行离线估计，这类方法运算量小、实现简单。但是当辅助信源存在误差时，这类校正方法性能下降。自校正方法通常利用某种优化函数对空间信源方位与阵列扰动参数进行联合估计。现有的误差校正方法大多是将空间离散辐射源作为校正源，用来实现对接收阵列误差的校正。但由于阵列所接收到的数据与发射端误差无关，故此类方法不能校正发射阵列的误差。此外，这些方法对外置辐射源的数量以及辐射信号能量具有一定的要求，需要较高的应用条件，从而影响了校正方法的适用性。如果将杂波散射点作为校正源，利用经其反射的回波信号，便可实现对收发阵列误差的联合校正。并且由于杂波散射点普遍存在，因此基于杂波的误差校正方法不需要特殊的辐射源，更适合于一般的校正环境。基于此，文献［16］提出了一种基于杂波的阵列位置误差自校正算法，该算法以线性约束最小方差（LCMV）为准则，通过求解所有观测方向上的误差校正权，最终实现了对阵列误差的校正。但是，该算法没有考虑发射端阵列误差，与实际情况不符。其次，文献［16］中算法并没有估计出阵列位置误差的数值，对于不同的杂波场景而言，其获取的校正权矢量是不相同的，即该算法得到的校正权与杂波场景有关，若场景发生改变，则需要重新求取校正权矢量来完成阵列误差校正，这也限制了该算法在实际中的应用。

针对上述问题，本文在发射和接收端均存在阵列位置误差的情况下，提出了一种基于杂波的阵列位置误差联合校正算法。算法利用稀疏重构法与最速下降法交替迭代估计的方法，通过引入包含位置误差信息的补偿矩阵，对完备基矩阵进行逐步修正，利用修正后的基矩阵完成对杂波散射点方位角度及散射系数的估计，并由此得到收发阵列位置误差参数。该算法无需特殊的外置辐射源，可以同时完成对阵列收发端位置误差的校正。文中最后对算法进行了仿真验证。

2 MIMO雷达信号模型

考虑一收发分置MIMO雷达系统由 x-y平面内的M个发射天线和N个接收天线构成，收发阵列都为半波间距的均匀线阵（ULA）。假设发射阵列和接收阵列相距较近，则对于远场目标，可认为其波达方向（Direction Of Arrival， DOA）与波离方向（Direction Of Departure， DOD）近似相同，如图1所示。各发射天线发射正交波形，快拍数为 L。令第m个发射天线在第l时刻发射信号为 sml。那么阵列发射信号矩阵可以表示为

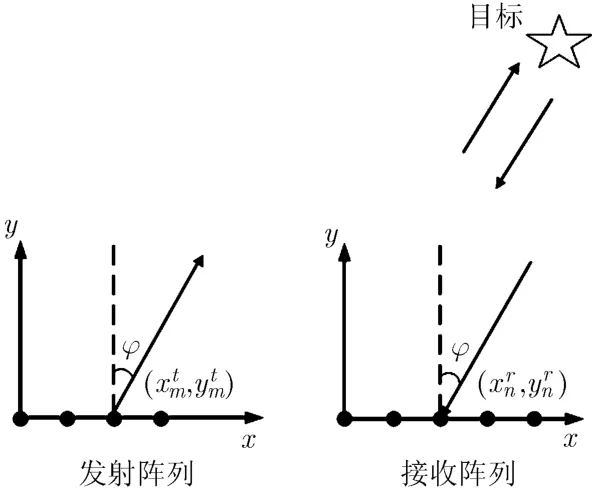
图1 收发分置MIMO雷达示意图

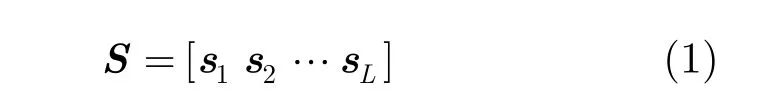
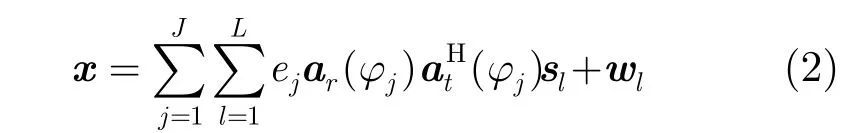
其中， ej为第j个杂波块的复散射系数，为噪声矢量，分别表示阵列在 φj方向上的发射导向矢量和接收导向矢量。记发射阵列中第m个阵元与接收阵列中第n个阵元的坐标分别为，则 at（ φj）和 ar（φj）可以由式（3）表示为

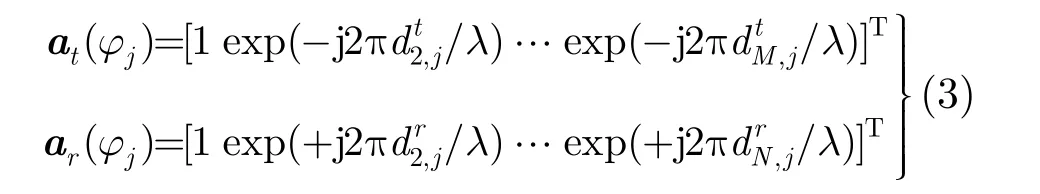
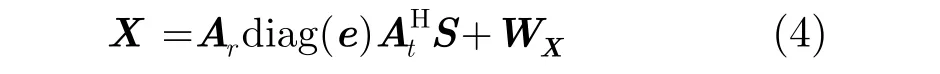
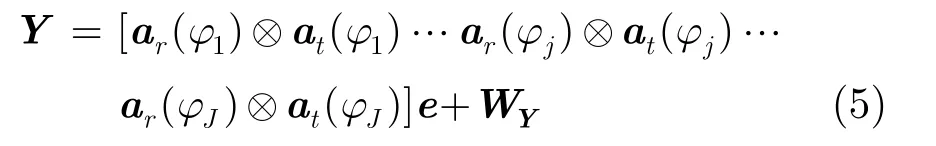
其中，⊗表示Kronecker积，WY∈CMN×1为噪声矢量。

在实际工程应用中阵列误差在所难免，这将导致实际的阵列流型相比理想的阵列流型出现一定的偏差。不失一般性，阵列误差一般包含幅相误差、位置误差和互耦误差，本文中假设收发阵列仅存在阵元位置误差。设发射阵列中第m个阵元与接收阵列中第n个阵元的位置误差分别记为和那么在存在阵列位置误差时阵列接收到的数据经过匹配滤波后的输出为

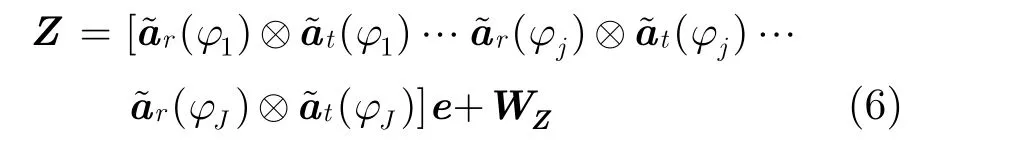
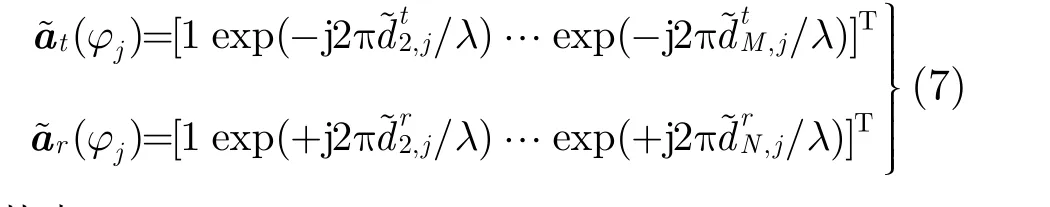
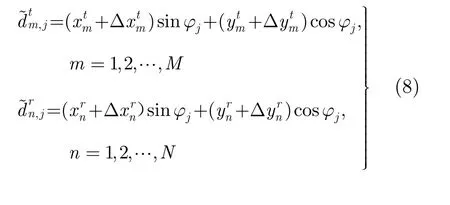
3 联合迭代自校正算法

由上一节的信号模型可知，经过匹配滤波后的回波数据Z中包含了杂波散射点的散射系数信息以及收发阵列的位置误差参数信息。本文的思想是将空间离散的杂波散射点作为观测校正源，从杂波回波数据Z中估计出收发阵列的位置误差。不失一般性，我们假设观测场景内某一距离单元的强杂波点是稀疏的（即散射系数矢量e中只有少量元素的模值较大，其余元素的模值都相对较小）。为此，本文提出了基于杂波的收发阵列位置误差联合校正算法，算法简要流程图如图2所示，下面对图2中的具体操作步骤进行说明。

3.1 杂波散射系数估计

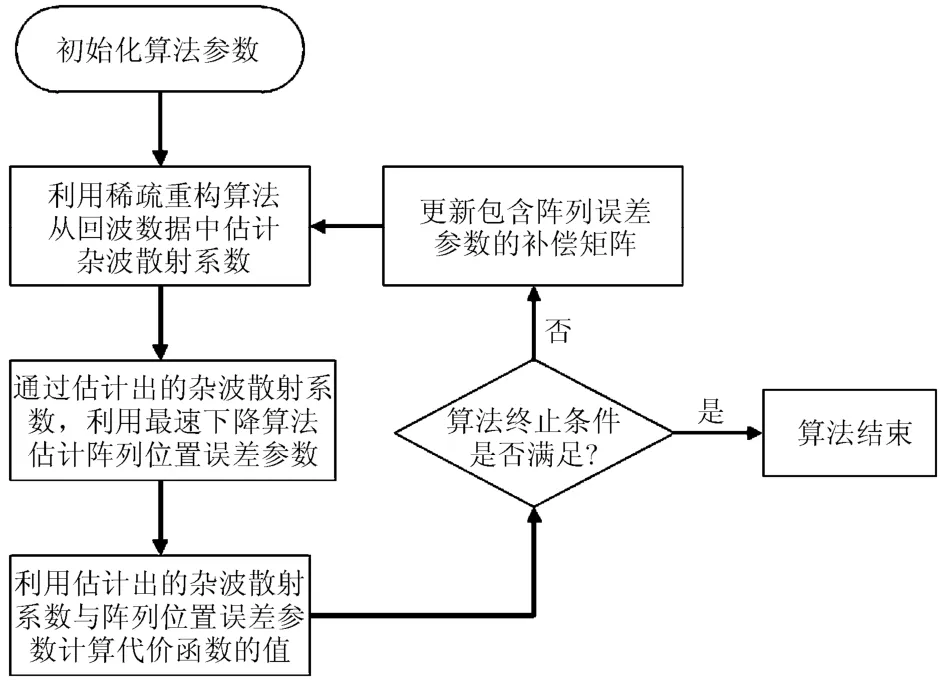
图2 算法流程图

将空间方位维离散化为Q个观测网格，设在第q个观测方向上，由阵元位置误差引起的发射阵列与接收阵列导向矢量误差分别为即其中N。对该观测方向上构造如式（9）所示的基矩阵。

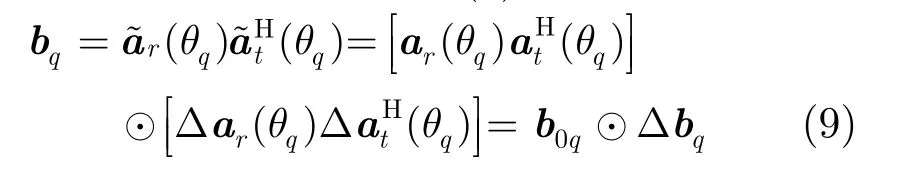
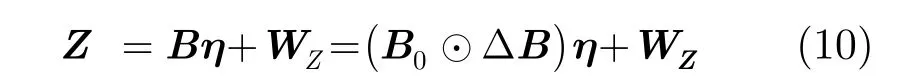
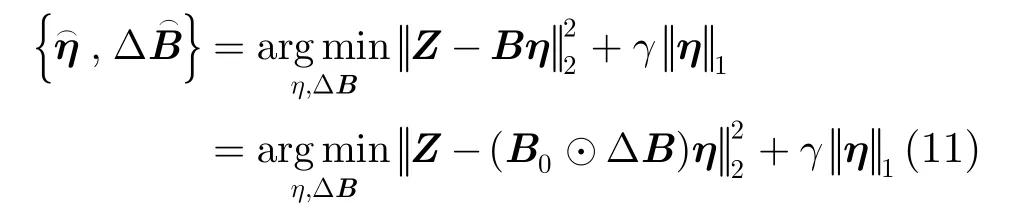
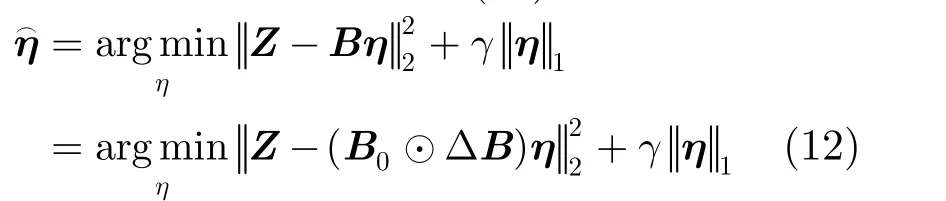
式（12）是一个凸优化问题，可采用 cvx工具包［19］对其进行求解。首先给定收发阵列位置误差的初值 ρ0，表达式为

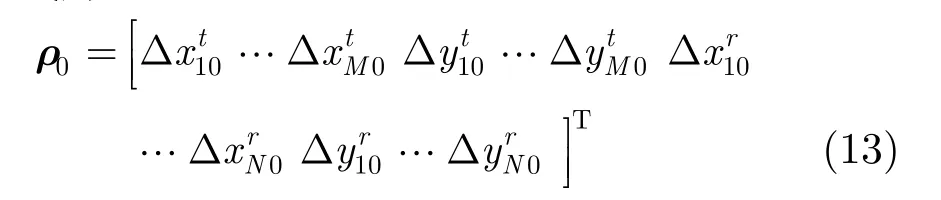
3.2 收发阵列位置误差估计

由上节的分析可知，在给定位置扰动初值的情况下，利用式（12）可以估计出场景杂波的散射系数。但是由于收发阵列存在位置误差，这将会导致接收数据Z和基矩阵B之间产生“失配”，故首先只能得到杂波散射系数的不︵精确估计。如果将上一步估计出的杂波散射系数η代入到代价函数中，继而估计出收发阵列位置误差参数用以更新补偿矩阵ΔB，如此便可以减小接收数据Z和基矩阵B之间的“失配”问题。若将更新后的补偿矩阵ΔB代入式（12）中再对杂波散射系数进行求解，便可提高其估计精度。下面介绍用最速下降算法实现对位置误差参数的估计。

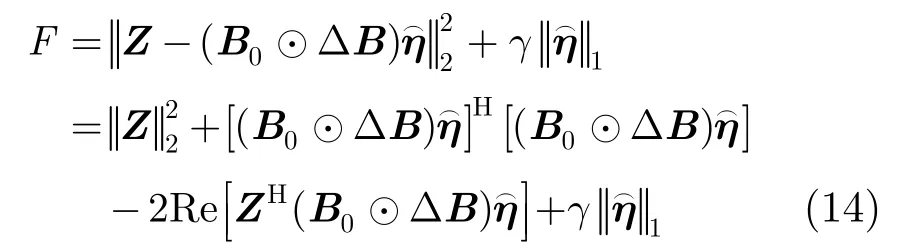
示为如式（15）所示的矩阵形式。

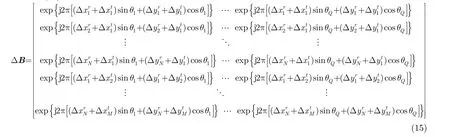
由式（15）可以看出中，补偿矩阵ΔB中包含了收发阵列位置误差参数。在本问题中，我们将所有阵列位置误差参数表示为如下的向量形式：

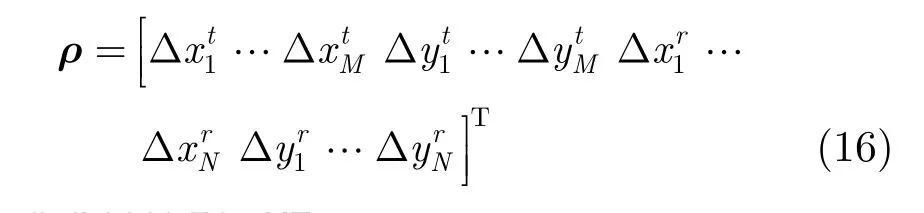
由链式求导法则可得

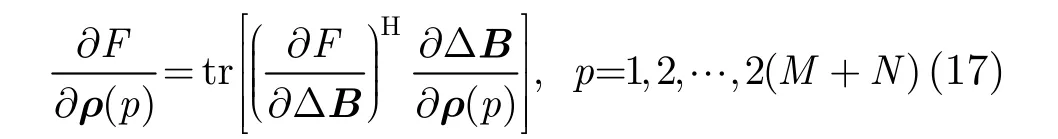
其中， ρ（ p）表示向量ρ中的第p个元素，tr（·）表示求矩阵的迹。记代价函数F对所有阵列位置误差参数求导的梯度向量为▽k，则其可以表示为

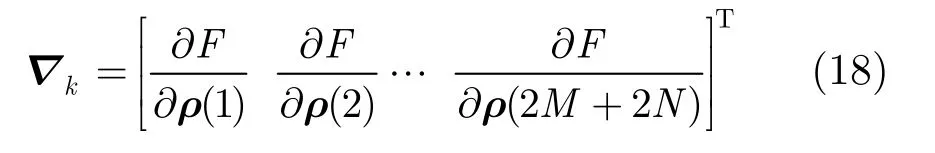
以最速下降法来求解阵列位置误差参数，给定位置误差参数初值 ρ0，则第 k+ 1次迭代时阵列位置误差参数的估计值可以表示为

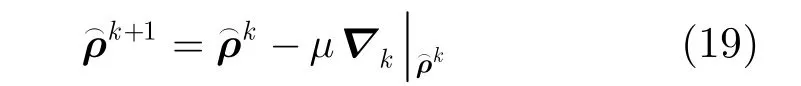
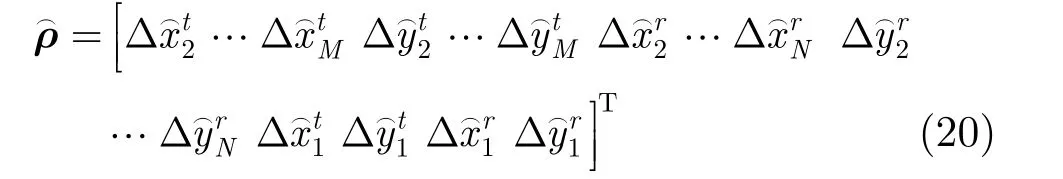
3.3 联合估计算法

将 3.2节所得阵列位置误差参数的估计值代入到补偿矩阵ΔB中，利用式（12）估计出新的杂波散射系数，将其代入到式（11）中，再次利用式（14）-式（19）估计出新的阵列位置误差参数，并将其代入到补偿矩阵中来更新基矩阵B。如此重复上述过程，便可以逐步提高阵列位置误差参数与杂波散射系数的估计精度。给定算法的最大迭代次数I，令 Fi和 Fi+1分别表示经过第 i- 1次和第i次迭代后代价函数的值，δ表示一个比较小的数，在经过第i次迭代

至此，我们提出了收发分置MIMO雷达收发阵列位置误差及杂波散射系数的联合估计算法。算法的主要流程概括如表1所示。

4 仿真实验

表1 阵列误差与杂波散射系数联合估计算法流程

实验 1本实验中考虑收发阵列都为半波间距的均匀线阵（ULA），且阵元个数均为16，发射阵列发射正交波形，信号码长为 256。将空间角度每间隔1°离散化为一个方位网格。假设在和 θ4= 40°4个角度存在强杂波散射点，其余空间方位为弱杂波散射点，且杂波分布事先未知，真实的杂波场景分布如图 3所示。收发阵元的位置扰动服从均值为 0，标准差为0.1λ的高斯分布。发射端和接收端理想的阵列流型以及存在位置误差时真实的阵列流型如图 4所示。本实验中杂噪比定义为

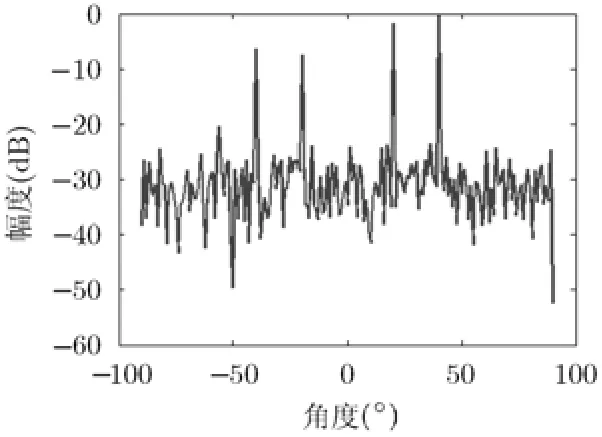
图3 真实杂波场景

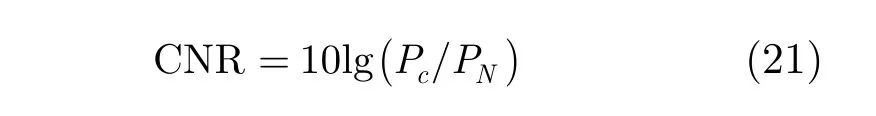
其中，Pc为阵列接收端接收到的杂波平均功率，PN为噪声功率。进行200次蒙特卡罗仿真实验，取CNR =30 dB，初始补偿矩阵ΔB为全1矩阵，搜索步长算法最大迭代次数 I= 300， ε=

图5给出了阵元位置的估计误差随着迭代次数的变化情况，纵坐标表示平均阵元位置估计误差与半波长 λ/ 2的百分比。在开始迭代之前，平均位置估计误差百分比为17.49，在经过170次迭代后算法收敛，平均位置估计误差百分比降为 0.1319。本实验中平均阵元位置估计误差表示经过当前次迭代后估计的阵元位置与真实的阵元位置之间的平均距离和，所有的距离均以半波间距 λ/ 2为量测单元。例如，平均阵元位置误差百分比为 17.49表示估计的阵元位置与真实的阵元位置之间的距离和除以总的阵元个数后的结果为 0.1749λ/ 2。平均阵元位置估计误差的计算公式可以用式（22）表示。

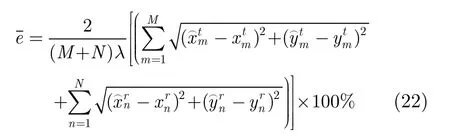
图6给出了发射端和接收端阵元位置真实值与阵元位置估计值的分布情况。由此可以看出，在收发阵列同时存在位置误差的情况下，利用本文所提出的迭代算法可以有效的估计出阵列误差。

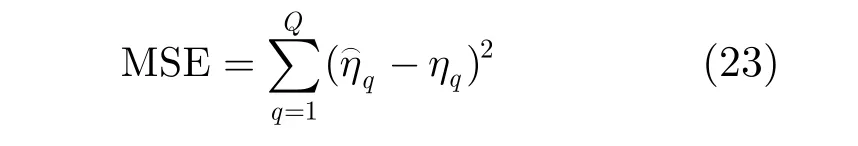
为验证杂波散射系数估计精度方面的性能，本文采用均方误差（MSE）作为衡量标准，被定义为其中，Q为空间方位离散角度的网格数。杂波散射系数估计的均方误差（MSE）随迭代次数的变化情况如图7所示，纵坐标表示散射系数估计的均方误差，在第1次迭代之前散射系数的均方误差为250.2，在经过最后一次迭代后，散射系数估计的均方误差下降到0.328。图7的结果表明，在阵列收发端同时存在位置误差的情况，本文算法可以有效地提高杂波点散射系数的估计精度。图8给出了杂波散射系数的真实值，估计值以及重构误差。图中结果表明在对杂波场景没有任何先验信息的情况下，本文算法可实现以较小的重构误差恢复出杂波散射系数。

实验 2为了进一步验证本文算法的有效性，下面分别以发射阵列和接收阵列的校正效果为例进行说明。本实验中的阵列位置误差与估计位置误差均采用实验1中的结果。

对于发射阵列，我们通过对比理想发射方向图与校正前后的发射方向图来验证校正效果。其中，发射方向图定义为

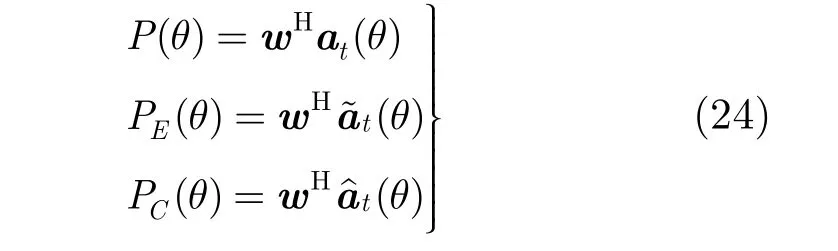
图4 发射端与接收端理想阵元位置与真实阵元位置

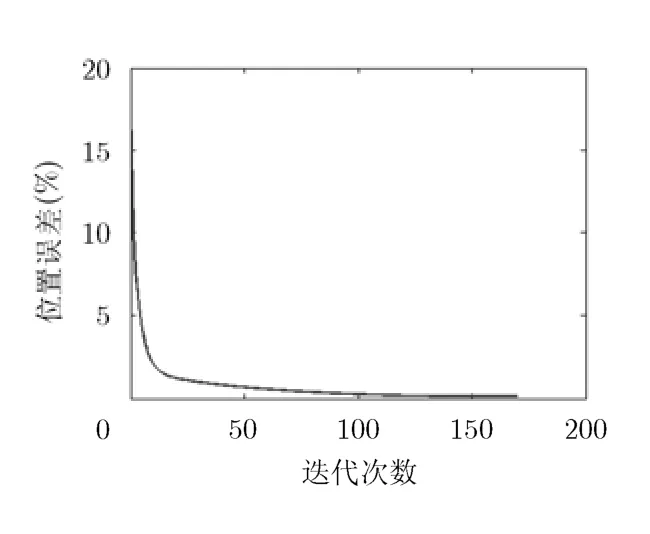
图5 阵元位置估计误差

式中，分别表示理想的发射方向图、发射天线存在位置误差时的发射方向图以及发射天线位置误差补偿后的发射方向图；w表示理想情况所得权值，其表达式为分别表示发射端理想情况下导向矢量、存在位置误差时导向矢量和经过位置误差补偿后的导向矢量。的表达式为

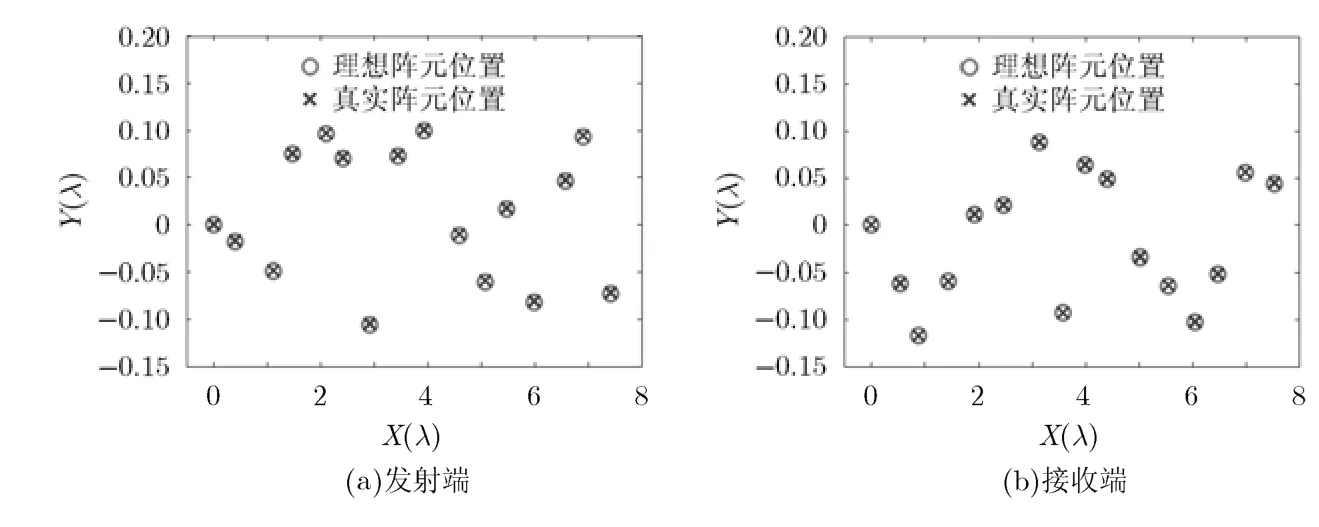
图6 发射端与接收端估计阵元位置与真实阵元位置

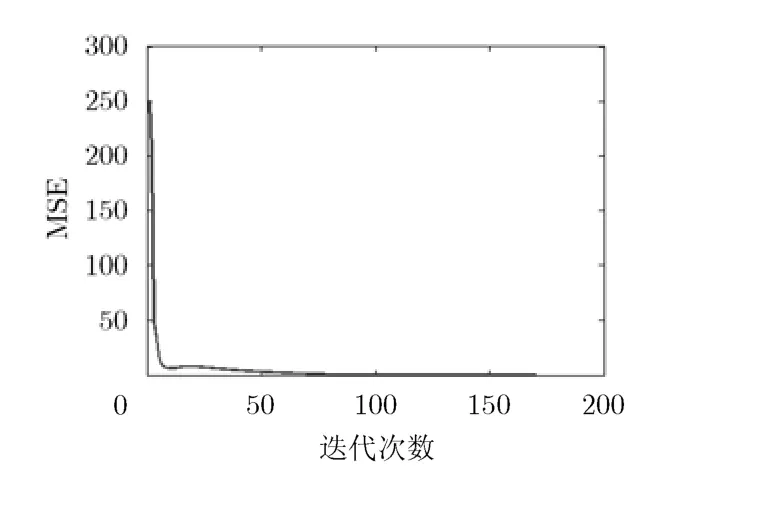
图7 散射系数估计均方误差

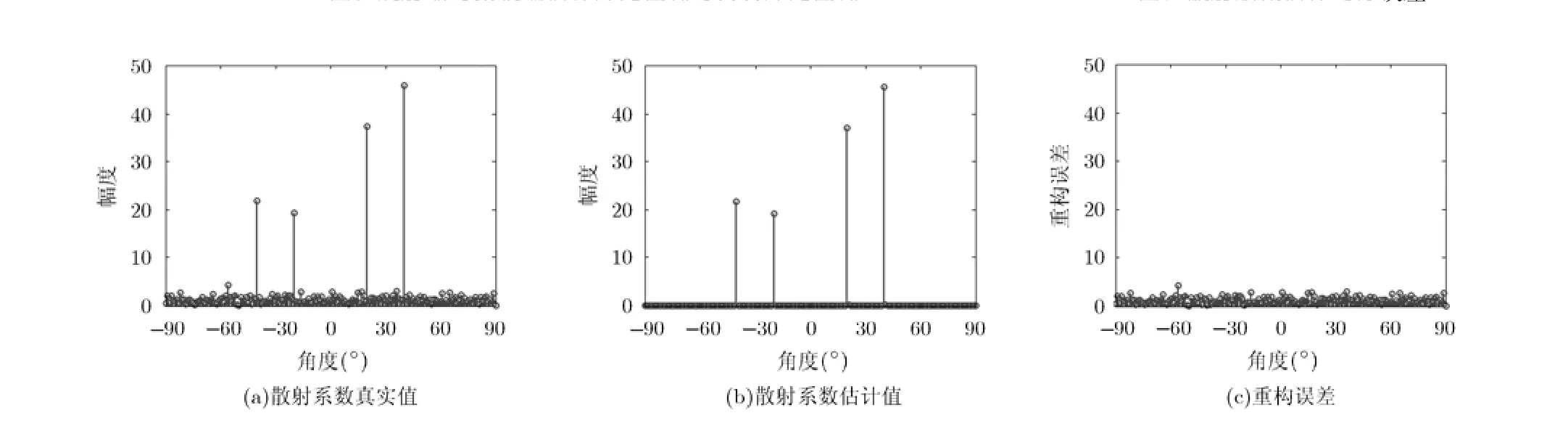
图8 杂波点散射系数真实值、估计值及重构误差

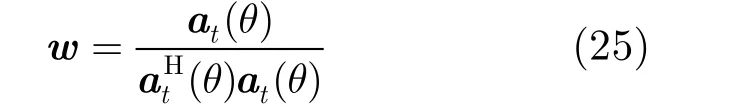
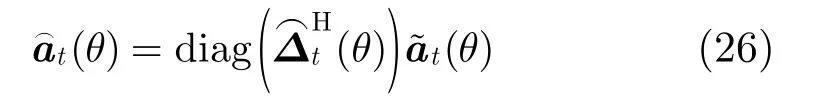
当期望发射方向图主波束指向30°时，图9分别给出了理想情况下综合出的发射方向图、发射天线存在位置误差时的发射方向图以及发射天线位置误差补偿后的发射方向图。由图9的结果可以看出，当发射天线存在位置误差时，发射方向图中不仅主波束方向产生了偏离而且副瓣电平明显抬高，而采用本文方法对阵列误差进行校正后，综合所得发射方向图与理想发射方向图十分接近。

对于接收阵列，我们采用 MUSIC算法来验证本文所提算法的有效性。此时假设空间中存在个等功率独立信源，信噪比为0 dB，快拍数为128。本实验中，MUSIC功率谱的定义如下：

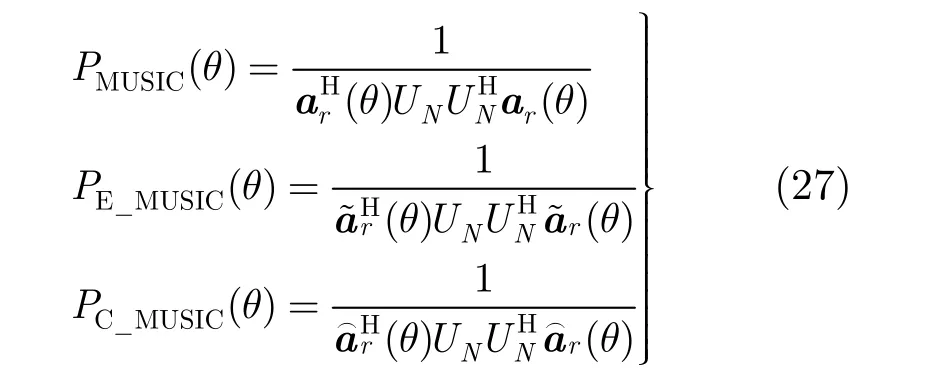
式中， UN为接收信号的噪声子空间， PMUSIC（θ），和分别表示理想的MUSIC功率谱、接收天线存在位置误差时的 MUSIC功率谱以及接收天线位置误差补偿后的MUSIC功率谱。的表达式为

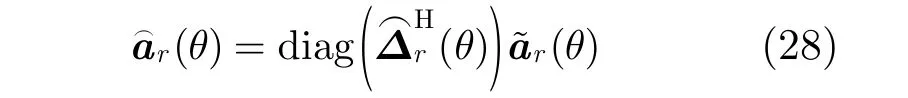
图10分别给出了理想情况下所得MUSIC功率谱及接收天线位置误差补偿前后所得 MUSIC功率谱。从这些结果可以看出，当接收天线存在位置误差时，MUSIC算法所得的谱峰会发生失真，偏离目标的真实角度，从而产生角度估计误差。而采用本文方法对阵列误差进行校正后，所得的功率谱与理想情况下的功率谱基本重合。从而验证了本文方法可以显著改善阵列位置误差带来的影响。

实验 3为了验证不同杂噪比条件下本文算法的有效性，下面分别取CNR从10～45 dB变化，其余仿真条件与实验1相同。本实验中，阵列位置估计的均方根误差（RMSE）被定义为

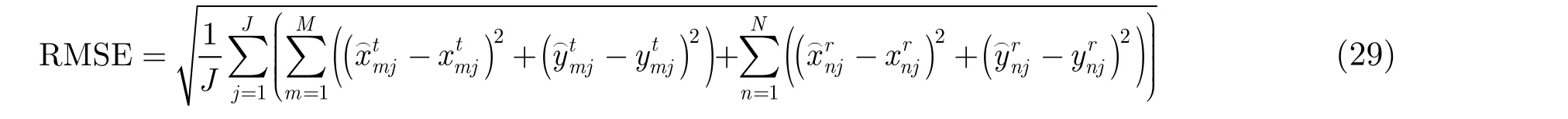
图11给出了阵元位置的估计均方根误差（RMSE）随CNR的变化曲线，由于一般情况下杂噪比较大所以实验中我们取CNR从10～45 dB变化。从图 11中的结果可以看出，在不同的杂噪比条件下，本文算法得到的收发端阵元位置估计的均方根误差变化不大，从而进一步说明了本文算法的有效性。

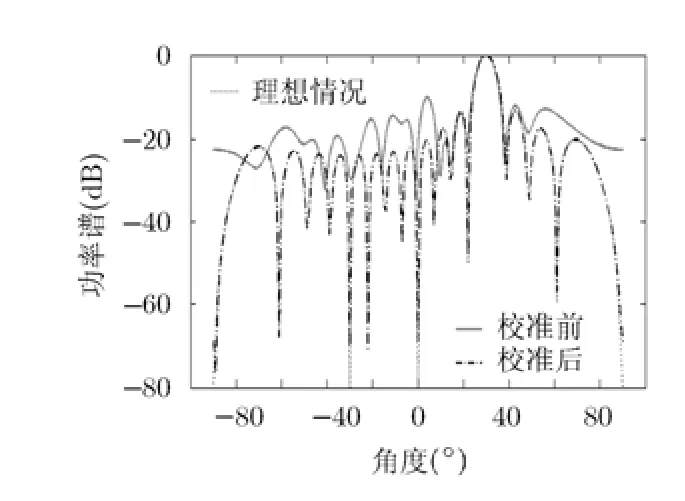
图9 波束指向30°时发射方向图

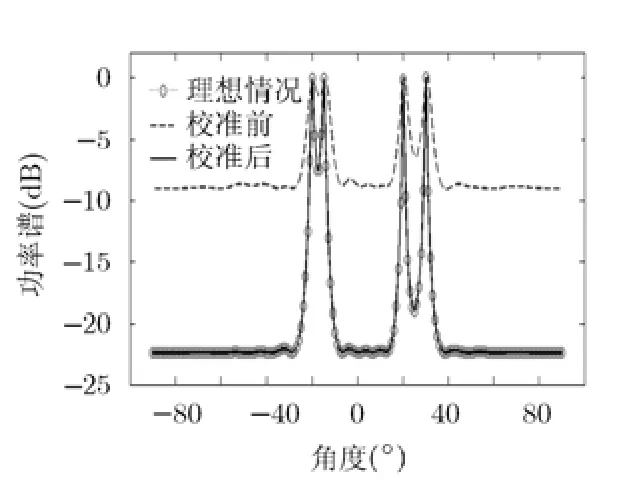
图10 MUSIC算法功率谱

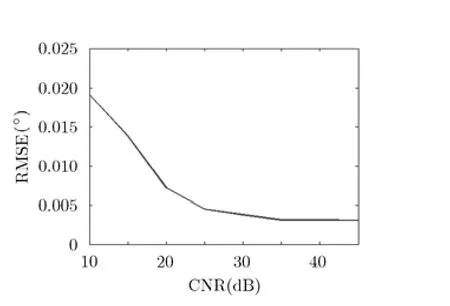
图11 位置估计均方根误差随CNR的变化曲线

5 结束语

本文提出一种基于杂波的收发阵列位置误差联合校正算法，该算法通过引入包含阵列位置误差的补偿矩阵，采用稀疏重构算法与最速下降算法交替迭代估计的方法，实现了杂波散射系数与收发阵列位置误差的联合估计。相比于传统的阵列误差校正方法，本文算法不需要特殊的外置辐射源，而是以易于获取的空间杂波作为校正“资源”，完成了对阵列收发端位置误差的同时校正。但是，本文在重构杂波场景时，假设场景中强杂波散射点是稀疏的，如何在各种更为复杂的杂波场景条件下完成阵列误差校正，还需进一步讨论和研究。

［1］ Li J and Stoica P. MIMO radar-diversity means superiority［C］. Proceedings IEEE 14th Annual Workshop on Adaptive Sensor Array Processing （invited）， MIT Lincoln Laboratory，Lexington， 2006: 1-64.

［2］ Li J， Stoica P， Xu L， et al.. On parameter identifiability of MIMO radar［J］. IEEE Signal Processing Letters， 2007， 14（12）: 968-971.

［3］ Hua G and Abeysekera S S. A comparison on DOA parameter identifiability for MIMO and phased-array radar［C］. IEEE International Conference on Information，Communications and Signal Processing （ICICS）， Tainan，2013: 10-13.

［4］ Babur G， Aubry P， and Le Chevalier F. Improved calibration technique for the transmit beamforming by a coherent MIMO radar with collocated antennas［C］. IEEE International Conference on General Assembly and Scientific Symposium（URSI GASS）， Beijing， 2014: 16-23.

［5］ Kashin V A and Mavrychev E A. Robust DOA estimation in MIMO radar with transmitting uncertainties［C］. IEEE Sensor Array and Multichannel Signal Processing Workshop（SAM）， A Coruna， 2014: 22-25.

［6］ Guo Y D， Zhang Y S， and Tong N N. ESPRIT-like angle estimation for bastatic MIMO radar with gain and phase uncertainties［J］. IET Electronics Letters， 2011， 47（17）: 996-997.

［7］ Friedlander B. Sensitivity analysis of the maximum likelihood direction-finding algorithm［J］. IEEE Transactions on Aerospace and Electronic Systems， 1990， 26（6）: 953-968.

［8］ 苏洪涛， 张守宏， 保铮. 发射阵列互耦及幅相误差校正［J］. 电子与信息学报， 2006， 28（5）: 941-944. Su Hong-tao， Zhang Shou-hong， and Bao Zheng. Mutual coupling， gain and phase error calibration for transmitting array［J］. Journal of Electronics & Information Technology，2006， 28（5）: 941-944.

［9］ 吴梦， 刘宏伟， 王旭. 一种循环迭代的MIMO雷达发射方向图设计方法［J］. 电子与信息学报， 2015， 37（2）: 322-327. Wu Meng， Liu Hong-wei， and Wang Xu. A cyclic method for MIMO radar transmit beampattern design［J］. Journal of Electronics & Information Technology， 2015， 37（2）: 322-327.

［10］ 王旭， 纠博， 刘宏伟， 等. 一种基于先验信息的MIMO雷达发射方向图设计方法［J］. 电子与信息学报， 2013， 35（12）: 2802-2808. Wang Xu， Jiu Bo， Liu Hong-wei， et al.. A Beampattern designmethod for MIMO radar based on a priori information［J］. Journal of Electronics & Information Technology， 2013，35（12）: 2802-2808.

［11］ Ng B C and Ser W. Array shape calibration using sources in known locations［C］. Proceedings of Singapore ICCS/ ISITA’92， Singapore， 1992: 836-840.

［12］ Boon C N and See C S. Sensor-array calibration using a maximum-likelihood approach［J］. IEEE Transactions on Antennas and Propagation， 1996， 44（6）: 827-835.

［13］ Weiss A J and Friedlander B. Array shape calibration using sources in unknown locations-a maximun likelihood approach［C］. IEEE International Conference on Acoustics，Speech and Signal Processing， New York， 1988: 11-14.

［14］ Li J F and Zhang X F. A method for joint angle and array gain-phase error estimation in bistatic multiple-input multiple-output non-linear arrays［J］. IET Signal Processing，2014， 8（2）: 131-137.

［15］ Li H B， Wei Q， Jiang J， et al.. Angle estimation and self-calibration for bistatic MIMO radar with mutual coupling of transmitting and receiving arrays［C］. IEEE Workshop on Electronics， Computer and Applications，Ottawa， 2014: 8-9.

［16］ Yu J and Krolik J. Adaptive phase-array calibration using MIMO radar clutter［C］. IEEE Radar Conference， Ottawa，2013: 1-5.

［17］ Donoho D L， Elad M， and Temlyakov V N. Stable recovery of sparse overcomplete representations in the presence of niose［J］. IEEE Transactions on Information Theory， 2006，52（1）: 6-18.

［18］ Sajjadieh M H S and Asif A. Compressive sensing time reversal MIMO radar: joint direction and doppler frequency estimation［J］. IEEE Signal Processing Letters， 2015， 22（9）: 1283-1287.

［19］ Grant M and Boyd S. CVX: Matlab software for disciplined convex programming［CP/OL］. http://stanford.edu/～boyd /cvx， 2008.

刘 源： 男，1989年生，博士生，研究方向为MIMO雷达信号处理、自适应信号处理.

纠 博： 男，1982年生，博士，副教授，研究方向为自适应信号处理、雷达自动目标识别、认知雷达.

刘宏伟： 男，1971年生，博士，教授，博士生导师，研究方向为雷达信号处理、雷达自动目标识别、认知雷达、协同探测.

夏香根： 男，1963年生，博士，教授，博士生导师，研究方向为空时编码、MIMO和OFDM系统、SAR和ISAR成像.

Joint Transmit and Receive Array Position Error Calibration for Bistatic MIMO Radar Based on Clutter

Liu Yuan①Jiu Bo①Liu Hong-wei①Xia Xia，ng-gen①②
①（National Laboratory of Radar Signal Processing， Xidian University， Xian 710071， China）
②（Department of Electrical and Computer Engineer， University of Delaware， Newark， DE 19716， USA）

The issue of position error estimation for transmit and receive array of a bistatic Multiple-Input Multiple-Output （MIMO） radar is investigated， and an algorithm for the joint estimation based on clutter echo is proposed. The algorithm is based on the criterion of minimizing the reconstruction mean-square error of clutter echo under the restraint of l1-norm of clutter coefficient. An alternately iterative and convex optimization algorithm is adopted to complete the estimation of clutter scattering coefficients and the position error of both transmit and receive arrays. The simulation results indicate the effectiveness of the proposed algorithm.

MIMO radar； Position error； Parameter estimation； Sparse reconstruction

s: The National Natural Science Foundation of China （61271291， 61201285）； The Fondamental Research Fund for the Cenfral Universities of China

TN958

A

1009-5896（2015）12-2956-08

10.11999/JEIT150347

2015-03-24；改回日期：2015-07-01；网络出版：2015-08-25

*通信作者：纠博 bojiu@mail.xidian.edu.cn

国家自然科学基金（61271291， 61201285）和中央高校基本科研业务费专项资金