可证安全的紧致无证书聚合签密方案

张玉磊王 欢李臣意张永洁王彩芬*（西北师范大学计算机科学与工程学院 兰州 730070）（甘肃卫生职业学院 兰州 730000）

可证安全的紧致无证书聚合签密方案

张玉磊①王 欢①李臣意①张永洁②王彩芬*①
①（西北师范大学计算机科学与工程学院 兰州 730070）②（甘肃卫生职业学院 兰州 730000）

无证书聚合签密不仅可以保证信息传输的机密性和认证性，还可以降低密文的验证和通信开销。分析现有无证书聚合签密方案，发现它们的计算效率普遍较低。该文提出一个紧致的无证书聚合签密方案，方案聚合验证密文信息需要的双线性对个数固定，并且与签密用户个数无关。与已有无证书聚合签密方案相比，新方案减少了双线性对运算个数，提高了聚合验证效率。同时，在随机预言模型下，基于双线性Diffie-Hellman困难问题和计算Diffie-Hellman困难问题，证明方案满足机密性和不可伪造性。

无证书签密；聚合签密；双线性Diffie-Hellman困难问题；计算Diffie-Hellman困难问题；公开验证

1 引言

签密可以同时实现加密和签名操作，保证消息的机密性和认证性，其效率优于传统“先签名后加密”方法。1997年，Zheng［1］首次提出签密的概念。2002年，Baek等人［2］首次描述签密方案的安全模型，并对文献［1］方案进行了严格的安全性证明。2008年，Barbosa等人［3］提出无证书签密概念并提出第1个无证书签密方案。自此，研究者们对无证书签密问题进行了一系列的研究［4-8］。

聚合签名［9］能够把多个用户对多个消息的签名聚合生成一个签名，验证者只需要验证聚合后的签名，就可以实现对多个签名用户的认证。无证书聚合签名［10，11］不仅可以克服传统公钥密码的证书管理问题和身份公钥密码的密钥托管问题，同时可以降低签名的验证开销和通信开销。为了提高通信效率和计算效率，需要对密文进行聚合传输和验证。2011年，Lu等人［12］提出第 1个无证书聚合签密方案（Certificateless Aggregate SignCryption， CLASC）。随后，Jiang等人［13］、张等人［14］和Eslami等人［15］分别提出新的CLASC方案。分析现有的4个CLASC方案，发现它们的聚合验证效率普遍较低。文献［12］和文献［14］的方案聚合验证密文数据时，需要（2n+2）个双线性对运算，文献［13］和文献［15］的方案聚合验证密文时，需要（n+3）个双线性对运算。

为了提高无证书聚合签密方案的验证效率，本文对文献［15］方案的签密算法进行了改进，提出了一个可证安全的紧致CLASC方案。与文献［15］方案相比，新方案不需要同步信息，并且聚合验证密文信息需要的双线性对个数固定，与签密用户个数无关。同时，在随机预言模型下，基于双线性Diffie-Hellman 困难问题和计算 Diffie-Hellman 困难问题，证明新签密方案满足机密性和不可伪造性。

2 CLASC方案形式化定义和安全模型

一般而言，CLACS方案包括密钥生成中心（Key Generation Center， KGC）、发送者 ui（ 1 ≤ i ≤n）、聚合者u和接收者 uB等用户，其中，聚合者收集用户ui对消息 mi的签密密文 δi并聚合生成聚合密文δ。

2.1 CLASC方案形式化定义

CLASC方案包括以下7个算法：

（1）系统建立算法：输入安全参数k，KGC输出系统主密钥s和系统参数Para。

（2）部分私钥生成算法：输入身份IDi、系统参数Para和主密钥s，KGC计算用户部分私钥 Di。

（3）用户密钥生成算法：用户选择秘密值 xi，输出用户的完整私钥和公钥 Pi。

（4）签密算法：输入消息 mi、身份IDi、私钥 Si、接收者的身份IDR及公钥 PR和系统参数Para，输出用户对 mi的签密密文 δi。

（5）聚合签密算法：输入发送者 ui对消息 mi的签密密文 δi，输出聚合密文δ，其中1 ≤ i ≤ n。

（6）聚合签密验证算法：输入聚合密文δ、发送者 ui的身份IDi及公钥 Pi、接收者的身份IDR及公钥 PR，验证密文δ的合法性。如果聚合密文正确，则输出真，否则输出假，其中1 ≤ i ≤ n。

（7）聚合解签密算法：若“聚合签密验证”算法输出真，则执行该算法。输入聚合密文δ、发送者 ui的身份IDi及公钥 Pi、接收者的身份IDR及私钥 SR，输出消息 mi，其中1 ≤ i ≤ n。

2.2 CLASC方案安全模型

2014年，文献［15］提出CLASC安全模型，但是该模型需要使用同步信息。本文方案不使用同步信息。CLASC方案必须考虑两类攻击者： AI和 AII。 AI一般指普通用户，它可以实现公钥替换攻击；AII一般指 KGC，它拥有系统主密钥可以进行伪造攻击。CLASC方案的安全性包括机密性和不可伪造性，因此，对于机密性和不可伪造性，必须分别考虑 AI攻击和 AII攻击。

定义 1如果 CLASC方案在敌手 AI和 AII的适应性选择密文攻击下是安全的，则该方案在适应性选择密文攻击下具有不可区分性［15］。

定义 2如果 CLASC方案在敌手 AI和 AII的适应性选择消息攻击下是安全的，则该方案在适应性选择消息攻击下具有存在不可伪造性［15］。

3 具体的CLASC方案

设安全参数为 k， q为大素数，定义生成元P ∈ G1。定义阶均为 q的群 G1和 G2，双线性映射e:G1×G1→ G2。哈希函数表示消息比特长度。

（3）用户密钥生成算法：用户 ui选择随机值产生用户的秘密值 xi。计算公钥用户的私钥为公钥为 Pi。

（4）签密算法：假定发送者Alice的身份、公钥和私钥分别为IDi， Pi，接收者 Bob的身份和公钥分别为IDR和 PR，其中1 ≤ i ≤ n。用户Alice执行以下步骤：

（c）计算 φ=H3（PPub）， ψ=H4（PPub）和hi= H5（Ri，

（5）聚合签密算法：聚合者输入Para、发送者 ui对应的身份列表IDi、公钥列表 Pi、消息 mi对应的签密密文接收者的身份IDR及接收者公钥 PR，其中1 ≤ i ≤ n。计算，则聚合密文为

（6）聚合签密验证算法：输入聚合签密密文δ、发送者 ui对应的身份列表IDi、公钥列表 Pi、接收者的身份IDR及接收者公钥 PR，执行以下步骤验证聚合签密密文的合法性。

（b） 验证下列等式是否成立：

如果等式成立，则输出“真”否则输出“假”。

（a）如果“聚合验证”算法输出为真，则接收者执行步骤（b），否则报错返回。

4 CLASC方案的安全性分析及效率对比

4.1 正确性

定理1CLASC方案是正确的

证明本文CLASC方案是正确的，当且仅当无证书签密密文 δi= （Ri， Ci，Si）和无证书聚合签密密文都是按照签密算法计算得到，并且有以下3类验证等式成立。

（1）验证者可以验证签密密文 δi= （Ri， Ci，Si）的正确性。

（2）验证者可以验证聚合签密密文 δ=（R1，的正确性。

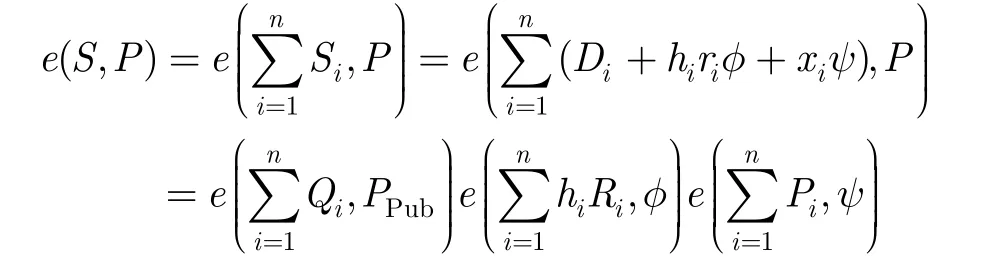
（3）接收者可以正确解密密文Ci。由于接收者可以计算：

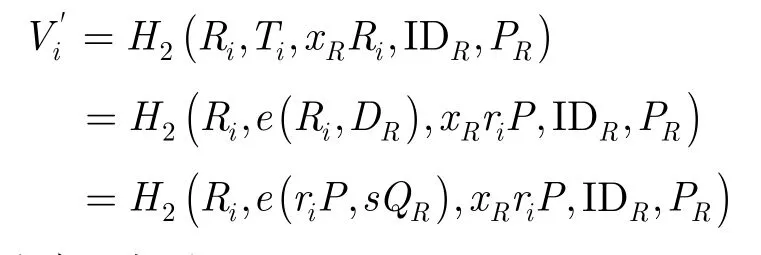
同时，由于

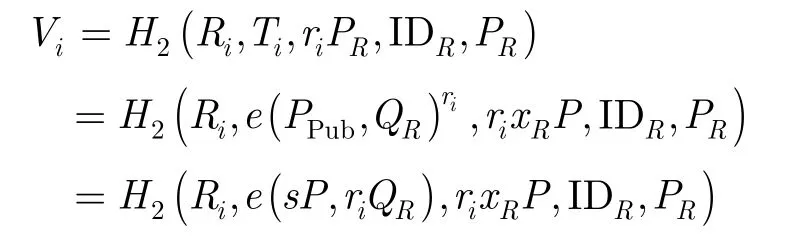
4.2 机密性

定理 2随机预言模型下，假设 BDH问题和CDH问题困难，则本文CLASC方案在适应性选择密文攻击下不可区分，即IND-CLASC-CCA2安全。

引理 1随机预言模型下，如果存在一个概率多项式时间攻击者 AI以不可忽略的概率赢得游戏，那么存在一个算法F能够解决BDH困难问题。

引理 2随机预言模型下，如果存在一个概率多项式时间攻击者 AII以不可忽略的概率赢得游戏，那么存在一个算法F能够解决CDH困难问题。

引理1和引理2的证明过程与文献［15］方案的机密性证明过程相似，限于篇幅，略去此部分。

4.3 不可伪造性

定理3随机预言模型下，假设CDH问题困难，则提出的CLASC方案在选择消息攻击下是存在性不可伪造的，即EUF-CLASC-CMA安全。

引理 3随机预言模型下，如果存在一个概率多项式时间攻击者 AI以不可忽略的概率赢得游戏，那么存在一个算法F能够解决CDH困难问题。

证明AI是攻击者，F是CDH问题挑战者。F给定一个CDH问题实例（P，aP，bP）， F的目标是使用 AI解决CDH问题，即计算abP。

初始阶段

F设 Ppub= aP， a为系统主密钥，系统参数为发送Para和 PPub给 AI。（F并不知道a的值）

攻击阶段

H1询问对于第i次非重复H1（IDi）询问：

（2）如果i = l， F计算 Qi= tib P，增加到表L1并返回Qi值（⊥表示不知道 tib的值）。

H3询问F保持表初始为空。AI询问H3预言机，若L3中存在询问项则直接返回，否则，F选择 θi∈ Z，返回 θiP并将 （PPub，θi）增加到表L3。

H4询问F保持表初始为空。AI询问H4预言机，若L4中存在询问项则直接返回，否则，F选择，返回 ηiP并将 （PPub，ηi）增加到表L4。

H5询问F保持表初始为空。F收到 AI对H5询问时，若L5已经存在相应项则直接返回。否则，F随机选择增加到表L5并返回hi值。

部分私钥询问对于第i次非重复询问用户ID的部分私钥，F运行H1询问并获得（i， IDi，ti）：i

（1）如果i = l，模拟终止。

公钥询问对于第i次非重复询问用户IDi的公钥，F随机选择计算返回Pi给 AI并将添加到L表中。

秘密值询问AI询问IDi的秘密值时，F查表L，若L表包含对应IDi，则返回相应值，否则F执行“公钥询问”询问，将添加到 L表并返回xi值。

公钥替换询问AI对IDi用新的公钥 P代替原公钥Pi。若L表包含身份IDi， F令若L表中未包含身份IDi， B执行“公钥询问”询问获得， F用更新表L。

H2询问F保持表初始为空。F收到 AI对（Ri，Ti， Wi， IDR，PR）的H2询问时（注意 Wi= riPR），对于输入（Ri，Ti， Wi， IDR，PR），F判断数据 （Ri，PPub，H1（IDi），Ti）对于DBDH预言机是否返回真，并且测试 e（Ri，PR）= e（P，Wi）等式是否成立，如果以上条件都成立，则F检查L2中是否存在对应条目若存在，则直接返回值Vi，否则F选择Vi∈ ｛0，1｝lm返回，并将（Ri，Ti，添加到表L2。

签密询问对于每个新的询问考虑两种情况：

（a） 如果IDi的公钥已经被替换，则执行过程：

①对IDi和ID'各自调用“公钥询问”获得公钥Pi和P'。

④查表 L3和L4获得 θP 和 ηPi的值，计算 hi=

（b）否则F利用xi和Di对mi正常签密，必要时需要进行秘密值询问和部分私钥询问。

（a）F对IDi和ID'各自调用“公钥询问”获得公钥Pi和P′。

（c）F检查表 L2，对于不同的 Wi寻找条目判断等式是否存在。如果该等式存在，即对应条目存在，F利用 Vi计算 Ci= Vi⊕ mi。否则 F随机选择并添加到表L2。

（d）F 检查表 L5获得 hi，并利用计算哈希函数H3（ ），然后F计算 Si=uaP其中η源于表L4。最后F返回 δi= （Ri， Ci，Si）。

伪造阶段

攻击者AI提交n个发送者的身份及对应的公钥、接收者的身份及对应的公钥、消息和伪造的聚合密文n

从攻击者AI的角度考虑，每个序号i有相同的其中1 ≤ i ≤ n。概率。不失一般性，从多个用户中选择一个作为目标用户，令则得到的聚合签密密文必须满足下列“聚合签密验证”等式。其中：则有

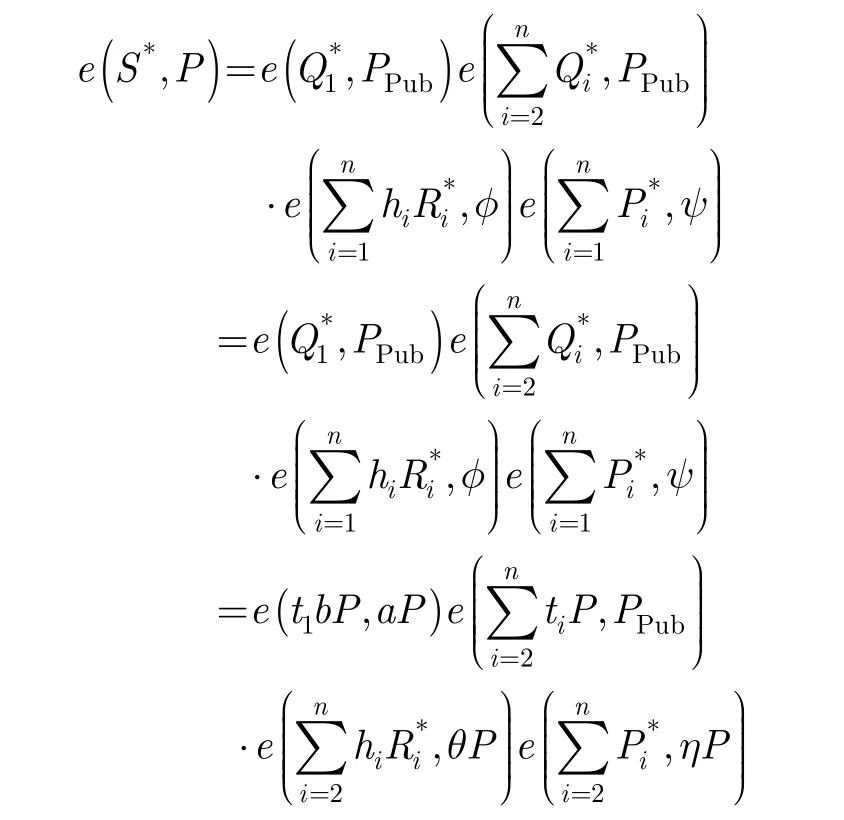
F要以计算abP：

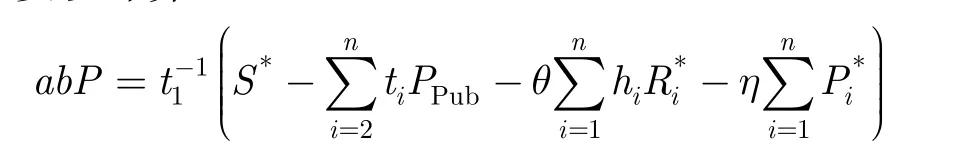
因此，F成功获得CDH困难问题的一个实例。与文献［11］相似，F能够成功解决CDH困难问题的优势为其中 qPPK

为部分私钥询问的次数。 证毕

引理 4随机预言模型下，如果存在一个概率多项式时间攻击者 AII以不可忽略的概率赢得游戏，那么存在一个算法F能够解决CDH困难问题。

证明AII是攻击者，F是CDH问题挑战者。F给定一个CDH问题实例（P，aP，bP）， F的目标是使用 AII解决CDH问题，即计算abP。

初始阶段

F设 PPub= sP， s为系统主密钥，系统参数为发送Para和s给 AII。

攻击阶段

H1询问对于第i次非重复H1（IDi）询问，F随机选择计算，增加到表L1并返回Qi值。

H3～H5询问与引理3相同。

公钥询问对于第i次非重复询问用户IDi的公钥，执行以下过程：

（

1）如果i = l，计算 Pi= tiaP，返回Pi给 AII将（IDi， ⊥， Pi）添加到L表。

秘密值询问AII询问IDi的秘密值时，F执行“公钥询问”询问获得（IDi，xi， Pi）。如果i ≠ l，则返回 xi；如果i = l，则

H2询问F保持表初始为空。F收到 AII对的H2询问时（注意Wi= riPR），执行以下操作：

（2）若存在，则直接返回值V；否则F随机选择i返回，并将添加到表L2。

注意：F对攻击者 AII和 AI关于H2的询问判断是不同的。 AII了解主密钥s，因此，这里F不需要判断数据对于DBDH预言机是否返回真。

签密询问对于每个新的询问（mi， IDi， IDR），考虑两种情况：

（a）F对IDR调用“H1询问”获得

（c）F检查表 L2，对于不同的 Wi寻找条目是否存在等式e（P，Wi）。如果该等式存在，即对应条目存在，F利用Vi计算 Ci= Vi⊕ mi。否则F随机选择并添加（Ri，Ti，Wi， IDR，PR，Vi）到表L2。

（d）F 检查表 L5获得 hi，并利用·（u P - ψ）计算哈希函数 H3（ ），然后 F计算 Si= Di+ uaP，其中 Di= sQi是部分私钥。最后F返回δi= （Ri， Ci，Si）。

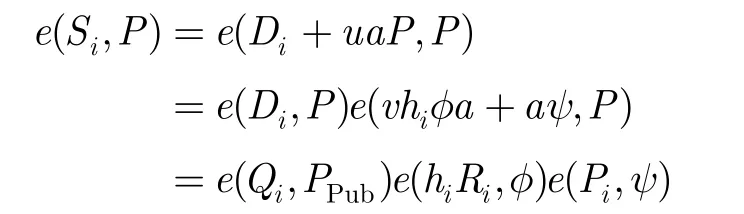
伪造阶段攻击者 AII提交发送者的身份 ID及对应的公钥P、接收者的身份 ID及对应的公钥 PR*、消息 mi*和伪造的聚合密文其中1 ≤ i ≤ n。

从攻击者 AII的角度考虑，每个序号i都有相同的概率。不失一般性，从多个用户中选择一个作为目标用户，令则得到的聚合签密密文必须满足“聚合签密验证”等式。其中则有

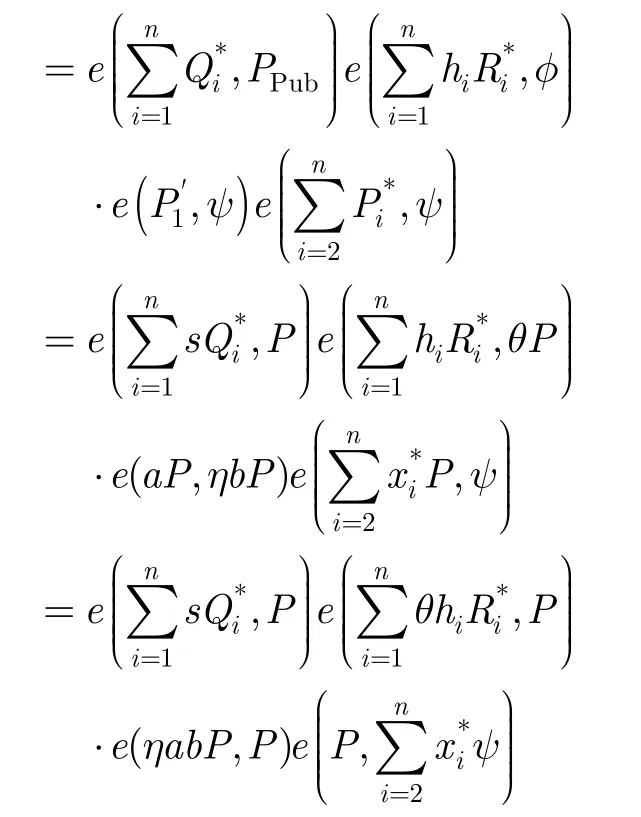
F要以计算abP：

因此，F成功获得CDH困难问题的一个实例。与文献［11］相似，F能够成功解决CDH困难问题的优势为其中qSV为秘密值询问的次数。 证毕

4.4 公开验证性

本文方案和文献［14，15］方案都支持聚合签密的公开验证。

而文献［12，13］方案不具有公开验证性。文献［12，13］方案验证聚合签密时需要使用秘密信息 Ti，但是只有接收者才可以计算 Ti，即通过 Ti= e（Ri，DR）计算秘密信息Ti，一般用户无法计算该值。因此，文献［12，13］方案中第三方无法验证聚合签密密文的有效性。

4.5 效率分析

分析现有的无证书聚合签密方案，发现它们的聚合验证效率普遍较低。以P表示双线性对运算个数，n表示参加签密的用户数。

由表1可知，文献［12～14］方案需要（2n+2）个双线性对运算，文献［15］方案使用“同步信息”将对运算数减少到（n+3）个，但是，它们方案的对运算数和签密用户数相关，不具有紧致性。本文方案验证聚合签密密文时，只需要4个双线性对运算，并且，对运算个数与签密用户数无关，因此，本文方案的效率较高，并且是一个紧致的无证书聚合签密方案。本文方案与文献［12～15］方案性能对比如表1所示。

表1 无证书聚合签密方案性能对比

5 结束语

无证书聚合签密CLASC结合了无证书签密和聚合签名技术的优势，能够对签密信息进行聚合传输和批验证，具有一定的应用需求。例如，车载自组织网络中数据的秘密聚合传输。本文提出了一个紧致的无证书聚合签密方案，该方案验证聚合签密密文时，只需要4个双线性对运算，对运算个数与签密用户数无关。同时，在随机预言模型下，基于BDH困难问题和CDH困难问题证明方案满足机密性和不可伪造性。

［1］ Zheng Yu-liang. Digital signcryption or how to achieve cost（signature & encryption） ＜＜ cost （signature） + cost（encryption）［C］. Proceedings of the Cryptology-CRYPTO1997， California， USA， 1997: 165-179.

［2］ Baek J， Steinfeld R， and Zheng Yu-liang. Formal proofs for the security of signcryption［C］. Proceedings of the Cryptology-PKC2002， Paris， France， 2002: 81-98.

［3］ Barbosa M and Farshim P. Certificateless signcryption［C］. Proceedings of the ASIACCS2008， New York， USA， 2008: 369-372.

［4］ 孙银霞， 李晖， 李小青. 无证书体制下的多接收者签密密钥封装机制［J］. 电子与信息学报， 2010， 32（9）: 2249-2252. Sun Yin-xia， Li Hui， and Li Xiao-qing. Certificateless signcryption KEM to multiple recipients［J］. Journal of Electronics & Information Technology， 2010， 32（9）: 2249-2252.

［5］ Weng Jian， Yao Guo-xiang， Robert Deng， et al.. Cryptanalysis of a certificateless signcryption scheme in the standard model［J］. Information Science， 2011， 181（3）: 661-667.

［6］ 光焱， 顾纯祥， 祝跃飞， 等.一种基于LWE问题的无证书全同态加密体制［J］. 电子与信息学报， 2013， 35（4）: 988-993. Guang Yan， Gu Chun-xiang， Zhu Yue-fei， et al.. Certificateless fully homomorphic encryption based on LWE problem［J］. Journal of Electronics & Information Technology，2013， 35（4）: 988-993.

［7］ Zhou Cai-xue， Zhou Wan， and Dong Xi-wei. Provable Certificateless generalized signcryption scheme［J］. Designs，codes and Cryptography， 2014， 1（2）: 331-346.

［8］ Shi Wen-bo， Kumar N， Gong Peng， et al.. Cryptanalysis and improvement of a certificateless signcryption scheme without bilinear pairing［J］. Frontiers of Computer Science， 2014， 8（4）: 656-666.

［9］ Boneh D， Gentry C， Lynn B， et al.. Aggregate and verifiably encrypted signatures from bilinear maps［C］. Proceedings of the Cryptology-EUROCRYPT2003， Warsaw， Poland， 2003: 416-432.

［10］ 明洋， 赵祥模， 王育民. 无证书聚合签名方案［J］. 电子科技大学学报， 2014， 43（2）: 188-193.Ming Yang， Zhao Xiang-mo， and Wang Yu-ming. Certificateless aggregate signature scheme［J］. Journal of University of Electronic Science and Technology of China，2014， 43（2）: 188-193.

［11］ 张玉磊， 周冬瑞， 李臣意， 等. 高效的无证书广义指定验证者聚合签名方案［J］. 通信学报， 2015， 36（2）: 2015033. Zhang Yu-lei， Zhou Dong-rui， Li Chen-yi， et al.. Certificateless- based efficient aggregate signature scheme with universal designated verifier［J］. Journal on Communications， 2015， 36（2）: 2015033.

［12］ Lu Hai-jun and Xie Qi. An efficient certificateless aggregate signcryption scheme from pairings［C］. Proceedings of International Conference on the Electronics， Communications and Control （ICECC）， Ningbo， China， IEEE， 2011: 132-135.

［13］ Jiang Yi， Li Jian-ping， and Xiong An-ping. Certificateless aggregate signcryption scheme for wireless sensor network［J］. International Journal of Advancements in Computing Technology， 2013， 5（8）: 456-463.

［14］ 张雪枫， 魏立线， 王绪安. 无证书的可公开验证聚合签密方案［J］. 计算机应用， 2013， 33（7）: 1858-1860. Zhang Xue-feng， Wei Li-xian， and Wang Xu-an. Certificateless aggregate signcryption scheme with public verifiability［J］. Journal of Computer Applications， 2013， 33（7）: 1858-1860.

［15］ Eslami Z and Nasrollah P. Certificateless aggregate signcryption: security model and a concrete construction secure in the random oracle model［J］. Journal of King Saud University Computer and Information Sciences， 2014， 26（3）: 276-286.

张玉磊： 男，1979年生，博士，副教授，研究方向为密码学与信息安全.

李臣意： 男，1989年生，硕士生，研究方向为密码学与信息安全.

张永洁： 女，1978年生，硕士，副教授，研究方向为密码学与信息安全.

王彩芬： 女，1963年生，博士，教授，博士生导师，研究方向为密码学与信息安全.

Provable Secure and Compact Certificateless Aggregate Signcryption Scheme

Zhang Yu-lei①Wang Huan①Li Chen-yi①Zhang Yong-jie②Wang Cai-fen①①
①（College of Computer Science and Engineering， Northwest Normal University， Lanzhou 730070， China）②（Gansu Health Vocational College， Lanzhou 730000， China）

Certificateless aggregate signcryption not only can ensure the confidentiality and authentication of information transmission， but also can reduce the cost of data communication and the verification of ciphertexts. Through analyzing some existing certificateless aggregate signcryption schemes， it is found that their efficiencies are much lower. A provable secure certificateless compact aggregate signcryption scheme is proposed in this paper. In the new scheme， the pairing numbers， not depending on the number of signcryption users， are constant when aggregate ciphertexts are verified. Compared with the existing certificateless aggregate signcryption schemes， the new scheme decreases pairing numbers and raise the efficiency of verification. Moreover， based on the assumption of bilinear Diffie-Hellman and computational Diffie-Hellman， in the random oracle model， it is proved that the new scheme satisfies the properties of confidentiality and unforgeability.

Certificateless signcryption； Aggregate signcryption； Bilinear Diffie-Hellman problem； Computational Diffie-Hellman problem； Public verification

s: The National Natural Science Foundation of China （61163038， 61262056， 61262057）； The Higher Education Science Research Foundation of Gamsu Provice（2015B-220）； The Young Teacher’s Scientific Research Ability Promotion Program of Northwest Normal University （NWNU-LKQN-12-32）

TP309

A

1009-5896（2015）12-2838-07

10.11999/JEIT150407

2015-04-08；改回日期：2015-07-03；网络出版：2015-08-28 *通信作者：王彩芬 wangcf@nwnu.edu.cn

国家自然科学基金（61163038， 61262056， 61262057），甘肃省高等学校科研项目（2015B-220）和西北师范大学青年教师科研能力提升计划项目（NWNU-LKQN-12-32）