汽车转向泵支架的拓扑分析及可制造优化

尹存宏

(贵州交通职业技术学院，贵州贵阳 550001)



汽车转向泵支架的拓扑分析及可制造优化

尹存宏

(贵州交通职业技术学院，贵州贵阳 550001)

对汽车转向泵支架进行有限元分析，阐述对其进行拓扑优化的必要性；在此基础上，建立了以支架结构柔度最小作为目标函数、以优化后剩余体积作为约束函数的拓扑优化数学模型，并建立拓扑优化的有限元模型，运用HyperWorks软件对支架进行了拓扑优化计算。根据零件的可制造化处理准则并结合支架的制造工艺对优化结果进行了可制造化处理，获得了一个结构更合理且性能更佳的新支架。新支架的质量为4.35kg，相比原支架减少16.35%。对新支架进行刚度和强度的分析，并与原支架有限元分析结果进行对比，结果显示：其强度、刚度以及一阶模态频率均有所提高，满足支架使用的轻量化要求。

转向泵支架；拓扑优化；可制造化；轻量化

0　引言

随着经济的高速发展，传统能源的供不应求和环境恶化带来的负面效应越来越突出，而汽车数量的迅猛增加更使这些问题越发变得严重，因而，轻型、节能、环保、安全、舒适以及低成本是所有汽车生产商所追求的方向，特别是环保更是与人类可持续发展的重大问题息息相关，节能减排问题已成为汽车制造业亟待解决的重要课题。

实践表明：汽车的整车质量下降10%，其燃油效率便能够提高6%～8%；在环保方面，可减少尾气排放4%～10%；在制动性方面，刹车距离可减少5%；在动力性方面，加速到100km/h的时间可降低8%；耐久性方面，可以降低50%的疲劳破坏。

文中针对广汽菲亚特某新型汽车主要载荷情况和边界约束条件以及极限典型工况重新设计其转向泵支架，重点是运用三维结构拓扑优化技术[1]的变密度法来寻求支架在确定的载荷和约束条件下，刚度和材料在设计空间内最佳的分布形式[2]，结合HyperWorks有限元分析软件对其进行结构拓扑优化设计及可制造优化。

1　原支架有限元分析

作为影响汽车转向系统的关键部位，转向泵支架对转向泵起着支撑的作用并安装在发动机上，其性能的好坏直接影响到汽车的转向安全性和操作稳定性。原支架的质量约5.2kg，对其进行材料和边界条件约束后，施加工况，运用Workbench14.0软件进行结构分析，所得到的等效Misses应力云图和变形云图如图1及图2所示，模态云图如图3所示。

从图1可以看出：转向泵支架在此工况下所受到的最大等效应力为92.66MPa，位于红色MAX处，构件的大部分等效应力在20MPa以下。构件所采用的材料为铝合金材料ADC12，其屈服强度等于172MPa，此构件的安全系数为1.86，机械构件的安全系数范围为1.3～1.5[3]，因此此构件的安全系数大于规定的安全系数范围，支架的强度满足使用要求。

从图2可以看出：转向泵支架在此工况下的最大变形0.270 5mm，位于图中红色MAX处。由于本支架所受到的极限工况是弯曲工况，其弯曲刚度由支架的挠度来评价，依据设计使用手册规定，受弯构件的允许挠度为2.41，因此变形量小于支架的许用挠度，满足刚度需求。

从图3可以看出：支架的一阶模态频率为729Hz。汽车在行驶过程中受到两类激振,频率大小如下：(1)发动机怠速引起的，其振动频率范围在33Hz以上[4],发动机的最大转速为7 500r/min,由f=n/60(Hz)得最大回转频率为125Hz;(2)行驶中地面给汽车的激振频率，大约为0～50Hz[5]。由分析结果可知支架的固有频率远大于在行驶中受到的激振频率，因此，支架不会产生共振现象，具有足够的模态刚度。

综上分析可得出：此支架的材料用量偏多，在强度和刚度上过于安全，尚存在优化的空间。因此运用Optistruct优化软件对其进行拓扑分析，提高材料的利用率，得到更为合理的设计。

2　支架的拓扑优化设计

2.1拓扑数学模型的建立

在对转向泵支架进行拓扑优化设计时，为了能使支架具有较大的刚度，常选择支架的柔度作为优化的目标函数。优化目标为泵支架的柔度最小，即支架的刚度最大。选用变密度法进行拓扑优化设计，所以选择设计区域中各单元的相对密度作为设计变量。选择优化后的体积作为约束函数，即优化后体积与优化前体积之比。厂家所要求的目标是体积至少减少20%，即体积比是0.8，为了得到较为理想的优化结果，作者采用体积比0.75作为优化约束条件。

转向泵支架的拓扑优化的数学模型为:

求X={X1,X2,…,Xn}T

MinC=FTU

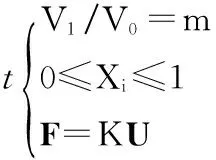
(1)

式中：Xi(i=1,2,…，n)是设计变量(此式中是每个微单元的相对密度);C是结构的柔度;F是荷载矢量;U是变形位移矢量;m是剩余材料体积的百分比;V1是优化后结构剩余材料的总体积;V0是结构设计区域的体积;K是结构的系统刚度矩阵。

在实际工程中，柔度的大小常用应变能的大小来判别，应变能等于使物体变形过程中所做的功。在HyperWorks软件中结构应变能C由下列公式计算：

C=1/2uTff=Ku

或C=1/2uTKu=1/2∫εTσdV0

(2)

式中：K为系统的刚度矩阵;f为载荷;u为载荷f作用下的节点位移矢量;ε是在载荷f的作用力下结构的应变；σ是应力。

常认为应变能是结构刚度的倒数，当载荷给定后，结构应变能小则意味着系统的刚度大。应变能须与静态子工况(载荷工况、载荷步)相联系。

所以，对于转向泵支架的拓扑优化，采用基于SIMP材料插值模型的变密度法[6]，以结构刚度最大为优化目标函数，体积分数作为约束条件，在Optistruct中采用结构应变能最小来表示优化目标。

2.2有限元模型的建立

2.2.1确定拓扑优化空间

对汽车转向泵支架进行拓扑优化，首先是要定义支架的优化设计空间，在支架的设计空间中可以根据需要任意布置支架材料。定义支架的设计空间原则是：保证优化后的泵支架不与其他结构发生干涉；尽量避免对支架以外的结构进行重新设计从而降低相应模具的再开发成本；考虑装配等实际要素，取尽量大的区域，以便能够充分地对支架进行优化，挖掘其优化潜力。

如图4所示，绿色部位是转向泵支架的非优化区域，因为它们是承载转向泵的位置以及承载转向泵支架的部位；紫色部位是转向泵支架的优化区域，它们是转向泵支架的非支撑及承载位置。

2.2.2支架材料

因支架性能的好坏直接影响到汽车的转向安全性和操作稳定性，所以支架材料需具有较高的屈服强度和抗拉强度以及低的应力集中敏感性，铝合金材料ADC12(国产牌号YL113)能够满足这些基本性能。ADC12的材料属性参数如表1所示。

表1　支架材料ADC12属性

2.2.3边界及工况条件

为了能够真实准确地描述结构本身的实际约束情况，在螺栓孔周围将所有的节点通过刚性单元(RBE2)连接在一起，RBE2单元是没有质量的单元，连接比较容易，且接近实际结构受力特性。厂家所给的极限工况状况是汽车行驶在颠簸道路上的情景，此时受到的最大惯性力为Z向-5g，作者运用达朗贝尔原理将惯性力转变为静态力施加在支架上。除此之外，车架所承受的力还包括：转向泵的重力19N(考虑到惯性因素，此工况所受重力应是原重力的5倍)，均匀分布在4个支撑孔位置；皮带的最大压轴力1 200N,方向与水平方向成45°夹角；安装在7 000r/min的发动机支架上面。如图5所示。

2.3优化结果

分析数值在optistruct中的设置如图6所示，其中体积比(volumefrac)为0.75，离散参数(DISCRETE)为2.5。通过拓扑优化设置的参数进行迭代计算，经过数次迭代之后得到了拓扑优化的结果，优化的最终结果就是设计域内各个单元的相对密度，支架的拓扑优化得到的相对密度分布云图如图7所示。

图中深红色部分是相对密度趋于1的单元，是拓扑优化最终需要保留的部分，其余彩色部分是相对密度在0.3以上的单元，也即过渡单元，0.3以下的单元已被删除。可看出红色部位与彩色部位的边界划分总体比较清晰，且离散度比较高，中间过渡的单元不多，形成了比较明确的结构形式，所以迭代结果满足设计要求。

3　可制造化设计

为了充分利用拓扑优化所得的结果，最大程度提高新支架的刚度以及减少自重，新支架的材料分布应尽量忠实拓扑优化的结果。对拓扑优化结果的一些不合理的部分要进行修改。因优化后单元的相对密度不全是“0”或“1”，还存在一些中间密度值，需要人为增加或删除材料，使这些单元变为极值形式的“0”或“1”类型。

此支架是铸造件，铸造件的设计不仅要满足其力学性能的要求，还需满足合金材料的铸造性能、铸造工艺对结构的要求。结构设计合理与否，影响着铸件的质量、制造成本以及生产率。对拓扑结果进行可制造化设计后，得到新的支架如图8所示。

4　新支架验证

为验证可制造化处理后得到的新转向泵支架的静态和动态性能，需要对其进行有限元分析，计算其刚强度及模态，对比新支架和原支架的性能，分别如图9—11所示。

从图中可以看出：新支架在极限工况下所受到的最大应力为60.275MPa，位于图中MAX处，小于铝合金材料ADC12的屈服强度172MPa，折合成安全系数为2.85，大于机械构件的安全系数范围，大于原支架的安全系数，可知结构的设计更加合理，支架的强度满足使用要求。

由转向泵新支架的模态计算结果可知：新支架的弹性固有频率(即第8阶固有频率)是936.82Hz，高于原支架的一阶固有固有频率，也属于高频振动，并且远离发动机的回转频率以及地面的激振频率，可以有效避免共振现象，满足动态特性的要求，具有足够的模态刚度。

5　结论

采用基于SIMP材料插值模型的变密度法对汽车的转向泵支架进行了拓扑优化设计和有限元分析验证，取得了较好的效果。将结构拓扑优化分析方法应用到汽车零部件的轻量化设计中，可以克服传统设计中的盲目性，在改善或保持结构性能的基础上大大减轻结构的质量。

【1】周克民，李俊峰，李霞.结构拓扑优化研究方法综述[J].力学进展，2005，35(1)：69-75.

【2】罗震，陈立平，黄玉盈，等.连续体结构的拓扑优化设计[J].力学进展，2004(34):463-476.

【3】阮帅帅,谭丕强.发动机连杆的有限元分析及结构优化[J].制造业自动化，2011(10):110-113.

【4】黄琳.起重机伸缩臂结构优化研究[D].大连：大连理工大学，2007.

【5】张胜兰，郑冬黎.基于Hyperworks的结构优化设计技术[M].北京：机械工业出版社，2007.

【6】张东旭.连续体结构拓扑优化及形状优化若干问题[D].大连：大连理工大学，1992.

TopologyAnalysisandManufacturabilityOptimizationforAutomotiveSteeringPumpBracket

YINCunhong

(GuizhouPolytechnicCollegeofCommunications,GuiyangGuizhou550001,China)

Thoughfiniteelementanalysis(FEA)ontheautomotivesteeringpumpbracket,theneedtooptimizethetopologyoforiginalbracketwassetforth.Themathematicmodelofthebracketfortopologyoptimizationwasestablishedtotakeitsminimumstructuralflexibilityasobjectivefunctionandtotakeoptimizedremainingcubageastheconstraintfunction.Moreoverthefiniteelementmodelofthetopologyoptimizationwasestablished,andsoftwareHyperWorkswasusedforitstopologyoptimizedcalculationofthebracket.Accordingtothemanufacturabilityprocessprincipleofsect1s,andcombiningwithmanufacturingprocessofbracket,theoptimizationconsequenceofmanufacturingprocesswascarriedout,resultinginanewbracketwithmorerationalstructureandbetterproperty.Thenewbracket’sweightwas4.35kg,andthereductionofbracket’sweightwasabout16.35%ascomparedtooriginal.Thenewbracket’sintensityandrigiditywereanalyzed,andwerecomparedwiththoseofFEAtotheoriginalbracket.Theresultsshowthatnewbracket’sintensity,rigidityandthefirst-ordermodalfrequencyareallimproved,whichmeetusagerequirementsoflightweightofthebracket.

Steeringpumpbracket;Topologyoptimization;Manufacturability;Lightweight

2015-03-31

尹存宏(1989—)，硕士研究生，主要研究方向为先进制造技术、机械设计及理论。E-mail:13984356487@163.com。