基于iSIGHT集成技术的某重卡双轴转向机构多目标优化
周红妮,冯樱,赵慧勇,朱林
(湖北汽车工业学院汽车工程学院,湖北十堰 442002)
基于iSIGHT集成技术的某重卡双轴转向机构多目标优化
周红妮,冯樱,赵慧勇,朱林
(湖北汽车工业学院汽车工程学院,湖北十堰 442002)
针对东风某重卡汽车在使用中存在的轮胎异常磨损问题,利用ADAMS/View对双轴转向机构进行建模与运动学仿真。基于多学科设计优化(MDO)软件iSIGHT,实现ADAMS/View运动学仿真集成,并建立机构优化分析流程。采用正交数组DOE分析法和NSGA-II遗传算法实现了该双轴转向机构的多目标优化。优化结果表明:优化后各车轮转角误差大大减小,有效解决了车轮异常磨损问题。
双轴转向机构;iSIGHT集成;ADAM/View运动仿真;遗传算法;多目标优化
0 引言
近年来,随着双轴转向汽车的广泛使用,一些典型故障相继而出,主要表现在转向车轮异常磨损问题上。国内学者针对汽车双轴转向机构的设计与优化问题已有较多的研究,也相继提出了许多优化设计方法和理论[1-10]。在运动学和动力学仿真分析方面,利用多体动力学仿真软件ADAMS及其Insight模块对双轴转向进行优化设计,已成为较为通用的研究方法[3-7]。但是在解决复杂系统的多学科多目标优化问题方面,基于参数的多学科设计优化软件iSIGHT软件却更胜一筹。iSIGHT软件具备广泛的CAD/CAE及自编程序集成接口,可方便用户建立复杂系统仿真分析流程,通过集成的各种设计分析与优化算法,自动实现多学科多目标工程问题的设计分析与优化,大大缩短了产品的开发周期、降低研发成本[13]。目前,iSIGHT已成为国际上先进的工程优化软件,在各行业领域应用广泛。在我国汽车行业,利用iSIGHT软件建立多学科设计优化研究与应用平台,已在各大高校和企业逐步展开。
文中针对东风某双轴转向重卡汽车在使用中存在的轮胎异常磨损问题,基于iSIGHT软件集成优化技术,建立双轴转向机构ADAMS/View仿真分析流程,并应用DOE分析方法与多目标优化遗传算法对机构进行优化。作者将计算机仿真集成优化技术及多目标优化方法应用到汽车双轴转向系统的设计研究中,有效解决了轮胎异常磨损的实际问题,可为今后汽车复杂系统的设计、开发提供新的有效途径。
1 双轴转向机构运动学仿真
1.1ADAMS/View建模
通过对样车进行3D扫描及逆向建模,如图1所示,提取双轴转向机构各关键点的坐标值。其中坐标系定义如下:ZX平面为车辆的纵向对称平面,Y轴通过一轴两主销中心点连线,与ZX平面垂直,交点为原点O;Y轴指向驾驶员右侧,X轴通过点O平行于地面并指向车辆后方,Z轴垂直向上。在ADAMS/View中,将各关键点用杆件连接,并添加运动副,建立的双轴转向机构运动学仿真模型如图2所示,其中各硬点坐标已实施参数化,为后续机构优化设计提供模型准备。
1.2车轮转向运动规律
为避免车轮磨损,应保证各车轮转向时都尽量作纯滚动,也就是第一轴与第二轴所有车轮转向运动应满足运动协调关系,即满足阿克曼转向原理[8-10]。根据图3所示,转向轮转角关系如下式:
(1)
cotβ1-cotα1=B/L1
(2)
cotβ2-cotα2=B/L2
(3)
式中:αi为第i轴左轮转角,i=1,2;βi为第i轴右轮转角,i=1,2;Li为第i轴轴线至第三、四桥轴线中心线间的距离,i=1,2;B为两主销中心点之间的距离。
由上式可推导出二轴左轮、一轴右轮、二轴右轮对一轴内轮的理论转角关系:
α2=arctan((L2/L1)·tanα1)
(4)
β1=arccot(cotα1+B/L1)
(5)
β2=arccot((L1/L2)·cotα1+B/L2)
(6)
1.3运动学仿真
在ADAMS/View中的前转向垂臂旋转副处施加驱动,并通过软件的测量功能(Measure)测出4个车轮的实际转角,同时根据式(4)—(6)得到相对一轴右轮变化时其他转向轮的理论转角。通过运动仿真,得到一轴右轮、二轴左轮、二轴右轮随一轴左轮转动时,实际转角关系与理论转角关系间的绝对误差,如图4所示。可知:随着一轴左轮的转动,此双轴转向机构使得其他3个车轮的实际转角关系与阿克曼理论转角关系存在一定误差,其中二轴的左、右两轮转角误差都相对较大,在-35°~35°转角范围内,随着一轴左轮的转动误差增大超过5°,右转到极限位置,误差增幅更明显,达到14°。较大的转角误差是导致车轮异常磨损的主要原因,因此有必要对此转向机构进行优化设计。
2 iSIGHT集成ADAMS/View应用程序
iSIGHT具备广泛的CAD/CAE集成接口,能够快速建立复杂的仿真流程,并提供设计优化所需的各种算法,包括DOE实验设计、优化算法、近似模型、蒙特卡洛分析等,根据设定的设计变量和优化目标,可自动进行分析循环和寻优计算[13]。将ADAMS/View应用程序集成到iSIGHT中,有2种方式:(1)通过Simcode程序集成组件;(2)通过iSIGHT ADAMS组件集成。文中采用Simcode程序集成方式,这种集成方式较为通用,是一个完整地将应用程序输入、执行、输出进行集成的接口。它本质上包含:用于改写程序的输入文件DataExchanger模块、执行应用程序的OS Command模块和用于读取输出文件的DataExchanger模块。在集成之前要准备好3个ADAMS/View文件:runadams.bat批处理文件、*.cmd命令行文件(此为iSIGHT需要解析的input文件)、*.bin模型文件。在Simcode组件中定义好input、command、output三部分,通过测试运行后,就可实现ADAMS/View运动学仿真集成,如图5所示。
3 实验设计DOE
3.1设计变量与优化目标
由于轮距、轴距、主销中心点位置、车轮定位参数、转向垂臂与车架铰接点的位置等会影响到整车性能与布置,一般不做大范围的调整。考虑到实际机构调整和改进的可行性,主要从各杆件的长度和定位夹角进行转向机构的优化。表1为初选的设计变量,共14个。

表1 设计变量初值与上下偏差
在双轴转向机构参数优化设计时,应当使各车轮转角的实际值与理论值尽可能接近。根据汽车行驶的实际情况,要求转向机构初始位置附近的误差比在极限位置时要小,以减小在常用位置或车轮常用转角(通常车速较高)时轮胎的磨损。文献[2-4]引入加权函数描述不同转角范围内对转向轮转角误差的要求;文献[5]以各轮转角绝对误差的平均值作为目标函数;文献[6-7]以各轮转角绝对误差或绝对误差的最大值作为目标函数。由于加权函数法受设计者主观因素影响较大,且随车型变化加权函数也会不同,将各轮转角绝对误差的最大值作为目标函数没有考虑汽车常用行驶工况,优化结果的实际意义有待研究。因此综合考虑,以一轴右轮、二轴左轮、二轴右轮随一轴左轮转动时,各车轮实际转角与理论转角间的绝对误差的平均值最小作为优化目标,即3个优化目标。将其描述成适用于iSIGHT软件的3个目标函数,如式(7)—(9)所示:
(7)
(8)
(9)
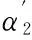
3.2设计变量DOE分析
将DOE组件添加到图5所示的Task组件即可在iSIGHT中形成设计变量DOE分析流程。iSIGHT软件提供了多种DOE方法,如:参数试验、全因子/部分因子设计、正交数组、中心组合设计、拉丁超立方、优拉丁超立方等。由于正交数组方法数据点分布均匀、齐整可比,试验次数相对较少,且能进行各因素对响应的交互作用分析,是一种高效、快速和经济的实验设计方法,因此采用正交数组法(Orthogonal Arrays),对表1中的设计变量(因子)对3个目标响应进行DOE分析,以选择合理的优化变量。图6所示Pareto图为设计变量对3个目标响应的影响结果。
DOE分析中,Pareto图反映了所有因子对响应的贡献率,蓝色的条形表示正效应,红色则表示负效应。由图6可知:各设计变量对3个目标响应效果并不完全一致,存在相互冲突现象,其中对3个目标响应影响较大的因子有DV_1、DV_2、DV_3、DV_5、DV_7、DV_10、DV_13,可选择这7个因子作为优化变量。
4 转向机构多目标优化
4.1多目标优化问题
实际工程优化问题大多数属于多目标优化问题,各子目标之间一般是相互冲突的,某子目标的改善可能引起其他目标的降低,即同时使多个目标均达到最优一般是不可能的。解决多目标问题的最终目的只能是在各个目标之间进行协调权衡和折中处理,使各子目标均尽可能达到最优。法国经济学家V Pareto最早研究了经济学领域内的多目标优化问题,提出了Pareto解集的概念。由于多目标优化问题中各子目标是相互冲突的,优化解不可能是单一解,而是一个解集,称为Pareto最优解集,对应的目标函数空间的像称为Pareto前沿。就目标函数而言,这些解之间是无法比较优劣的。求解多目标优化问题就是要毫无偏好地找到尽可能多的具有代表性的符合要求的Pareto最优解,在计算得到均匀分布的Pareto最优解之后,根据设计要求和工程实际经验,从中客观地选择最满意的优化结果[11-13]。
对文中双前桥转向机构的优化,欲使各车轮转角的实际值与理论值尽可能接近,机构的设计必须尽可能满足式(7)—(9)所示的3个子目标,形成一个多目标优化问题。
目前,多目标优化方法有归一化方法和非归一化方法两种。归一化方法以加权法为代表算法。而非归一化方法是采用Pareto机制直接处理多个目标的优化技术,它不需要将多个目标转化为单一目标,避免了归一化方法存在的诸多问题,并能使所求解集前沿与Pareto前沿尽量接近、均匀覆盖。
4.2优化计算
遗传算法(MOGA)是非归一化方法的代表,研究应用较为广泛。遗传算法通过对一个种群进行运算操作,在一个进化代中可以得到多个Pareto最优解,是求解Pareto最优解集的一种有效算法。多目标遗传算法NSGA-II(非支配排序遗传算法)是NAGA算法的改进,由于在普通遗传算法中导入了“拥挤距离”和“拥挤距离排序”的方法,在非支配排序中,接近Pareto前沿的个体被选择,使得Pareto前进能力增强,算法探索性能优良。文中选择NSGA-II遗传算法对双轴转向机构进行优化。
在iSIGHT软件中,将优化组件添加到图5所示的Task组件中,即可形成iSIGHT优化计算流程。将上述DOE分析得到的7个设计变量选择为优化变量,并设置合理的变化范围,以式(7)—(9)所示的3个函数作为优化目标,并选择NSGA-II遗传算法,设置算法种群个体数为32,进化30代,交叉概率为0.9,可进行960次迭代计算。
4.3结果分析
通过优化计算得到图7所示优化目标3D散点图。图7中多个蓝色个体为求解得到的Pareto解集,在三维目标函数空间相图中形成Pareto前沿。根据实际情况,玫红色个体为最终选择的Pareto最优解。表2为优化前、后优化变量的变化值。
图8为优化后各车轮转角绝对误差的变化情况。与优化前(图4)相比:优化后各车轮转角绝对误差大大减小,其中二轴左、右车轮转角绝对误差在-35°~35°内减小最为明显,误差均小于1°;在大转角时误差增大的情况下,仍能使最大误差与优化前相比明显降低,最大不超过6°。这样一轴左轮从中间位置转动到两侧极限位置过程中,特别是在常用转角范围内,可使各车轮实际转角关系与阿克曼理论转角关系尽量地接近,将有效解决轮胎的异常磨损问题。
5 结论
利用iSIGHT软件实现了双轴转向机构ADAMS/View运动学仿真的集成,并采用正交数组DOE分析方法合理选择了优化变量,最终利用NSGA-II多目标遗传算法实现了双轴转向机构的多目标优化设计,有效降低了轮胎异常磨损。由于引起轮胎磨损的原因有多种,综合多工况多因素进行转向系统的多目标优化设计需要进一步深入研究。文中将多学科设计优化软件iSIGHT集成技术成功应用于转向机构的多目标优化设计中,解决了轮胎异常磨损的实际问题,可为今后汽车复杂系统的设计、开发提供新的途径和研究基础。
【1】孙靖民.机械优化设计[M].北京:机械工业出版社,2004.
【2】宁介雄,周海霞.汽车摇臂机构的数学建模及最优化[J].机械设计,2007,24(2):65-67.
【3】刘振声,赵亮.双前桥转向系与悬架运动协调性分析及优化[J].中国机械工程,2013,24(16):2164-2167.
【4】袁夏丽,王金员.多轴转向系统的运动学仿真及优化设计[J].机械科学与技术,2014,33(12):1795-1797.
【5】朱林,冯樱,严运兵.基于响应面法的双前桥转向机构参数优化[J].湖北汽车工业学院学报,2013,27(1):1-4.
【6】胡敏锋.双前桥汽车转向机构优化[D].长沙:湖南大学,2013.
【7】李庆欢,张代胜,吕召全.基于ADAMS的双前桥重型汽车双摇臂设计及优化[J].合肥工业大学学报:自然科学版,2006,29(1):80-83.
【8】Mu Chunyan,Yu Jingnuo,Yang Yuyan,et al.Design for Dual-front Axle Steering Angle of the Heavy Truck[C]// International Conference on Ducational and Network Technology,2010:185-187.
【9】He Yusheng,Xiong Tingchao.Design and Analysis of Multi-axle Steering System of Heavy Duty Vehicle[R].SAE paper 931919,1993:160-166.
【10】Miller Gerald,Reed Robert,Wheeler Fred.Optimum Ackerman for Improved Steering Axle Tire Wear on Trucks[R].SAE paper 912693,1991:572-578.
【11】Wei Fengtao,Song Lili,Yan Liupeng.Application of iSIGHT in Solving Multi-objective Optimal Design Problems[C]//International Conference on Consumer Electronics,Communications and Networks,2011:110-113.
【12】Srinivas N,Deb K.Multi-objective Function Optimization Using Non-dominated Sorting Genetic Algorithms[J].Evolutionary Computation,1995,2(3):221-248.
【13】赖宇阳.Isight参数优化理论与实例详解[M].北京:北京航空航天大学出版社,2012.
Multi-objective Optimization on Dual-axle Steering Mechanism of a Heavy VehicleBased on Integration Technology of iSIGHT
ZHOU Hongni, FENG Ying, ZHAO Huiyong, Zhu Lin
(School of Automotive Engineering, Hubei University of Automotive Technology, Shiyan Hubei 442002,China)
Aiming at the tire abnormal wearing problem of a Dongfeng heavy vehicle, the simulation model of the dual-steering mechanism was established by using ADAMS/View, and the kinematics simulation results shown that it existed great errors between real wheel angle and theory wheel angle. The integration of kinematics simulation to ADAMS/View was achieved and the optimal analysis process of the steering mechanism was established based on multidisciplinary design optimization (MDO) software iSIGHT. With orthogonal array DOE analysis, the dual-steering mechanism was optimized by applying multi-objective optimization genetic algorithm NSGA-II. The optimization results show that the wheel angle error is decreased greatly after the optimization, so the tire abnormal wearing problem is solved effectively.
Dual-steering mechanism; iSIGHT integration; ADAM/View kinematics simulation; Genetic algorithm; Multi-objective optimization
2015-03-18
湖北省教育厅科学研究重点项目(D20122302);汽车动力传动与电子控制湖北省重点实验室(湖北汽车工业学院)资助项目(ZDK1201403)
周红妮(1981—),女,硕士,讲师,主要从事汽车动力学仿真及控制、汽车优化技术等方面的研究工作。E-mail:179471631@qq.com。

