二能级原子自发辐射过程中的Wigner-Yanase偏态信息

刘万芳,尹训昌,付 静,李 敏

(1.安庆师范学院 物理与电气工程学院,安徽 安庆 246011;2.吉林建筑大学城建学院,长春 130111;3.集美大学诚毅学院,福建 厦门 351100)



二能级原子自发辐射过程中的Wigner-Yanase偏态信息

刘万芳1,尹训昌1,付 静2,李 敏3

(1.安庆师范学院 物理与电气工程学院,安徽 安庆 246011;2.吉林建筑大学城建学院,长春 130111;3.集美大学诚毅学院,福建 厦门 351100)

研究单个二能级原子自发辐射过程中原子和光场Wigner-Yanase的信息变化,并分别计算原子和辐射场的Wigner-Yanase信息.结果表明：原子和光场的Wigner-Yanase信息均依赖于平均值〈Sz〉;当原子处于基态时,光场的Wigner-Yanase信息达到最大值;原子与光场并非同步达到最大混合态.

二能级原子;自发辐射;Dicke模型;Wigner-Yanase偏态信息;混合态

自以量子纠缠为基础的量子隐形传态方案提出以来[1],量子信息科学已引起人们广泛关注,在进行量子通讯[2]过程中,Wigner-Yanase偏态信息可较好地刻画一个系统的信息量[3-4].纯态中Wigner-Yanase偏态信息对应某个算符的涨落,若体系的量子态用密度算符描述,则其体现了某个算符与密度算符的不对易程度.由于Wigner-Yanase偏态信息是量子Fisher信息特殊的一类[5],因此其与不确定度[6-7]和系统参数估计及量子纠缠[8]有关.在2个量子比特纯态中,通过定义一个广义的Wigner-Yanase偏态信息,即与完全concurrence等价[9]；在多粒子体系中,通过粒子间的相互作用,可提高该体系的Wigner-Yanase偏态信息[9-10]；在量子记忆与信息存储系统中,当光场信息转移至原子系综时,可通过Wigner-Yanase偏态信息刻画光场信息的减少与原子系综信息的增加[11].

光场与原子构成的复合系统在纠缠态的制备、纠缠度的浓缩、量子计算、量子态的保真和压缩转化中应用广泛[12-15],但对复合系统及两个子系统在光场与原子发生相互作用时的信息变化研究较少,本文针对单个处于激发态的二能级原子与真空场构成的复合系统,在原子自发辐射至基态的过程中,讨论光场与原子两个子系统Wigner-Yanase偏态信息的变化.

1 Wigner-Yanase偏态信息

文献[16]利用局部的Wigner-Yanase偏态信息定义了量子关联,若给定体系的状态为ρ,则观测量Ak的偏态信息表达式[3]为

(1)

由式(1)可见:对于一个孤立体系,若其状态变化遵守Landau-von Neumann方程,则该体系的信息保持一个常数；当两个不同系综合并时,联合系综的信息将小于分系综信息的平均值；当两个不同的组成部分构成复合系统时,复合系统的信息可分为两部分信息之和.

式(1)体现了算符Ak和量子态ρ之间的不对易程度.对于纯态,体系的状态可用波函数ψ描述,若与波函数ψ对应的密度矩阵ρn=ρ,则偏态信息为

(2)

即算符Ak的涨落.

1.1单个量子比特总的Wigner-Yanase偏态信息

利用Bloch球表示单个量子比特,在退相干机制下,文献[17]讨论了量子Fisher信息的演化特性.若单个量子比特的总自旋为S,则相应的3个自旋算符Sx,Sy,Sz满足的对易关系为

(3)

基于偏态信息的定义,引入一总偏态信息

(4)

(5)

式(5)即为单个量子比特偏态信息的上限.若单个量子比特处于最大的混合态,则单个量子比特的偏态信息有一个为零的下限,由于最大混合态可用密度矩阵

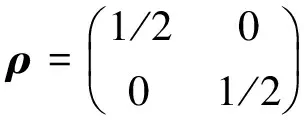
(6)

描述,且该密度矩阵与任何二维矩阵均具有对易的特点,因此

(7)

即处于最大混合态的单个量子比特有一个值为零的下限偏态信息.

1.2玻色系统总的Wigner-Yanase偏态信息

对于玻色系统,利用产生湮灭算符a+和a定义两个厄米算符分别为

(8)

即算符X1和X2为描述玻色系统两个正交分量的算符,并满足对易关系

(9)

由偏态信息的定义可定义玻色系统的总偏态信息为

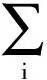
(10)

玻色系统纯态的总偏态信息为

(11)

由于任意两个粒子数态|m〉和|n〉等概率混合对应的密度矩阵并非与任意算符均对易,因此与二能级原子的情况不同.

2 单个二能级原子自发辐射过程中的偏态信息

在Weisskopf-Wigner自发辐射理论下,量子腔中一个处于激发态|+〉的原子可以任意频率释放一个光子而回到基态|-〉,原子与腔的相互作用可用Hamilton量[18]描述为

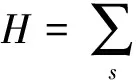
(12)

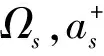
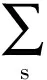
(13)

若原子初始时刻处于激发态|+〉,腔场处于真空态|0〉,则任意时刻腔场原子体系的状态可表述为

(14)

将式(14)代入Schrödinger方程可得概率幅c+(t)和c-,s(t)满足的方程为

(15)

若所有的模式频率接近,则式(13)中的求和可换为积分

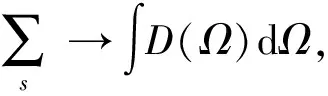
(16)

其中D(Ω)为终态态密度,该态密度和耦合强度g(Ω)分别与Ω的某次幂成比例.通过计算可得

(17)

其中γ与原子的寿命相关.

2.1二能级原子的偏态信息

通过对光场求迹计算原子的约化密度矩阵

(18)

可得原子的偏态信息,利用总的偏态信息定义,将3个算符对应的偏态信息相加可得

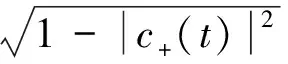
(19)

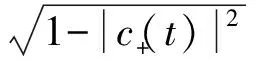
(20)

考虑到Sz的平均值为(cos2θ-sin2θ)/2,则可将式(20)转化为

(21)

2.2辐射场的偏态信息

若处于激发态|+〉的原子可以任何频率辐射一个光子回到基态|-〉,则光场以概率pssin2θ处于频率为Ωs的|1s〉态,与其对应的密度矩阵为

(22)

(23)

代入相应的数据,可得

(24)

由于光场所有模式之间没有关联,因此光场总的偏态信息为所有的It(ρF,s)相加,即

(25)

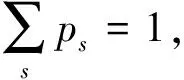
(26)

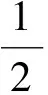
(27)

式(27)表明光场的偏态信息依赖于〈Sz〉.

二能级原子和光场偏态信息的演化特性如图1所示,其中图1(A)为Dicke模型,图1(B)为J-C模型.由图1(A)可见:在原子从激发态逐渐演化到最大混合态,最后演化到基态的过程中,原子信息经历了一个从1/2逐渐变小到零,又逐渐增大到1/2的过程,如图1(A)中实线所示;光场的偏态信息也经历一个类似过程,但当原子信息回到1/2时,光场信息达到最大值3/2,如图1(A)中虚线所示.当原子的偏态信息为零时,光场的偏态信息为初始值的1/2,即若将光场最小偏态信息对应的状态作为最大混合态的标准,则一个光子和真空场等概率混合时,不是最大混合态,这不同于二能级原子的最大混合态.此外,在原子从激发态跃迁到基态的过程中,光子的平均个数为一个随时间增加的函数,当原子处于基态时,光子个数应为1,比较光场的偏态信息曲线可见,光场的偏态信息依赖于光子的个数和光场的状态.随着时间的变化,原子最后稳定在基态,两个子系统的信息均未出现反弹现象.在自发辐射过程中,两个子系统之间不存在信息转移、存储和释放等现象,与电磁诱导光透明系统的结果不同[11].

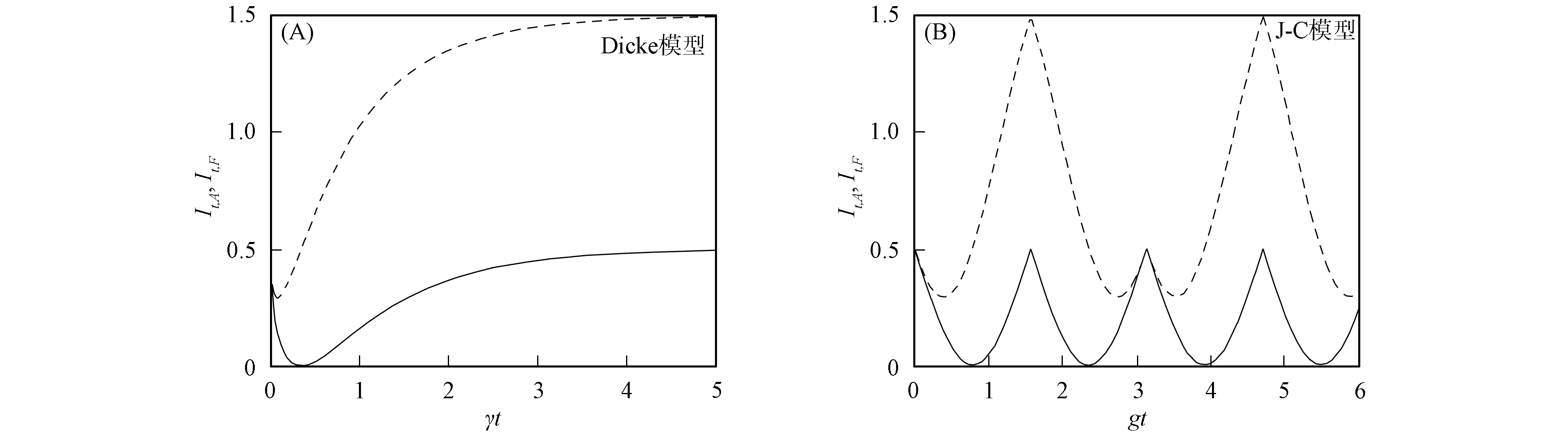
图1 原子偏态信息It,A(实线)和光场偏态信息It,F(虚线)的演化特性Fig.1 Evolutions of skew information of atom It,A (solid line)and that of optical field It,F (dashed line)

若二能级原子的自发辐射过程采用J-C模型处理[18],则可得相似的结论：

(28)

其中θ=gt,g表示光场和二能级原子的耦合常数.Sz的平均值为(cos2θ-sin2θ)/2,将式(28)分别化为式(21)和式(27).由图1(B)可见,二能级原子与光场的偏态信息呈周期性变化,但与Dicke模型所得结果不同.

综上,本文研究了单个二能级原子从激发态自发辐射到基态过程中原子和光场的偏态信息,通过分析可得如下结论：

1)二能级原子在激发态和基态具有相同的Wigner-Yanase偏态信息,在最大混合态时Wigner-Yanase偏态信息达到最小值零.

2)光场的Wigner-Yanase偏态信息依赖于光场的平均光子数和光场的状态;真空态|0〉和光子数态|1〉等概率混合时,偏态信息未达到最小值.

3)原子对光场的信息没有存储和释放功能.

[1] Bennett C H,Brassard G,Crépeau C,et al.Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels [J].Phys Rev Lett,1993,70(13):1895-1900.

[2] Bouwmeester D,PAN Jianwei,Mattle K,et al.Experimental Quantum Teleportation [J].Nature,1997,390:575-579.

[3] Wigner E P,Yanase M M.Information Contents of Distributions [J].Proc Natl Acad Sci USA,1963,49(6):910-918.

[4] LUO Shunlong,FU Shuangshuang,Choo H O.Quantifying Correlations via the Wigner-Yanase Skew Information [J].Phys Rev A,2012,85(3):032117.

[5] LUO Shunlong.Wigner-Yanase Skew Information vs Quantum Fisher Information [J].Proceedings of the American Mathematical Society,2004,132(3):885-890.

[6] LUO Shunlong.Wigner-Yanase Skew Information and Uncertainty Relations [J].Phys Rev Lett,2003,91(18):180403.

[7] LUO Shunlong.Heisenberg Uncertainty Relation for Mixed States [J].Phys Rev A,2005,72(4):042110.

[8] CHEN Zeqiang.Wigner-Yanase Skew Information as Tests for Quantum Entanglement [J].Phys Rev A,2005,71(5):052302.

[9] LIU Wanfang,YIN Xunchang,ZHANG Lihua.Storage of Maximal Wigner-Yanase Skew Information of Two-Qubit System Using Nonlinear Interactions with Decay [J].Int J Theor Phys,2011,50(11):3375-3384.

[10] SUN Honggui,LIU Wanfang,LI Chunjie.Maximal and Total Skew Information for a Two-Qubit System Using Nonlinear Interaction Models [J].Chin Phys B,2011,20(9):090301.

[11] 付静,刘万芳,赵玉杰.电磁诱导光透明过程中Wigner-Yanase偏态信息 [J].物理学报,2013,62(17):170302.(FU Jing,LIU Wanfang,ZHAO Yujie.Wigner-Yanase Skew Information of the System with the Electromagnetically Induced Transparency [J].Acta Phys Sin,2013,62(17):170302.)

[12] 宋明玉,吴耀德.微波驱动双模四能级单原子中连续变量纠缠的制备 [J].物理学报,2013,62(6):064207.(SONG Mingyu,WU Yaode.Generation of Continuous-Variable Entanglement in a Two-Mode Four-Level Single-Atom Driven by Microwave [J].Acta Phys Sin,2013,62(6):064207.)

[13] CAO Zhuoliang,ZHANG Lihua,YANG Ming.Concentration for Unknown Atomic Entangled States via Cavity Decay [J].Phys Rev A,2006,73(1):014303.

[14] DUAN Luming,GUO Guangcan.Scheme for Reducing Decoherence in Quantum Computer Memory by Transformation to the Coherence-Preserving States [J].Chin Phys Lett,1997,14(7):488-491.

[15] Poulsen U V,Mφlmer K.Squeezed Light from Spin-Squeezed Atoms [J].Phys Rev Lett,2001,87(12):123601.

[16] Davide G,Tommaso T,Gerardo A.Characterizing Nonclassical Correlations via Local Quantum Uncertainty [J].Phys Rev Lett,2013,110(24):240402.

[17] ZHONG Wei,SUN Zhe,MA Jian,et al.Fisher Information under Decoherence in Bloch Representation [J].Phys Rev A,2013,87(2):022337.

[18] Scully M O,Zubairy M S.Quantum Optics [M].Cambridge:Cambridge University Press,2000.

(责任编辑：王 健)

Wigner-YanaseSkewInformationintheProcessofSpontaneousEmissionbetweenTwoAtomicLevels

LIU Wanfang1,YIN Xunchang1,FU Jing2,LI Min3

(1.SchoolofPhysicsandElectricEngineering,AnqingTeachersCollege,Anqing246011,AnhuiProvince,China;2.TheCityCollegeofJilinJianzhuUniversity,Changchun130111,China;3.JimeiUniversityChengyiCollege,Xiamen351100,FujianProvince,China)

We investigated the changes of the Wigner-Yanase information in the processes of the spontaneous emission of a two-level atom system,and calculated the Wigner-Yanase information for the reduced density matrix of the atom and that for the quantum radiation respectively.Our investigations show that both of them depend on the expectation of 〈Sz〉.And the Wigner-Yanase information for the radiation field reach the maximum when the atom stays in the ground state.Additionally,the results also show that both the atom and the field will not simultaneously become the maximal mixed state.

two-level atom;spontaneous emission;Dicke mode;Wigner-Yanase skew information;mixed state

10.13413/j.cnki.jdxblxb.2015.03.36

2014-07-18.

刘万芳(1979—),男,汉族,硕士,副教授,从事量子信息的研究,E-mail:lwf2002251@126.com.通信作者:李 敏(1980—),女,汉族,硕士,讲师,从事量子信息的研究,E-mail:190930259@qq.com.

安徽省自然科学基金(批准号:1408085QA15)和福建省中青年教师教育科研基金(批准号:JB14219).

O431.2

：A

：1671-5489(2015)03-0542-05