应用首次积分法求解非线性波动方程

尹伟石,孟品超,李延忠

(1.长春理工大学 理学院,长春 130022；2.北华大学,吉林 吉林 132013)



研究简报

应用首次积分法求解非线性波动方程

尹伟石1,孟品超1,李延忠2

(1.长春理工大学 理学院,长春 130022；2.北华大学,吉林 吉林 132013)

利用首次积分法求解一类非线性波动方程的行波解,得到了行波解的精确表达式.数值算例表明,对于同类的双曲型发展方程,该方法仍然有效.

首次积分法；非线性波动方程；行波解

非线性偏微分方程(组)在流体动力学、等离子体物理学、光学、固态物理学和交通等领域应用广泛.由于描述问题的复杂性和非线性项的影响,求解解析解几乎是不可能的,因此求解非线偏微分方程(组)行波形式的精确解具有重要意义.随着孤波理论的发展,目前已报道一些方法求正解非线性偏微分方程的精确解,如逆散射转变[1]、双曲切-双曲正割法[2-3]、,齐次平衡法[4]、指数函数法[5]、(G/G′)展开法[6-7]和首次积分法[8]等.本文主要考虑应用首次积分法求解非线性波动方程精确形式的行波解,首次积分法的优势是整个迭代算法为纯代数运算,从而可借助符号计算软件进行求解.

1 算法简介

定理1(Division定理)[9]假设P(W,Z),Q(W,Z)是复数域C(W,Z)上的多项式,并且P(W,Z)在C(W,Z)上是不可约的.如果P(W,Z)=0的零点也为Q(W,Z)的零点,则在复数域C(W,Z)上存在一个多项式G(W,Z),使得Q(W,Z)=P(W,Z)G(W,Z).

首次积分法的基本思想是先将非线性偏微分方程通过行波变换转化为常微分方程,再对常微分方程进行适当变化转化为常微分方程组,进而求解非线性偏微分方程的精确解.步骤如下：

1)考虑一般非线性发展方程

(1)

2)使用行波变量ξ=x-ct对式(1)进行变换u(x,t)=U(ξ),得

(2)

3)假设引入新的变量u(x,t)=f(ξ),则式(2)可化为

(3)

其中f是假设由式(2)可得到的解析表达式,从而得到一个微分系统

(4)

其中F是由式(3)得到的关于Y的导数表达式;

4)先利用常微分方程定性理论与Division定理得到式(3)的一个首次积分,再代入方程(2)得到该方程的解,即得到式(1)的精确解.

2 首次积分法的应用

下面利用首次积分法求解非线性波动方程的精确解.考虑

(5)

其中:α>0;β,γ为实常数.运用变换u(x,t)=f(ξ),ξ=x-λt,可将式(5)转化成为常微分方程：

(6)

由式(4)可得

(7)

(8)

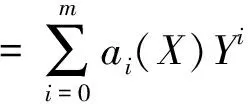
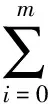
(9)

其中ai(X)(i=1,2,…,m)是关于X的多项式,且am(X)≠0.式(9)称为式(7)-(8)的首次积分.根据Division定理,存在一个多项式g(X)+h(X)Y,使得在域C[X,Y]内有

(10)

本文主要讨论m=1的情况.由式(10)可得

(11)

令式(11)两边关于Yi(i=0,1,2)的系数相等,可得

(12)

(13)

(14)

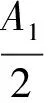
情形1)

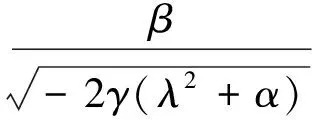
(15)

把式(15)代入式(9)有

(16)

比较式(16),(7)可得式(6)的精确解：

(17)

其中C1是常数.因此方程(5)的精确解可以写成

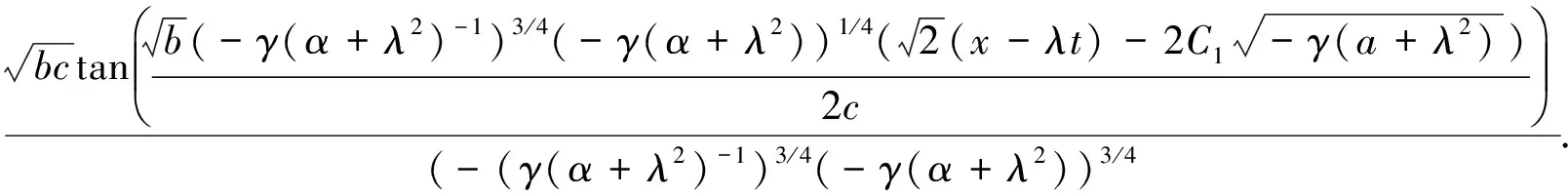
情形2)

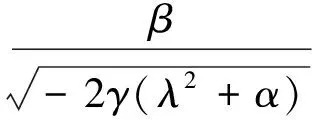
(18)

把式(18)代入式(9)有

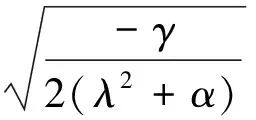
(19)

比较式(7),(19)可得式(6)的精确解：

其中C1是常数.从而可得方程(5)的解：

综上可见,首次积分法对于求该类非线性波动方程的精确解是一种可行有效的方法,因此,对类似的双曲型偏微分方程如非线性梁方程、非线性Schrödinger方程等也可以用该方法求其精确解.

[1] Malfliet W,Hereman W.The tanh Method.Ⅰ.Exact Solutions of Nonlinear Evolution and Wave Equations [J].Physica Scripta,1996,54(6):563-568.

[2] Wazwaz A M.The tanh Method for Travelling Wave Solutions of Nonlinear Equations [J].Appl Math Comput,2004,154(3):713-723.

[3] CHANG Jing,GAO Yixian,CAI Hua.Generalized Extended tanh-Function Method for Traveling Wave Solutions of Nonlinear Physical Equations [J].Commun Math Res,2014,30(1)：60-70.

[4] FAN Engui,ZHANG Hongqing.A Note on the Homogeneous Balance Method [J].Phys Lett A,1998,246(5):403-406.

[5] HE Jihuan,WU Xuhong.Exp-Function Method for Nonlinear Wave Equations [J].Chaos Solitons and Fractals,2006,30(3):700-708.

[6] WANG Mingliang,LI Xiangzheng,ZHANG Jinliang.The (G′/G)-Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics [J].Phys Lett A,2008,372(4):417-423.

[7] 常晶,刘丽环,高忆先,等.利用改进的(G′/G)函数法求解非线性发展方程的行波解 [J].吉林大学学报:理学版,2012,50(3):487-493.(CHANG Jing,LIU Lihuan,GAO Yixian,et al.Traveling Wave Solutions of Nonlinear Evolution Equations by Improved (G′/G)Method [J].Journal of Jilin University:Science Edition,2012,50(3):487-493.)

[8] Raslan K R.The First Integral Method for Solving Some Important Nonlinear Partial Differential Equations [J].Nonlinear Dynamics,2008,53(4):281-286.

[9] LU Bin.Division Theorem Combined with the Riccati Equation for Solving Some Nonlinear Schrödinger-Like Equations [J].Appl Math Comput,2012,219(4)：1686-1694.

(责任编辑：赵立芹)

ExactSolutionsforNonlinearWaveEquationsbyFirstIntegralMethod

YIN Weishi1,MENG Pinchao1,LI Yanzhong2

(1.CollegeofScience,ChangchunUniversityofScienceandTechnology,Changchun130022,China;2.BeihuaUniversity,Jilin132013,JilinProvince,China)

We used the first integral method to solve a class of nonlinear wave equations and obtained the exact form of traveling wave solutions.Furthermore,the validity and efficiency of this method were shown by numerical calculation of nonlinear wave equation,indicating that it can be applied to other hyperbolic evolution equations.

first integral method;nonlinear wave equation;traveling wave solutions

10.13413/j.cnki.jdxblxb.2015.03.19

2014-09-10.

尹伟石(1980—),男,汉族,博士研究生,讲师,从事数学物理反问题及数值计算的研究,E-mail:yinweishi@foxmail.com.通信作者：李延忠(1978—),男,汉族,博士,教授,从事最优化理论与计算方法的研究,E-mail:liyz.bh@gmail.com.

国家自然科学基金(批准号：51278221;51378076).

O175.14

：A

：1671-5489(2015)03-0454-03