不同选样方法设计暴雨重现期衔接关系探讨

黄国如，曾娇娇，张明珠，武传号，刘 浩

（1.华南理工大学土木与交通学院，广东广州510640；2.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640；3.广州市水务科学研究所，广东广州510220）

不同选样方法设计暴雨重现期衔接关系探讨

黄国如1，2，曾娇娇1，张明珠3，武传号1，刘 浩3

（1.华南理工大学土木与交通学院，广东广州510640；2.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640；3.广州市水务科学研究所，广东广州510220）

摘要:目前国内推行采用年最大值法进行短历时暴雨选样 ，为了解决年最大值法选样在小重现期（1 a ～5 a）内暴雨强度设计值明显偏小以及设计重现期的衔接问题，以广州市设计暴雨为例，采用不同频率分布模型对年最大值法及年多个样法进行频率分布适线 ，得到不同情形下的暴雨强度公式。结果表明，虽然不同频率分布模型对两种选样方法的衔接关系有较大影响，但转换的年最大值法可在一定程度上改进由年最大值选样引起的小重现期暴雨强度较小的问题 ，同时也可解决室外排水工程常用设计重现期统一问题。

关键词:暴雨强度公式；年最大值法；年多个样法；频率分布；重现期衔接

1　研究背景

暴雨选样是城市暴雨强度公式分析过程中最为基础和重要的工作，它对暴雨强度公式的推求及精度有着至关重要的影响。我国自20世纪60年代起开始采用年多个样法，并将该法列入《室外排水设计规范》中。由于年多个样法选样在理论和实际应用上存在的问题日益凸显，加之我国目前大多地区已具有40 a以上的自记雨量资料 ，具备采用年最大值法条件，故《室外排水设计规范》［1］（GB50014-2006）规定具有20 a以上自记雨量记录的地区，应采用年最大值法推求排水系统设计暴雨强度公式。然而，年最大值法选样会遗漏较大场次的暴雨，导致排水设计中常用的小重现期暴雨强度设计值偏小。考虑到推行年最大值选样后工程设计标准的连续性以及已建工程设计标准校核等设计重现期统一问题，有必要对两种选样方法的衔接关系进行深入探讨。

关于两种选样方法的衔接关系，国内已有学者做了相关研究 ，邓培德［2］采用数理统计方法推导得出年多个样法与年最大值选样之间的重现期衔接关系式，指出两种选样方法在理论上的衔接关系是概率关系 ，并且这种关系只有在资料年份较长且符合推理过程假设的条件下才为可靠；卢金锁等［3］以西安市暴雨资料为基础，将经重现期前、后转换的年最大值法与年多个样法的暴雨强度值进行比较，结果表明经重现期前、后转换的年最大值法的暴雨强度与年多个样法推求的暴雨强度接近，提出转换的年最大值法推求的暴雨强度公式可替代年多个样法推求的暴雨强度公式；周玉文等［4］采用年多个样法与年最大值法对北京市连续68 a雨量资料的研究表明，两种选样方法的重现期并没有确定的定量关系，目前主要根据实际样本资料和分布结果，给出两种选样方法重现期的初步对应关系。邵卫云［5］基于降雨资料系列的水文特性，根据雨强相等的原则，推导出暴雨选样方法之间的频率转换关系，并探讨了降雨历时与年均选样个数对转换关系的影响。就国内的研究现状而言，目前仍缺乏被普遍认可的年最大值法与年多个样法的重现期对应转换关系。鉴于此，本文基于广州市连续30 a短历时暴雨资料，对两种选样方法采用不同频率分布适线以推求其暴雨强度公式，探寻两者之间的衔接关系。

2　两种选样方法对比

年最大值法选样是按不同历时每年选取一个最大值，这样的选样方法独立性强，特别是合理地考虑了气象学的一年循环周期，其概率意义是一年发生一次的频率，按极值理论，当资料年份很长时地近似于全部水文资料的计算值，理论上严密。但这种选样方法会遗漏一些较大雨样，使得小重现期部分的降雨强度明显偏小。其经验重现期计算公式为［6］:

式中:TM为年最大值法重现期（a）；N为降雨资料年数；m为样本系列值由大到小排列的序位。

年多个样法选样是按不同历时每年选取最大6 个 ～8个暴雨雨样，不论年次按从大到小统一排序后，再取资料年数的3倍 ～4倍的最大雨样作为统计基础资料，这种方法解决了暴雨雨样标准的不确定性问题 ，同时弥补了各地暴雨资料年份不足的缺陷，避免遗漏较大的雨样，在小重现期（0.25 a～5 a）部分，能比较真实地反映暴雨的统计规律，但该法存在资料收集与统计较为困难等问题 ，且所需费用较大。其经验重现期计算公式为［6］:

式中:TE为年多个样法重现期（a）；k为每年平均取样个数。

根据已有研究，年最大值法与年多个样法选样所得的经验重现期含义不同，基于数理统计理论，两者符合如下的概率关系［2］:

式（3）所示的两种选样样本经验重现期对应关系如表1所示。

表1　年多个样法重现期TE与年最大值法重现期TM的概率对应关系

3　实例研究

采用广州市连续30 a（1984年—2013年）自记雨量计雨量资料，按照规范要求分9个历时（5 min、10 min、15 min、20 min、30 min、45 min、60 min、90 min、120 min）选样。按年最大值法选样要求，每年选取各相应历时的年最大降雨量，不论年次按从大到小统一排序 ，得到各个历时30个雨样的暴雨资料，计算统计各个历时的暴雨强度，利用式（1）计算其对应的经验重现期。按年多个样法选样要求，每年选取各相应历时的前8大降雨量，不论年次按雨量从大到小统一排序，再取资料年数4倍的最大雨样作为统计的基础资料，将最终得到的9个历时的雨量资料除以其相应历时，统计得到各个历时的暴雨强度，利用式（2）计算其对应的经验重现期。

3.1样本比较

根据排序后的年多个样法与年最大值法选样样本，采用海森概率格纸坐标以重现期为横坐标 ，雨强为纵坐标 ，绘制不同历时下两种选样样本点的雨强与重现期关系图，本文以10 min、30 min、60 min、90 min为例，结果见图1。

图1　年多个样法与年最大值法样本各历时雨强-重现期关系对比图

由图1可知，在小重现期1 a～5 a内，年最大值法所选雨样的降雨强度明显小于年多个样法所选雨样的降雨强度，但重现期在5 a以上时，两者差异较小，这主要是因为年最大值法选样忽略了大雨年份中较大的雨样，而年多个样法选样不会遗漏较大雨样，所以年多个样法在小重现期部分能较真实地反映城市排水设计常用重现期范围内的雨样统计规律。由于我国现行排水规范常用的设计重现期为1 a～5 a，故探寻两种选样方法的衔接关系对于解决年最大值法选样在小重现期部分设计降雨强度值偏小有较大意义。

对年多个样法与年最大值法样本进行统计对比，分别对比两种选样样本在表1所示各对应的经验重现期下不同历时的降雨强度值，对比成果如图2。由图2可见，虽然两种选样方法各对应重现期的暴雨强度值有一定偏差，但总体而言，各对应重现期的暴雨强度值相当 ，可见年多个样法与年最大值法样本的经验重现期服从式（3）所示的概率关系。

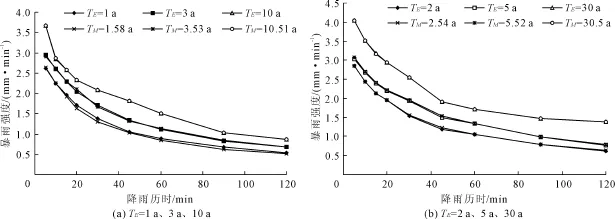
图2　年多个样法与年最大值法选样样本对应重现期暴雨强度对比图

3.2频率分布适线及选择

根据自记雨量资料推求暴雨强度的频率分布规律是确定设计暴雨的依据，它决定着所用频率-强度-历时关系的可靠性。然而选择何种理论或经验频率分布模型进行频率适线，目前尚无统一定论［7-11］。

对于指数分布，各历时雨强 ip与重现期T的关系为［10］:

参数 a、b由矩法求得:

式中:xj为排位第j项的雨强实测值；n为雨强序列总数。

对于耿贝尔分布，各历时雨强 ip与重现期T的关系为［11］:

由最小二乘法求得参数 u、v:

式中:Kj为排位第j项的Tj计算值。

对于P-Ⅲ型分布［12］，可以采用适线法根据实测系列得出三个统计参数（¯x—均值；Cv—离差系数；Cs—偏差系数），在频率计算时，先由已知Cs可通过查表得出不同频率 P的离均系数Φp值，然后将 Φp及已知的¯x、Cv代入式（9），即可求出对应于频率 P的暴雨强度值ip。

根据前人研究成果，在上述样本的基础上，对年多个样法和年最大值法分别采用指数分布、耿贝尔分布和P-Ⅲ型分布模型适线，适线结果及误差见表2。

由表2的适线结果可知，对于年多个样法，耿贝尔分布模型适线误差较大，绝对均方差及相对均方差均超过0.05，不宜选取，可选取指数分布和P-Ⅲ型分布的适线结果统计雨强-历时-重现期关系数据表；对于年最大值法，指数分布模型适线误差较大，绝对均方差及相对均方差均超过0.05，不宜选取，可选取耿贝尔分布和P-Ⅲ型分布的适线结果统计雨强-历时-重现期关系数据表。

表2　不同选样方法频率适线结果及误差

3.3 暴雨强度公式参数拟合及分析

根据两种选样方法的雨强-历时-重现期关系数据表 ，采用麦夸特优化算法［13］拟合得到暴雨强度公式参数。同时，根据式（3）将年最大值法的雨强-历时-重现期数据表中的重现期 TM转换为TE，进而拟合暴雨强度公式参数（即转换的年最大值法）。根据我国常用暴雨强度公式（式（10））和《室外排水设计规范》［1］（GB50014-2006）重现期选择要求，拟合所得各暴雨强度公式参数及拟合误差见表3。

式中:i为暴雨强度（mm/min）；t为降雨历时（min）；T为重现期（a）；A1、C、b、n为地区参数。

由表3可见，同一选样方法，经不同频率分布模型适线后所得的暴雨强度公式有一定差别。从三种方法的拟合误差可以看出，转换的年最大值法暴雨强度公式拟合值与实测值的绝对均方差比年最大值法小，接近于年多个样法。对比表2和表3可知，两种选样方法采用P-Ⅲ型分布适线所得的绝对均方差均为最小，但所得暴雨强度公式拟合值与实测值的绝对均方差未达到最小 ，由此可见并不是频率分布适线绝对均方差越小拟合所得的暴雨强度公式精度越高，故频率分布适线不宜仅以绝对误差最小为择优原则。

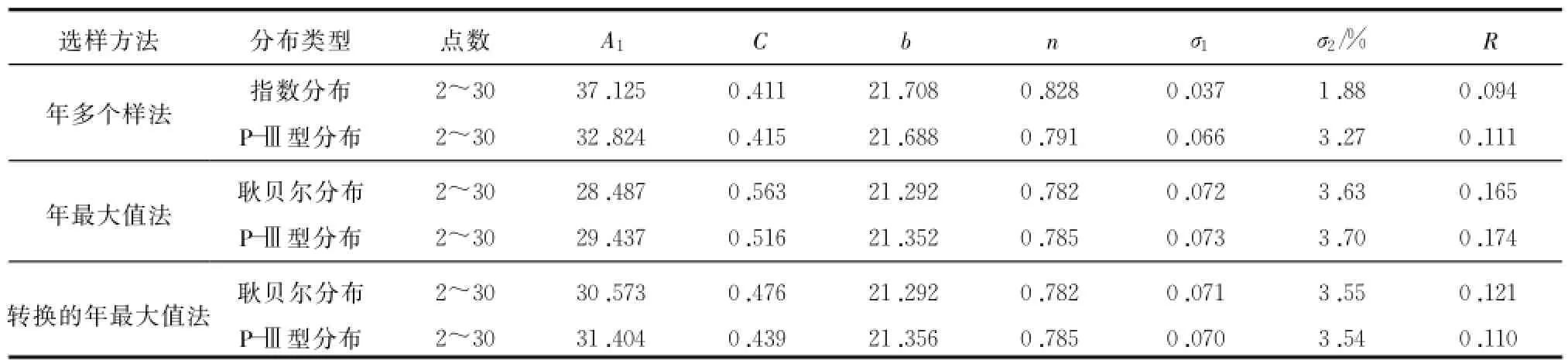
表3　不同选样方法暴雨强度公式参数及误差

利用表3暴雨强度公式参数，计算特定短历时暴雨下年多个样法与年最大值法暴雨强度公式的重现期对应关系，得出两种选样方法在不同频率分布适线后的两组重现期对应关系（表4和表5）。

表4　年多个样法（指数分布）与年最大值法（耿贝尔分布）暴雨强度公式的重现期对应关系

由表4、表5可知，年多个样法与年最大值法暴雨强度公式的重现期对应关系不仅随降雨历时变化，而且与频率分布模型的选取密切相关。从两种选样方法的重现期对应关系来看 ，两种选样方法经频率分布适线后拟合所得暴雨强度公式并不服从式（3）所示的概率关系。

表5　年多个样法（P-Ⅲ分布）与年最大值法（P-Ⅲ分布）暴雨强度公式的重现期对应关系

为了进一步研究两种选样方法在式（3）所示概率关系下的暴雨强度值对比关系，根据表2推导所得的年多个样法、年最大值法及转换的年最大值法暴雨强度公式，分别计算其在不同重现期不同降雨历时下的暴雨强度值，结果如图3和图4。

图3　耿贝尔、指数分布适线方法暴雨强度计算值对比图

图4　P-Ⅲ型适线方法暴雨强度计算值对比图

由图3可以看出，年多个样法与转换的年最大值法的暴雨强度只在小于5 a一遇的小重现期下接近，在10 a以上的大重现期下，年多个样法暴雨强度最小 ，年最大值法与转换的年最大值法均大于年多个样法。

由图4可以看出，年多个样法与转换的年最大值法的暴雨强度计算值曲线几乎完全重合，且在10 a以下的重现期年多个样法均大于年最大值法的暴雨强度计算值，当重现期大于10 a一遇时，三者计算所得的暴雨强度值曲线逐渐重合。

综合分析可知，当年最大值法与年多个样法均采用P-Ⅲ型分布模型适线时，式（3）可作为两种选样方法所得暴雨强度公式的重现期衔接转换关系；当年最大值法与年多个样法分别选用耿贝尔分布与指数分布进行频率分布适线时，式（3）所示的转换关系只在重现期小于5 a一遇时满足两种选样方法重现期的衔接转换关系，其原因在于式（3）是两种选样方法理论上的概率关系而不是函数关系 ，只有在资料年份较长且符合推理过程假设的条件下才适用，而且两种选样的频率分布适线及暴雨参数拟合过程均存在一定误差。虽然不同的频率分布模型适线对两种不同选样方法所得暴雨强度公式的重现期衔接关系有着较大的影响，但经转换后的年最大值可在一定程度上改进由年最大值选样引起的小重现期暴雨强度较小的问题 ，同时也可保留大重现期暴雨强度较大的特点。

4　结 论

本文分别采用年最大值法与年多个样法对广州市连续30 a自记雨量资料进行一系列分析，得到的主要结论如下:

（1）年多个样法与年最大值法选样样本在表1所示对应重现期下的暴雨强度值相当，进一步验证了两种选样样本的经验重现期概率关系的正确性。

（2）两种不同选样方法经频率分布适线拟合所得暴雨强度公式的重现期对应关系不仅随降雨历时的改变而改变，也与适线的频率分布模型有关，其重现期对应关系随适线的频率分布模型不同呈现较大的差异 ，故不能简单地以两种不同选样方法的重现期对应关系来概化其衔接关系。

（3）虽然两种选样方法拟合所得暴雨强度公式的重现期不再服从式（3）所示的概率关系，但经该概率关系转换的年最大值可以在一定程度上改进由年最大值选样引起的小重现期暴雨强度较小的缺点，解决我国室外排水设计在推行年最大值选样后工程设计标准的连续性以及已建工程设计标准校核等设计常用重现期的统一问题。

参考文献:

［1］ 中华人民共和国建设部，中华人民共和国国家质量监督检验检疫总局.GB50014-2006.室外排水设计规范［S］.北京:中国计划出版社，2006.

［2］ 邓培德.城市暴雨两种选样方法的概率关系与应用评述［J］.给水排水，2006，32（6）:39-42.

［3］ 卢金锁，程 云，王社平 ，等.暴雨强度公式推求过程简化研究［C］//Proceedings of the 3rd International Conference on Computational Intelligence and Industrial Application（PACIIA）.中国，武汉 ，2010:249-252.

［4］ 周玉文，翁窈瑶，张晓昕，等.应用年最大值法推求城市暴雨强度公式的研究［J］.给水排水，2011，37（10）:40-44.

［5］ 邵卫云 .基于水文特性的暴雨选样方法的频率转换［J］.浙江大学学报:工学版，2010，44（8）:1597-1603.

［6］ 郝树棠.一年多次法和超定量法选样重现期的计算问题［J］.中国给水排水，1989，5（5）:40-42.

［7］ 邓培德，韦鹤平，俞庭康，等.城市暴雨公式统计方法的研究［J］.同济大学学报:自然科学版，1985，（1），17-29.

［8］ 邓培德.城市暴雨公式统计中若干问题［J］.中国给水排水，1992，8（3）:45-48.

［9］ 夏宗尧.评《城市暴雨公式统计中若干问题》［J］.中国给水排水，1997，13（5）:22-24.

［10］ 朱颖元，米伟亚.城市短历时暴雨的指数分布及参数估计［J］.福州大学学报:自然科学版，2005，33（3）:285-288.

［11］ 王俊萍.推求绵阳市暴雨强度公式的问题研究［D］.西安:西安建筑科技大学，2007.

［12］ 杨智硕，陈明霞.福建省城市短历时暴雨P-Ⅲ分布统计参数分布规律研究［J］.湖南工业大学学报 ，2010，24（5）:64-66.

［13］ 任伯帜，许仕荣 .基于Marqardt—Hartley法及其在求解城市暴雨强度公式参数中的应用研究［J］.湖南大学学报:自然科学版，2002，29（3）:96-100.

中图分类号:P333.2

文献标识码:A

文章编号:1672—1144（2015）01—0030—06

DOI:10.3969/j.issn.1672-1144.2015.01.007

收稿日期 :2014-10-21修稿日期:2014-11-27

基金项目 :广州市水务科技项目（GZSW-201309）；水利部公益性行业科研专项经费项目（201301093，201401048）；华南理工大学亚热带建筑科学国家重点实验室自主研究课题项目（2014ZC09）

作者简介 :黄国如（1969—），男，江苏南京人，教授 ，博导 ，主要从事水文水资源教学与科研工作。E-mail:huanggr@scut.edu.cn

Study on Convergence of Rainstorm Return Periods and Different Sampling Methods

HUANG Guo-ru1，2，ZENG Jiao-jiao1，ZHANG Ming-zhu3，WU Chuan-hao1，LIU Hao3
（1.School of Civil Engineering and Transportation，South China University of Technology，Guangzhou，Guangdong 510640，China；2.State Key Laboratory of Subtropical Building Science，South China University of Technology，Guangzhou，Guangdong 510640，China；3.Guangzhou Hydraulic Research Institute，Guangzhou，Guangdong 510220，China）

Abstract:The annual maximum method is recommended in short duration storm sampling in our country，which brings the problem that the storm intensity designed using this method is significantly smaller in the small return period（1 a～5 a），and the convergence of the designed return periods are not sound.In order to solve this problem，different frequency distribution model were adopted to fit the annual maximum series（AMS）and the annual multi-peak series（AMPS）in the rainstorm designing of Guangzhou.And then the storm intensity formula under various circumstances was obtained. The results indicate that different frequency distribution models have great impacts on the convergence between the two sampling methods.However the improved annual maximum method can improve the problem of small storm intensity in small return period to some extent，as well as unifies the return periods which are commonly used in the designing of outdoor drainage works.

Keywords:storm intensity formula；annual maximum method；annual multi-sampling method；frequency distribution；convergence of return periods