岩土预应力锚固作用三维数值模拟的等效力法
徐 祥,戴自航,2
(1.福州大学岩土工程研究所,福建福州350108;2.卧龙岗大学土木、采矿与环境工程学院,澳大利亚新南威尔士洲2522)
岩土预应力锚固作用三维数值模拟的等效力法
徐 祥1,戴自航1,2
(1.福州大学岩土工程研究所,福建福州350108;2.卧龙岗大学土木、采矿与环境工程学院,澳大利亚新南威尔士洲2522)
摘要:预应力锚索(杆)加固岩土是一典型的岩土与结构的空间相互作用问题。为可靠模拟这种结构与岩土的相互作用,提出了与工程中预应力施加和锁定工况相符的三维数值模拟分析等效力法。在ABAQUS有限元软件平台上,首先将该方法运用在单根预应力锚索的数值模拟试验,并与等效降温法和等效应变法进行对比分析,结果表明了该方法的优越性 ,此外,也分析了锚固段锚索轴力衰减速率与锚固体刚度有关,且与理论认识一致。然后,将等效力法应用在一实际预应力锚索加固边坡工程三维数值模拟中,分析了预应力锚索对加固边坡内部应力分布、边坡稳定性及锚索轴力分布的影响,表明该方法能可靠地应用于分析预应力锚索加固岩土的效果及锚索自身内力。
关键词:预应力锚索;相互作用;等效力法;锚索轴力;边坡加固;稳定系数
预应力锚索(杆)与所有传统的非预应力支护结构(非预应力锚索、抗滑桩、土钉、挡土墙等)相比能提供一种强有力的“主动”支护。因此预应力锚索被广泛应用在边坡工程,基坑工程,坝体加固工程,抗浮工程等领域,它具有以下优点[1]:(1)安装后能及时提供支护抗力即主动防护,使岩土体处于三轴应力状态;(2)按一定密度布置预应力锚杆后能在地层内形成压缩区,有利于地层稳定;(3)能明显地提高潜在滑移面或岩石软弱结构面的抗剪强度;(4)使地层与结构物抵抗变形的能力增强等。因此自1934年全球首次使用预应力锚杆来保持加高后的坝体的稳定后,国内外学者对预应力锚杆做了大量的理论解析[2-4]、模型及现场试验[5-8]、数值模拟[8-18]等工作。例如,文献[3]用三参数的高斯曲线来描述不同工程类型的锚索、锚杆的锚固段剪应力分布曲线;文献[5]根据室内模型试验分析了锚索长度及预应力值大小对块状岩体加固效果的影响;文献[6]针对花岗岩类土质边坡现场测试,详细研究了锚固力在类土质边坡中的传递规律及锚索各段的拉力分布规律等;文献[8]以一深基坑开挖支护为例,分别对普通预应力锚杆、非预应力锚杆和全长黏结型预应力锚杆进行数值模拟并做了对比分析研究;文献[9]运用快速拉格朗日差分法模拟深基坑中单根预应力锚杆的加固作用机理,分析各个参数对锚杆拉拔力的影响。
在预应力锚索数值模拟中,预应力的施加方法有三种,即等效降温法(Equivalent Lowering Temperature),等效应变法(Equivalent Strain)和等效力法(E-quivalent Force)。但常用的是前两者,后者虽然在某些文献[17-18]中有所提及,但并未有关该模拟方法详细的报道。此外,虽然文献[9,12,14]均做了简单模型的锚索预应力施加数值模拟,但它们着重考虑的是施加拉力过程,而对锚索锁定后其轴力分布情况未有述及,对锚固体与周围岩土体的接触相互作用的考虑或有欠缺。因此,本文构思了与工程中预应力施加与锁定工况相符的三维数值模拟分析的等效力法,采用ABAQUS有限元程序,首先进行了单根预应力锚索的数值模拟试验,然后,介绍了该方法在预应力锚索加固边坡的三维数值模拟中的应用情况,包括锚索锁定后锚索轴力的分布规律。
1 单根预应力锚索的数值模拟试验
1.1模型简介
完整的预应力锚索由锚头、自由段、锚固段三部分组成。本模型(图1)为了更真实反映现场拉拔试验,在锚头外围增加一锚垫片,如图1(a)所示。数值模型边界为直径6 m、高11 m的圆柱体,上层为5 m厚土体,下层为6 m厚岩体;锚头为直径0.16 m、高0.3 m的圆柱体;锚垫板为内径0.16 m,外径0.4 m的圆环;锚索长11 m,直径 D=0.03 m,锚固段直径0.16 m,长5 m,自由段长5 m。边界条件设置:模型上端面是自由面,模型的侧面施加X和Y轴方向的位移约束,底部施加三向位移约束。土体按摩尔-库仑理想弹塑性(以下简称M-C)材料考虑,因拟施加预应力不大,其他材料均在弹性阶段工作,故按均质线弹性材料考虑。具体材料属性取值如表1所示。约束条件设置:锚索与锚固体和锚头为嵌入约束,锚垫片与土体之间设置tie约束,锚固体与周围岩体为库仑摩擦接触,摩擦系数为0.6。图1(b)为模型的有限元网格划分,岩土体和锚固体采用C3D4三维实体单元划分,锚索按梁单元划分,嵌入锚固段灌浆体中。

图1 有限元分析模型及其网格划分
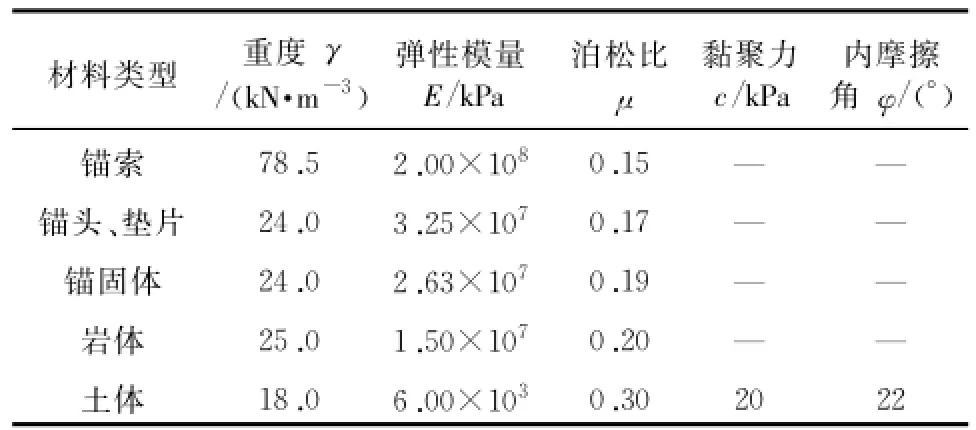
表1 模型材料力学参数
1.2计算结果分析
1.2.1 不同施加预应力方法所得结果对比分析
传统的等效降温法通过设置温度应变系数,在给定的温度变化下获得给定的应变,从而产生想要达到的预应力加载效果,所需给定的温度由公式(1)计算得到:

其中:Δ T为给定的温度变化;σ为所达到的锚索预应力(kPa);α为锚索线膨胀系数;取 α=1.0× 10-5/℃;E为锚索弹性模量(kPa)。
对于预应力产生的应变,等效应变法通过位移约束的方法加载,使结构中产生与预应力加载相当的应变。
本文提出的等效力法是使用能够产生同样大小预应力的等效集中力施加在锚头外露的锚索上,同时同值的力按面力施加在锚垫板上,即相当于锚索张拉时千斤顶的反力作用在锚垫板上。
现假设锚索施加100 kN的预应力,第一种方法所需的温度改变量通过公式(1)计算为 ΔΤ= -70.77℃;第二种施加的等效位移计算为 Ueq= 4.03 mm;第三种方法与现场施加预应力一致,图2为现场采用千斤顶施加预应力示意图,即对锚索施加拉力,同时对垫片施加等值的压力,等施加到预定的拉力值后,用锚垫片锚定锚索,阻止锚索在预应力值作用下收缩释放预应力 ,计算结果如图3所示。

图2 现场锚索预应力的施加
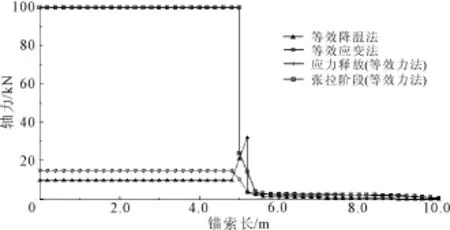
图3 锚索轴力(F1)分布
从图中可知只有等效力法达到预期目标,自由段的轴力 F1在张拉阶段为100 kN,释放拉力锚定后轴力 F1=99.89 kN;等效降温法和等效应变法并没有达到预期目标,自由段的轴力分别为9.74 kN 和14.89 kN,这是由于这两种方法施加预应力后,在预应力作用下引起锚头和垫片产生向土体中的位移,这就导致了锚索收缩,引起预应力损失,而要达到设计预拉力必需试算施加比理论上大得多的降温和应变 ,如降温Δ T=-1 400℃和施加等效位移 Ueq=230 mm。而等效力法在张拉阶段对垫片已施加等值的反向压力,垫片在该阶段位移已产生 ,在拉力释放阶段垫片不再产生向土体中的位移 ,故锚索自由段基本没有收缩,预应力基本没有损失,可见等效力法要优于常用的等效降温法和等效应变法。另外等效降温法的自由段与锚头和锚固段交界处的轴力明显大于自由段处的轴力 ,这是由于这两处分别受锚头与锚索、锚固段与锚索双向作用力,导致应力集中。
1.2.2 锚固体弹性模量对锚索轴力分布的影响
文献[4]从理论上得到:比值 Gs/Ea愈大,锚索轴力在锚固顶端衰减愈快,摩阻力在锚固顶端的分布就愈集中;反之,比值愈小,轴力沿锚固段衰减愈缓,摩阻力分布就愈均匀,其中 Gs为锚固体与锚固层界面的剪切模量,Ea为锚固段等效弹性模量。图4为有限元计算结果示意图,与理论推导的结论相符。其中算例-1、算例-2、算例-3和算例-4锚固体弹性模量 Ea分别为1.315×107kPa、2.63×107kPa、5.26×107kPa和1.052×108kPa。

图4 锚固段轴力分布与其弹性模量的关系曲线
1.2.3 岩土体中位移和应力分布特征
图5(a)、图5(b)分别显示在自由段下部及锚垫片外围土体产生向上位移且呈对称分布 ,这是由于这两部分土体分别受锚固段和垫片挤压所致。
图6所示为岩土体中竖直方向上的应力分布。在锚头下方形成了一个压应力锥;在锚固段起始端和锚垫片外围土体形成了拉应力区域,前者是由于土体被挤压向上导致土体受剪而产生拉应力;后者是由于锚固段受拉向上,锚固段和土体之间的摩擦力使土体受拉。
2 预应力锚索加固边坡数值模拟分析
2.1工程概况及建模
图7所示为贵州某高速公路边坡工程。该边坡表层为坡积土,下覆残积土,再下面一层是微风化岩。为保证高速公路的安全必须进行加固处理,现场采用预应力锚索进行加固,传力板尺寸为0.45 m ×0.45 m,间距1.2 m。

图5 模型Z 轴方向位移分布

图6 岩土体Z 轴方向应力分布

图7 预应力锚索加固边坡
图8为以该边坡工程为背景建立的二维模型(预应力锚索设置前),坡高15 m,坡角35°,土体和岩体均按M-C材料考虑,天然状态下该边坡的具体力学参数取值见表2。边界条件设置为:边坡左右两侧施加X轴方向的位移约束,底部则施加X、Y二方向的位移约束。现采用有限元强度折减法,按塑性区临界贯通判别标准,计算得到该边坡的稳定系数 FS≈1.0,由此可知该边坡处于临界稳定状态。图9为该边坡临界状态下等效塑性应变等值云图,从图9中可知潜在滑动面位于坡积土内,部分沿坡、残积土分界面,为下文确定锚固段长度提供依据。

图8 二维边坡模型

表2 模型材料力学参数
图9 临界状态下等效塑性应变等值云图
图10是在图8所示二维模型的基础上建立的三维预应力锚索加固模型,该模型宽度取实际边坡锚索间距1.2 m,垫片与实际边坡传力板大小一致。该模型的锚索与简单模型结构一致(图1(a)所示),锚固段长7 m,自由段长6.5 m,锚索截面直径 D= 0.04 m(由7根直径为15.2 mm钢绞线等面积得到),另外锚垫片和锚固体的材料属性与锚头的材料属性取为一致,具体数值见表2。边界条件设置为:边坡左右侧边界施加X轴方向的位移约束,边坡前后两侧施加Y轴方向的位移约束,底部则施加三方向的位移约束,坡顶、坡面及坡脚平面为自由表面。

图10 预应力锚索加固边坡的三维模型
图11 预应力锚索加固边坡三维有限元网格划分
2.2预应力锚索加固对边坡内部应力的影响
本模型数值模拟有两种施加预应力顺序,方案1即首先施加锚索1预应力,后施加锚索2预应力;方案2与方案1施加预应力顺序相反。
图12和图13分别为加固前后土体中竖向应力等值云图,由图可知由于锚索预应力的作用 ,被加固的土体竖向应力 S33增大,则土体之间的摩擦力也即增大(或者预应力的施加挤压土体,使土体的抗滑能力增大),从而使边坡的稳定性得以提高。特别指出在图13中处于锚固段区域且在边坡土分层处土体出现拉应力,与上文单根预应力锚索揭示的情况类似,也是由锚固段与土体之间摩擦力引起土体受拉所致。

图12 加固前 Z轴方向应力等值云图
2.3预应力大小对边坡稳定性的影响
为探讨锚索预应力大小对边坡稳定性的影响,笔者模拟计算了5种不同预应力工况下的边坡的稳定系数 Fs,如表3所示。可见边坡的稳定系数随预应力的增大而增大,但增幅总体上变缓。这是由于当预应力增大到一定值后,对位移控制效果已不明显,故安全系数增加幅度减小,甚至不变,这与预应力锚杆应用于控制基坑位移场的研究结论一致[10]。
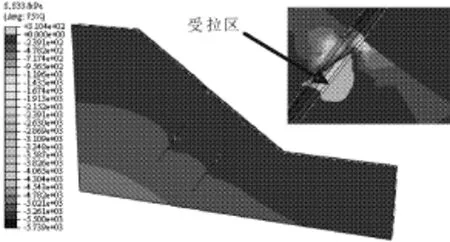
图13 加固后Z轴方向应力等值云图

表3 稳定系数 Fs计算结果
2.4锚索轴力分布分析
图14为按有限元强度折减至临界稳定状态时锚索轴力(F1)沿其长度分布,图中方案1-1表示锚索1按方案1所计算所得的轴力分布,其余同理。从图中可知:(1)两种方案锚索轴力分布一致,在强度折减阶段均产生预应力损失,这是由于土体强度指标降低 ,土体产生变形和锚头和垫片在预应力作用下产生向土体内位移,引起锚索收缩;(2)在自由段,两种方案锚索1的轴力比锚索2略大,而在锚固段则相反 ,这是由于边坡土体与锚索之间的相对位移引起的 ,这两者之间的相对位移边坡上部较边坡下部小,故而边坡上部锚索1自由段预应力损失较边坡下部锚索2小;由于锚索2的锚固段较锚索1的所受土压力大,在相同拉力作用下前者的位移较后者小,故锚索2锚固段的轴力较锚索1的轴力大;(3)锚固段轴力并非均匀分布,也并非由锚固段端部沿长度轴力值逐渐减小。在残积土中锚固段的锚索轴力逐渐减小,在微风化岩中轴力则先增大,达到一峰值后再逐渐减小。这可能是由于锚固段跨土层和岩层分布,锚固段与土体和岩体的剪切模量比不同引起的;(4)ABAQUS有限元软件中,数值为正表示拉力,负值表示受压。锚索1轴力在残积土与微风化岩分界面处减小至最小,其轴力为-21.11 kN。因此锚索在此处处于受压状态。这可能是由于残积土向下滑动,而微风化岩相对来说是静止不动的,导致锚固段弯曲,致使锚索受压。
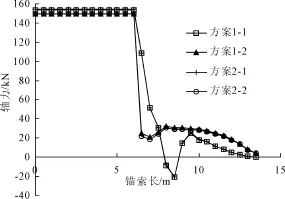
图14 临界稳定状态下锚索轴力(F1)分布
图15为边坡采用方案2锚固段锚索2轴力分布情况 ,这两条曲线分别表示的是锚定拉力释放状态(状态-1)和位移出现拐点时(状态-2)。这两种状态锚索轴力均首先从端部减小,之后再增大到一个较小峰值后,再逐渐减小,甚至趋于为零,而且大体上后者比前者锚索轴力分布均匀。另外,前者在锚固段前1.5 m锚索轴力大于后者锚索轴力,剩余长度(基本处于岩体中)则是后者的轴力大于前者。这可能是边坡经过强度折减,发生水平位移U1,锚索逐渐发挥出加固土体的作用,致使土体及锚索应力重新分布,处在岩体中的锚固段在这时刻已基本不再发生位移,但土体仍有向下滑动的位移,故对锚索有拉力作用,引起锚固段锚索轴力变大。

图15 锚固段锚索轴力分布
3 结 论
(1)采用等效力法施加预应力能真实的反映现场施加预应力过程,且从计算结果看,明显比等效降温法和等效应变法施加预应力效果好。
(2)理论上锚固段轴力的衰减速度与锚固体弹性模量有关,锚固体弹性模量越大,衰减越慢,反之越快,本文有限元计算结果与理论推导较为符合。
(3)由于锚固段跨土层和岩层分布,进行强度折减后,表层坡积土滑动,残积土相对坡积土具有滑动趋势,而岩层是稳定的,故导致锚固段在残积土和岩层中均受拉,但方向相反,导致:①在残积土中的锚固段锚索轴力减小,在岩层中锚固段锚索轴力先增大到一峰值,又逐渐减小,甚至趋于零;②在位移拐点时刻较锚定状态,岩层中锚固段的锚索轴力前者比后者大。
(4)锚固段在残积土和岩土分界面处,由于残积土向下滑动,而微风化岩相对来说是静止不动的,导致锚固段弯曲,使得该处锚索受压,出现压应力。
(5)边坡的稳定系数随锚索预应力的增大而增大,但总体上增幅逐渐减小,若施加预应力过大,则可能导致锚头部位土体发生局部破坏,故在施加预应力之前应验证锚头处土体承载力是否满足要求。不宜仅依靠增加单根锚索预应力大小来提高边坡的稳定安全系数。
参考文献:
[1] 程良奎,李象范.岩土锚固・土钉・喷射混凝土——原理、设计与应用[M].北京:中国建筑工业出版社 ,2008: 2-3.
[2] XIAO Shu-jun,CHEN Chang-fu.Mechanical mechanism analysis of tension type anchor based on shear displacement method[J].Journal of Central South University of Technology,2008,15(1):106-111.
[3] 蒋忠信.拉力型锚索锚固段剪应力分布的高斯曲线模式[J].岩土工程学报 ,2001,23(6):696-699.
[4] 张季如,唐保付.锚杆荷载传递机理分析的双曲函数模型[J].岩土工程学报 ,2002,24(2):188-192.
[5] 陈安敏,曹金刚.预应力锚索的长度与预应力值对其加固效果的影响[J].岩石力学与工程学报,2002,21(6): 848-852.
[6] 刘涌江,杨 静.预应力锚索加固花岗岩类土质高边坡的现场测试研究[J].岩石力学与工程学报,2011,30(增1):2924-2930.
[7] 韩 侃,李登科,吴冠仲.预应力锚索锚固力拉拔试验分析[J].岩土工程学报 ,2011,33(增1):385-387.
[8] 廖小平,王 浩,安孟康,等.全长黏结性预应力锚杆的数值分析与现场测试[J].岩石力学与工程学报,2006, 25(增2):415-420.
[9] 郑卫锋,贾金青.拉格朗日差分法的预应力锚杆数值模拟与应用[J].地下空间与工程学报,2009,5(6):1293-1297.
[10] 贾金青,郑卫锋 .预应力锚杆柔性支护法的研究与应用[J].岩土工程学报,2005,27(11):1257-1261.
[11] 贾金青,郑卫锋,陈国周.预应力锚杆柔性支护技术的数值分析[J].岩石力学与工程学报,2005,24(11): 3978-3982.
[12] 徐前卫,尤春安,朱合华.预应力锚索的三维数值模拟及其应用研究[J].岩石力学与工程学报,2004,23(2): 4941-4945.
[13] 王敏强,刘晓刚 .某厂房边坡施工过程仿真及稳定分析[J].岩石力学与工程学报,2002,21(增2):2506-2510.
[14] 丁秀丽,盛 谦,韩 军,等.预应力锚索锚固机理的数值模拟试验研究[J].岩石力学与工程学报,2002,21 (7):980-988.
[15] 郑筱彦.预应力锚索对岩质边坡加固效应的数值模拟[J].华中科技大学学报:自然科学版,2011,39(7):118-122.
[16] 郑明新.预应力锚索抗滑桩中预拉力合理值的探讨[J].力学与实践,2011,33(5):16-20.
[17] 王忠昶,栾茂田,杨 庆,等.裂隙岩体锚固止裂的数值模拟研究[J].岩石力学与工程学报,2007,26(增1):3446-3451.
[18] 李 宁,张 鹏 ,于 冲.边坡预应力锚索加固的数值模拟方法研究[J].岩石力学与工程学报 ,2007,26(2): 254-261.
中图分类号:TU476
文献标识码:A
文章编号:1672—1144(2015)01—0020—06
DOI:10.3969/j.issn.1672-1144.2015.01.005
收稿日期 :2014-09-06修稿日期:2014-10-17
基金项目 :福建省自然科学基金资助项目(2011J01308)
作者简介 :徐 祥(1985—),男,河南尉氏人,博士研究生,研究方向为岩土体稳定性分析及岩土工程有限元子程序开发及应用。E-mail:xuxiang20040071@126.com
通信作者 :戴自航(1966—),男,湖南长沙人,博士 ,教授 ,博士生导师,主要从事边坡稳定分析、滑坡治理、建筑基础、深基坑支护等方面的教学与研究工作。E-mail:Mr.dai@163.com
Equivalent Force Method of 3D Numerical Simulation on Prestressed Anchorage Effect of Rock and Soil
XU Xiang1,DAI Zi-hang1,2
(1.Institute of Geotechnical engineering,Fuzhou University,Fuzhou,Fujian 350108,China;2.School of Civil,Mining and Environmental Engineering,University of Wollongong,NSW 2522,Australia)
Abstract:The issue of rock and soil reinforced with prestressed anchor cables(rods)is a typical spatial interaction issue between structure and rock-soil.In order to reliably simulate this kind of interaction,an equivalent force method which agreed with the working conditions of prestress loading and locking was presented in 3D numerical analysis.On the platform of the finite element software ABAQUS,firstly,the numerical modeling test of a single prestressed anchor cable was conducted.It demonstrates the superiority of the equivalent force method compared with the existing equivalent lowering temperature method and equivalent strain method.Meanwhile,the analysis shows that the declining rates of the axial forces of the anchor cables are related with the stiffness of anchorage body and the outcomes are consistent with the theoretical ones.Then based on a practical slope reinforcement engineering,the application of the equivalent force method was introduced in the 3D numerical modeling of a slope reinforced with prestressed anchors.It indicates that this method can be reliably applied to analyze the reinforcement effect of rock and soil with prestressed anchors and the internal forces of anchors’themselves.
Keywords:prestressed anchor cable;interaction;equivalent force method;axial force of anchor cable;slope reinforcement;stability factor

