基于无失效变形监测数据的大坝整体安全度评价

方卫华，吴健琨

（1.水利部南京水利水文自动化研究所，江苏南京210012；2.水利部水文水资源工程监控研究中心，江苏南京210012）

基于无失效变形监测数据的大坝整体安全度评价

方卫华1，2，吴健琨1

（1.水利部南京水利水文自动化研究所，江苏南京210012；2.水利部水文水资源工程监控研究中心，江苏南京210012）

摘要:针对所有测点测值都属于正常的大坝整体安全度评价问题 ，充分利用多测点信息，在假设大坝各个测点为总体的一个抽样的条件下，应用水工结构知识和Vanmarcke相关距离方法确定独立的测点群，通过各批次独立测点群及其正常工作时间获取无失效数据，在此基础上应用变形监测数据对某重力拱坝的整体安全度进行评价，工程实例证明了本方法的可行性和有效性。

关键词:E-Bayes理论；无失效数据；整体安全度；多尺度评价；重力拱坝

1　概 述

由于大坝等水工建筑物安全的重要性和复杂性，应用原型实测数据进行工程安全评价一直是学术界研究的重点和难点。经过广大学者的努力，应用实测资料对工程安全度进行评价的方法有很多，如时空分析法、监控指标法、突变论法、工程类比法以及不确定综合评价法等［1-2］，尽管上述方法都具有各自优势，但上述方法对各个测点测值都很“正常”的工程安全整体评价问题针对性不强。实际上，即使大坝安全监测系统中全部测点测值都很正常，大坝整体安全度也不可能是100%。有许多工程，特别是大型工程基于实测资料的大坝安全评价中碰到了上述问题。经过相关文献检索，尚未见到有效解决上述问题的方法。为解决上述问题，考虑到正常设计、施工和管理的大坝是一个高可靠性系统，当将大坝各个测点作为代表大坝安全状态的总体一个抽样时，各个测点分别为来自总体的一个截尾可靠性实验，选择其中全部独立多测点（认为其信息对评估大坝安全而言是完备的），当全部独立测点测值都在“正常”范围内时候，应用无失效数据理论（Zerofailure data theory）综合实测信息从整体上定量评估大坝安全度。

2　相关理论

无失效数据可表示为（ni，ti），其中 ni（i=1，2，…k）为第i批次建成投运的独立测点数量（单位为个），k为截止目前为止总共建成投运的测点批次数量（单位为批），各批次测点到目前为止所对应的截尾时间为为在ti时刻不能肯定是否会失效的测点（样本）数。针对小样本、高可靠、长寿命系统的可靠度评估，无失效数据分析理论是有效方法。Bartholomew D.J、茆诗松、Berger J.O、韩明、Shao J以及王玲玲等对无失效数据理论进行了大量的研究 ，并将其用于火箭（发动机）等高可靠性系统的可靠性评估［3-10］。

2.1应用前提分析

无失效数据理论应用前提:（1）要求所有测点测值正常，为此首先必须对所有测点测值进行分析以判定大坝状态是否正常。测点测值分析方法很多，具体分析方法和步骤可参见文献［1-2］。（2）选择相对独立测点并假设大坝整体寿命分布，对于前者将在2.2小节进行说明。针对大坝这一类高可靠性系统寿命分布可选用形状参数和特征寿命分别为m、η的Weibull分布:

2.2独立测点选择

设 i批次建成投运并稳定运行至今的有ni个测点，如在运行过程中有测点损坏则不计入 ni。ni个两个测值正常测点分别称为j和k，概率独立性条件要求该两个测点测值序列 Xj、Xk必须满足

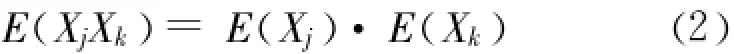
在实际工程中，由于监测仪器测值误差客观存在以及样本容量有限等原因 ，即使两个测点独立，其对应的两个测值序列也很难满足式（2），即使在不同大坝上的两个测点，按式（2）判断也很难判别其独立性。在水位、温度和蠕变等因素作用下，每个测点测值序列严格意义上讲都是一个非平稳过程，应用式（2）进行独立性判断难以准确刻画两测值序列之间的相关关系，为此依据以下原则判别测点是否独立:

（1）分别位于坝体和坝基上的测点之间是独立的，在坝体上被纵、横缝分开的测点是独立的，在坝基上被大坝分开或被断层分开的测点是独立的。

（2）相隔1年以上不同时间建成投运的测点是独立的。

（3）安装在相同的横、纵缝之间或同一个完整基础上的两个测点，其独立性由Vanmarcke相关距离确定［11-12］。对于安装在相同的横、纵缝之间或同一个完整基础上的多个测点 ，其独立测点选择的过程是先选取测值平均年变幅最大的测点 ，再以该测点为基准选择其Vanmarcke相关距离外的测点，再在此测点相关距离外选择测值平均年变幅的测点。依此类推，直到相同的横、纵缝之间或同一个完整基础上的全部测点分划完为止。

2.3pi的E-Bayes估计

π（b）表示 b的先验概率密度函数 （Prior probability density function，PPDF），其中 b∈（1，c）为超参数，一般情况可令 c＞1为 b∈（1，c）的上界，理由将在下文分析。根据2.1小节的假设，pi的概率密度函数表示为:

（0，1），a∈（0，+∞），b∈（0，+∞）。在坝体和基础未加固条件下，由于坝体、坝基材料力学性质的降低和结构的老化，大坝整体安全度是逐年降低的，为此选择参数 a、b应使得先验分布π（pi|a，b）为pi的非增函数，为此必须要求参数 a、b满足:0＜a≤1 且b＞1。在此基础上将pi的Bayes估计写成＾pi（b），则称pi的E-Bayes估计为＾piEB=∫Ω＾pi（b）π（b）db。

由Beta概率分布的特征可知，b宜选取比较小的值，其理由是（1）当 a=1，随着b的增大，密度函数的尾部就越拖。（2）随着 b的增大，先验分布的Bayes估计就越不稳定。为此，在应用E-Bayes估计时应根据研究对象的概率特征对参数进行优化。当a=1，pi的PPDF为:

根据式（4）可由Bayes定理获得 pi的Bayes估计。若 pi的PPDF由式（1）给出，则在平方损失下 pi 的Bayes估计为［4-10］:

在式（5）条件下若b的PPDF为:

则可以得到 pi相应的E-Bayes估计＾pi为:

2.4可靠性的点估计

2.4.1 等权估计

根据2.1和文献［8］，参数η、m等权条件下的最小二乘估计分别为:

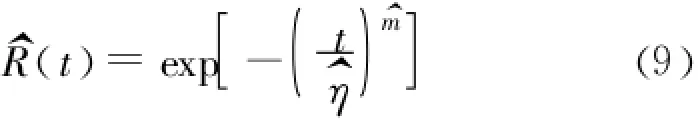
2.4.2 不等权估计

根据2.1和文献［7］，对于不等权情况，参数 η、m各自的加权最小二乘估计分别为

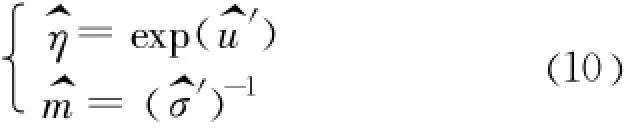
对应大坝t时刻整体安全度为

2.5安全度的区间估计

设置信度为α，则Weibull分布参数η的双侧置信上、下限分别为［3-9］:

置信度为（1-α）的大坝整体安全度R（t）的双侧置信上、下限分别为:

根据式（14）可以得到置信度为（1-α）条件下大坝整体安全度的区间估计为

3　工程实例

大唐国际某水电站枢纽主要建筑物混凝土重力拱坝由28个坝块组成，整个坝顶弧长共419 m，坝顶宽8 m，最大坝高为76.3 m，对应最大坝底宽53.2 m。

为监测大坝安全 ，在大坝不同坝段和坝基（肩）不同高程共布置正倒垂线19个测点进行变形监测，整个测点遍布大坝安全关键部位 ，各批次建成投运的变形测点数量及其时间如表1所示。其中IP表示倒垂线，LP表示正垂线，U表示一根垂线的上部测点，B表示一根垂线的下部测点。由于该坝布置的变形测点较多，监测范围涉及整个大坝的各个关键部位，因此认为全部变形测点已经包含大坝整体安全信息。采用文献［1-2］的方法分析各个变形测点测值情况，发现各个测点测值都在正常范围内且无趋势性变化，与数值模拟和类似工程比较各测点测值规律正常。采用上文2.1节方法，表1中全部19个测点测值满足独立性要求 ，由此构造的无失效数据如表2所示。

根据式（9）试算，发现当 c分别取3、4或5时，计算结果相差很小。为此，c=4的计算结果见表3。

通过表3中大坝整体失效概率的点估计不难发现，随着时间的发展，大坝整体失效概率逐年增大。根据式（11）和式（14）可得到大坝整体安全度的点/区间估计，结果见表4～表6。由表可知，大坝如按照当前的发展趋势，该坝到50 a后整体失效概率为20%，到100 a后，大坝失效概率大于50%，通俗地讲该坝在50 a内可以基本保持稳定，但到100 a后如不采取有效措施大坝失事概率很大。

表1　全部各批次建成投运变形测点统计表

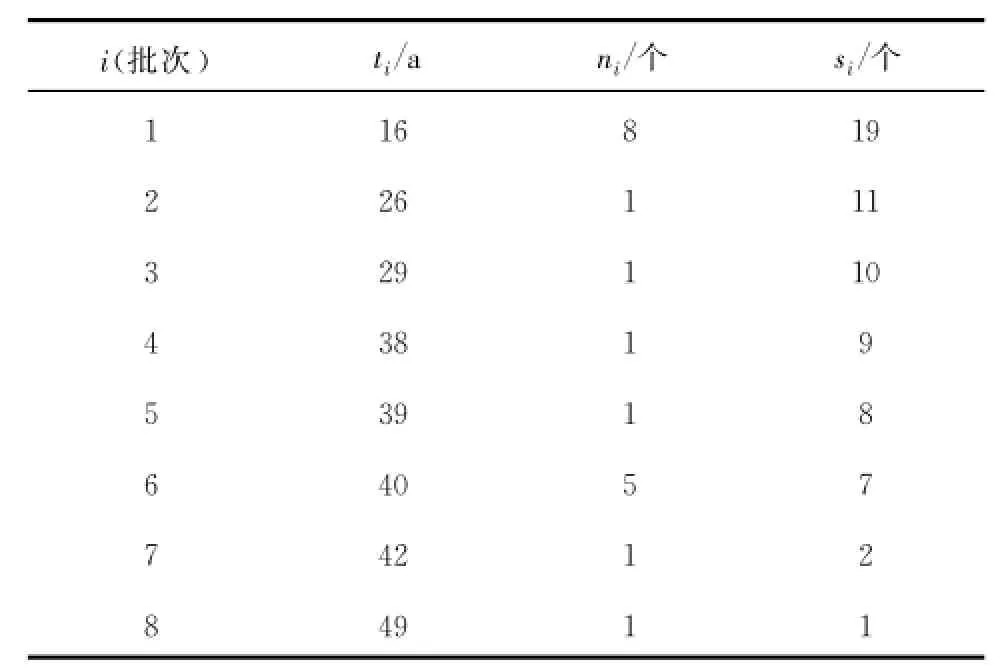
表2　无失效变形监测数据汇总表

表3　大坝整体失效概率＾pi的估计

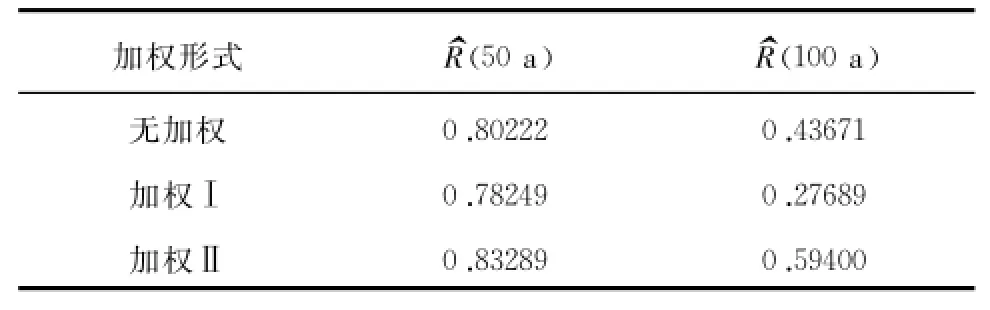
表4　50 a/100 a后大坝整体可靠度＾R的点估计

表5　50 a 后大坝整体可靠度信限区间估计

表6　100 a后大坝整体可靠度区间估计

4　结 语

（1）将多个多批次测点看成大坝整体的不同抽样，采用多测点进行大坝整体安全度估计充分利用了各批次测点信息。

（2）应用无失效数据分析理论有效解决了大坝所有测点实测数据都属于“正常”范围条件下的大坝安全评价问题，通过构造无失效数据获得了大坝整体安全度的点（区间）估计。

（3）应用不同时间和空间的无失效数据，利用本文的方法可以实现工程安全的时间/空间多尺度评价。

（4）大坝安全度满足Weibull的假设等假设条件是否对各类工程都适用，还需在理论和实践上进行更多的证明和检验。

参考文献:

［1］ 吴中如.水工建筑物安全监控理论及应用［M］.北京:高等教育出版社，2003.

［2］ 方卫华.大坝安全监控:问题、观点与方法［M］.南京:河海大学出版社，2013.

［3］ Chow S C，Shao J.Estimation drug shelf-life with random batches［J］.Biometrics，1991，47（9）:1071-1079.

［4］ 茆诗松，王玲玲，濮晓龙.威布尔分布场合无失效数据的可靠性分析［J］.应用概率统计，1996，12（1）:94-107.

［5］ 韩 明.基于无失效数据的可靠性参数估计［M］.北京:中国统计出版社，2005.

［6］ 韩 明.某型发动机无失效数据的Bayes可靠性分析［J］.航空学报，1999，20（3）:216-219.

［7］ 宁江凡，鄢小清，张士峰.液体火箭发动机无失效条件下的可靠性分析方法［J］.国防科技大学学报 ，2006，28 （5）:22-25.

［8］ 韩 明.无失效数据下液体火箭发动机的E-Bayes可靠性分析［J］.航空学报，2011，32（12）:2213-2219.

［9］ 韩 明.Weibull分布可靠性参数的置信限［J］.机械强度，2009，31（1）:59-62.

［10］ 韩 明.失效概率的E-Bayes估计及其性质［J］.数学物理学报:A辑，2007，27（3）:488-495.

［11］ Vanmarcke Erik H.Probabilistic modeling of soil profiles ［J］.Journal of the Geotechnical Engineering Division.ASCE，1977，103（11）:1227-1246.

［12］ 徐 斌，王大通 ，高大钊.用相关函数法求静探曲线相关距离的讨论［J］.岩土力学，1998，19（1）:55-58.

中图分类号:TV642.4

文献标识码:A

文章编号:1672—1144（2015）01—0011—05

DOI:10.3969/j.issn.1672-1144.2015.01.003

收稿日期 :2014-10-07修稿日期:2014-11-04

基金项目 :中央级公益性科研院所基本科研业务经费资助青年项目（Y914010）

作者简介 :方卫华（1972—），男，安徽安庆人，博士 ，教授级高级工程师，主要从事大坝安全监控和工程力学方面的研究工作。E-mail:13813843565@139.com

Dam Safety Evaluation Based on Zero-Failure Data of Deformation Monitoring

FANG Wei-hua，WU Jian-kun
（1.Nanjing Automation Institute of Water Conservancy and Hydrology，Nanjing，Jiangsu 210012，China；2.Engineering Research and Monitoring Center of Water Resources and Hydrology，Nanjing，Jiangsu 210012，China）

Abstract:Here，the information of multiple monitoring points in the dam safety monitoring system was fully used to determine the independent monitoring point groups on the assumption that the values of monitoring points are set under the same sampling regarding to the integral safety evaluation of the dams with all regular monitoring data.In order to select the independent monitoring point groups，Vanmarcke correlation distance method combined with hydro-structure knowledge were used to obtain the zero-failure data based on the independent monitoring point groups in every batch and their normal operating hours.The case study of a gravity-arch dam proves that this method is effective and practicable.

Keywords:E-Bayes theory；zero-failure data；integral safety degree；multi-scale evaluation；gravity-arch dam