Robust Tracking Control of Uncertain MIMO Nonlinear Systems with Application to UAVs

Yanlong Zhou,Mou Chen,and Changsheng Jiang

Robust Tracking Control of Uncertain MIMO Nonlinear Systems with Application to UAVs

Yanlong Zhou,Mou Chen,and Changsheng Jiang

—In this paper,we consider the robust adaptive tracking control of uncertain multi-input and multi-output (MIMO)nonlinear systems with input saturation and unknown externaldisturbance.The nonlinear disturbance observer(NDO) is employed to tackle the system uncertainty as well as the externaldisturbance.To handle the input saturation,an auxiliary system is constructed as a saturation compensator.By using the backstepping technique and the dynamic surface method, a robust adaptive tracking control scheme is developed.The closed-loop system is proved to be uniformly ultimately bounded thorough Lyapunov stability analysis.Simulation results with application to an unmanned aerial vehicle(UAV)demonstrate the effectiveness of the proposed robust control scheme.

Index Terms—Nonlinear system,unmanned aerial vehicle(UAV),input saturation,disturbance observer,backstepping control,dynamic surface control(DSC).

I.INTRODUCTION

N OWADAYS,unmanned aerialvehicles(UAVs)have been widely used in both military and civilian areas due to their low cost,high maneuverability,no casualty,etc[1−4].In a sense,UAVs show a valuable prospect for some applications where human interventions are restricted.To achieve a successfulmission,the robustadaptive tracking controldesign for UAVs needs to be excellent because of the absence of a human pilot.Thus,it has attracted an increasing interest around the world in recentyears.In[5],a high-levelcontroller for a fixed-wing UAV was developed based on the nonlinear model predictive control method through an error dynamics. In[6],the output-feedback control scheme was proposed for an underactuated quadrotor UAV using neural networks.In [7],an optimal controller was designed for helicopter UAVs, and the optimal trajectory tracking was accomplished by a single neural network.To increase the robustness,a sliding mode controller and an adaptive controller were presented in [8]and[9],respectively.However,as a kind of multi-input and multi-output(MIMO)nonlinear systems,the design of robust flight control is complex for UAVs with parameter uncertainty,strong nonlinearity,high coupling and unknown external disturbance.Fortunately,the nonlinear disturbance observer(NDO)is proven to be an effective method to handlesystem uncertainty and unknown external disturbance[10−14]. The robustcontroldesign based on the NDO has been successfully applied to air vehicles.In[10−13],under the condition thatthe derivative of the compounded disturbance was closely equal to zero,a disturbance observer technique was proposed. Actually,the compounded disturbance is changeable with time for UAVs.To relax this assumption of the above mentioned NDO,we need to further develop and apply it to the robust control design of UAVs.

For some specialclasses of nonlinear systems,backstepping is an important control approach[15−19],which is a Lyapunovbased recursive design procedure.In[16−18],an adaptive tracking control framework for a class of uncertain nonlinear systems was studied based on radial basis function neural networks.The adaptive control scheme was developed for MIMO nonlinear systems considering time-varying delays and unknown backlash-like hysteresis in[19].However,there exists the problem of calculation explosion in the conventional backstepping technique.The dynamic surface control (DSC)[20−24]was proposed to solve this problem by introducing a first-order filter at each step.As a result,the derivative of the virtual control law was avoided to be calculated,which simplified the design process.In[20],the dynamic surface technique was described in detail by Swaroop et al.,and furtherdeveloped in[21−24].In this paper,the robustadaptive tracking control for UAVs is designed based on the DSC.

On the other hand,the rudder deflections of UAVs are limited.If we ignore inputsaturation in the controldesign,the system control performance can be degraded and the system instability can be caused,even a serious accidentwillhappen. During the past decades,various schemes for the control design of nonlinear systems with input saturation have been studied extensively.In[25−27],a robustadaptive controlwas proposed based on the backstepping technique,using the specialproperty of a hyperbolic tangentfunction and a Nussbaum function to handle the input saturation.In[28−30],an auxiliary system was constructed as a compensator to eliminate the effect of the input saturation,which was successfully applied to the controldesign ofocean surface vessels.By regarding the input saturation as a kind of constraints for the optimization function,the predictive controlwas studied[31−32].In[33−34], an adaptive dynamic programming approach was proposed by employing a generalized non-quadratic function to deal with control constraints.However,there are few existing works about tracking control for UAVs with input saturation and unknown external disturbance.

Motivated by the above discussion and analysis,a robust adaptive tracking control scheme is proposed for a class of uncertain MIMO nonlinear systems in the presence of system uncertainty,unknown external disturbance,and input saturation.To efficiently handle the compounded disturbance,the NDO is employed.The auxiliary system is designed to eliminate the effect of input saturation.The advantage of the dynamic surface technique is taken to deal with the explosion of complexity in backstepping control.The stability of the closed-loop system based on the developed robust adaptive tracking control scheme is rigorously analyzed through Lyapunov method.Finally,the developed robust adaptive tracking control scheme is used for the flight control design of UAVs. The organization of the paper is as follows.In Section II,the problem is described.Section III presents the design of the NDO.The robust adaptive tracking controlis investigated for uncertain MIMO nonlinearsystems by considering system uncertainty,unknown external disturbance,and input saturation in Section IV.In Section V,simulation results of a UAV are given to illustrate its effectiveness,followed by concluding remarks in Section VI.

II.PROBLEM STATEMENT

Consider a class of uncertain MIMO nonlinear systems in the presence of input saturation,given as follows:

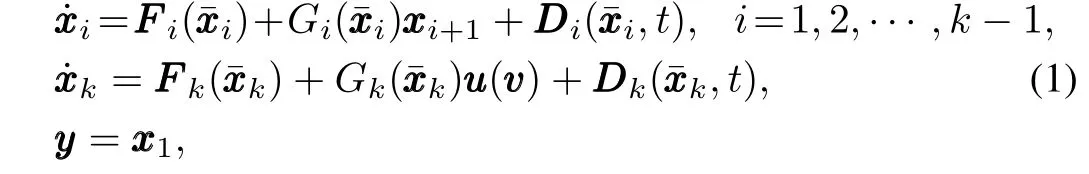
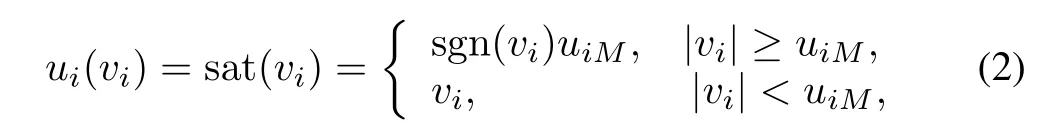
where uiMis the bound of ui(vi),i=1,2,···,m,sgn(·) stands for the sign function.

In this paper,the controlobjective is designing the adaptive control law vvv to make the closed-loop system stable and to rend yyy following the given desired trajectory yyyrin the presence of system uncertainty,unknown externaldisturbanceof the disturbance observer,ˆςjis the estimated value of¯ςj, γj＞0 and pi＞0 are designed parameters,i=1,2,···,k. To develop the robust adaptive tracking control scheme for the uncertain MIMO nonlinear system(1),the following assumptions and lemmas are required.

Assumption 1.For the uncertain MIMO nonlinear system (1),all states of the system are measurable.

Assumption 2[23].For the uncertain MIMO nonlinear system(1),the desired trajectory yyyrand ˙yyyr(t),¨yyyr(t)are bounded,that is,there exists a constant B0＞ 0,such that Π0:={(yyyr,˙yyyr,¨yyyr):||yyyr||2+||˙yyyr||2+||¨yyyr||2≤ B0},‖·‖ represents the Frobenius norm for a matrix or the Euclidean norm for a vector.

Assumption 3[14].For the uncertain MIMO nonlinear system(1),the derivative of the compounded disturbance is bounded,that is,‖˙DDDi‖≤ βdi,whereβdi＞ 0 is unknown, i=1,2,···,k.

Assumption 4[35].For the uncertain MIMO nonlinear system(1),the inverse matrix of Gi∈ Rn×nexists,i= 1,2,···,k−1,and the generalized inverse matrix of Gk∈Rn×mexists.On the otherhand,there exists positive constant

Lemma 1[36].For anyρ＞0 and¯zzz=[¯z1,¯z2,···,¯zn]T∈Rn,the following inequality always holds:

where tanh(¯zzz/ρ)=[tanh(¯z1/ρ),tanh(¯z2/ρ),···,tanh(¯zn/ ρ)]T,¯κ=nζ0,n is the dimension of vector¯z,ζ0is a constant satisfyingζ0=e−(ζ0+1),that is,ζ0=0.2785.

Lemma 2[37].For bounded initial conditions,if there exists a C1continuous and positive-definite Lyapunov function V(xxx)satisfyingπ1(‖xxx‖)≤ V(xxx)≤ π2(‖xxx‖),such that ˙V(xxx)≤ −κV(xxx)+c,whereπ1,π2:Rn→ R are class K functions andκ,c are positive constants,then the solution xxx(t)is uniformly bounded.

Remark 1.Fora practicalsystem,the derivative ofthe compounded disturbance should be bounded.Otherwise,the compounded disturbance willbe infinite and is quickly changeable with time.This compounded disturbance does not exist in UAV.Thus,Assumption 3 is reasonable.

III.DESIGN OF NDO

Since the compounded disturbance of the uncertain MIMO nonlinear system(1)is unknown,it cannot be directly used to design the robust adaptive tracking controller.To efficiently deal with this,the NDO is employed.For the convenience of robust adaptive tracking control development,the NDO is described as follows[14].

In a general way,each subsystem of(1)can be written as the following uncertain MIMO nonlinear system given by

where xxx∈Rnis the state vector,uuu∈Rmis the control input vector,FFF(xxx)∈Rnand G(xxx)∈Rn×mare known smooth functions of xxx,DDD(xxx,t)=ΔFFF(xxx)+ddde(t)is the unknown compounded disturbance,ΔFFF(xxx)stands for the system uncertainty,and ddde(t)represents the external disturbance.DDD(xxx,t) satisfies the assumption of the compounded disturbance,that is,‖˙DDD‖≤βd,whereβd＞0 is unknown.

To approximate the compounded disturbance of system(4), we design the following NDO:

whereη∈Rnis the internalstate of the disturbance observer, PPP(xxx)=[P1(xxx),P2(xxx),···,Pn(xxx)]T∈Rnis the designed function vector which should make the constant matrix L=

The error of the disturbance observer is defined as

The following lemma aboutthe disturbance observer design is given,which includes the convergence of the disturbance approximation error.

Lemma 3.Consider the uncertain MIMO nonlinear system (4)satisfying the assumption of the compounded disturbance. If the NDO is designed as(5)and(6),then the disturbance approximation error˜DDD is bounded.

Proof.Choose the Lyapunov function as

Differentiating(7)and considering(4)～(6),we have

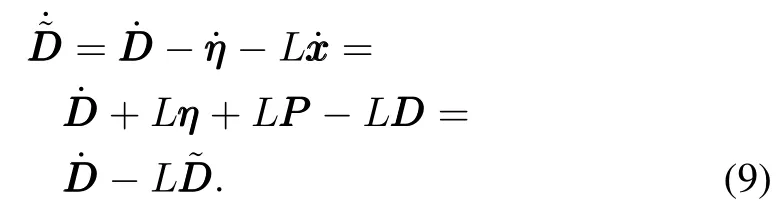
Considering(9),the time derivative of V0is given by

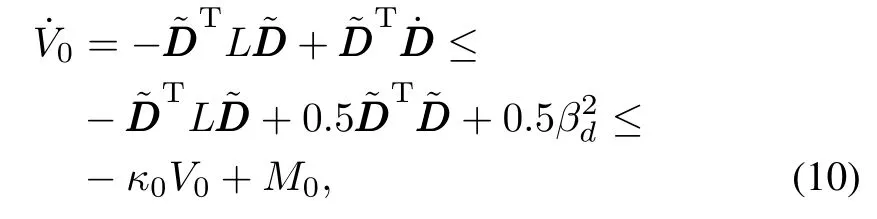
whereκ0=2λmin(L)−1＞0,and M0=0.5β2d＞0. Integration of(10)yields

According to(11)and Lemma 2,we can obtain that the disturbance approximation error is bounded and satisfies the following inequality:

This concludes the proof.

IV.ROBUST ADAPTIVE TRACKING CONTROL DESIGN BASED ON NDO

In this section,the robustadaptive tracking scheme will be proposed for the uncertain MIMO nonlinear system(1)by combining the dynamic surface approach with backstepping technique based on the NDO,and an auxiliary system is constructed to solve the problem of input saturation.The detailed design procedure is described as follows.

Step 1.Employ the NDO to approximate the compounded disturbance DDD1which can be described as

whereη1∈ Rnis the internal state of the disturbance observer,PPP1∈ Rnis the designed function vector,and L1=The approximation error of the first disturbance observer is defined as

We know that˜DDD1is bounded according to Lemma 3,and assume that‖˜DDD1‖≤¯ς1.

Define

The virtual control law is designed as

where C1= CT1＞ 0 andρ1＞ 0 are designed parameters,ˆς1is the estimated value of¯ς1,tanh(zzz1/ρ1)= [tanh(z1,1/ρ1),tanh(z1,2/ρ1),···,tanh(z1,n/ρ1)]T, and zzz1=[z1,1,z1,2,···,z1,n]T.

To solve the explosion ofcomplexity in the traditionalbackstepping control,the dynamic surface method is employed. Namely,we make the virtual control law¯α1pass through a first-order filter,i.e.,

whereΓ1=diag{τ1,1,τ1,2,···,τ1,n},τ1,j＞0 is the time constant of the first-order filter,j=1,2,···,n.

Define

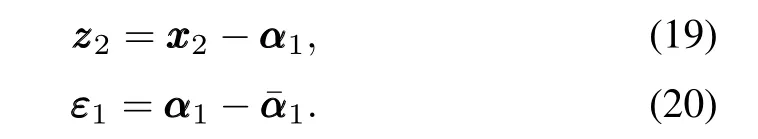
Considering(1),(15),(17),(19)and(20),the time derivative of zzz1can be expressed as

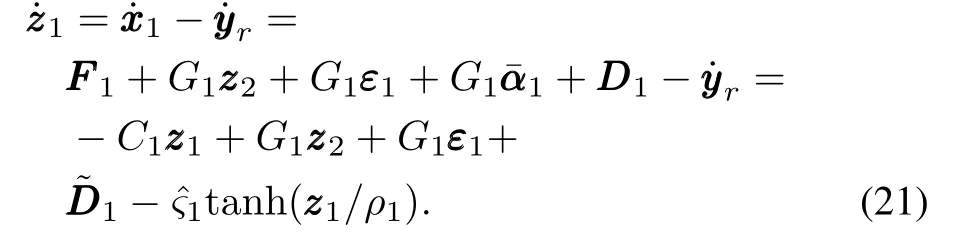
Differentiating(20),we have

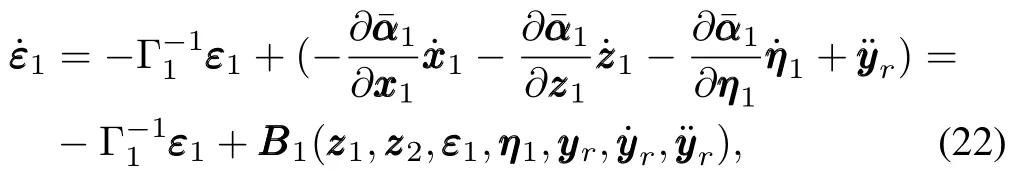
where BBB1(·)is a continuous function with respectto variables (zzz1,zzz2,ε1,η1,yyyr,˙yyyr,¨yyyr).Since setsΠ0∈ R3mandΠ1∈R2n+1are compact,Π0×Π1is also compact.The maximum value¯BBB1of function BBB1(·)exists onΠ0×Π1because of the continuous function property[23].Therefore,we have

whereγ1＞ 0 is a designed parameter,˜ς1= ¯ς1−ˆς1,and ˙˜ς1= −˙ˆς1.

Differentiating(24)and considering(21)and(23),we obtain

The parameter adaptive law is chosen as

where k1＞0 is a designed parameter.

Substituting(26)into(25)yields

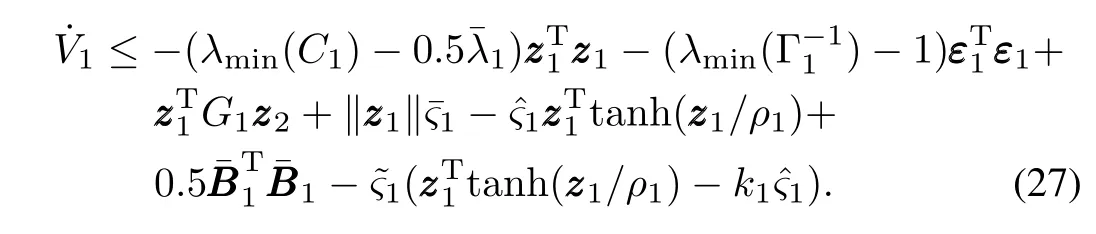
By Lemma 1,the following inequality holds:

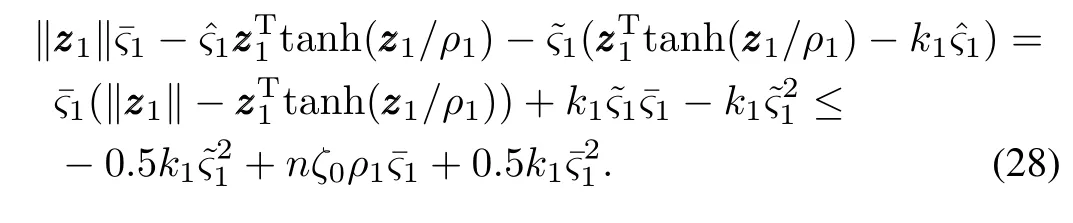
Substituting(28)into(27),we have

S tep iii(222≤iii≤kkk −111).Employ the NDO to approximate the compounded disturbance DDDiwhich can be described as

whereηi∈ Rnis the internal state of the disturbance observer,PPPi∈ Rnis the designed function vector,andThe approximation error of the i-th disturbance observer is defined as

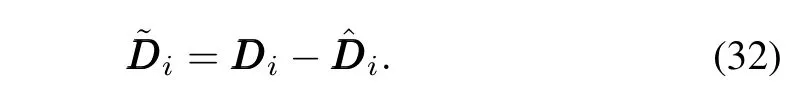
We know that˜DDDiis bounded according to Lemma 3,and assume that‖˜DDDi‖≤¯ςi.

Define

The virtual control law is designed as

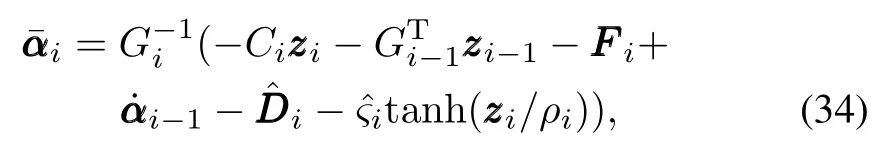
where Ci= CTi＞ 0 andρi＞ 0 are designed parameters,ˆςiis the estimated value of¯ςi,tanh(zzzi/ρi)= [tanh(zi,1/ρi),tanh(zi,2/ρi),···,tanh(zi,n/ρi)]T,and zzzi= [zi,1,zi,2,···,zi,n]T.

We make the virtualcontrollaw¯αipass through a first-order filter,i.e.,

whereΓi=diag{τi,1,τi,2,···,τi,n},τi,j＞ 0 is the time constant of the first-order filter,j=1,2,···,n.

Define

Considering(1),(32),(34),(36)and(37),the time derivative of zzzican be expressed as

Differentiating(37),we have

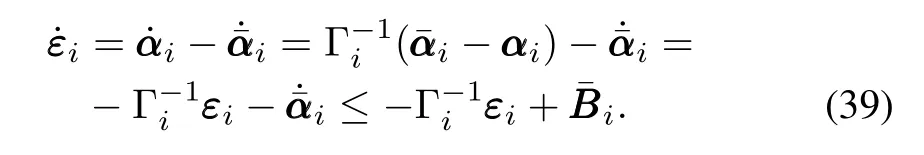
Consider the Lyapunov function as

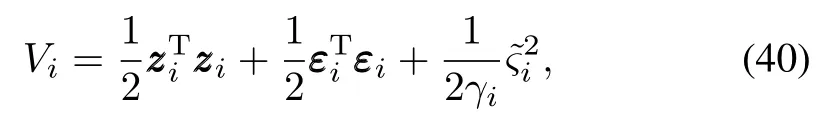
whereγi＞0 is a designed parameter,=

Differentiating(40)and considering(38)and(39),we obtain

The parameter adaptive law is chosen as

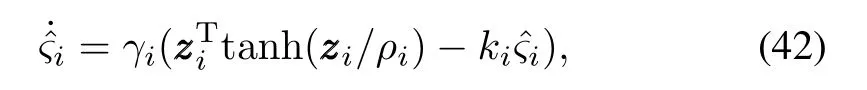
where ki＞0 is a designed parameter.

Substituting(42)into(41)and invoking Lemma 1,we obtain

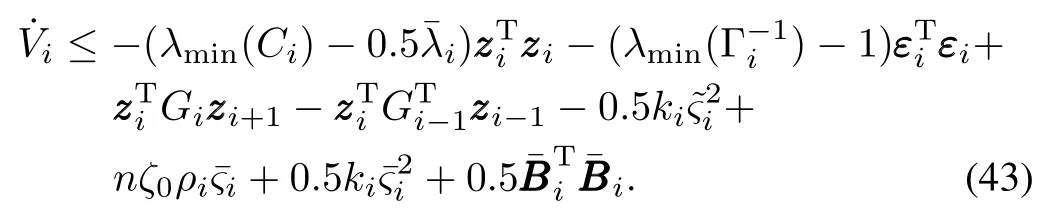
Step kkk.Employ the NDO to approximate the compounded disturbance DDDkwhich can be described as

whereηk∈ Rnis the internal state of the disturbance observer,PPPk∈ Rnis the designed function vector,and.The approximation error of the k-th disturbance observer is defined as

We know that˜DDDkis bounded according to Lemma 3,and assume that‖˜DDDk‖≤¯ςk.

Define

Considering(1),the time derivative of zzzkcan be expressed as

Consider the Lyapunov function as

whereγk＞0 is a designed parameter,˜ςk=ςk−ˆςk,ˆςkis the estimated value of¯ςk,and˙˜ςk=−˙ˆςk.

Differentiating(49)and considering(48),we obtain

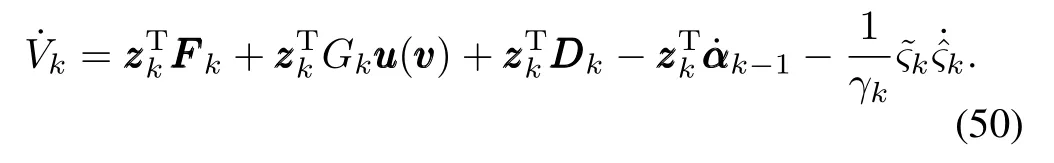
The parameter adaptive law is chosen as

whereρk＞0 and kk＞0 are the designed parameters,tanh (zzzk/ρk) = [tanh(zk,1/ρk),tanh(zk,2/ρk),···,tanh(zk,n/ ρk)]T,and zzzk=[zk,1,zk,2,···,zk,n]T.

Substituting(51)into(50),we obtain

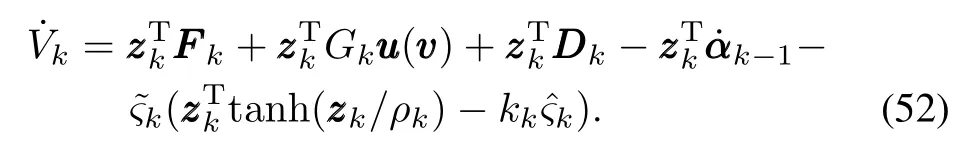
To eliminate the effect of the input saturation,we have the following auxiliary design system[28−30]:

where C0=CT0＞0 andε0＞0 are designed parameters,and ξ=uuu(vvv)−vvv is the input-output difference of the actuator.

Considering the input saturation,we design the following control law:

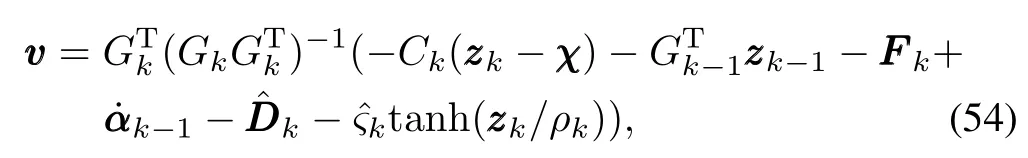
where Ck=CTk＞0 is a designed matrix.

According to above analysis,the following theorem is proposed.

Theorem 1.Considerthe uncertain MIMO nonlinear system (1)satisfying Assumptions 1～4.The nonlineardisturbance is given as(13),(14),(30),(31),(44)and(45),and parameter adaptive laws are chosen as(26),(42)and(51),and the auxiliary system is designed as(53).Under the control laws (17),(34)and(54),all signals of the closed-loop system are uniformly ultimately bounded.

Proof.If‖χ‖≥ε0,choose the Lyapunov function as

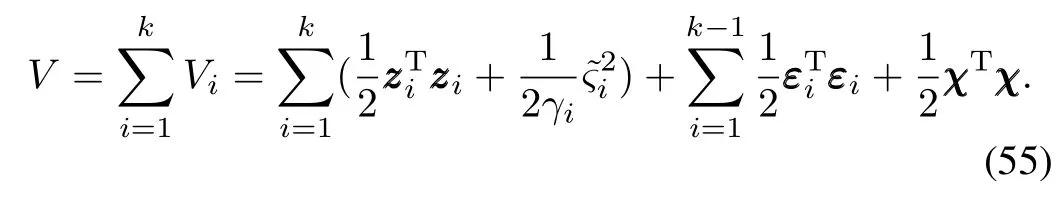
Considering(29),(43),(52),(53)and invoking Lemma 1, we obtain the time derivative of V as follows:

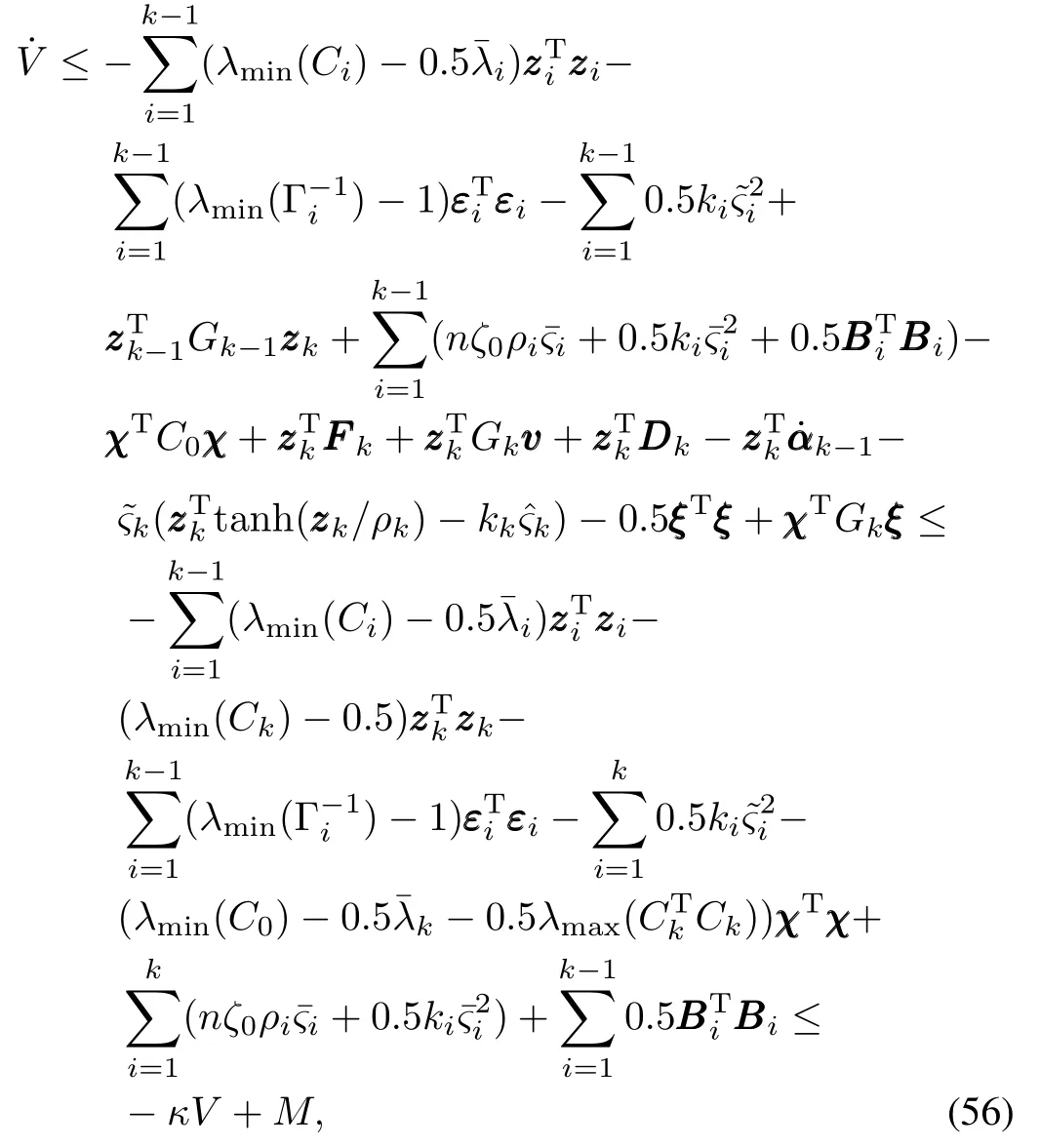
According to(57)and Lemma 2,we can obtain that all signals of the closed-loop system are uniformly ultimately bounded.

On the other hand,there does not exist input saturation in the control system if‖χ‖＜ε0,that is,uuu(vvv)=vvv.Under this circumstance,Theorem 1 can be easily proved with similar processes.

This concludes the proof. □

Remark 2.For the auxiliary system(53),we calculate the firstequation when the saturation phenomenon appears in the simulation.If‖χ‖＜ ε0andξ/=0,the initial value ofχis reset to eliminate the effect of input saturation.

V.SIMULATION STUDY FOR UAV

In this section,we apply the proposed robustcontrolscheme to the attitude tracking control of a UAV to illustrate the effectiveness.The considered attitude dynamic model of the UAV can be written as the following two MIMO nonlinear systems in accordance with singularly perturbed theory and time-scale separation principle[38]:

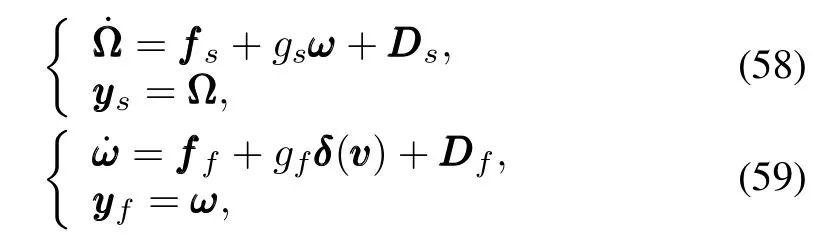
whereΩ=[α,β,µ]Tis the vector of attitude angles,including angle of attack,sideslip angle and roll angle,ω=[p,q,r]Tis the vector of attitude angular rates,including angular rate,pitch angular rate and yaw angular rate.In the slowloop equation,fffsis the state functional vector,gsis the system matrix,DDDs=Δfffs+dddsis the unknown compounded disturbance,Δfffsrepresents the system uncertainty,dddsstands for the external disturbance.In the fast-loop equation,ffffis the state functional vector,gf=gf1gfδ,where gf1is the system matrix,gfδis the allocation matrix of rudders, DDDf=Δffff+dddfis the unknown compounded disturbance, Δffffrepresents the system uncertainty,dddfstands for the external disturbance,vvv=[v1,v2,v3,v4,v5]Tis the control inputvector,δ(vvv)=[δa,δe,δr,δy,δz]Tdenotes the plantinput vectorsubjectto saturation nonlinearity,involving ailerons,elevator,rudder,lateral deflection and longitudinal deflection of the thrust vectoring control surface.The detailed expressions of corresponding terms in(58)and(59)can be found in[38].

The initial conditions for the UAV are chosen asα0=2°, β0=1°,µ0=0°,p0=q0=r0=0 rad/s,δaM=δeM= δrM=30°,andδyM=δzM=15°.The desired attitudes are chosen as

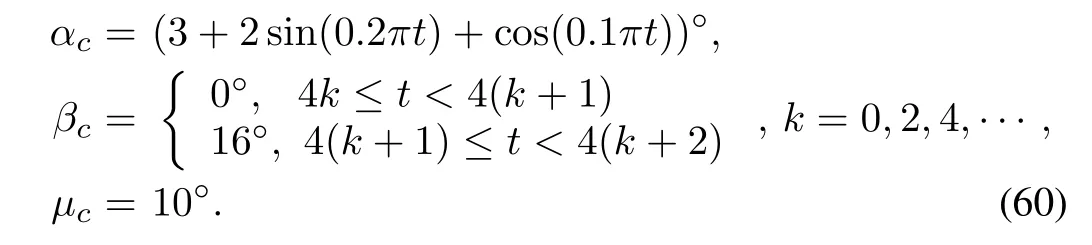
Suppose that there are+30%and−30%uncertainties on aerodynamic coefficients and aerodynamic moment coefficients,respectively.On the other hand,the unknown timevarying disturbance moments in the fast-loop system of the UAV are given by

The designed parameters of the proposed robust adaptive tracking control scheme are chosen as PPP1=[2α+0.5,2β+ 0.5,2µ+0.5]T,C1=diag{4,4,4},ρ1=0.4,γ1=0.5, k1=0.2,Γ1=diag{0.02,0.02,0.02},PPP2=[2p+0.5,2q+ 0.5,2r+0.5]T,C2=diag{2.5,2.5,2.5},ρ2=2.5,γ2=1.0, k2=0.5,C0=diag{5,5,5},andε0=0.02.

The simulation results are shown in Figs.1～8,where dot lines(with subscript“c”)represent the desired attitudes,and dash dot lines(with subscript“1”)stand for the responses without NDO or saturation compensation,and dash lines(with subscript“2”)represent the responses with NDO,and solid lines(with subscript“3”)stand for the responses with NDO and saturation compensation.

Under the proposed robustadaptive tracking controlscheme based on the backstepping approach,DSC and NDO,we can see that the system outputs follow the desired values in a satisfactory way in the presence of system uncertainty,unknown externaldisturbance,and inputsaturation from Figs.1～3.The compounded disturbance can be well tackled with NDO,and the oscillation phenomena is reduced.On the other hand,the controlinputs are presented in Figs.4～8.Itshould be noticed that the designed auxiliary system can make actuators drop outthe saturation nonlinearity gradually,eliminating the effect of input saturation.Based on above simulation results and stated analysis,the proposed robust adaptive tracking control strategy is valid for uncertain MIMO nonlinear systems with system uncertainty,unknown external disturbance,and input saturation.

Fig.1. Angle of attack.

Fig.2. Sideslip angle.

Fig.3. Roll angle.

Fig.4. Ailerons.

Fig.5. Elevator.

Fig.6.Rudder.

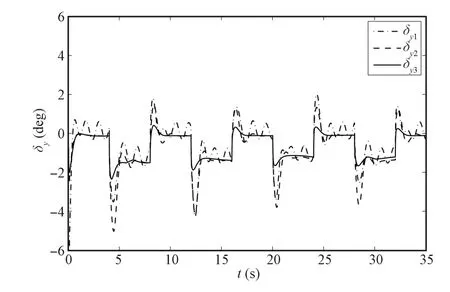
Fig.7. Lateral defection of the thrust vectoring control surface.

Fig.8. Longitudinal deflection of the thrust vectoring control surface.

VI.CONCLUSION

An effective robustadaptive tracking controlscheme is proposed for uncertain MIMO nonlinear systems in the presence ofsystem uncertainty,unknown externaldisturbance,and input saturation based on the backstepping technique and the NDO. To eliminate the

effectof inputsaturation,an auxiliary system is constructed. The dynamic surface method is employed to deal with the explosion of complexity in backstepping control.It is proved that all signals of the closed-loop system based on the proposed robust adaptive tracking control scheme are uniformly ultimately bounded through Lyapunov stability analysis.Finally,the developed control strategy is applied to the attitude tracking control of a UAV,and simulation results show that the proposed robust control scheme is effective.

REFERENCES

[1]Chen M,Jiang B,Wu Q X,Jiang C S.Robust control of near-space vehicles with input backslash-like hysteresis.Proceedings of the Institutior of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2013,227(8):635−644

[2]Ji Chen-Xin.Key technology and application of military unmanned aerial vehicles.Modern Defence Technology,2009,37(6):26−30(in Chinese)

[3]Wang Qin,Ye Yun-Qing.Application of unmanned aerial vehicle in navy.CommandInformationSystemandTechnology,2012,3(4):36−40 (in Chinese)

[4]Wang F,Cui J Q,Chen B M,Lee T H.A comprehensive UAV indoor navigation system based on vision optical flow and laser fastslam.Acta Automatic Sinica,2013,39(11):1889−1990

[5]Kang Y,Hedrick J K.Linear tracking for a fixed-wing UAV using nonlinear model predictive control.IEEE Transactions on Control Systems Technology,2009,17(5):1202−1210

[6]Dierks T,Jagannathan S.Output feedback control of a quadrotor UAV using neural networks.IEEE Transactions on Neural Networks,2010, 21(1):50−66

[7]Nodland D,Zargarzadeh H,Jagannathan S.Neural network-based optimal adaptive output feedback control of a helicopter UAV.IEEE Transactions on Neural Networks and Learning Systems,2013,24(7): 1061−1073

[8]Chen M,Mei R,Jiang B.Sliding mode control for a class of uncertain MIMO nonlinear systems with application to near-space vehicles.Mathematical Problems in Engineering,2013,DOI:10.1155/2013/180589

[9]Dydek Z T,Annaswamy A M,Lavretsky E.Adaptive control of quadrotor UAVs:a design trade study with flight evaluations.IEEE Transactionson Control Systems Technology,2013,21(4):1400−1406

[10]Chen W H,Ballance D J,Gawthrop P J,O'Reilly J.A nonlinear disturbance observer for robotic manipulators.IEEE Transactions on Industrial Electronics,2000,47(4):932−938

[11]Chen WH.Nonlinear disturbance observer-enhanced dynamic inversion control of missiles.Journal of Guidance,Control,and Dynamics,2003, 26(1):161−166

[12]Chen M,Chen W H.Sliding mode control for a class of uncertain nonlinear systems based on disturbance observer.International Journal of Adaptive Control and Signal Processing,2010,24(1):51−64

[13]Qian C S,Sun C Y,Huang Y Q,Mu C X,Zhang J M,Zhang R M. Design of flight control system for a hypersonic gliding vehicle based on nonlinear disturbance observer.In:Proceedings of the 10th IEEE International Conference on Controland Automation.Hangzhou,China: IEEE,2013.1573−1577

[14]Pu Ming,Wu Qing-Xian,Jiang Chang-Sheng,Cheng Lu.Application of adaptive second-order dynamic terminalsliding mode controlto near space vehicle.Journal of AerospacePower,2010,25(5):1169−1176(in Chinese)

[15]Guo Tao,Wang Ding-Lei,Wang Ai-Min.Adaptive backstepping control for constrained systems using nonlinear mapping.Acta Automatic Sinica,2013,39(9):1558−1563(in Chinese)

[16]CuiR X,Ren B B,Ge S S.Synchronised tracking controlofmulti-agent system with high-order dynamics.IETControl TheoryandApplications, 2012,6(5):603−614

[17]Wang H Q,Chen B,Lin C.Adaptive neuraltracking controlfora class of perturbed pure-feedback nonlinear systems.Nonlinear Dynamics,2013, 72(1−2):207−220

[18]Li T S,Li R H,Wang D.Adaptive neural control of nonlinear MIMO systems with unknown time delays.Neurocomputing,2012,78(1): 83−88

[19]Li Y M,Tong S C,Li T S.Adaptive fuzzy output feedback control of MIMO nonlinear uncertain systems with time-varying delays and unknown backlash-like hysteresis.Neurocomputing,2012,93:56−66

[20]Swaroop D,Hedrick J K,Yip P P,Gerdes J C.Dynamic surface controlfora class ofnonlinear systems.IEEETransactionsonAutomatic Control,2000,45(10):1893−1899

[21]Li Tie-Shan,Zou Zao-Jian,Luo Wei-Lin.DSC-backstepping based robust adaptive NN control for nonlinear systems.Acta Automatica Sinica,2008,34(11):1424−1430(in Chinese)

[22]Xu Y Y,Tong S C,Li Y M.Adaptive fuzzy fault-tolerant decentralized control for uncertain nonlinear large-scale systems based on dynamic surface controltechnique.Journalofthe FranklinInstitute,2014,351(1): 456−472

[23]Li T S,Zhang H Y,Yang X Y.DSC approach to robustadaptive fuzzy tracking control for strict-feedback nonlinear systems.In:Proceedings of the 5th International Conference on Fuzzy Systems and Knowledge Discovery.Jinan,China:IEEE,2008.70−74

[24]Jia Tao,Liu Jun,Qian Fu-Cai.Adaptive fuzzy dynamic surface control for a class of nonlinear systems with unknown time-delays.Acta Automatica Sinica,2011,37(1):83−91(in Chinese)

[25]Wen C Y,Zhou J,Liu Z T,Su H Y.Robust adaptive of uncertain nonlinear systems in the presence of input saturation and external disturbance.IEEE Transactions on Automatic Control,2011,56(7): 1672−1678

[26]Li Y M,Tong S C,Li T S.Directadaptive fuzzy backstepping controlof uncertain nonlinear systems in the presence of input saturation.Neural Computingand Applications,2013,23(5):1207−1216

[27]Zhou Yan-Long,Chen Mou.Robust control of nonlinear systems with input constraint based on disturbance observer.Journal of Nanjing Universityof Scienceand Technology,2014,38(1):40−47(in Chinese)

[28]Chen M,Ge S S,Ren B B.Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints.Automatica,2011, 47(3):452−465

[29]Chen M,Ge S S,How B V E.Robustadaptive neuralnetwork controlfor a class of uncertain MIMO nonlinear systems with inputnonlinearities. IEEE Transactions on Neural Networks,2010,21(5):796−812

[30]Chen M,Ge S S,Choo Y S.Neural network tracking control of ocean surface vessels with inputsaturation.In:Proceedings of the 2009 IEEE International Conference on Automation and Logistics.Shenyang, China:IEEE,2009.85−89

[31]Kurtz M J,Henson M A.Input-outputlinearizing controlof constrained nonlinear processes.Journal of Process Control,1997,7(1):3−17

[32]Kong Xiao-Bin,Liu Xiang-Jie.Continuous-time nonlinear model predictive control with input/output linearization.Control Theory and Applications,2012,29(2):217−224(in Chinese)

[33]Liu D R,Wang D,Yang X.An iterative adaptive dynamic programming algorithm for optimal control of unknown discrete-time nonlinear systems with constrained inputs.InformationSciences,2013,220:331−342

[34]Wang D,Liu D R,Zhao D B,Huang Y Z,Zhang D H.A neuralnetwork-based iterative GDHP approach forsolving a class of nonlinear optimal control problems with control constraints.Neural Computing and Applications,2013,22(2):219−227

[35]Chen M,Jiang B.Robust attitude control of near space vehicles with time-varying disturbances.International Journal of Control,Automation, and Systems,2013,11(1):182−187

[36]Polycarpou M M.Stable adaptive neural control scheme for nonlinear systems.IEEE Transactions on Automatic Control,1996,41(3): 447−451

[37]Tee K P,Ge S S.Control of fully actuated ocean surface vessels using a class of feedforward approximators.IEEE Transactions on Control Systems Technology,2006,14(4):750−756

[38]Pang J,Mei R,Chen M.Modeling and control for near space vehicles with oblique wing.In:Proceedings of the 10th World Congress on Intelligent Controland Automation.Beijing,China:IEEE,2012.1773−1778

Yanlong Zhou Master studentin the College of Automation Engineering,Nanjing University of Aeronautics and Astronautics.His research interests include flight control and nonlinear system control.

Mou Chen Professor in the College of Automation Engineering,Nanjing University of Aeronautics and Astronautics.His research interests include nonlinear system control,intelligent control,and flight control.Corresponding author of this paper.

Changsheng Jiang Professor in the College of Automation Engineering,Nanjing University of Aeronautics and Astronautics.His research interests include nonlinear system control,flight control.

t

September 26,2013;accepted March 24,2014.This work was supported by National Natural Science Foundation of China (61174102),Jiangsu Natural Science Foundation of China(SBK20130033), Aeronautical Science Foundation of China 20145152029)and Specialized Research Fund for the Doctoral Program of Higher Education (20133218110013).Recommended by Associate Editor Jie Chen

:Yanlong Zhou,Mou Chen,Changsheng Jiang.Robust tracking control of uncertain MIMO nonlinear systems with application to UAVs. IEEE/CAA Journal of AutomaticaSinica,2015,2(1):25−32

Yanlong Zhou,Mou Chen,and Changsheng Jiang are with the College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China(e-mail:zhouyanlong100@163.com; chenmou@nuaa.edu.cn;jiangcs@nuaa.edu.cn).