关于3种运动的瞬态过程问题赏析

郑 金

（凌源市职教中心 辽宁 朝阳 122500）

在电磁学中，暂态电路的充电和放电过程都属于瞬态过程，物理量随时间按指数规律变化.其微分方程及其通解都具有特定的形式.此外，对于物体的变速运动，由于受力特点不同，其瞬态过程将不同.

下面对有关物体从静止开始加速运动到最大速度的3种瞬态过程问题举例分析.

1 滑杆在恒定动力和安培力作用下的运动

对于物体在恒力F和线性阻力f＝kv共同作用下的加速直线运动过程，速度变化遵循一定的规律.

【例1】如图1所示，足够长的光滑水平导轨，相距l＝0.5m，左端接有电阻R＝1Ω.匀强磁场的磁感应强度为B＝2T，方向与轨道平面垂直，金属棒置于导轨上，质量为m＝200g，电阻为r＝0.5Ω.现让金属棒在水平恒力F＝2N 作用下由静止开始沿轨道运动.设金属棒始终在磁场中与轨道接触良好，导轨和导线的电阻均不计.对于金属棒从开始运动到速度最大的过程，求：

（1）金属棒发生的位移；

（2）通过电阻R 的电荷量；

（3）在电阻R 上产生的热量.

图1

解析：（1）金属棒切割磁感线产生的感应电动势为E＝Blv，则金属棒受到安培力为

由牛顿第二定律列微分方程为

即

由此可知稳定速度为

时间常数为

因初速度v0＝0，由瞬态过程的结论可得金属棒沿轨道下滑的速度为

由动量定理有Ft－ks＝mv，可得位移关系式为

（2）由动量定理有

可得通过金属棒的电荷量为

所以在电阻R 上产生的热量为

如果在题中给出的位移、电荷量或热量的某个数值小于上述计算结果，将导致题目中的数据不自洽.

2 潜艇在线性阻力作用下以恒定功率行驶

对于物体在线性阻力作用下以恒定功率加速直线运动的过程，速度变化遵循一定的规律.

【例2】有“潜艇之王”之称的美国“俄亥俄”级潜艇，在水下行驶时的质量为2万吨，行驶中受阻力f＝kv，其中k＝1.8×105N·s／m，当其以P＝4.0×104kW 的恒定功率在水下行驶时，求：

（1）最大速度；

（2）启动多长时间达到最大速度的一半？

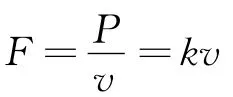
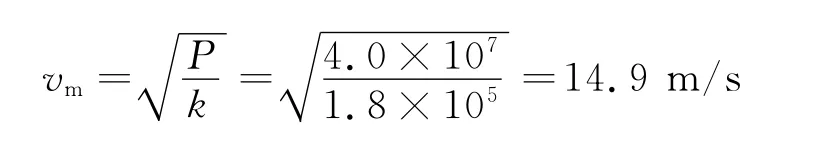
分离变量得

即

由此得

3 汽车在恒定阻力作用下以恒定功率行驶

对于物体在恒定阻力作用下以恒定功率加速直线运动的过程，速度变化遵循一定的规律.

【例3】已知汽车的额定功率为P，质量为m，运动过程中受到恒定阻力为f，汽车运动的初速度为v0，求汽车达到最大速度所需的时间是多少？

设

则

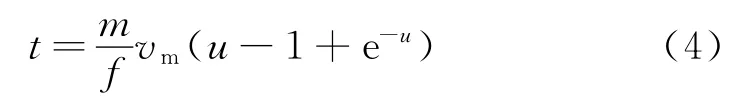
由式（3）得

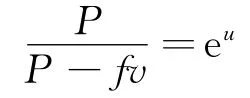
则

代入式（4）并整理得

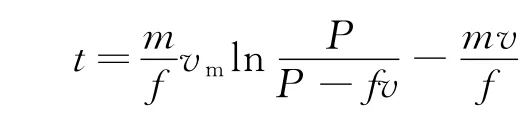
即为

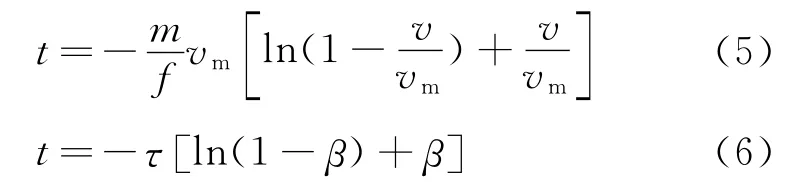
由（3）式可知，当u＝5时，速度v＝0.993vm，此时可认为汽车达到最大速度，则由（4）式可知汽车从静止到速度最大过程所经历的时间为

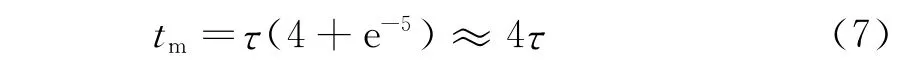
如果初速度为v0，则由静止加速到v0经历的时间为

所以汽车从初速度为v0加速到最大速度所需的时间为t＝tm－t0，即为

式（6）是不同速度所对应的时间，式（9）是物体达到最大速度所经历的时间.

【例4】（2009年高考上海物理试卷第20题）质量为5×103kg的汽车在t＝0时刻速度v0＝10m／s，随后以P＝6×104W 的额定功率沿平直公路继续前进，经72s达到最大速度，设汽车受恒定阻力，其大小为2.5×103N.求：

（1）汽车的最大速度vm；

（2）汽车在72s内经过的路程s.

分析：最大速度为

将数据代入式（9）得时间为

此时汽车的速度为v＝0.993vm≈23.83m／s，非常接近最大速度了.

可见原题中的数据t＝72s是不合理的，或者说是不自洽的.

对于例题1，可直接利用瞬态过程的结论进行解答，称为指数瞬态过程；对于例题2和3，则需先对微分方程变换形式，再利用瞬态过程的结论进行解答，可称为另类瞬态过程.需通过数学变换，使某一变量与指数瞬态过程发生联系，从而利用瞬态过程的结论，化繁为简.

有趣的是，对于物体由静止开始加速运动的瞬态过程，达到最大速度所经历的时间都与“满速比”β有关.

当动力恒定，阻力为线性力时

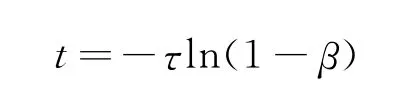
当动力功率恒定，阻力为线性力时

当动力功率恒定，阻力为恒力时

对应的时间常数分别为

综上可见，瞬态过程形式多样.解答瞬态过程问题的关键是列出变量的一阶常系数线性微分方程，再利用瞬态过程的结论直接写出通解，可避免数学积分过程.瞬态过程的结论不仅能巧妙解题，而且还可用来拟题，或者判断题目中的数据是否自洽以及检验常规解法所得结果是否正确.

1 朱佩明.物理问题的规定性与习题命制的误区.物理教学，2009（1）：42

2 詹国荣.恒功率启动运行物体的速度变化规律.物理教学，2012（5）：52

3 赵曰峰，赵林明，宋辉武.谈汽车以额定功率启动达到最大速度的时间.物理教师，2014（5）：58