复现风力机五自由度载荷的加载控制方法
殷秀兴,顾亚京,林勇刚,叶杭冶,李 伟
(1.浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州310027;2.风力发电系统国家重点实验室,浙江 杭州310012)
为满足载荷测试要求,研究加载控制方案并设计开发相应的试验平台成为当务之急.目前,较常见的方案为单自由度电机拖动加载方式.该方式采用可控力矩电机来模拟旋转叶轮的扭矩和速度等特性,对由传动轴,齿轮箱和发电机等构成的被试件施加风力扭矩.Hansen等[1]开发的一套兆瓦级风电齿轮箱加载平台即是采用背靠背式的拖动加载方式,由变速原动机和传动比可选的减速箱模拟叶轮,由增速齿轮箱,传动链和可控力矩发电机构成被试件.然而,拖动加载方式虽然能模拟风力扭矩,但并不能体现叶轮及其惯量的影响,也不能模拟由叶轮传递而来的多自由度载荷,因而并不能有效地实现真实的载荷测试.
模拟机组多自由度载荷的非扭矩加载方案除采用拖动电机来模拟叶轮扭矩特性外,还采用多个液压缸的出力来合成多自由度载荷,通过控制各液压缸的施力方向和大小来模拟载荷的变化.Dempsey等[2]开发的一套2.5 MW 的加力装置,即采用了非扭矩作动器,将各液压缸的出力合成以再现机组在典型工况的推力,弯矩和剪切力.严伟鑫等[3-4]研究了一种动态非扭矩加载器,采用数个铅直和水平液压缸以及连杆实现五自由度力和弯矩的再现控制.上述非扭矩加载方案虽然可以再现机组五自由度载荷,但大多忽视了叶轮惯性的影响,也没有详细地给出加载控制的策略和模型,仅仅停留于几何外形的描述.
本文提出一种复现风力机五自由度载荷加载方案.将叶轮及其组件等效成加载盘,并在该盘的轴向和径向表面均匀地设置一组可控加载器,利用各加载器的输出力来合成所需载荷.相比于现有的加载方式,该方案不仅能复现五自由度载荷,而且考虑了叶轮惯量等影响,且方案简洁清晰,易于实现,能够更好地模拟机组实际运行的载荷状况,有利于进行高效的载荷测试.
1 实现原理
1.1 设计方案
如图1所示,将机组载荷的承载部件,如叶轮,轮毂等构件等效成为一圆盘,作为加载的力和弯矩的作用对象,称该圆盘为加载盘.

图1 加载系统设计原理Fig.1 Design scheme of loading system
在加载盘的两侧面内沿轴向分别均匀对称地设置8个加载器,在加载盘圆周上沿径向均匀对称地设置8个加载器,这样轴向和径向分别有16和8个加载器.将齿轮箱、发电机及相关电气部件作为被试件.变频电动机通过传动轴拖动加载盘以低速轴转速旋转,以模拟真实风力机运行工况.传动轴带动被试件和发电机旋转,发电机电能最终回馈到电网.
按相应的加载策略控制各轴向和径向加载器输出力的大小方向来合成五自由度载荷,并因而对被试件产生影响.由于加载盘与传动轴相连并随之做旋转运动,因而液压缸活塞杆需通过静压轴承与加载盘作浮动连接,以便于液压缸的固定和加载盘的正常运转.
为保证较高的载荷复现精度,加载系统的闭环频率响应的带宽应当大于机组旋转的三阶谐波频率.同时,加载系统液压油源的压力和流量应能保证并满足最大加载力和加载速度的需要.
1.2 加载策略
如图2所示,以等效获得的加载盘为受力分析的对象,以其质心为原点建立加载坐标系[5]x-y-z.其中x 轴沿主轴轴线并指向下风向,z 轴在叶轮或加载盘旋转面内并与水平面垂直,y 轴在叶轮旋转平面内并与x,z轴构成右手坐标系.通过坐标等效变换的方式[6],将桨叶和塔架等坐标系内所分析的风力机各部分动态载荷[7]映射转换到加载坐标系中并合成,可获得机组五自由度载荷模型为Fx、Fy、Fz、My、Mz.如图2所示、Fy、Fz分别表示叶轮,轮毂等部件受到的轴向和径向的力载荷,My、Mz表示挥舞,摆振等弯矩载荷.而Mx为拖动叶轮的扭矩载荷,该载荷由电机拖动并独立施加,此处暂不考虑.实际加载时,可通过实测或软件获得五自由度载荷的参考波形数据.

图2 加载盘受力分析Fig.2 Force analysis of loading disc
载荷复现的首要工作便是将五自由度载荷分解到各相应的加载器上,以得到各加载器需要再现的参考加载力.分别将轴向和径向上对称分布的对置加载器的合力视为需求解的单位加载力矢量.这样,加载盘共作用有12个单位加载力矢量,而这些力矢量再合成可获得五自由度载荷,即仅有5个约束方程,却有12个未知量,为静不定方程组.为解决该问题,提出一种基于虚拟载荷的12自由度加载策略,增设7自由度虚拟载荷,构成12个载荷约束方程,以获得确定的加载力矢量.
如图2所示,定义由沿X 轴正向和逆向合成的轴向单位加载力矢量为Fai=Fari-Fali,其中i=1,…,8,Fari和Fali分别为右轴向和左轴向的加载力矢量;定义径向单位加载力矢量为Frj=Fruj-Frdj,其中j=1,…,4,各单个加载器的输出力均为正值,Fruj和Frdj分别为径向向上和向下的加载力矢量.
据此,可获得单个加载器的参考加载力为
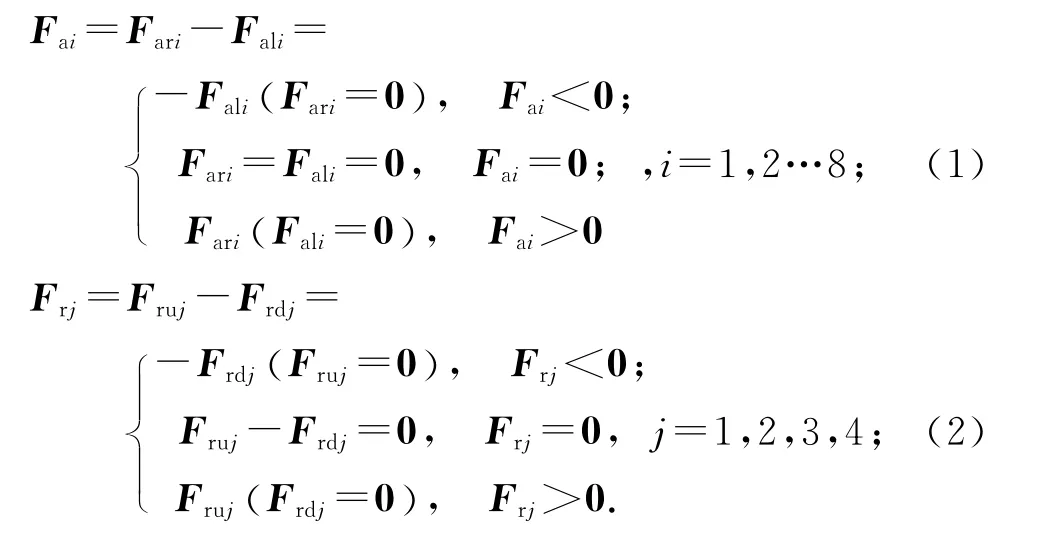
加载力约束方程组为

式中:r为轴向加载器分布圆半径,Fai为轴向单位加载力矢量,Frj为径向单位加载力矢量.
定义七自由度虚拟载荷为

令

联立式(3-4),可得矩阵表达式为
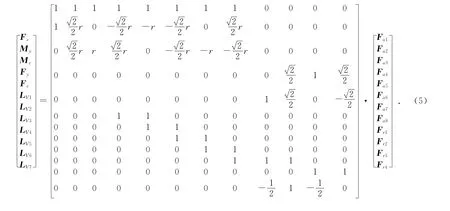
式(5)又可写成

式中:
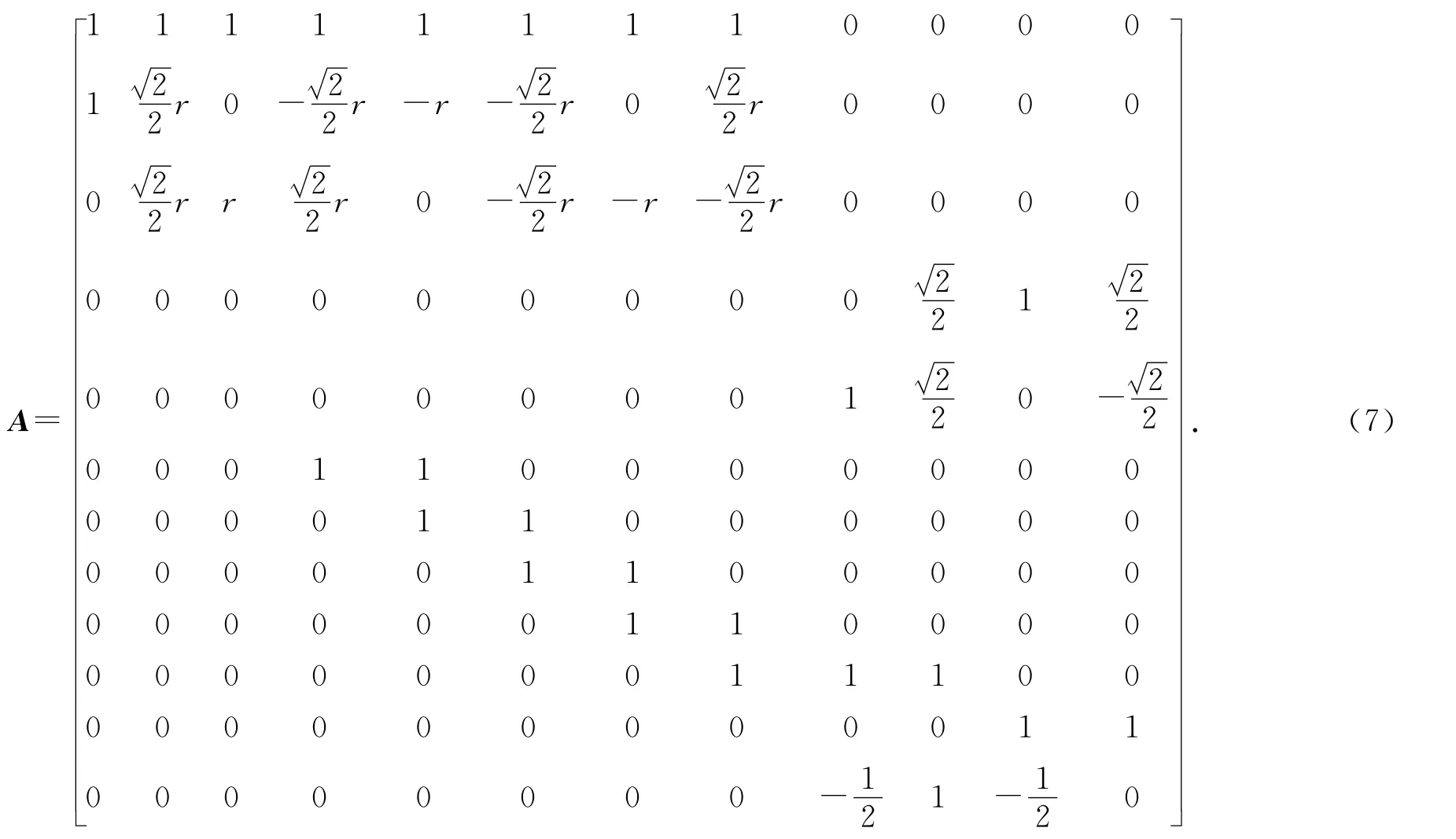
在输入载荷数据时,7个虚拟载荷的给定值均为零值,其余均输入有效值.具体解算时,可先根据式(5)~(6)获得轴向和径向的单位加载力矢量,再根据式(1)~(2)和加载力的正负情况选择对应方向的加载器来实现该力,而根据式(6),经矩阵分解获得的力即作为该加载器的目标加载力.
2 数学模型
各加载器均采用零开口四边滑阀控制单出杆液压缸的形式,采用输出力控制方式.鉴于各加载器仅安装位置不同,可取轴向的单加载器进行建模分析.
如图3所示,忽略静压轴承的油膜黏性,将其支承油膜等效为负载弹簧[8],并将弹簧刚度K 与液压缸活塞杆位移之积视为加载力.据此,建立力控制系统的非线性模型[9].
动态力平衡方程为
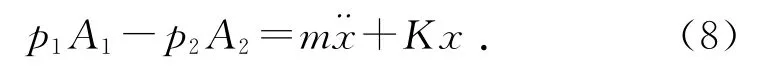
液压缸流量连续性方程为

式中:x 为活塞杆位移,m 为活塞杆端部等效质量,K 为油膜弹簧刚度,p1、p2分别为液压缸两腔压力,A1,A2分别为液压缸两腔有效面积,qV1、qV2分别为流入,流出液压缸两腔的流量,Cip为液压缸内泄漏系数,V10为无杆腔的初始容积,V20为有杆腔的初始容积,βe 为油液的体积模量.

图3 加载原理模型Fig.3 Schematic of loading system
定义符号函数

加载器流量方程为

式中:Cd为阀口流量系数,xV为阀芯位移,ω1、ω2分别为阀进油口和回油口面积梯度,ρ为油液密度,ps为供油压力,p0为回油压力.
鉴于符号函数(11)在原点处不可导,影响控制器的设计和实现,可采用双极性连续可微的sigmoid函数代替之,即
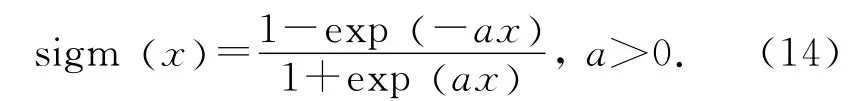
式中:a为正常数.则有

这样,可通过选择合适的a值,以较好地逼近上述符号函数.
将比例阀视为二阶振荡环节:

式中:ωn为比例阀的固有频率,ξn 为比例阀的阻尼比,u为比例阀的控制电压,即控制量.
加载力方程为
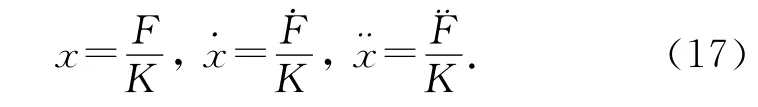
式 中:F 为 加 载 力.
定义状态变量为
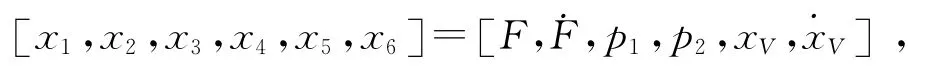
则系统非线性状态空间模型为
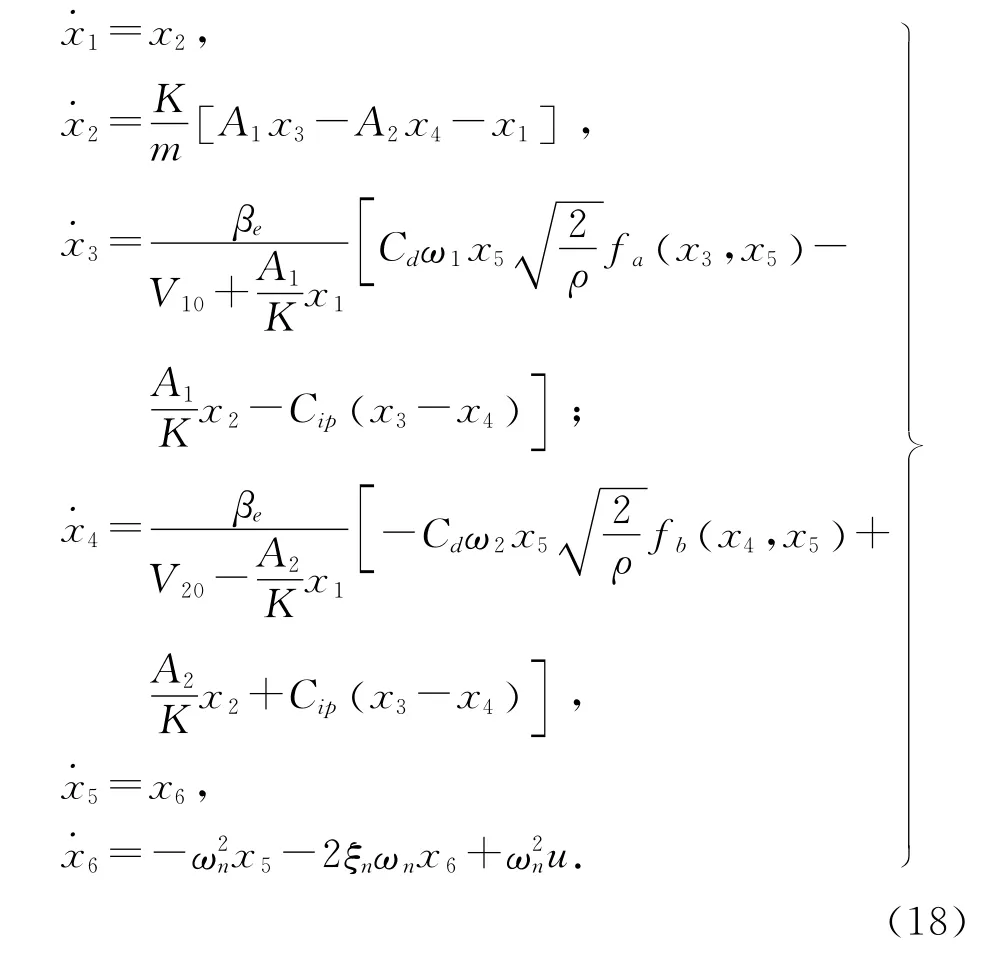
式中:
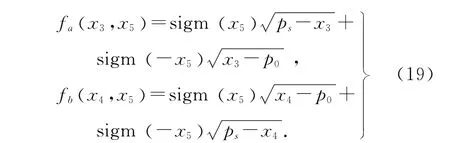
定义状态变量
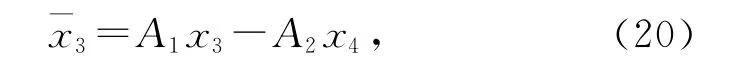
则有
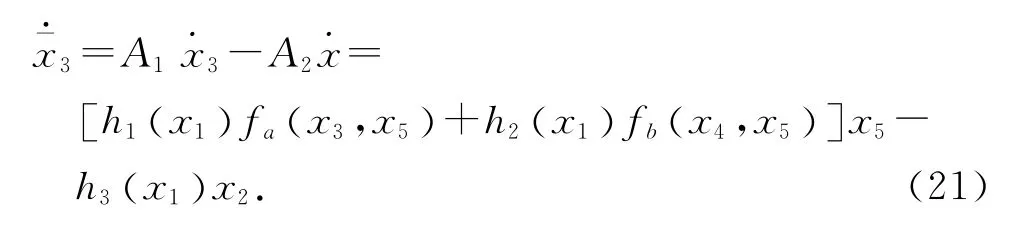
联立式(18)~(21),可得系统状态空间模型的严格参数反馈形式为
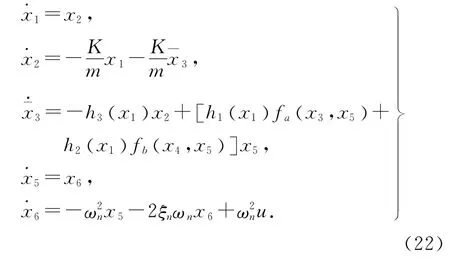
式中:

方程(18)~(22)给出了具有普遍意义的精确的加载力控制模型,在该模型中,风况载荷是以给定的加载力的形式作为控制系统的跟踪目标或者参考指令值而输入到系统中的,而非以风力干扰的形式直接作用于加载盘上,因而控制模型不会因风况变化而改变.即该模型仅取决于系统本身的液压流体的物理特性和阀控液压缸的实际结构.
该控制系统采用闭环反馈控制方式,设计为伺服随动控制结构,在其闭环频宽范围内,能够较好地复现复杂的风况载荷,可适合各风况.
3 控制器设计
针对系统模型非线性较强以及加载力随机性和幅度变化较大的特点,设计加载力反演控制器[10],以获得较快的响应性和良好的力跟踪性能.采用设置虚拟量和逐步递推方式获得控制量,采用Lyapunov函数推证稳定性.
1)定义加载力偏差e1和Lyapunov函数V1:

式中:Fr为参考加载力,该力为根据式(1)~(7)分解而获得的加载器的目标加载力之一,e1为定义加载力偏差,V1为Lyapunov函数.
考虑式(22),式(24)函数V1微分为
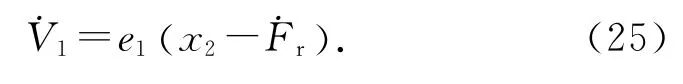
若选择

式中:xd2为x2的目标值,k1(k1>0)为常数.
但x2真实值由实际加载过程决定,该值与其目标值间尚有偏差.
将式(26)代入式(25),则有
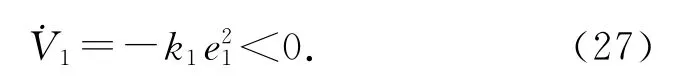
2)定义Lyapunov函数为
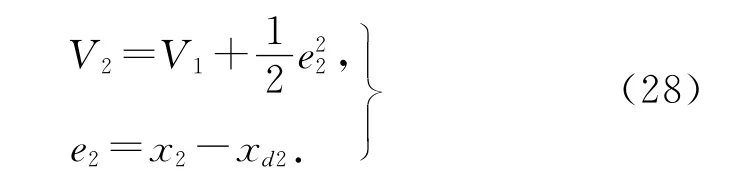
考虑式(22),式(28)函数V2微分为

若选择
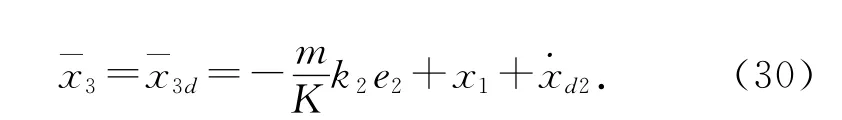
将式(30)代入式(29),则有

3)定义Lyapunov函数为

考虑式(22),上式函数V3微分为

若选择

式中:xd5为x5的目标值,k3(k3>0)为常数.
但x5真实值由实际加载过程决定,该值与其目标值间尚有偏差.
将式(34)代入式(33),则有

4)定义Lyapunov函数为
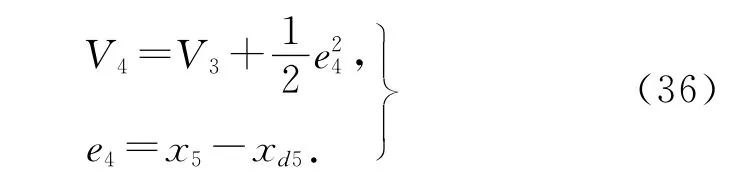
考虑式(22),上式函数V4微分为
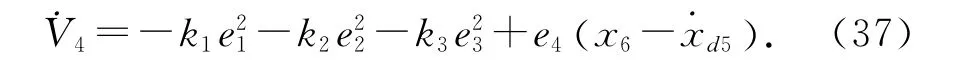
若选择

式中:xd6为x6的目标值,k4(k4>0)为常数.
但x6真实值由实际加载过程决定,该值与其目标值间尚有偏差.
将式(38)代入式(37),则有
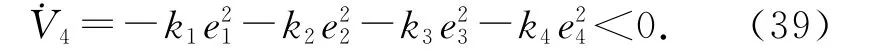
5)定义Lyapunov函数为
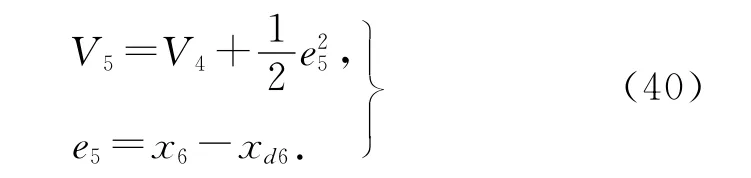
考虑式(22),上式函数V5微分为

选择常数k5(k5>0),并设定控制量u为

联立式(41)~(42),则函数V5微分为

根据式(24)~(43),当k1,k2,k3,k4,k5>0时,˙V1,˙V2,˙V3,˙V4,˙V5均 负 定,根 据Lyapunov稳 定性判据[11],系统大范围渐近稳定,各状态变量将趋近于其目标值,实际加载力最终将趋于其给定值.
式(42)描述的控制律建立在系统精确模型的基础上,为一般性的加载力反演控制律.控制量中以系统常量和线性运算居多,复杂性主要存在于xd5的导数中的一些非线性运算和阀芯速度测量,整体上复杂度并不高.实际应用时,需要确保各个状态变量和参考加载力的微分存在,且不能为零或无穷.同时,各状态量和液压参数要根据加载系统实际情况进行取值,均有一定的取值范围,且不能突变.跟踪误差和Lyapunov函数须在有限的时间内收敛.
4 结果与分析
系统能够较好地复现五自由度载荷的关键在于单个加载力系统的快速响应性以及对给定力值的精确跟踪性能.因而,可首先对单个加载力系统进行研究,对比分析采用不同控制方法时,系统的响应及跟踪性能.
根据式(8)~(23)在simulink中建立力加载模型.其中,系统压力为10 MPa,最大流量设为12L/min,最大加载力1.5kN.分别采用比例积分(proportional-integral,PI)控制器和反演控制器进行加载力控制.PI参数分别为0.018和0.004,采用仿真试凑方法整定.反演控制模型根据式(24)~(43)建立,采用仿真试凑的方法整定常数k1~k5.常数k1对系统的响应速度和偏差大小影响较大,可选取较大的正值,而其余常数均选为1 即可.分别输入阶跃,正弦和随机载荷信号,分别分析系统响应情况.
在单个加载器施力控制分析基础上,研究加载系统整体对于五自由度载荷的复现跟踪情况.根据式(1)~(7)所述的加载策略,建立系统整体的加载模型,采用矩阵运算和切换函数实现加载力的分解或合成.采用Bladed软件基于100kW 风力机的实际数据计算获得的载荷谱作为五自由度载荷参考值.其中,最大合成加载力为20kN,最大加载弯矩值为40kN·m.
4.1 单缸加载力特性
如图4所示,在PI控制作用下,系统调整时间基本为0.6s,最大超调量为20%左右,有约5%的稳态误差;而采用反演控制时,调整时间降为0.4s,最大超调量降为6%,稳态误差基本为零.这样,相比于PI控制,反演控制对阶跃加载力的跟踪精度较高.

图4 加载力阶跃响应Fig.4 Response to square input
如图5所示,当输入5 Hz正弦载荷信号时,PI控制的加载力有10%的相位滞后,反演控制时加载力滞后约为2%.如图6所示,当输入10 Hz正弦载荷信号时,PI控制的加载力有50%的相位滞后,反演控制的加载力滞后仍维持在5%以内.这样,相比于PI控制,反演控制对于正弦加载力的滞后较小,力跟踪精度较高.对比图5和6 亦可知,当采用PI控制时,输入信号频率越高,力跟踪精度有所降低.
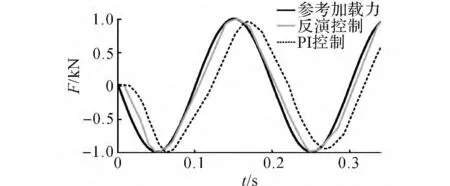
图5 5Hz正弦输入响应Fig.5 Response to 5Hz sinusoidal input

图6 10Hz正弦输入响应Fig.6 Response to 10Hz sinusoidal input
如图7和8 所示,当输入随机信号时,PI控制的加载力稳态跟踪误差为0.05~0.18kN,最大误差出现于6~8s;而采用反演控制的加载力稳态误差基本维持在0.05kN 以内,最大误差出现在6s时,最大值为0.04kN 左右.这样,相比于PI控制,反演控制具有较高地随机加载力稳态跟踪精度.
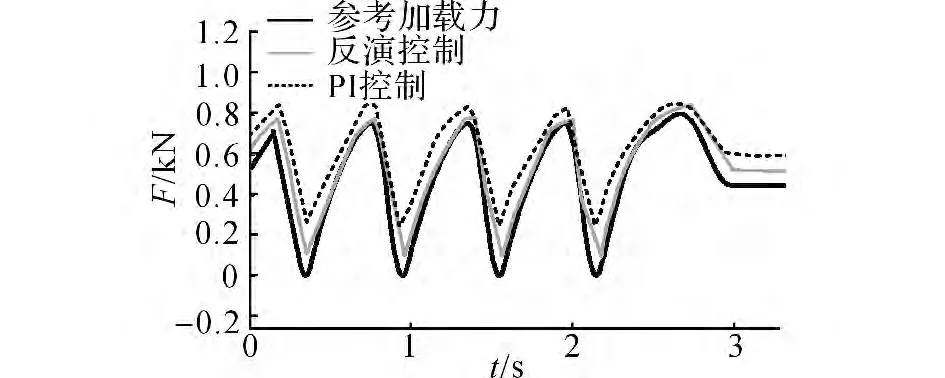
图7 随机载荷输入响应Fig.7 Response to random loading input
4.2 五自由度载荷复现结果
如图9(a)所示,PI控制的Fx载荷跟踪偏差介于20%~40%,最大偏差出现于180s附近,约为43%;采用反演控制的力跟踪偏差介于0~20%,在0~35s和50~80s时间段内误差较大,约为20%左右,其余时间段内,基本维持在2%以内.说明,相比于PI控制,反演控制具有较好的Fx载荷复现精度.
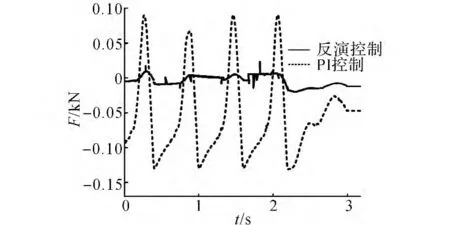
图8 随机载荷响应误差Fig.8 Response error to random loading input

图9 五自由度载荷复现结果Fig.9 Reproduced five-degree-of-freedom loads
据图9(b)可知,PI控制的Fy载荷复现误差介于5%~20%,最大偏差出现于60s 附近,约为20%;采用反演控制的力跟踪偏差最大值约为20%,出现在5 和35s时,其余时刻误差均小于5%.说明,相比于PI控制,除起始时段外,反演控制具有较好的Fy载荷跟踪精度.
由图9(c)可知,PI控制的Fz载荷跟踪误差在5%~50%之间,最大误差出现在250s附近;反演控制的载荷跟踪偏差介于0%~25%之间,在35s附近有最大值,其余时段内均低于5%.可看出,反演控制的载荷复现误差基本小于PI控制,说明反演控制的Fz载荷复现精度相对较高.
根据图9(d)可知,PI控制的My弯矩跟踪误差介于10%~25%,最大误差出现在135s附近;反演控制的载荷跟踪误差在起始时段内较大,在43s附近达到最大的25%左右,但从60s开始跟踪误差基本维持在5%以内.说明,相比于PI控制,反演控制在较长时段内对My弯矩复现精度较高.
如图9(e)可知,PI控制的Mz弯矩跟踪误差介于5%至25%,最大误差出现于143和280s附近;反演控制的载荷跟踪误差在100~150s时段内较大,最大达20%左右,其余时段内均小于5%.说明,相对于PI控制,反演控制在整体时段内对Mz弯矩复现精度较高.
5 结 论
(1)复现风力机五自由度载荷的方案具有合理性,加载策略容易编程实现,并能由此获得单个加载器上需复现的参考加载力.
(2)单个加载器可按照非线性电液力控制系统进行建模分析,静压支承可用负载弹簧等效.
(3)可通过逐步递推和设置虚拟目标值的方式设计非线性反演控制器.
(4)相比于PI控制,反演控制的加载力系统对输入信号跟踪精度较高,并具有较高的五自由度载荷复现精度.
(5)将简化并获得更易于实现的反演控制算法,对整个加载系统建模分析并进行实验研究.
(6)考虑到风况载荷的非对称,不均匀及多变等复杂特性,将进一步考虑并研究如何精简加载器来实现较高精度的载荷复现,并将深入探讨具有针对性的灵活组合方式的加载控制方案.
(
):
[1]HELSEN J,VANHOLLEBEKE F,DE CONINCK F,et al.Insights in wind turbine drive train dynamics gathered by validating advanced models on a newly developed 13.2 MW dynamically controlled test-rig [J].Mechatronics,2011,21(4):737-752.
[2]DEMPSEY P J,Sheng S.Investigation of data fusion applied to health monitoring of wind turbine drivetrain components[J].Wind Energy,2013,16(4):479-489.
[3]严伟鑫.风电传动链非扭矩载荷技术研究[D].杭州:浙江大学,2012.Yan Wei-xin.Research on the technology of non-torque loading system for wind turbine drivetrain,Master’s thesis of Zhejiang University[D].Hangzhou:Zhejiang,2012.
[4]严伟鑫,周晓军等.一种风力发电机组试验台模拟加载装置:中国,ZL201120095778.7.[P]:2008-10-1.Yan wei-xin,Zhou Xiao-jun,etc.A wind turbine load-ing simulation device[P]:China,ZL201120095778.7.2008-10-1.
[5]BURTON T,JENKINS N,SHPRPE D,et al.Wind energy handbook [M].[S.l]:John Wiley & Sons,2011.
[6]MARTIN O L.Hansen.Aerodynamics of wind turbines[M].Second edition.Routledge:[s.n.]2013:71-81.
[7]赵丹平,徐宝清.风力机设计理论及方法[M].北京:北京大学出版社,2012:46-61.
[8]虞烈,刘恒著.轴承-转子系统动力学[M].西安:西安交通大学出版社,2001:67-128.
[9]李连升,刘绍球.液压伺服理论与实践[M].北京:国防工业出版社,1990:128-169.
[10]胡云安著.非线性系统鲁棒自适应反演控制[M].北京:电子工业出版社,2010:18-88.
[11]段魁臣编著.稳定性基本理论与Lyapunov函数构造[M].乌鲁木齐:新疆大学出版社,1990:16-28.

