结构可靠度分析中的混合模拟法及应用

蒋正文，万 水，李明鸿，马 磊

（东南大学 交通学院，江苏 南京210096）

对实际工程进行结构可靠度分析，可以发现大部分结构具有随机变量多、隐式功能函数等特点［1］.针对显式结构功能函数的数值积分法、改进一次二阶矩法［2］等传统方法显然难以解决以上问题.Monte-Carlo法在处理隐式功能函数的结构可靠度分析上具有相当的优势［3-8］.当结构失效概率小于10-3时，Monte-Carlo法的计算效率较低.采用传统响应面法对隐式功能函数的实际工程进行结构可靠度分析较理想.为了提高响应面法的计算精度及效率，许多学者针对响应面函数的形状［9-11］、试验取样点的选取［2，12-15］等对响应面法进行改进.此外，吕大刚等［16-17］利用均匀设计表选取响应面函数的取样点，提出均匀设计响应面法，并将其运用于钢框架结构的抗震可靠度分析.金伟良等［2，18］提出基于支持向量机、最小二乘向量机的改进响应面法.Liu等［19］基于均匀设计法和双加权回归分析法对响应面法进行改进.赵威等［20］结合均匀设计法与偏最小二乘法来拟合响应面函数.基于人工神经网络的可靠度分析方法能够较好地解决隐式功能函数的结构可靠度问题［21-23］.当实际工程结构的随机变量较多时，采用Monte-Carlo法、响应面法、人工神经网络算法及其改进算法均具有一定的局限性.

本文结合LHS 法与均匀设计响应面法，提出基于拉丁抽样均匀设计的混合模拟法（hybrid simulation method based on Latin hypercube sampling and uniform design response surface method，LUH）.该方法为具有多维随机变量、隐式功能函数等特点的复杂结构可靠度问题提供了一条新的解决途径.LUH 利用LHS法剔除不灵敏的随机变量的影响；然后运用均匀设计法选取响应面函数的试验点，结合JC法（国际安全联合委员会（JCSS）推荐的一次二阶矩法）计算结构失效概率，并拟合出功能函数方程.本文将LUH 法应用于2个经典可靠算例中，并将其计算精度、效率与其他经典方法进行对比分析.最后，将该方法运用于一座已建成的三跨连续刚构桥正常使用极限状态下的可靠度分析中.

1 基本原理

1.1 拉丁超立方抽样法

LHS法是一种多维分层抽样方法，基本思想如下：将每一个随机输入变量Xi的分布函数域在概率上N 等分为（k＝1，2，…，N ），对每个子区间进行独立等概率抽样，在每一次确定性计算分析中严格保证在每一子区间抽样一次［3-4］.为了保证抽取的随机数属于各子区间，第i个子区间内的随机数Vi须满足以下条件：

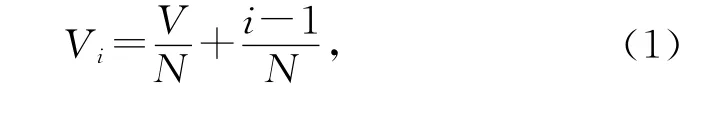
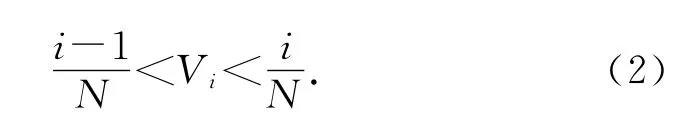
式中：i＝1，2，…，N；Vi为第i个子区间的随机数；V为［0 ，1］ 区间均匀分布的随机数.

对n 维随机变量Xi（i＝1，2，…，n）进行LHS抽样设计包括以下2个步骤［4］.

2）对每个随机变量Xi提取一个样本代表X并按照随机编号排列，对所有随机变量的样本都按照随机编号进行排列，从而形成N 个随机排列.每个排列均包含全部随机变量的一个样本代表.例如2 个随机变量10 次模拟的LHS 抽样设计如图1所示.

LHS抽样法具有抽样记忆功能，可以避免直接抽样法数据点集中而导致仿真循环重复的问题.它在抽样过程中强制抽样点必须离散分布在整个抽样空间.当随机输入变量的个数n 较大时，采用LHS法能够极大地减少抽样次数，且能够达到直接抽样法的同等精度.

图1 2个随机变量10次模拟的LHS法抽样数据Fig.1 Latin hypercube sampling table for two variables and ten runs

1.2 均匀设计响应面法

均匀设计方法是由我国数学家王元和方开泰于1978年提出的［24］.与具有均匀分散、整齐可比两大特点的正交设计方法相比，均匀设计只考虑试验取样点在试验范围内均匀散布.

对于多因素、多水平试验设计，均匀设计是一种对模型的变化有一定稳健性的方法.假如须对s个因素进行试验设计，设x1，x2，…，xs的试验区域为Cs＝［0，1］s，回归模型为

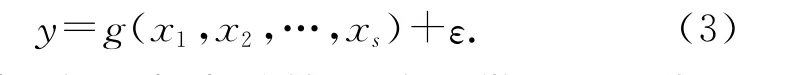
式中：g 为某已知函数类（例如二次可微），但具体形式未知；ε为随机误差.

通过试验估计响应在试验区域Cs上的平均值，即

由于试验误差Avg（ε）在Cs上的平均值接近于0，则

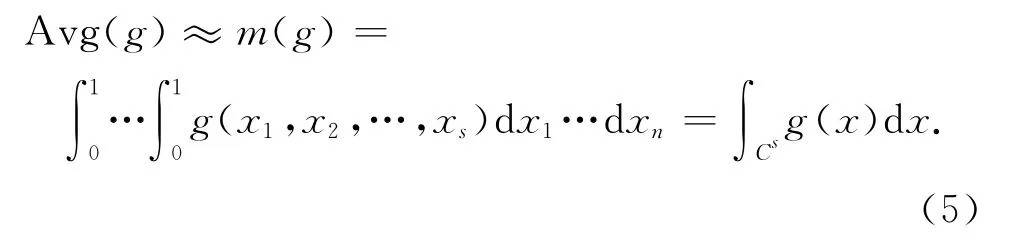
若 在Cs上 做n 次 试 验， 试 验 点 为 Pn＝｛xk＝ （xk1，xk2，…，xks），k＝1，2，…，n｝ ，则函数g 在n 个试验点上的平均值为

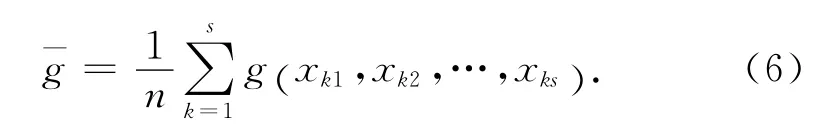
采用式（6）估计m（g） ，估计值引起的误差可由Koksma-Hlawka不等式表示为

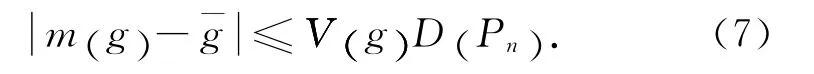
式中：V（g） 为函数g 在试验区域Cs上的全变差；D （Pn）为试验点集Pn在Cs上的偏差，它是度量Pn在Cs上散布均匀的测度.在试验设计时，应当选用使D （Pn）极小的试验点集，这是均匀设计的核心要求之一.

在数论方法中，最普遍采用L2-偏差来计算偏差D （Pn）.Warnock在1972年推导出其表达式［24］为

设计均匀设计表是一个优化偏差D （Pn）的过程，目前构造均匀设计表主要有好格子点法、拉丁方法、数值优化法等方法［16］.

吕大刚等［16-17］运用均匀设计法选取响应面函数的取样点，提出均匀设计响应面法，该方法具有较好的计算精度.Liu等［19-20，22-23］对均匀设计响应面 进行改进，均取得了较好的效果.

2 基于拉丁抽样均匀设计的混合模拟法及其实现

2.1 基于拉丁抽样均匀设计的混合模拟法

本文将LHS 法与均匀设计响应面法相结合，提出一种基于拉丁抽样均匀设计的混合模拟法.该方法综合了LHS 法和均匀设计响应面法的优点，使两者互为补充，其较Monte-Carlo法可以节省大量的计算时间.此外，混合模拟法通过对随机输入变量的可靠性灵敏度因子的分析，忽略灵敏度较低的随机输入变量的影响，减少了随机输入变量的数目，从而可以减少均匀设计响应面法循环的次数、提高计算效率，且计算精度较高.混合模拟法的流程如图2所示.

基于拉丁抽样均匀设计的混合模拟法的基本步骤如下.

1）对结构进行200～1 000次LHS抽样，计算各随机输入变量的可靠性灵敏度因子.

假如结构中存在n个服从一定分布的随机变量x1，x2，，…，xn，联 合 概 率 密 度 分 布 函 数 为fx（x1，x2，…，xn），结 构 极 限 状 态 函 数 为G （x1，x2，…，xn）：G （x1，x2，…，xn）＞0表示结构安全；G （x1，x2，…，xn）＜0 表 示 结 构 失 效；G （x1，x2，…，xn）＝0表示结构处于临界状态.

结构失效概率为

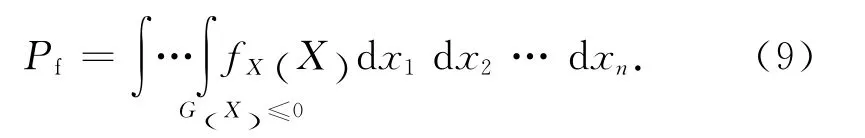
式中：X 为由变量x1，x2，…，xn表示的随机变量矢量.

设各随机变量的平均值、均方差的一般表达式为μxi、σxi，具体数值为，则各随机变量xi对结构失效的灵敏度为各随机变量的灵敏度因子为

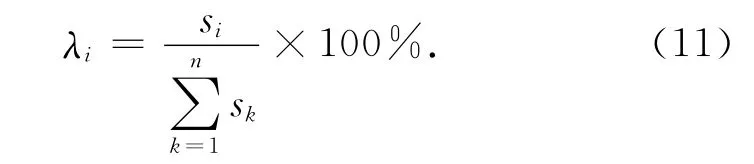
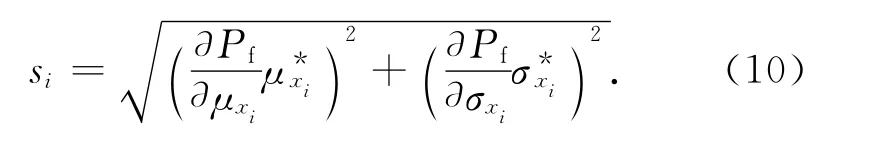
图2 基于拉丁抽样均匀设计的混合模拟法流程图Fig.2 Flow chart of LUH method

由于Pf通常不能由关于μxi、σxi的函数显式表达，张伟［25］提出采用下式近似计算灵敏度：

式中：PΔμxi为以μxi＋Δμxi替代μxi、而其他随机变量不变时的结构失效概率，PΔσxi为以σxi＋Δσxi替代σxi、而其他随机变量不变时的结构失效概率，Pf为以平均值、均方差计算出的结构失效概率.

2）将计算所得的可靠性灵敏度因子按其大小进行排序，将灵敏度较高的输入变量继续作为随机变量考虑，灵敏度较低的随机输入变量按确定性变量考虑.通常取2.5% 为临界值，当灵敏度因子≥2.5% 时认为灵敏度较高，当灵敏度因子＜2.5%时认为灵敏度较低［25-26］.

3）选取能够体现真实极限状态方程主要特点的响应面函数形式.通常选取不考虑交叉项的二次多项式为响应面函数：

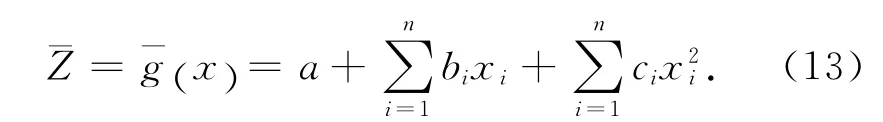
式中：a、bi、ci为回归系数.

7）由于式（13）中有2n＋1个回归系数，利用步骤6）中所得的2n＋1个结构响应，可以求解a、bi、ci（i＝1，2，…，n） ，从而确定均匀设计响应面函数，即为极限状态方程.

8）利用JC法求解显式化功能函数的可靠度指标β（k）以及设计验算点，其中k为迭代次数.

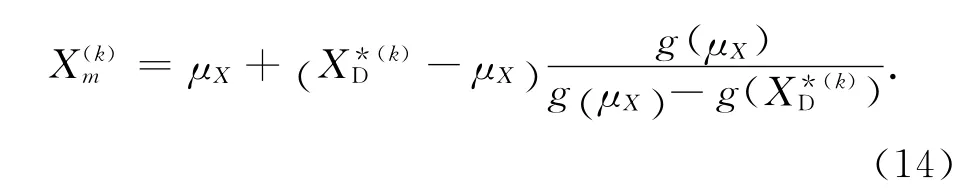
新插值点较接近真实的极限状态曲面，以新插值点为展开点进行下一轮迭代，重复步骤5）～9），直到满足收敛条件为止.

2.2 基于拉丁抽样均匀设计的混合模拟法的实现

利用Matlab语言及软件Ansys可以实现基于拉丁抽样均匀设计的混合模拟法.首先利用Ansys可靠度分析模块（PDS）中Monte-Carlo法的LHS抽样对结构进行200～1 000次抽样，据此计算各随机输入变量的可靠性灵敏度因子.按照灵敏度因子的大小排序，将灵敏度因子≥2.5%的输入变量继续作为随机变量考虑，同时将灵敏度因子＜2.5%的随机输入变量作为确定性变量考虑.在Matlab中根据好格子点法理论，编制使中心化L2-偏差最小的均匀设计表程序［27］，按照生成的均匀设计表选取各随机变量的取样点，并形成对应的均匀设计数据文件.在Ansys可靠度分析模块（PDS）中响应面的用户自定义接口中读入均匀设计数据文件，拟合出均匀设计响应面函数，即为显示化的功能函数.在迭代过程中，借助Matlab编制JC 法程序求解显式化功能函数的可靠度指标及设计验算点.整个方法实现的基本原理及流程如图3所示.当可靠度指标达到计算收敛精度时，上述计算过程退出迭代循环.

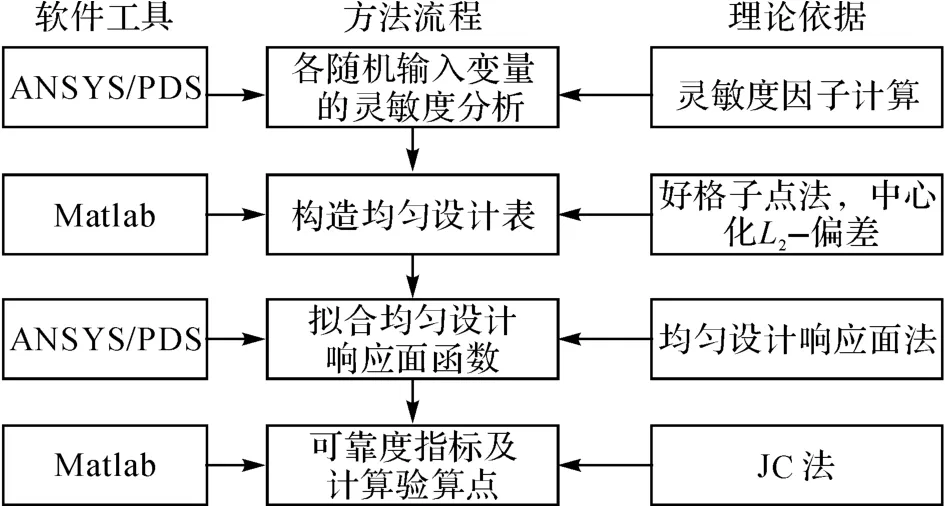
图3 基于拉丁抽样均匀设计的混合模拟法的基本原理及流程图Fig.3 Principle and flow chart of LUH method

3 算例分析

为了验证基于拉丁抽样均匀设计的混合模拟法的适用性，将该方法应用于2个具有较多随机变量、隐式功能函数的经典可靠度分析算例中，并将本文方法的计算结果与传统可靠度计算方法的结果进行对比分析.算例中的结果均列于表2、3、5、6 中.表2、3、5、6中，MC表示Monte-Carlo法，计算结果作为精确解；RSM 表示经典响应面法；IRSM 表示改进响应面法；VPSM 表示利用向量投影取样点的响应面法；FORM 表示一次二阶矩方法；LCH 表示基于拉丁抽样中心复合设计的混合模拟法；LBH 表示基于拉丁抽样Box-Bechnken的混合模拟法；LOH表示基于拉丁抽样正交设计的混合模拟法；LUH 表示基于拉丁抽样均匀设计的混合模拟法，即本文方法.表2、5的相对误差均为结构失效概率的误差.

算例1 如图4所示为三跨十二层建筑的平面框架结构计算简图.各单元的弹性模量均为E＝2.0×107kN／m2，单元截 面 惯 性 矩Ii与 截 面 面 积Ai的关系为Ii＝αi（i＝1，2，…，5） ，其中，αi为截面特性系数，各单元的截面特征如表1所示.随机变量为各单元的截面面积Ai，统计参数如表1 所示.外荷载P 的均值为30kN，变异系数为0.25，属于极值Ⅰ型分布.考虑结构在正常使用的极限状态下，根据规范给出的最大允许水平位移［u］＝H／500＝0.096m（H 为楼高），可以建立极限状态方程：z＝0.096-uk，其中uk为k 点的水平位移.计算结构可靠指标β及失效概率Pf.

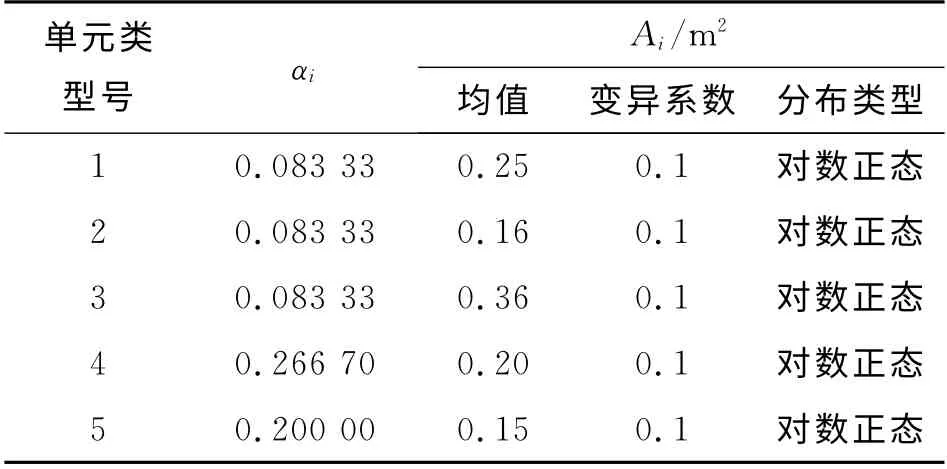
表1 随机变量统计特性Tab.1 Statistic characteristics of random variables

对结构进行200次LHS抽样分析，得出各随机变量的灵敏度因 子，如图5所示.将灵敏度因子＜2.5%的随机变量A2作为确定性变量考虑，其他灵敏度较高的5个输入变量作为随机变量考虑.当运用均匀设计响应面法拟合极限状态方程时，选用偏差为0.191 87的U1＊1（115）均 匀设 计 表 在抽 样空间中选取试验点.各方法对算例1的可靠度分析结果如表2所示.LCH 法、LBH 法、LOH 法以及 本文方法的取样点分布如图6 所示.采用RSM 法、IRSM 法、LOH 法及本文方法计算所得的设计验算点如表3所示.

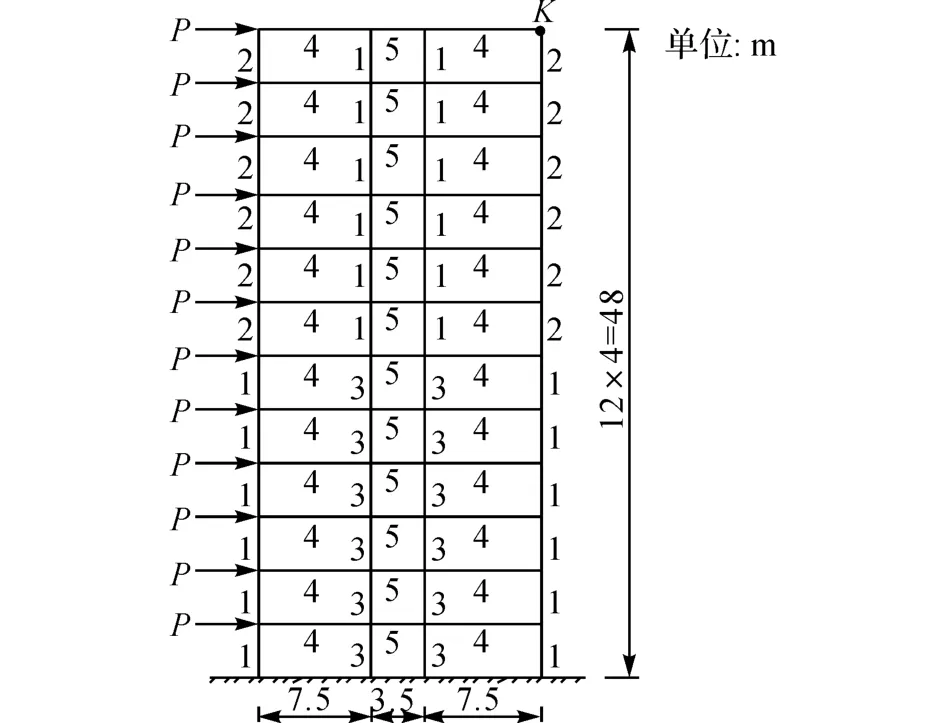
图4 算例1的计算简图Fig.4 Calculation diagram of example 1

图5 算例1的灵敏度因子Fig.5 Sensitivity factors of example 1

基于拉丁抽样正交设计的混合模拟法拟合的功能函数表达式为

表2 算例1的可靠度分析结果Tab.2 Reliability analysis results of example 1

图6 各混合模拟法取样点分布比较Fig.6 Comparison of sample point for each hybrid simulation method

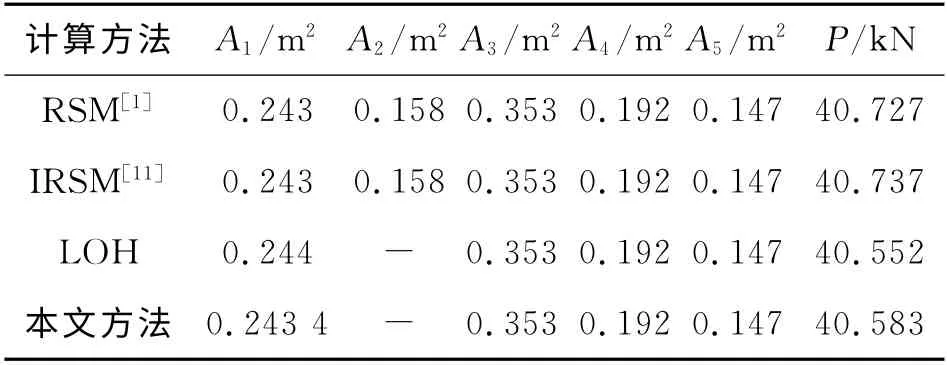
表3 算例1的设计验算点比较Tab.3 Comparison of design points for example 1

基于拉丁抽样均匀设计的混合模拟法拟合的功能函数表达式为

算例2 二十三杆桁架如图7 所示，桁架结构由23个单元组成.其中，E 为弹性模量，A 为横截面面积，输入随机变量的统计参数如表4所示.以桁架中点的位移 D （x） 不超过11.00cm 建立结构的极限状态函数：g（x） ＝0.11-D （x） ，试求解结构的失效概率与可靠指标.

对结构进行200次LHS抽样分析，得出各随机变量的灵敏度因子如图8 所示.将灵敏度因子＜2.5%的随机变量E2、P1、P6作为确定性变量考虑，其他灵敏度较高的7个输入变量作为随机变量考虑.当运用均匀设计响应面法拟合极限状态方程时，选用偏差为0.301 46的（157）均匀设计表在抽样空间中选取试验点.各方法对算例2的可靠度分析结果如表5所示.LCH 法、LBH 法、LOH 法以及本文方法的取样点分布如图9所示.采用LOH法、本文方法计算所得的设计验算点如表6所示.

表4 随机变量统计特性Tab.4 Statistic characteristics of random variables

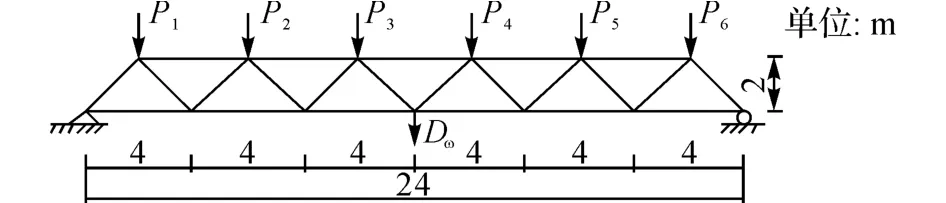
图7 算例2的计算简图Fig.7 Calculation diagram of example 2

图8 算例2的灵敏度因子Fig.8 Sensitivity factors of example 2

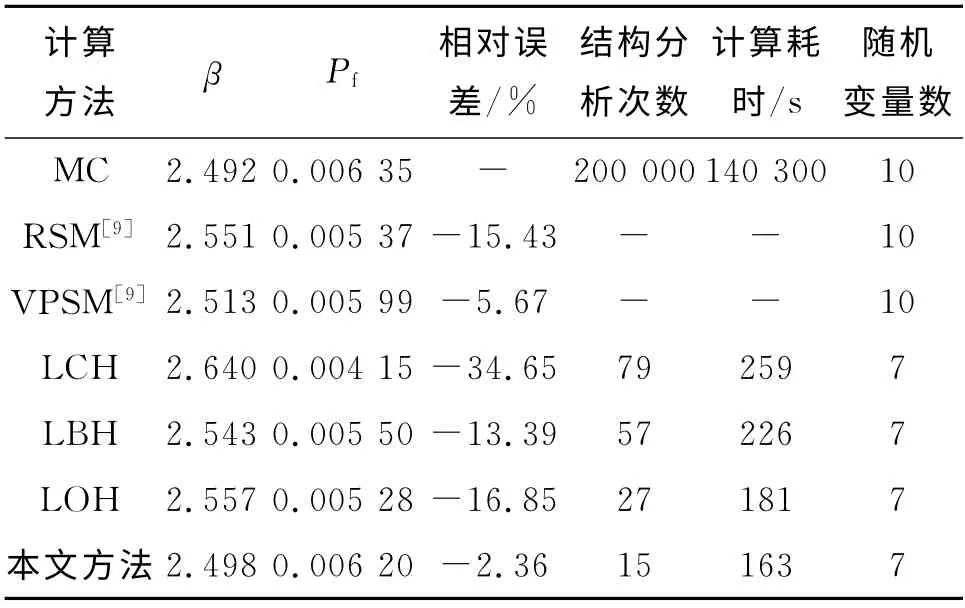
表5 算例2的可靠度分析结果Tab.5 Reliability analysis results of example 2

基于拉丁抽样正交设计的混合模拟法拟合的功能函数表达式为

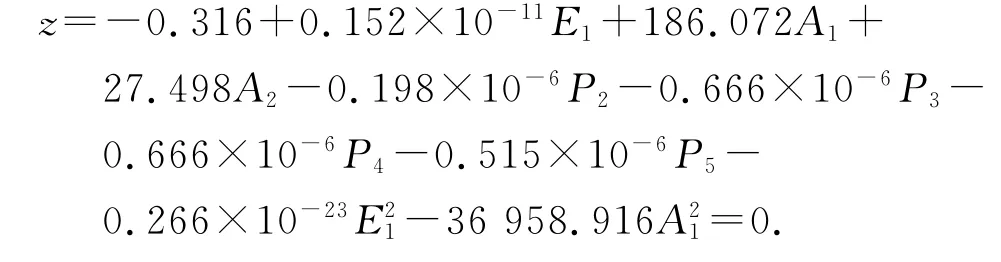
基于拉丁抽样均匀设计的混合模拟法拟合的功能函数表达式为

分析表2、5的可靠度计算结果可知，本文方法的计算结果最接近Monte-Carlo法的精确解，且计算耗时远远小于Monte-Carlo法.同时，本文方法考虑的随机变量数少于常规响应面法，结构分析次数减少，计算效率提高.借助LHS法对随机变量的可靠性灵敏度因子的分析，本文方法剔除了灵敏度较低的随机输入变量对构造响应面函数的干扰，使得计算精度较常规响应面法高.对比4种混合模拟法的计算结果可知，本文方法的精度最高、计算耗时最少.换言之，即在考虑相同的随机变量时，均匀设计响应面法较中心复合设计响应面法、Box-Bechnken响应面法、正交设计响应面法的精度更高、计算效率更好.由此可见，本文方法是可行的，且精度较高.

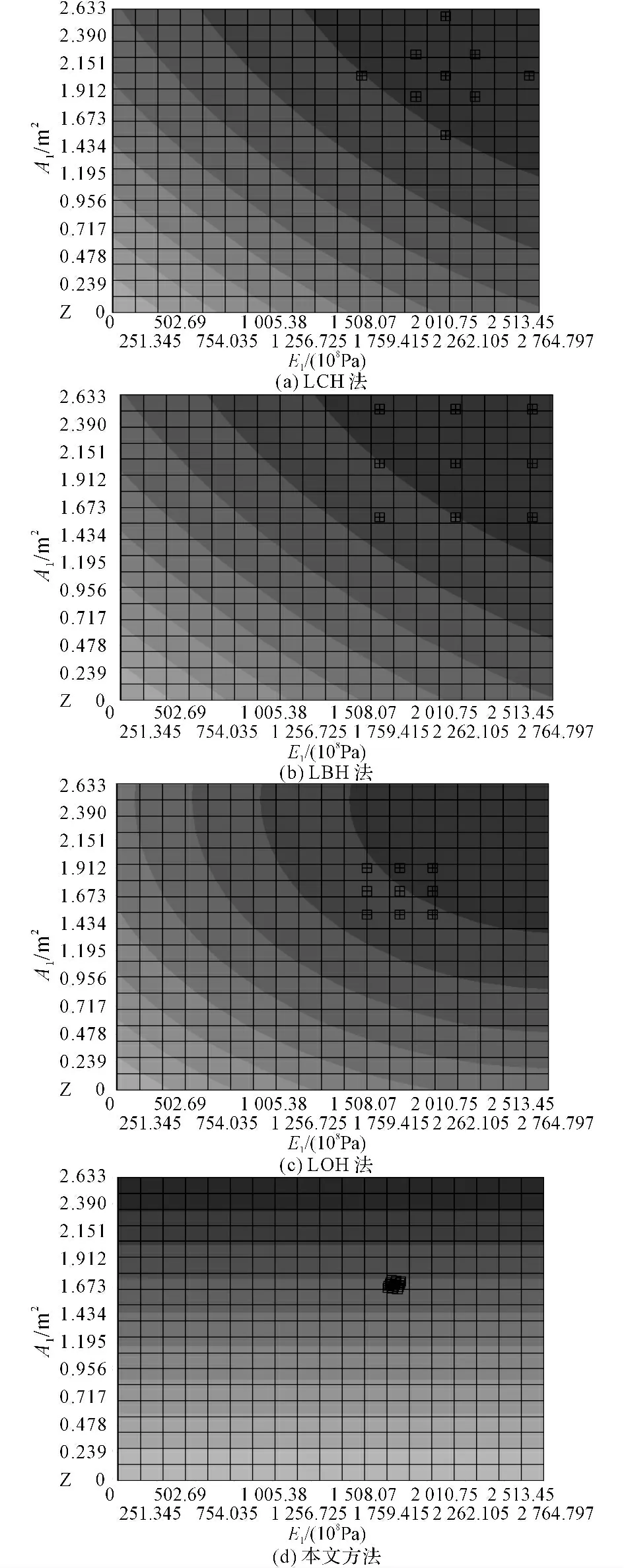
图9 各混合模拟法取样点分布比较Fig 9 Comparison of sample point for each hybrid simulation method

表6 算例2的设计验算点比较Tab.6 Comparison of design points for example 2

对比图6、9中4种混合模拟法的试验取样点分布情况可知，本文方法的试验取样点更接近设计验算点，且在设计验算点周边均匀分散.表3、6的结果显示，采用4种混合模拟法计算出的设计验算点均较接近.

4 工程实例

某已建成的三跨连续刚构桥横跨广西右江主航道，上部构造采用跨径为（85＋160＋85）m 的三向预应力混凝土连续箱梁结构，主梁采用单箱单室的箱形断面.单箱顶宽为13.5m，底宽为7.0m，翼缘板宽为3.25m，支点处梁高9.0m，跨中及梁端梁高2.8m，梁底缘按二次抛物线变化.主墩下部构造采用双壁式墩身，单壁宽为1.6m，两壁中心纵向间距为8.0m.桥梁结构的总体布置图如图10所示.

考虑材料性能参数、几何尺寸参数、荷载效应等的随机性，应用本文提出的LUH 法对三跨连续刚构桥在正常使用极限状态下中跨跨中挠度的可靠性进行分析.

根据文献［28］中统计的材料性能参数、计算模式、几何尺寸参数、作用效应等各种随机变量，本文假定90项随机变量，由于篇幅有限，仅将部分随机变量列于表7.在正常使用极限状态下，根据规范《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2004）可知，连续刚构桥的主梁在车辆荷载作用下的最大竖向挠度不应超过计算跨径的1／600，据此建立极限状态方程：

式中：u为三跨连续刚构桥中跨跨中竖向挠度.根据LUH 法可知，u可以表示为灵敏度因子较高的随机变量的函数.

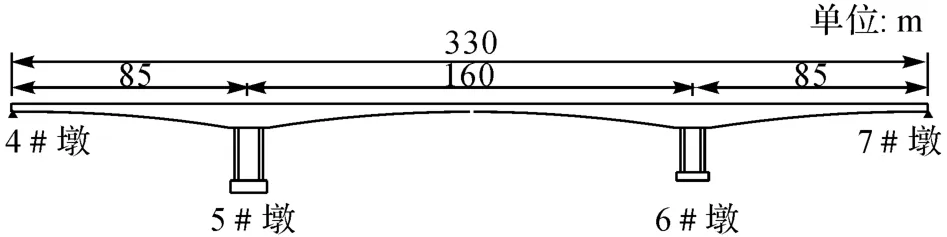
图10 连续刚构桥总体布置图Fig.10 Elevation view of continuous rigid frame bridge

表7 随机变量统计特性Tab.7 Statistic characteristics of random variables

利用ANSYS对连续刚构桥进行确定性结构分析.在ANSYS／Structural中建立三维有限元模型（见图11），共计18 784个单元，29 105个结点.利用ANSYS／PDS对连续刚构桥进行500次LHS抽样分析，得出各随机变量的灵敏度因子如图12所示.将灵敏度因子＜2.5%的随机变量作为确定性变量考虑，其他灵敏度较高的8个输入变量作为随机变量考虑.当运用均匀设计响应面法拟合极限状态方程 时，选用偏差为0.339 1的（178）均匀设计表在抽样空间中选取试验点.采用LOH 法、本文方法计算所得的可靠性指标及设计验算点如表8所示. 基于拉丁抽样均匀设计的混合模拟法拟合的功能函数表达式为

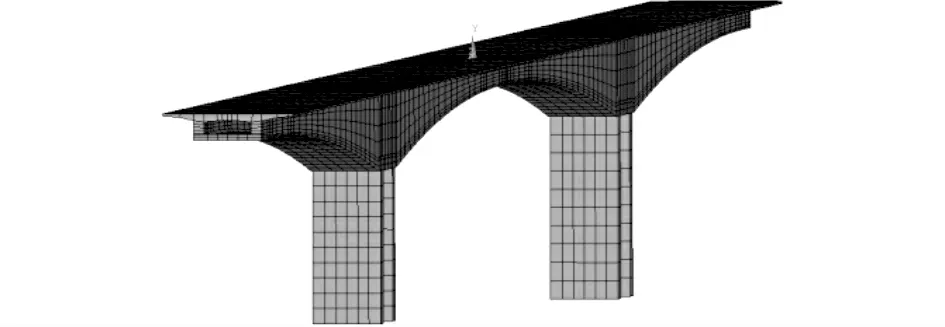
图11 连续刚构桥有限元模型Fig.11 Finite element model of continuous rigid frame bridge

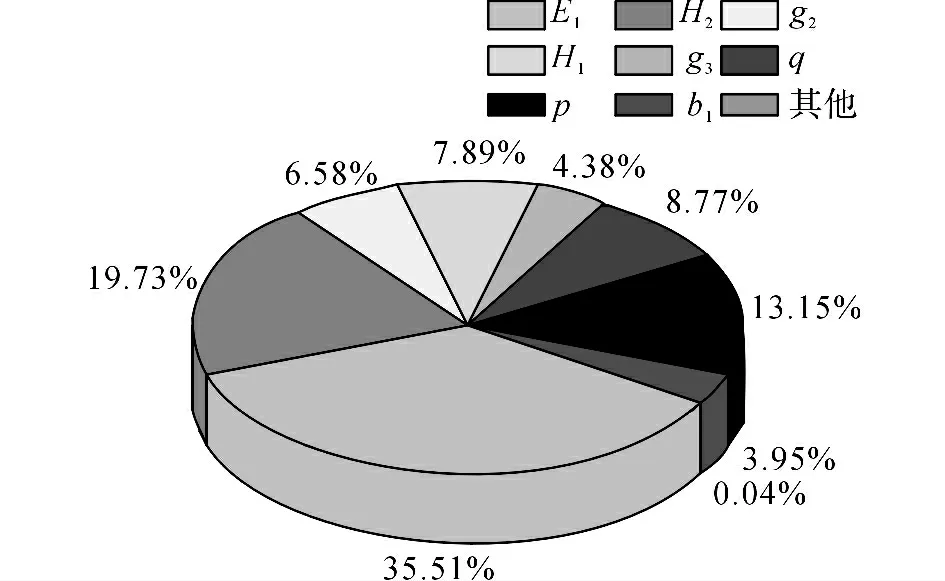
图12 灵敏度因子图Fig.12 Chart of sensitivity factors

由于对该连续刚构桥进行一次确定性结构分析的时间较长，若采用Monte-Carlo法进行可靠度分析，则多次循环所需的计算耗时更冗长，计算效率极低甚至不可行.由于考虑了90项随机变量，若采用响应面法，则所需进行的结构分析次数过多、计算耗时过长且难以拟合出响应面函数.因此，响应面法不可行.采用基于拉丁抽样均匀设计的混合模拟法可以解决该问题，且计算效率较高，如表8所示.

表8 连续刚构桥可靠性计算结果Tab.8 Reliability analysis results of continuous rigid frame bridge

根据文献［14］、［28］中建议正常使用极限状态下的目标可靠度取βT＝1.5.由此可知，该三跨连续刚构桥的中跨跨中挠度满足规范规定的目标可靠指标要求.

5 结 论

（1）本文方法结合了Monte-Carlo法和均匀设计响应面法2种方法的优点，相对Monte-Carlo法节约了大量的计算时间，相对响应面法减少了随机输入变量的数量，从而减少了结构计算次数，提高了计算效率.随着结构随机变量的增多，该方法的计算效率优势将进一步得到体现.本文方法为复杂结构的可靠度分析提供了一条新途径.

（2）本文方法较基于拉丁抽样中心复合设计混合模拟法、基于拉丁抽样Box-Bechnken混合模拟法和基于拉丁抽样正交设计混合模拟法具有更高的计算精度、计算效率.换言之，在考虑相同随机输入变量的条件下，均匀设计响应面法较正交设计响应面法、中心复合设计响应面法、Box-Bechnken设计响应面法具有更高的计算精度和计算效率.

（3）运用LHS法对结构进行抽样分析，可以寻找出对结构可靠性影响较大的因素.在实际工程中，应对这些因素的施工质量进行严格控制，从而使工程结构具有较高的可靠性指标.

（

）：

［1］佟晓利，赵国藩.一种与结构可靠度分析几何法相结合的响 应 面 方 法［J］.土 木 工 程 学 报，1997，30（4）：51-57.TONG Xiao-li，ZHAO Guo-fan.The response surface method in conjunction with geometric method in structural reliability analysis ［J］.China Civil Engineering Journal，1997，30（4）：51-57.

［2］金伟良，袁雪霞.基于LS-SVM 的结构可靠度响应面分析方法［J］.浙江大学学报：工学版，2007，41（1）：44-47.JIN Wei-liang，YUAN Xue-xia.Response surface method based on LS-SVM for structural reliability analysis［J］.Journal of Zhejiang University：Engineering Science，2007，41（1）：44-47.

［3］OLSSON A M J，SANDBERG G E.Latin hypercube sampling for stochastic finite element analysis［J］.Journal of Engineering Mechanics，2002，128（1）：121-125.

［4］熊学玉，顾炜.基于改进LHS方法的预应力混凝土结构长期 性 能 概 率 分 析［J］.工 程 力 学，2010，27（4）：163-168.XIONG Xue-yu，GU Wei.Long-term performance probabilistic analysis of PCstructure based on improved LHS method［J］.Engineering Mechanics，2010，27（4）：163-168.

［5］JIN Wei-liang.Reliability-based design for Jacket platform under extreme loads［J］.China Ocean Engineering，1996，10（2）：145-160.

［6］金伟良.结构可靠度数值模拟的新方法［J］.建筑结构学报，1996，17（3）：63-72.JIN Wei-liang.A new approach to numerical simulation of structural reliability analysis［J］.Journal of Building Structures，1996，17（3）：63-72.

［7］JIN Wei-liang.Importance sampling method in V-space［J］.China Ocean Engineering，1997，11（2）：127-150.

［8］唐纯喜，金伟良，陈进.结构失效面上的复合蒙特卡罗方法［J］.浙江大学学报：工学版，2007，41（6）：1012-1016.TANG Chun-xi，JIN Wei-liang，CHEN Jin.Composite Monte Carlo method on structural failure hyperplane［J］.Journal of Zhejiang University：Engineering Science，2007，41（6）：1012-1016.

［9］CHEN Jian-yun，QIANG Xu，FAN Shu-li，et al.Improved response surface method for anti-slide reliability analysis of gravity dam based on weighted regression［J］.Journal of Zhejiang University：Science A，2010，11（6）：432-439.

［10］SOARES R C，MOHAMEDB A，VENTURINI W S.Reliability analysis of non-linear reinforced concrete frames using the response surface method［J］.Reliability Engineering and System Safety，2002，75（1）：1-6.

［11］WONG S M，HOBBS R E，ONOF C.An adaptive response surface method for reliability analysis of structures with multiple loading sequences［J］.Reliability Engineering and System Safety，2002，75（1）：1-6.

［12］KIM S H，NA S W.Response surface method using vector projected sampling points［J］.Structural Safety，1997，19（1）：3-19.

［13］王宇，王春磊，汪灿，等.边坡可靠性评价的向量投影响应面研究及应用［J］.岩土工程学报，2011，33（9）：1434-1440.WANG Yu，WANG Chun-lei，WANG Can，et al.Reliability evaluation of slopes based on vector projection response surface and its application［J］.Chinese Journal of Geotechnical Engineering，2011，33（9）：1434-1440.

［14］张哲，李生勇，石磊，等.结构可靠度分析中的改进响应面法及其应用［J］.工程力学，2007，24（8）：111-115.ZHANG Zhe，LI Sheng-yong，SHI Lei，et al.An improved response surface method for structural reliability analysis and its application ［J］. Engineering Mechanics，2007，24（8）：111-115.

［15］李洪双，吕震宙，赵洁.基于加权线性响应面法的支持向量机可靠性分析方法［J］.工程力学，2007，24（5）：67-71.LI Hong-shuang，LV Zhen-zhou，ZHAO Jie.A support vector method for reliability analysis based on weighted linear response surface ［J］.Engineering Mechanics，2007，24（5）：67-71.

［16］吕大刚，贾明明，李刚.结构可靠度分析中的均匀设计响应面法［J］.工程力学，2011，28（7）：109-115.LV Da-gang，JIA Ming-ming，LI gang.Uniform design response surface method for structural reliability analysis［J］.Engineering Mechanics，2011，28（7）：109-115.

［17］吕大刚，贾明明，李刚.基于均匀设计响应面法的钢框架结构抗震可靠度分析［J］.哈尔滨工业大学学报，2011，43（4）：1-5.LV Da-gang，JIA Ming-ming，LI gang.Seismic reliability analysis of steel frame structures based on uniform design response surface method［J］.Journal of Harbin Institute of Technology，2011，43（4）：1-5.

［18］金伟良，唐纯喜，陈进.基于SVM 的结构可靠度分析响应面方法［J］.计算力学学报，2007，24（6）：713-718.JIN Wei-liang，TANG Chun-xi，CHEN Jin.SVM based on response surface method for structural reliability analysis［J］.Chinese Journal of Computational Mechanics，2007，24（6）：713-718.

［19］LIU Ji，LI Yun.An improved adaptive response surface method for structural reliability analysis［J］.Journal of Central South University，2012，19（4）：1148-1154.

［20］赵威，王伟.偏最小二乘回归在响应面法可靠度分析中的应用［J］.工程力学，2013，30（2）：272-277.ZHAO Wei，WANG Wei.Application of partial least squares regression in response surface for analysis of structural reliability［J］.Engineering Mechanics，2013，30（2）：272-277.

［21］DENG Jian，GU De-sheng，LI Xi-bing，et al.Structural reliability analysis for implicit performance functions using artificial neural network ［J］.Structural Safety，2005，27（1）：25-48.

［22］CHENG Jin，LI Q S，XIAO Ru-cheng.A new artificial neural network-based response surface method for structural reliability analysis［J］.Probabilistic Engineering Mechanics，2008，23（1）：51-63.

［23］CHENG Jin，LI Q S.Artificial neural network-based response surface methods for reliability analysis of prestressed concrete bridges［J］.Structure and Infrastructure Engineering，2012，8（2）：171-184.

［24］方开泰，马长兴.正交与均匀试验设计［M］.北京：科学出版社，2001.

［25］张伟.结构可靠性理论与应用［M］.北京：科学出版社，2009.

［26］郭彤，李爱群，缪长青，等.数值模拟联合算法及其在润扬大桥可靠度评估中的应用［J］.土木工程学报，2006，39（9）：80-85.GUO Tong，LI Ai-qun，MIAO Chang-qing，et al.Combined numerical simulation method and its application on the reliability assessment of Runyang bridge［J］.China Civil Engineering Journal，2006，39（9）：80-85.

［27］曹慧荣，李莉.均匀设计表的MATLAB实现［J］.统计与决策，2008，21（6）：144-146.CAO Hui-rong，LI Li.Uniform design table in Matlab［J］.Statistics and Decision，2008，21（6）：144-146.

［28］李扬海，鲍卫刚，郭修武，等.公路桥梁结构可靠度与概率极限状态设计［M］.北京：人民交通出版社，1997.