基于随机参数Gamma过程的剩余寿命预测方法
王浩伟,徐廷学,刘 勇
(1.海军航空工程学院 兵器科学与技术系,山东 烟台264000;2.海军航空工程学院 接改装训练大队,山东 烟台264000)
近些年,越来越多的高可靠性产品出现在军工、航空、航天等领域,这类产品在投入使用之前通常利用加速试验预测其可靠性水平及进行定寿.对于某些具有老化特征的高可靠性产品,加速老化试验是一种效率较高的试验手段[1-3],因为这类产品的某些性能指标会随时间老化,对性能老化量进行测量、建模,则可推测出产品的寿命信息.例如某型导弹电连接器的接触电阻在使用过程中逐渐增大,当接触电阻老化量达到失效阈值时发生失效.
在产品投入使用之后,准确预测产品的剩余寿命是实现产品视情维修、提高装备战备完好率的关键.由于产品个体之间不可避免存在差异,加速老化试验得到的产品总体信息不能反映出个体差异,无法推测个体的真实剩余寿命.高可靠性产品在额定应力下的老化速率很低,现场测量到的性能老化数据难以对其老化趋势正确建模,也不能准确地预测个体的剩余寿命.研究如何融合加速老化数据和现场测量数据进行准确的个体剩余寿命预测,对有效地开展视情维修、精确化保障等具有较强的工程指导意义.
产品的老化过程具有不确定性,适合采用随机过程进行建模,Gamma过程被广泛用于对具有单调变化趋势的老化过程进行建模[4-5].为了描述个体差别,可以使用具有随机参数的Gamma过程;为了便于Bayesian统计推断,大多采用参数的共轭先验分布假定[6-7]:形状参数为一常量,尺度参数为一服从Gamma分布的随机变量.这种假定具有很好的统计特性,但难免会出现形状参数与假定的Gamma分布拟合不理想的情况.本文研究使用参数的非共轭先验分布,其中尺度参数和形状参数都设为随机变量,通过拟合优度检验确定它们的最优分布类型.
综上所述,本文针对老化规律符合Gamma过程的产品,将加速老化数据作为先验信息,将产品个体在额定应力下的测量数据作为现场信息,使用参数的非共轭先验分布进行Bayesian统计推断,进而预测个体剩余寿命.
1 基于Gamma过程的剩余寿命模型
设Y(t)表示产品在时刻t的性能老化量并且有Y(0)=0,如果Y(t)为Gamma过程,则其独立、非负增量ΔY(t)=Y(t+Δt)-Y(t)服从如下Gamma分布:

式中:Ga(·)表示Gamma分布函数,α(α>0)为形状参数,β(β>0)为尺度参数,Λ(t)为时间t的函数并且有Λ(0)=0.根据Gamma分布的可加性可知,Y(t)~Ga(α·Λ(t),β),概率密度函数(PDF)为

当Y(t)首次达到失效阈值D 时定义为样品失效,可靠度函数可由下式得出:

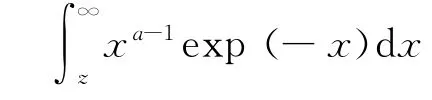

由于式(4)难以进行统计计算,一般采用BS分布对F(t;D)近似拟合[8].进行如下时间尺度转换z =Λ(t),CDF可以被近似表示为

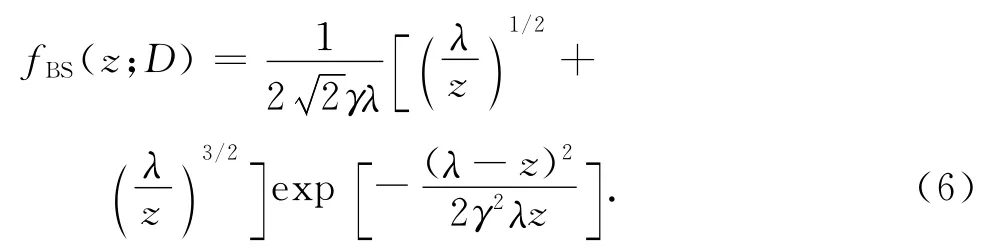

2 确定随机参数的先验分布
由于存在个体差异,每个产品的老化过程并不一致,老化模型的参数值也不同,但对于出自同一总体的个体,可以认为参数值服从同一分布函数.设形状参数αi和尺度参数βi 分别服从αi~fα(a,b),βi~fβ(c,d),且fα(a,b)与fβ(c,d)之间不相关,π(α,β)为α和β 的联合概率密度函数,则有π(α,β)=fα(a,b)·fβ(c,d).
2.1 加速应力下的参数值估计
设S0为正常工作应力,Sk为第k 个加速应力,yijk为第j 个产品在Sk下的第i 次测量值,tijk为对应的测量时刻,其中i=1,2,…,n1;j=1,2,…,n2;k=1,2,…,n3.Δyijk=yijk-y(i-1)jk为 老 化 量 的 增量,ΔΛ(tijk)=Λ(tijk)-Λ(t(i-1)jk)为时间增量.根据每个样品的n1次测量数据建立似然函数为
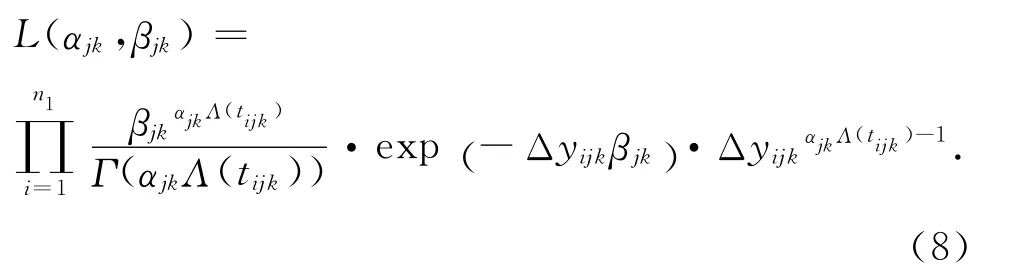
将测量数据(Δyijk,ΔΛ(tijk))代入式(8),可以估计每个样品参数值(αjk,βjk),形式如下:
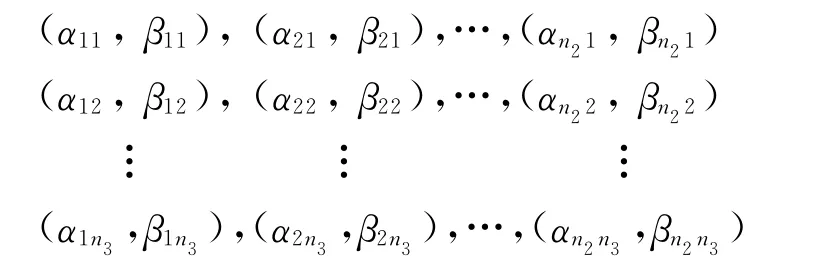
2.2 加速因子估计及参数值折算
加速因子的一种等效定义可以由Nelson假设推出,设Fi(ti)、Fj(tj)分别为产品在应力Si和Sj下的累积失效概率,如有Fi(ti)=Fj(tj),则可将Si相当于Sj的加速因子定义为

周源泉等[9-11]指出,AFij为一个与可靠度无关的常数,是保证产品在加速试验中失效机理不变的充分必要条件.对于任意ti恒有下式成立:

将式(3)代入式(10),并设Λ(t)=t,可得
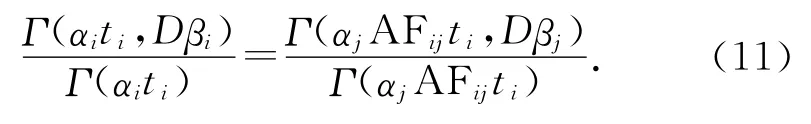
若要保证式(11)恒成立,须满足:

从而可得
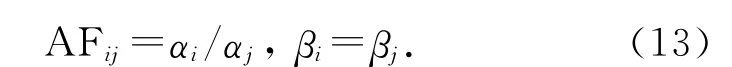
可知,β在各应力下不变,而α随着应力S 的变化而改变.α与S 的关系可以用加速模型来描述,假设应力为温度T,加速模型为Arrhenius模型,α 可以表示为

将式(14)代入式(13),可得

将加速应力下的αjk代入式(14),通过最小二乘估计可得,进一步可由式(15)计算出Tk相对于T0的加速因子AFk0.由αh0=αjk/Kk0可得αjk在T0下的折算值αh0,由βh0=βjk 可得βjk 在T0下的折算值βh0,h=1,2,…,m,m 为试验产品总数.
2.3 确定参数的分布类型
使用Anderson-Darling 拟合优度检验的方法确定αh0、βh0的最优拟合分布类型.因为Exponential分布、Normal分布、LogNormal分布、Weibull分布、Gamma分布包含了绝大多数参数分布情况,故在这5种分布中选择最优拟合的分布类型.
Anderson-Darling统计量的AD 值越小,说明备选分布类型与数据拟合得越好[12],计算式如下:
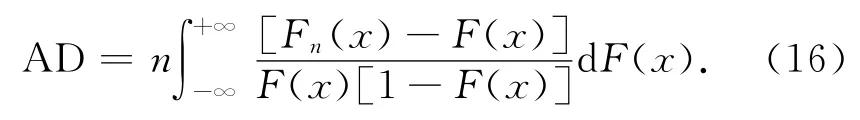
式中:Fn(x)为经验分布函数,F(x)为累积分布函数.此外,可以利用Anderson-Darling 对参数的分布类型假设进行检验,若Anderson-Darling的p 值大于显著性水平0.05,则可以接受原假设.
2.4 估计随机参数的超参数值
假设参数的先验分布确定为αh0~Ga(a,b),βh0~LN(c,d),其中超参数a、b 为Gamma分布的形状参数和尺度参数,超参数c、d 为LogNorm 分布的对数均值和对数标准差.根据各自分布的PDF建立极大似然方程.对于Gamma 分布,似然函数[13]为

对于LogNorm 分布,似然函数为

3 Bayesian统计推断
某个运行中的产品与老化试验中的样品出自同一总体,参数值服从同一分布,可以使用Bayesian方法估计参数的后验均值.
设经过定期检测得到某一个体的i个性能老化数据为Y=[Y(t1),Y(t2),…,Y(ti)],π(α*,β*|Y)为联合后验PDF,L(Y|αh0,βh0)为极大似然函数,则有

可得α*、β*的边缘密度函数为
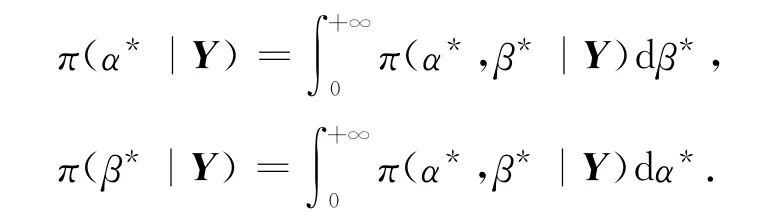
进一步通过计算α*、β*的期望得到随机参数的后验均值:

4 实例应用
4.1 加速老化试验
某型导弹电连接器的主要失效原因是接触电阻老化,老化速率主要受温度和湿度的影响,温湿度可以影响插针表面氧化物的生成,氧化物的堆积导致接触电阻不断增大,最终引起接触失效[15].试验中采用恒定应力加速老化试验方式,将温度、湿度作为综合加速应力.
1)试验样本量为24,平均分配在3组应力下:S1(t1=90 ℃,RH1=75%),S2(t2=90 ℃,RH2=95%),S3(t3=130 ℃,RH3=95%).
2)S1下对样品共进行15次测量,测量间隔为96h;S2下进行12次测量,测量间隔为72h;S3下进行10次测量,测量间隔为48h.
3)在正常工作应力S0(t0=55℃,RH0=60%)下对样品的性能老化量进行测量,该型电连接器接触电阻的失效阈值为5mΩ.
4.2 确定随机参数的先验分布
测量到的样品老化情况如图1~3所示,对各样品是否服从Gamma老化过程进行检验.根据文献[8]可 知,Δyiβ/(Δtiα)近 似 服 从 均 值 为1-1/(9Δtiα)、方 差 为1/(9Δtiα)的 正 态 分 布.将Δyiβ/(Δtiα)正态标准化后,可以通过判断是否服从标准正态分布得出老化过程是否为Gamma过程的结论.通过Anderson-Darling统计量进行置信度为95%的标准正态分布假设检验,证明所有样品的老化过程都服从Gamma过程.
加速应力下所有样品参数的极大似然估计值(MLE)如表1所示.

表1 加速应力下参数(μ,σ2)的极大似然估计值Tab.1 MLEs of(μ,σ2)of each sample at accelerated stresses
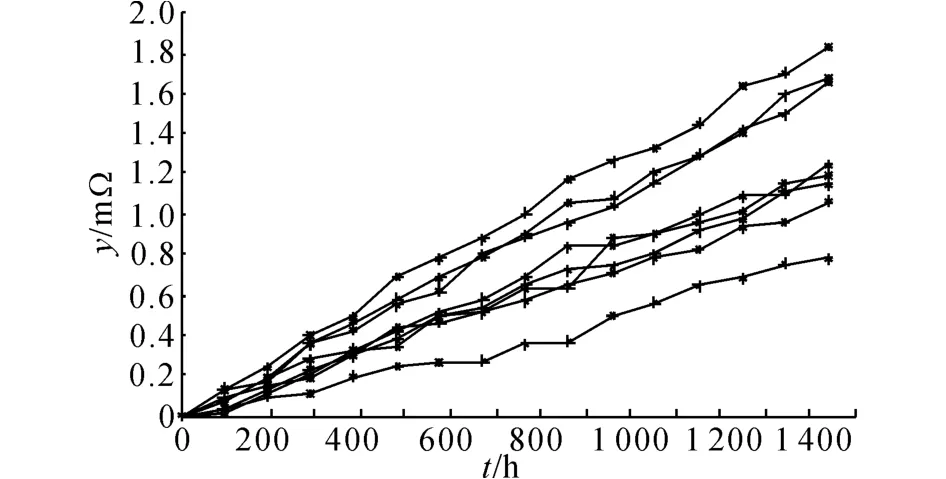
图1 S1 下样品老化曲线Fig.1 Aging curves of samples at S1
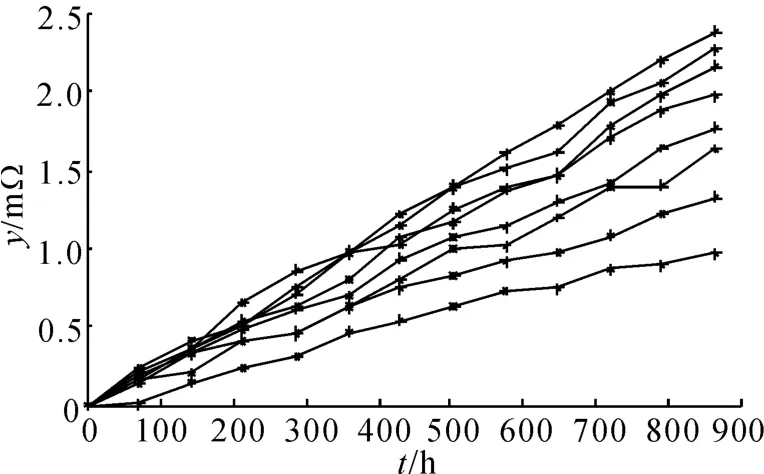
图2 S2 下样品老化曲线Fig.2 Aging curves of samples at S2

图3 S3 下样品老化曲线Fig.3 Aging curves of samples at S3
对于温度、湿度综合应力,可以用广义艾林模型描述α与两应力之间的关系:
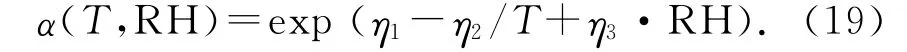
产品的加速因子表达式如下:
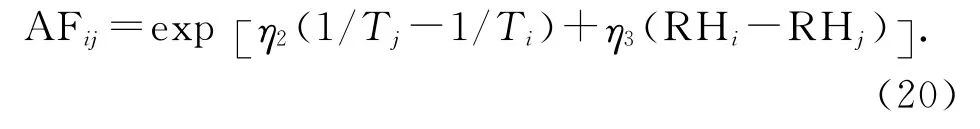
利用AFi0对表1中的各参数估计值进行折算,结果如表3所示.
通过Anderson-Darling 统计量分别对αh0、βh0备选分布类型进行拟合优度检验,结果如表4所示.

表2 AFi0值Tab.2 Values of AFi0
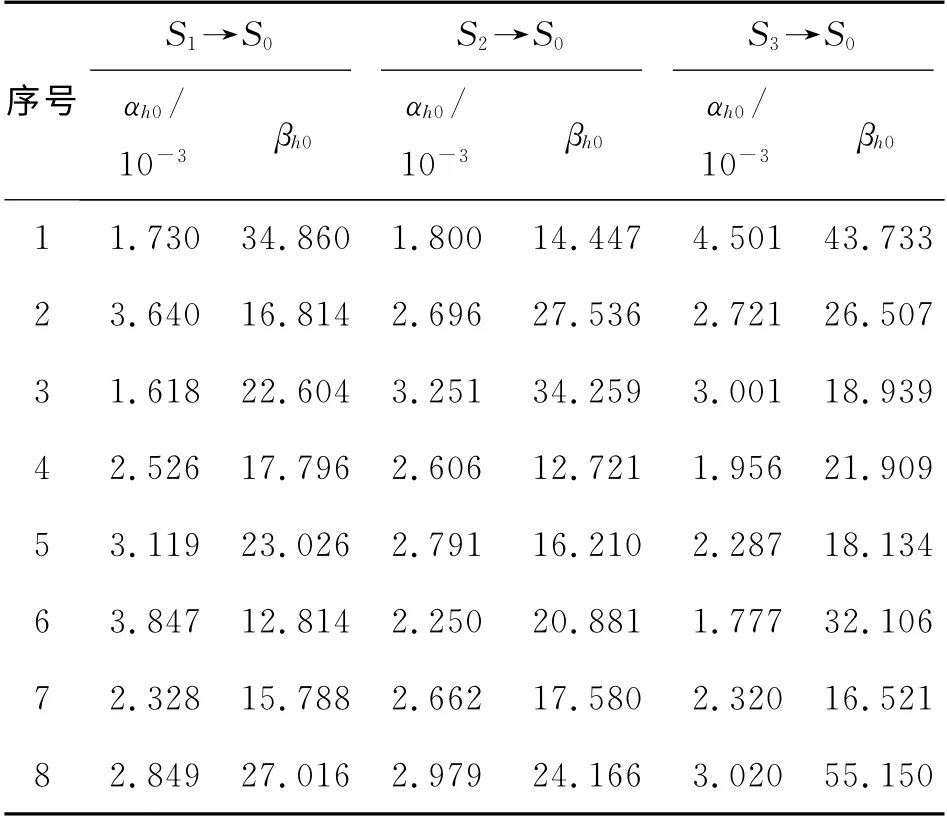
表3 参数的折算值(αh0,βh0)Tab.3 Transformed(αh0,βh0)

表4 αh0、βh0在各分布下的AD值Tab.4 ADs ofαh0,βh0at different distribution types
由表4可知,αh0最优服从Gamma分布,βh0最优服从LogNorm分布.若使用参数的共轭先验分布,则须指定βh0服从Gamma分布.在本实例中,βh0与Gamma分布的拟合效果一般,使用共轭先验分布进行Bayesian统计推断不合适,所以采用参数的非共轭先验分布.根据式(17)、(18)可得超参数的极大似然估计值,参数的先验分布确定为αh0~Ga(15.766,5.887×103),βh0~LN(3.097,0.378).
4.3 预测剩余寿命
额定应力S0下运行的某电连接器每隔3个月检测一次,共获取10组接触电阻测量值:0.233、0.494、0.731、1.037、1.348、1.512、1.830、2.203、2.529、2.811mΩ.依次使用前i个测量数据(6≤i≤10),预测产品剩余寿命.若仅利用现场测量数据,则参数估计值及剩余寿命预测值如表5所示.若使用Bayesian统计推断的方法,则可得参数的后验均值和剩余寿命预测值,如表6所示,其中通过Bootstrap方法给出95%置信区间.
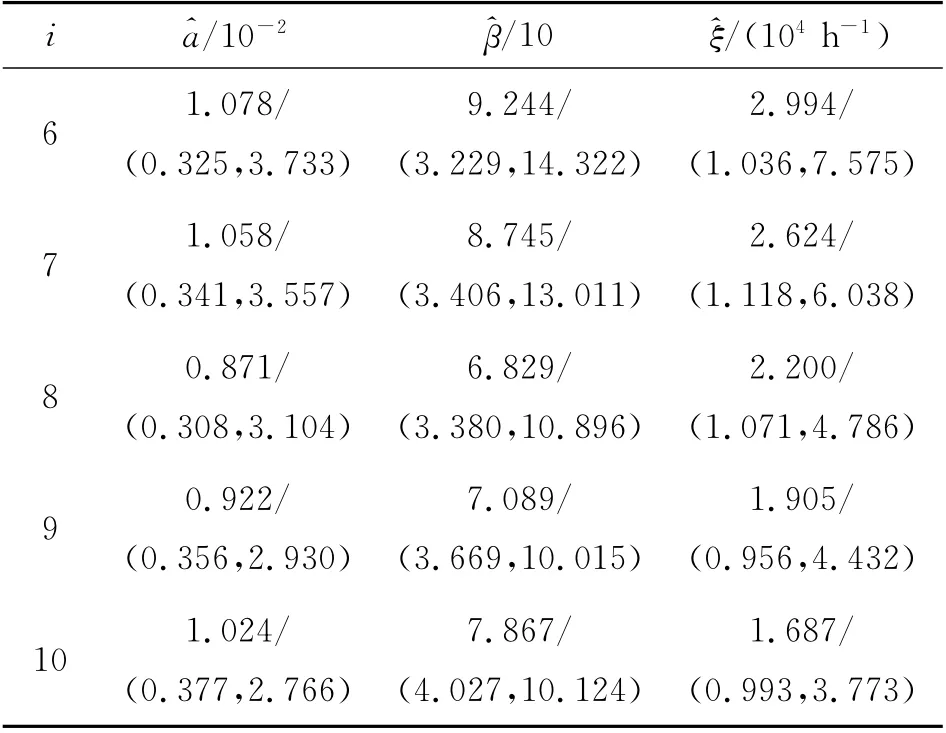
表5 仅利用现场测量数据所得估计值Tab.5 Estimates only from field measuring data
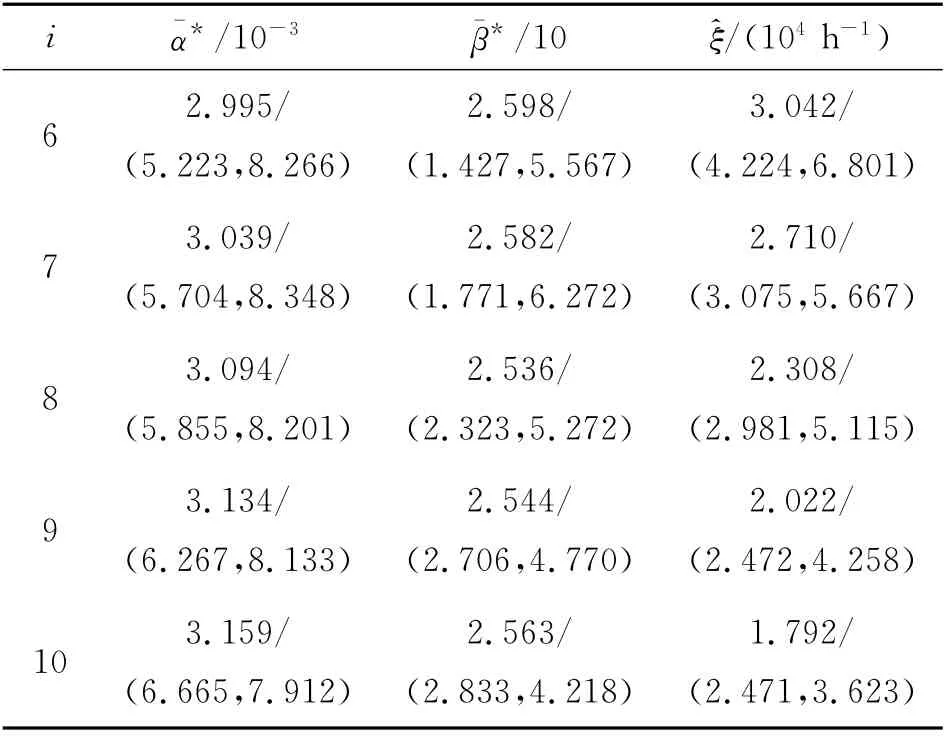
表6 使用Bayesian统计推断方法所得估计值Tab.6 Estimates from Bayesian method
由表5、6可知,仅利用现场数据时,估计值与预测值的置信区间较大,说明估计精度不高.利用Bayesian统计推断时,相同估计值的置信区间比仅利用现场数据时小,说明估计精度得到了提高.产品在第i次(6≤i≤10)检测时,利用Bayesian方法得到剩余寿命的PDF和CDF,如图4所示.可知,随着现场数据的增多,PDF曲线和CDF曲线逐渐变窄,说明剩余寿命的预测精度越来越高.图5给出3种方法的剩余寿命预测曲线:1)仅利用现场数据;2)仅利用先验数据;3)Bayesian统计推断.利用方法1)和2)得出的预测曲线之间有较明显的差异,说明个体和总体的寿命特征不一致,不能相互替代.利用方法3)得出的预测曲线在方法1)和方法2)之间,是因为对现场数据和先验数据进行了融合,该预测结果的可信度较高.由各预测曲线的间距可知,与先验数据相比,现场数据对融合预测结果的影响更大.

图4 剩余寿命概率密度函数变化情况Fig.4 Plot of probability density function of residual life
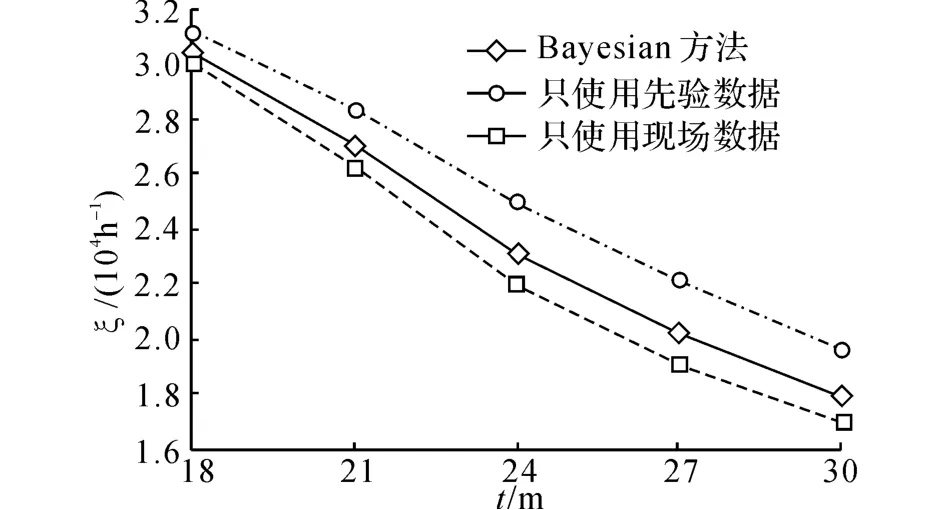
图5 利用3种方法得到的剩余寿命预测值Fig.5 Residual life obtained from three different methods
5 结 论
(1)加速老化试验已成为评估产品寿命的重要途径,基于Bayesian的剩余寿命预测方法融合了加速老化数据,提高了预测结果的可信度,可以实现预测值的实时更新,为产品的视情维修提供了重要参考.
(2)共轭先验分布假定只将Gamma过程的尺度参数看作随机变量,并且要求随机参数服从Gamma分布,这可能会出现拟合不理想的情况.共轭先验分布不预先假定随机参数的分布类型,具有良好的工程应用性.
(3)加速因子是分析、处理加速试验数据的桥梁和纽带,可以将加速应力下的试验信息折算到工作应力下处理,为解决复杂可靠性建模与评估问题提供了有益的思路.
(
):
[1]NELSON W B.Analysis of performance:degradation data from accelerated tests[J].IEEE Transactions on Reliability,1981,30(2):149-155.
[2]林瑞进,陈文华,刘娟,等.航天电连接器加速性能退化试验可行性研究[J].工程设计学报,2010,17(4):318-320.LIN Rui-jin,CHEN Wen-hua,LIU Juan,et al.Research on feasibility of accelerated degradation test for aerospace electrical connector[J].Journal of Engineering Design,2010,17(4):318-320.
[3]葛蒸蒸,李晓阳,姜同敏.费用约束下含应力优化的CSADT 设 计[J].北 京 航 空 航 天 大 学 学 报,2011,37(10):1277-1278.GE Zheng-zheng,LI Xiao-yang,JIANG Tong-min.Planning of CSADT with stress optimization under cost constraint[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(10):1277-1278.
[4]WANG X.Nonparametric estimation of the shape function in a Gamma process for degradation data[J].The Canadian Journal of Statistics,2009,37(1):102-118.
[5]TSAI C C,TSENG S T,BALAKRISHNAN N.Optimal design for degradation tests based on Gamma processes with random effects[J].IEEE Transactions on Reliability,2012,61(2):604-613.
[6]WANG X L,JIANG P,GUO B,et al.Real-time reliability evaluation for an individual product based on change-point Gamma and Wiener process[J].Quality and Reliability Engineering International,2014,30(4):513-525.
[7]VAN NOORTWIJK J M.A survey of the application of Gamma processes in maintenance[J].Reliability Engineering and System Safety,2009,94(1):2-21.
[8]WANG H W,XU T X,MI Q L.Lifetime prediction based on Gamma processes from accelerated degradation data[J].Chinese Journal of Aeronautics,2015,28(1):172-179.
[9]周源泉,翁朝曦,叶喜涛.论加速系数与失效机理不变的条件(Ⅰ):寿命型随机变量的情况[J].系统工程与电子技术,1996,18(1):55-66.ZHOU Yuan-quan,WENG Chao-xi,YE Xi-tao.Study on accelerated factor and condition for constant failure mechanism [J].Systems Engineering and Electronics,1996,18(1):55-66.
[10]杨宇航,周源泉.加速寿命试验的理论基础(Ⅰ)[J].推进技术,2001,22(4):276-278.YANG Yu-hang, ZHOU Yuan-quan. Theoretical foundation of accelerated life testing(Ⅰ)[J].Journal of Propulsion Technology,2001,22(4):276-278.
[11]王浩伟,徐廷学,赵建忠.融合加速退化和现场实测退化数据的剩余寿命预测方法[J].航空学报,2014,35(12):3350-3357.WANG Hao-wei,XU Ting-xue,ZHAO Jian-zhong.Residual life prediction method fusing accelerated degradation and field degradation data[J].Acta Aeronautica et Astronautica Sinica,2014,35(12):3350-3357.
[12]GRACE A W,WOOD I A.Approximating the tail of the Anderson-Darling distribution[J].Computational Statistics and Data Analysis,2012,56(12):4301-4311.
[13]TSENG S T,BALAKRISHNAN N,TSAI C C.Optimal step-stress accelerated degradation test plan for Gamma degradation processes[J].IEEE Transactions on Reliability,2009,58(4):611-618.
[14]NTZOUFRAS I.Bayesian modeling using WinBUGS[M].New York:Wiley,2009:12-55.
[15]王浩伟,徐廷学,周伟.综合退化数据与寿命数据的某型电连接器寿命预测方法[J].上海交通大学学报,2014,48(5):702-706.WANG Hao-wei,XU Ting-xue,ZHOU Wei.Lifetime prediction method for missile electrical connector synthesizing degradation data and lifetime data[J].Journal of Shanghai Jiao Tong University,2014,48(5):702-706.

