基于卡尔曼滤波的巡视机器人能耗估计

付兴伟，吴功平，周 鹏，于 娜

（武汉大学 动力与机械学院，湖北 武汉430072）

面对复杂艰险的输电线路环境，采用人工巡视线路的局限性越来越明显，巡视机器人［1］的出现为架空线路的日常检测提供了新的思路.巡视机器人在巡检过程中一般采用可充电电池进行供电，本文研究的机器人采用锂电池供电.

为了避免巡视机器人在巡检过程中因电量不足停在杆塔中央以及无法到达预定杆塔（方便机器人上下线的杆塔），除了需要了解锂电池当前的荷电状态（SOC），还要估计到达预定的杆塔需要消耗多少电量.其中锂电池的SOC［2-4］估计目前已经进行了大量的研究，相对来说比较成熟；在已知线路的工况参数（档段的档距、高差、线路型号等）下，对机器人到达预定的杆塔所需的能耗进行准确的估计，目前的研究较少，还没有发现相关的文献资料.因此，该问题成为巡视机器人在走向实用化过程中需要解决的一个关键性技术问题.

基于上述问题，本文通过理论分析建立基于高压输电线路档段工况参数的能耗模型.通过自适应卡尔曼滤波对能耗的预测值作了进一步修正，提高了估计精度，为机器人的安全巡检提供了理论支撑，具有重要的工程应用价值.

1 线路环境及机器人机构构型

如图1所示为巡视机器人进行巡检时输电线路的线路环境，由连续的档段组成，每个档段包括相邻的杆塔、杆塔之间的线路以及悬垂线夹、防震锤等金具.

为了提升机器人的巡检效率，简化机器人的运动规划，避免复杂的姿态调整进行越障行驶，研制了巡视机器人，实物图如图2（a）所示.机构构型简图如图2（b）所示，由行走关节（行走轮）、压紧关节（压紧轮）和移动关节组成，共有3个自由度.行走关节（行走轮）具有移动副1，使巡视机器人具有行走功能；压紧关节（压紧轮）具有移动副2，可以使压紧轮沿着手臂上下移动；移动关节具有左右移动的移动副3，可以使手臂具有在机体上移动的功能.

行驶过程中只包含2个动作：滚行和爬行.滚行即压紧关节（压紧轮）松开，行走关节（行走轮）直接行使；爬行即通过后臂的压紧关节（压紧轮）压紧线路，通过移动关节使得前臂和机体向前挪动，然后前臂压紧线路，后臂松开线路，通过移动关节使得后臂向前挪动，如此交替，完成越障.

图1 线路环境Fig.1 Environment of transmission line

图2 巡视机器人的实物和机构构型简图Fig.2 Diagram of robot’s prototype and mechanism

2 能耗建模

通过对基于线路环境参数的输电线路的数学建模以及对机器人匀速行驶时的力学建模，得到巡视机器人的能耗模型.

2.1 输电线路建模

如图3 所示，输电线路（图中用曲线段AC 表示）呈斜抛物线状.在工程应用中，输电线路建模经常用斜抛物线公式［5］.

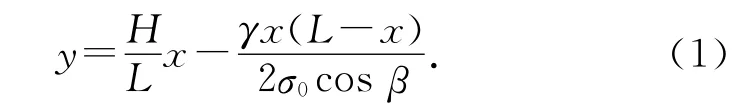
式中：L 为两相邻杆塔的水平距离，即图中输电线路的悬挂点A 点到C 点的距离；H 为指输电线路的悬挂点A 点与C 点之间的高差；σ0为输电线路最低点B 点的应力，即水平应力；γ为输电线路的比载；β为输电线路在相邻杆塔悬挂点即A 点和C 点的连线与X 轴之间的夹角；θ为输电线路上任意一点的坡度.输电线路上任意一点的斜率y′为

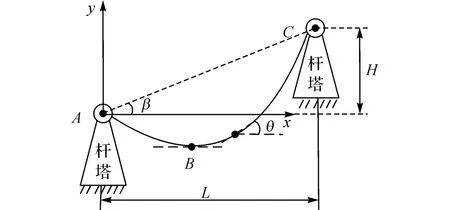
图3 输电线路建模示意图Fig.3 Diagram of transmission line’s mathematical model

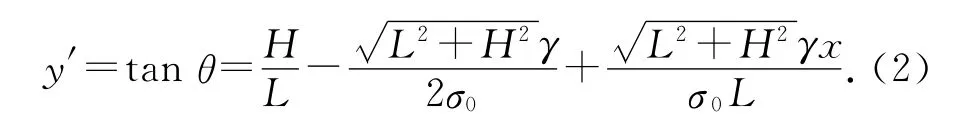
2.2 匀速行驶时的力学建模

在实际线路中，一个档段（即相邻杆塔之间的距离）会有几百米，而其中防震锤段不足半米.除了过防震锤段采用爬行越障，线路的其余部分均采用压紧关节（压紧轮）松开，行走关节（行走轮）滚动行驶的方式（目前机器人只在最大坡度小于35°的线路上运行）.在进行能耗预测时，可以近似将整个越障行驶方式看作是压紧关节（压紧轮）松开，行走关节（行走轮）滚动的行驶方式.

1）当机器人上坡行驶时的力学建模.

由于巡视机器人两操作臂之间的距离远远小于输电线路的曲率半径，可以将两操作臂之间的输电线路近似为直线.力学建模［6］如图4所示，机器人采用双轮驱动，当上坡匀速行驶时，行走轮的滚动方向为顺时针方向，行走轮电机提供驱动力矩，力矩方向为顺时针，滚动摩阻的方向与运动方向相反为逆时针方向，摩擦力的方向与运动方向相同.

通过上述分析有以下公式：

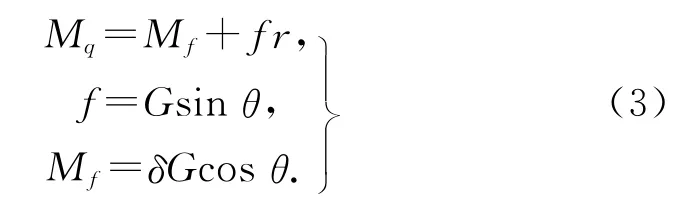
由式（3）可得

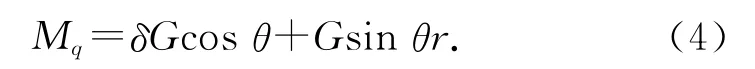
式中：Mq为巡视机器人在输电线路上行驶时，行走关节里面的直流电机提供的驱动力矩；f 为巡视巡视机器人在输电线路上行驶时，2个行走关节受到的摩擦力；Mf为机器人在输电线路上行驶时，2个行走关节受到的滚动摩阻；δ 为巡视机器人行走关节与输电线路之间的滚动摩阻系数；G 为巡视机器人的重力；r为巡视机器人行走关节的内径.

图4 机器人上坡行驶时的力学建模示意图Fig.4 Mechanics model diagram when uphill

2）当机器人下坡行驶时的力学建模.

力学建模如图5所示.机器人采用双轮驱动，当下坡匀速行驶时，行走轮的滚动方向为顺时针方向，行走轮电机提供制动力矩，力矩方向与滚动方向相反为逆时针，滚动摩阻的方向与运动方向相反为逆时针方向，摩擦力的方向与运动方向相反.

通过上述分析有以下公式：

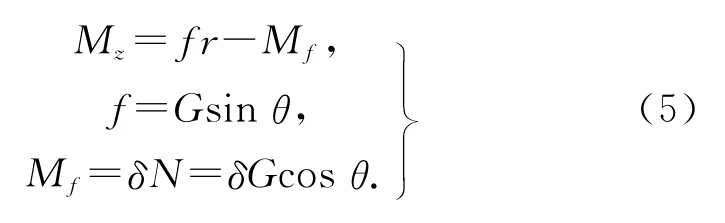
由式（5）可得

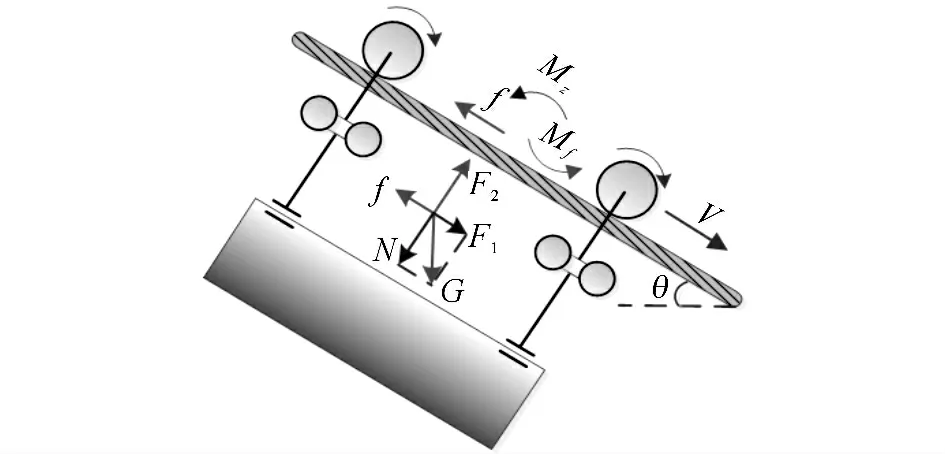
图5 机器人下坡行驶时的力学建模示意图Fig.5 Mechanics model diagram when downhill

2.3 基于输电线路环境参数的能耗建模

机器人在架空线路上行驶时的能耗W 可以看作由如下2部分组成：一部分能耗为行走关节在输电线路上行驶时克服摩擦力和重力做功的能耗W′，另一部分能耗为机器人在线下空载转动的能耗（包含电气和机械损耗）W″.

1）克服摩擦力和重力做功的能耗为

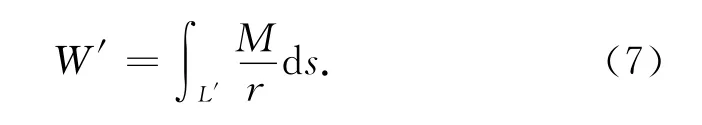
式中：L′为输电线路的弧长，M 为行走关节电机的输出力矩，r为行走关节的内径.

如图3中输电线路的数学模型所示，将曲线段AB 的弧长记为L′1，将曲线段BC 的弧长记为L′2，即有

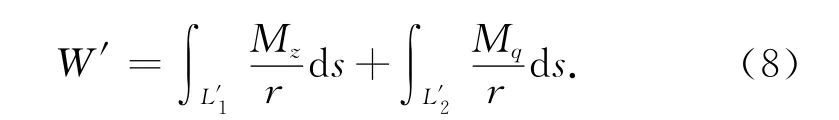
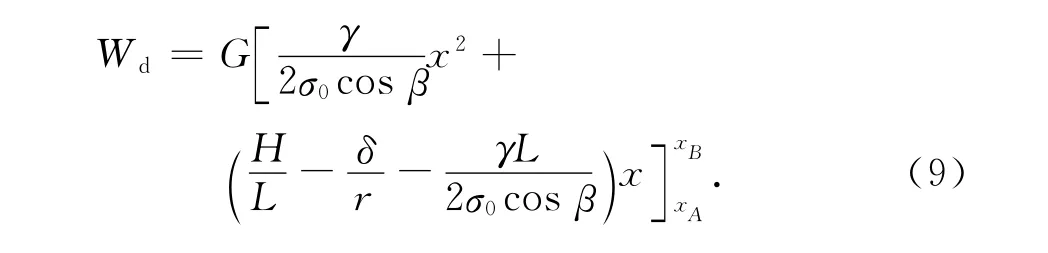
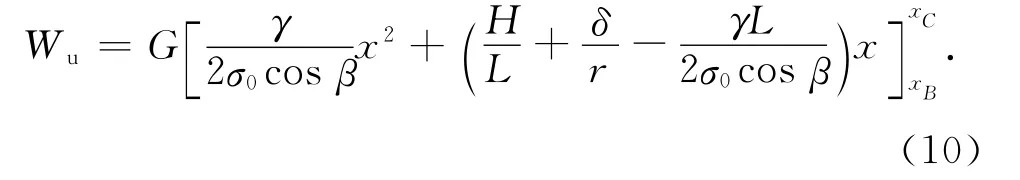
将式（9）、（10）代入式（8），可得行走轮所做的功为

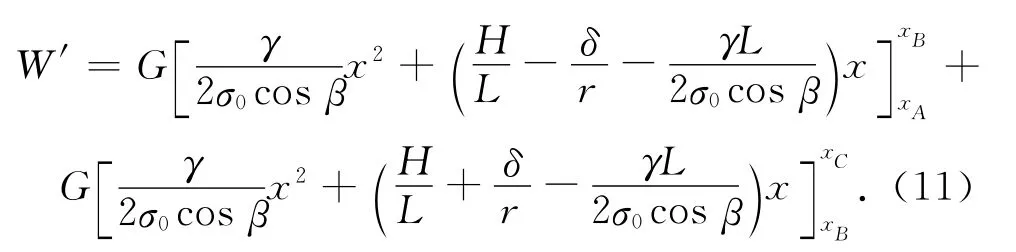
根据图3中输电线路的数学模型所示，可知图中A 点、B 点和C 点的横坐标分别为：xA＝0，xB＝L／2-σ0Hcosβ／（γL），xC＝L.将坐标代入式（11）可得行走轮克服摩擦力和重力做功的能耗：

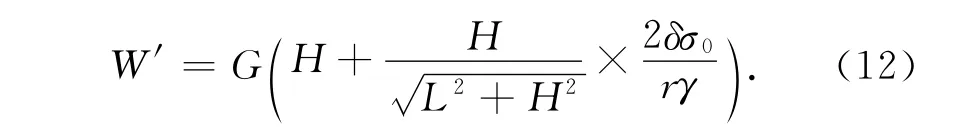
2）线下空载转动时的能耗W″为

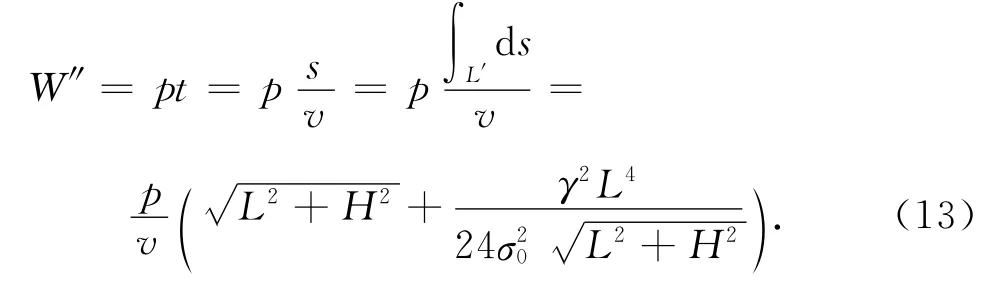
式中：p 为线下空载转动时的功率，为常量；v 为机器人匀速行驶时的速度.

由式（12）和（13）可得机器人的能耗公式为

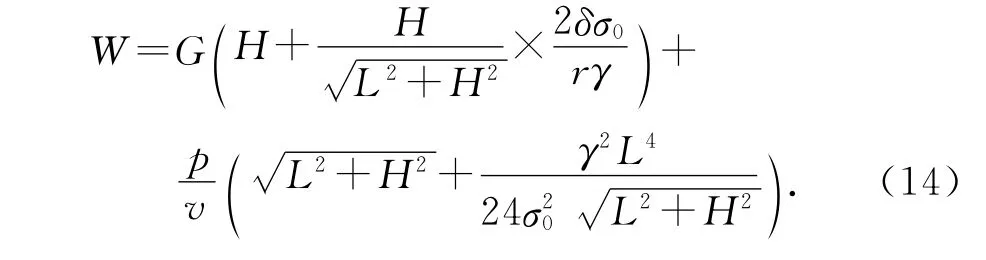
3 现场实验

图6 能耗的现场实验Fig.6 Field experiment of energy comsumption

现场实验如图6所示.在连续14组相邻直线杆塔档段进行能耗实验，用L 表示档段的档距即相邻杆塔的水平距离，用H 表示相邻杆塔之间输电线路两悬点的高差，用W 表示每个档段所需能耗的理论值，用Wt表示通过机器人监控系统监测得到的实测值.通过巡视机器人中的电压和电流传感器采集数据获得机器人能耗Wt的方法如下：首先以5s为一单位周期采集电源的干路电流和端电压，电流、电压和单位周期（5s）相乘得到单位周期内的能耗；然后对行驶完每一档段所有单位周期内的能耗进行累加得到每一档段的能耗Wt.

14组相邻直线杆塔档段能耗的理论值W 和测量值Wt如表1所示.表中，e为相对误差.理论能耗模型中用到的相关参数如下：行走关节与输电线路的滚动摩阻系数为0.347mm；行走关节的内径为66 mm；常温下输电线路GJ50最低点的应力即水平应力σ0为317.48 MPa，输电线路的比载γ 为81.62×10-3MPa／m；巡视机器人的重力为413.85N；线下空载转动的功耗为181.82 W，机器人以0.83m／s的速度匀速行驶.

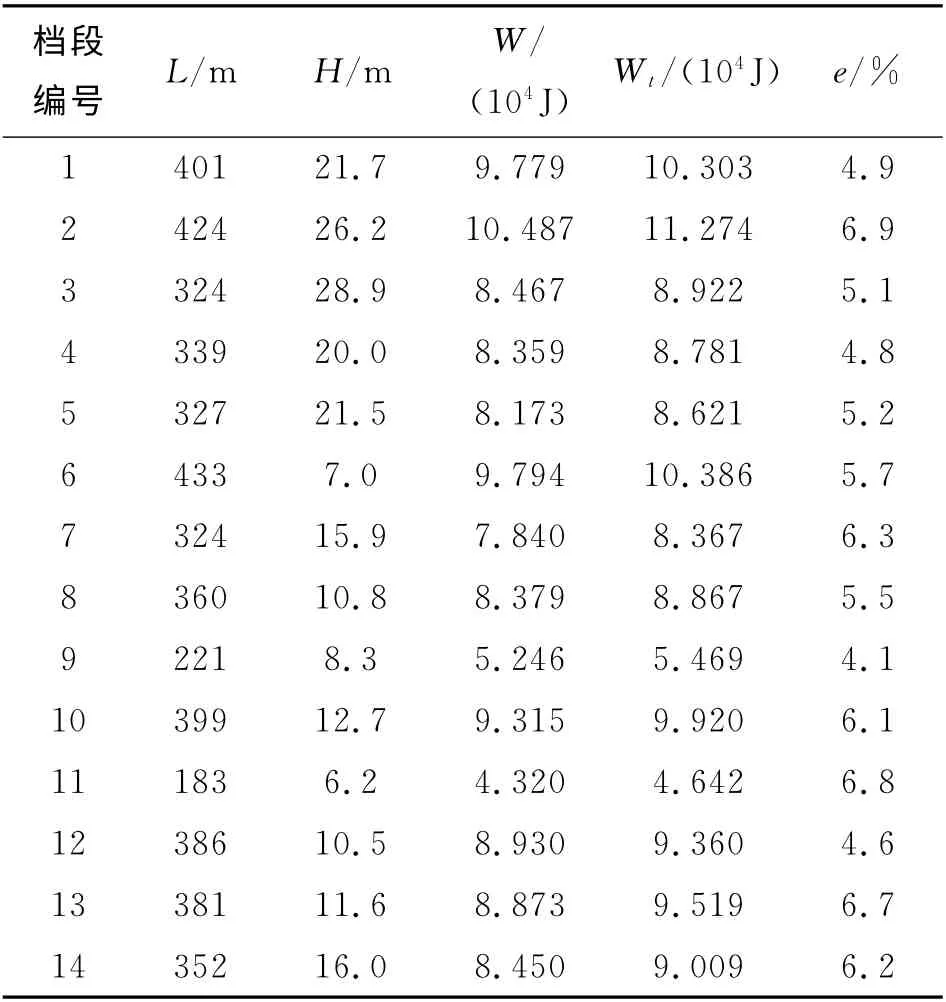
表1 单档段能耗理论值和测量值Tab.1 Theory value and measured value of energy consumption crossing two adjacent towers

图7 截止到第k个杆塔的能耗示意图Fig.7 Diagram of energy consumption from 0＃tower to k＃tower

根据表1的实验数据，得到从0＃杆塔依次截止到n＃杆塔（1≤n≤14）的能耗理论值和测量值的相对误差，如图8所示.可以看出，相对误差变动未知并且有增大的趋势，相对误差从最初的4.9%上升到了5.55%.为了更精确地估计xk，需要一种科学精确的估算方法.

本文在基于能耗模型的基础上，通过自适应卡尔曼滤波对能耗进行更加准确的估计.

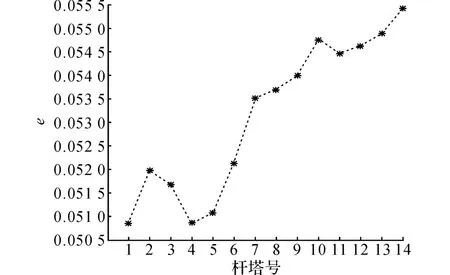
图8 能耗理论值与测量值的相对误差Fig.8 Relative error between theory value and measured value of energy consumption

4 自适应卡尔曼滤波

卡尔曼滤波的基本原理如下.如图9所示，以截止到n-1杆塔的能耗的最优估计为准，依据系统的状态方程，预测截止到杆塔n 的能耗x，同时对状态进行观测，得到观测能耗Zn；再在预测与观测之间进行分析，或者说以观测量对预测量进行修正，从而得到杆塔n 的最优状态估计.通过不断的迭代修正，使最优状态估计值逐步逼近测量值，提高了估计精度.

因为建立的基于工况参数的能耗模型含有变动未知的误差，本文采用带模型误差系统的自适应滤波器［7-10］.建立滤波器需要的状态方程和量测方程如下.

1）状态方程为

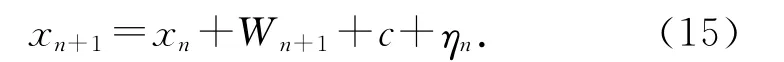
式中：Wn表示机器人巡检完第n个档段（即第n-1＃杆塔至第n＃杆塔之间的输电线路）所需的理论能耗，

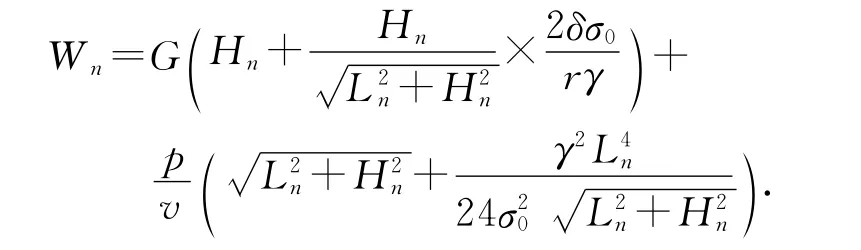
由于能耗模型中的理论值与测量值总是负偏差，在式（15）中加入常数项c，c为常数项5 020（J），为14组能耗估计值Wn和测量值Wtn之间的绝对误差均值；ηn 为虚拟噪声，其均值μη（n）和方差Q（n）随档段的变化而变化.

2）量测方程为

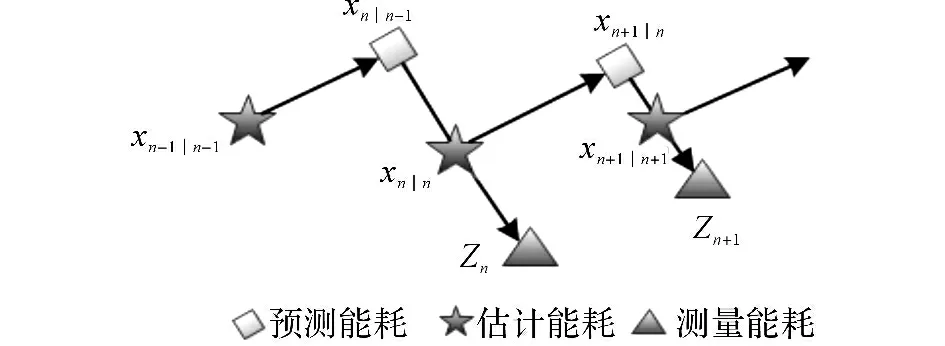
图9 卡尔曼滤波的基本原理Fig.9 Basic principle of Kalman filter

根据建立的状态方程和量测方程，可得带有模型误差系统的卡尔曼自适应滤波器方程为

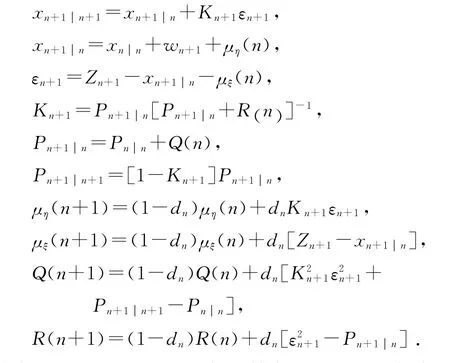
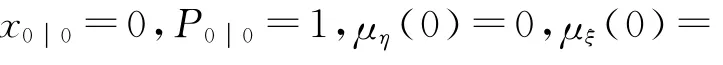
经过14次的迭代修正，误差稳定在1.05%左右，提高了估计精度.然后将14＃～k＃中间所有的档段整个看作下一段，通过建立的自适应卡尔曼滤波器，可以更准确地估计从起始杆塔到预定杆塔所需要的能耗.

图10 能耗的估计值和测量值Fig.10 Estimated value and measured value of energy consumption

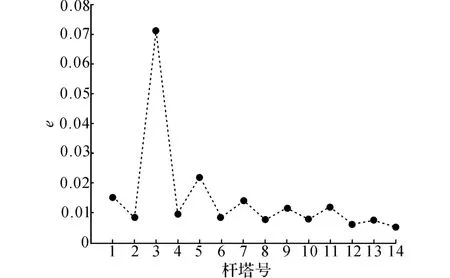
图11 估计值和测量值的相对误差Fig.11 Relative error between estimated value and measured value

5 结 语

本文首先建立沿地线穿越越障机器人基于线路环境参数的能耗模型.根据该能耗模型，建立带有模型误差系统的卡尔曼自适应滤波器所需的状态方程，经过卡尔曼滤波器的迭代修正，提高了能耗的估计精度.在日后的巡检过程中，只要给定线路的工况参数（水平档距、档段高差、线路型号等），就可以预估机器人所需的能耗，而不会导致机器人盲目巡检，因电量不足而停在档段中央以及无法到达预定杆塔，从而造成巡检事故，解决了机器人在实用化过程的一个关键性技术问题，为机器人的安全巡检提供了理论支撑.

（

）：

［1］吴功平，肖晓晖，肖华，等.架空高压输电线路巡线机器人样机研制［J］.电力系统自动化，2006，30（13）：90-107.WU Gong-ping，XIAO Xiao-hui，XIAO Hua，et al.Development of a mobile inspection robot for high voltage power transmission line［J］.Automation of Electric Power System，2006，30（13）：90-107.

［2］石璞，董再励.基于UKF滤波的自主移动机器人锂电池SOC估计［J］.仪器仪表学报，2006，27（6）：1298-1299.SHI Pu，DONG Zai-li.UKF-based SOC estimation of Li-ion battery for autonomous mobile robot［J］.Chinese Journal of Scientific Instrument，2006，27（6）：1298-1299.

［3］林成涛，陈全世，王军平，等.用改进的安时计量法估计电动汽车动力电池SOC［J］.清华大学学报：自然科学版，2006，46（2）：247-251.LIN Cheng-tao，CHEN Quan-shi，WANG Jun-ping，et al.Improved Ah counting method for state of charge estimation of electric vehicle batteries［J］.Journal of Tsinghua University：Science and Technology，2006，46（2）：247-251.

［4］高明煜，何志伟，徐杰.基于采样点卡尔曼滤波的动力电池SOC 估计［J］.电工技术学报，2006，26（11）：161-167.GAO Ming-yu，HE Zhi-wei，XU Jie.Sigma point Kalman filter based SOC estimation for power supply battery［J］.Transactions of China Electrotechnical Society，2006，26（11）：161-167.

［5］孟遂民.架空输电线路设计［M］.北京：中国电力出版社，2007：67.

［6］朱兴龙，王洪光，房立金，等.输电线路巡视机器人行走动力特性与位姿分析［J］.机械工程学报，2006，42（12）：143-150.ZHU Xing-long，WANG Hong-guang，FANG Li-jin，et al.Analysis of drive dynamic performance and positionpose of autonomous robot for transmission line inspection ［J］.Chinese Journal of Mechanical Engineering，2006，42（12）：143-150.

［7］刘胜，张红梅.最优估计理论［M］.北京：科学出版社，2011：273-275.

［8］GREGORY L P.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs Part1.background［J］.Journal of Power Sources，2004，134（2）：252-261.

［9］NOVIE A W，JAEHO C.LiPB battery SOC estimation using extended Kalman filter improved with variation of single dominant parameter［J］.Journal of Power Electronics，2012，12（1）：40-48.

［10］ZHANG Fei，LIU Guang-jun，FANG Li-jin，et al.Estimation of battery state of charge with H∞observer：applied to a robot for inspecting power transmission lines［J］.IEEE Transactions on Industrial Electronics，2012，59（2）：1086-1095.