大尺寸空间测量中转站误差分析与估计

金涨军，李江雄，俞慈君，柯映林

（浙江大学 机械工程系，浙江 杭州310027）

飞机装配是整个飞机制造过程中最重要的环节，装配劳动量占整个飞机制造劳动量的50%以上，是决定飞机质量的关键工艺流程［1］.为了提高飞机装配的精度，现代飞机装配技术大量使用了高精度的大尺寸测量设备，比如激光跟踪仪［2］.由于大飞机部件以及现场工装设备的遮挡，单台激光跟踪仪无法在一个站位完成对整个装配对象的测量.因此，需要采用多台激光跟踪仪协同工作或者单激光跟踪仪多站位的工作方式来满足飞机装配现场的测量任务需求.为了便于测量结果和飞机数模直接比较，来自不同（或不同站位）激光跟踪仪的测量数据需要转换到统一的飞机装配坐标系下.建立激光跟踪仪测量坐标系到飞机装配坐标系的转换关系的过程称为转站.转站是通过测量一组公共观测点进行匹配实现的，目的是获得从激光跟踪仪测量坐标系到装配坐标系的坐标转换参数（转站参数）.SVD 分解法［3-4］、正交矩阵法［5］、四元数法［6］是常用的求解 刚体匹配问题的解析算法，此外还有耿娜等［7-8］提出的基于刚体运动理论和模式搜索的坐标系匹配算法.

在转站过程中，公共观测点的测量误差会导致转站误差，转站误差是决定大尺寸测量精度的最主要的因素之一.部分学者针对大尺寸测量中的转站精度问题展开了研究.Calkins等［9-10］建立统一的空间测量网络（USMN）模型，提出测量点综合不确定度的加权评定算法，对大尺寸转站测量中的转站参数进行优化，该方法已应用到SA 软件中.Mitchell等［11］以各测量设备的测量协方差矩阵和雅可比矩阵为依据，按照矩阵加权线性最小方差为最优融合准则，提高不同测量设备数据的坐标转换精度.张福民等［12-14］采用蒙特卡洛仿真方法和现场实验方法对该方法进行验证.Predmore［15］通过建立测量点的不确定度椭球误差模型，提出一种基于参考点马氏距离最小的转站方法来提高转站精度.张春富等［16］用实验统计方法对激光跟踪仪的转站测量不确定度进行分析.林嘉睿等［17］利用激光跟踪仪极高精度的测距值作为约束，对跟踪仪测角误差进行优化，提高大空间三维坐标控制的精度.以上方法都是针对特定的测量系统配置通过对转站参数值进行优化来提高转站的精度，没有分析转站参数误差的不确定度对坐标转换精度的影响.

为了评价大尺寸测量的不确定度，笔者根据激光跟踪仪转站的基本原理，建立一种描述转站参数误差和转站误差的数学模型.该模型揭示了转站参数误差、转站误差与公共观测点布局、激光跟踪仪测量误差之间的数学关系.基于该模型实现了对转站参数误差的不确定度评定和对转站误差的估计.采用蒙特卡洛方法对激光跟踪仪转站进行模拟，验证了本文提出的转站参数误差不确定度评定方法和转站误差估计方法的合理性.

1 激光跟踪仪转站原理

在飞机装配现场，由于飞机部件相对较大的尺寸和各种装配工装的遮挡，需要采用多台激光跟踪仪或单激光跟踪仪多站位的配置方法来完成飞机装配过程的测量任务.每台激光跟踪仪具有独立的测量坐标系，因此来自不同激光跟踪仪或者不同站位的同一台激光跟踪仪的测量数据需要被转换到统一的装配坐标系下.激光跟踪仪转站的目的是获取跟踪仪在不同工作位置时测量坐标系到装配坐标系的转换参数.转站是通过测量一组空间分布的公共观测点来完成的，如图1所示.公共观测点是整个装配系统的基准，为了能够方便地实现转站和保证测量的精度，它需要被合理地布置以包围整个测量空间.

激光跟踪仪转站的本质是三维点组的刚体匹配问题.假设公共观测点在装配坐标系下的理论坐标为yi，在激光跟踪仪测量坐标系下为xi.转站参数用T（x，y，z）和R（α，β，γ）来表示，其中T 表示激光跟踪仪测量坐标系相对于装配坐标系的平移参数，R 表示激光跟踪仪测量坐标系相对于装配坐标系的旋转参数，α、β、γ为相应的RPY 角.

由于公共观测点之间的相对位置是固定不变的，每一个公共观测点的测量值yi和xi之间存在一个刚性的几何变换关系，即

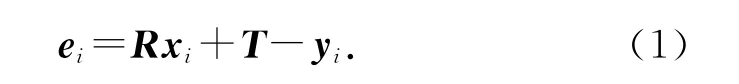
式中：ei为第i 个公共观测点的测量误差引起的转站误差.

为了求解最佳的转站参数R 和T，构建所有公共观测点的转站误差（RE）的最小二乘函数：

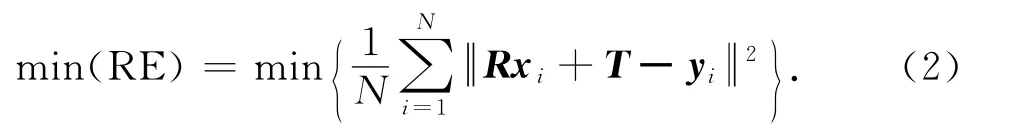
式中：N 为参与转站的公共观测点的数量.

对于式（2），可以使用SVD 分解法求解转站参数.在获得转站参数后，装配空间内任意检测点的测量值均可以实现在装配坐标系下表述：

图1 多站位激光跟踪仪测量原理Fig.1 Measurement principle of multiple laser trackers

转站参数R 和T 的误差是决定现场大尺寸测量的精度的重要因素.由于转站的过程只能获得一次转站中的转站参数，很难通过统计的方法获得转站参数误差的不确定度.

2 转站误差和转站参数误差分析

由于激光跟踪仪对公共观测点的测量存在随机误差，不同的公共观测点参与转站会产生不同的转站参数误差.转站参数误差的不确定度是衡量现场测量精度的重要指标.在不考虑温度、振动等环境因素的情况下，公共观测点作为固定的参考基准，它在装配坐标系下的参考值是固定不变的.假设yi表示公共观测点在装配坐标系下的理论真值，xi和Δxi分别为公共观测点在激光跟踪仪测量坐标系下的理论测量值和测量误差，Δxi服从均值为零、协方差矩阵为Σxi的正态分布.于是，转站误差［18-19］表示为

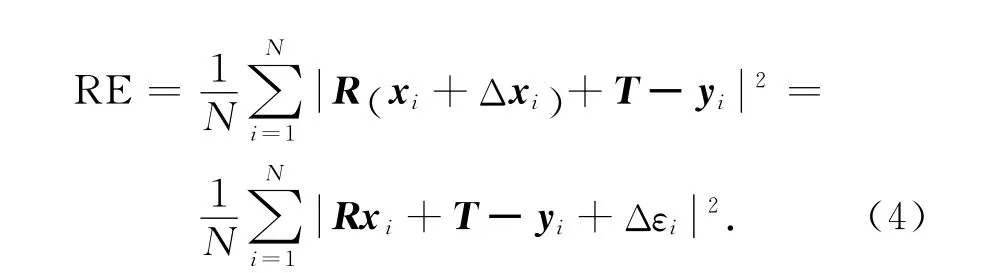
式中：Δεi＝RΔxi，Δεi服从正态分布：

当不存在测量误差时，两组数据点完美匹配：

式中：R0和T0为理论的转站参数.

将式（5）代入式（4），则转站误差为

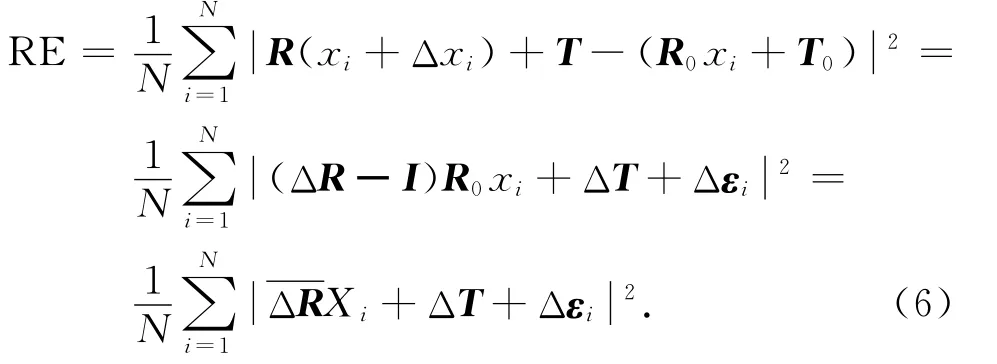
式中：

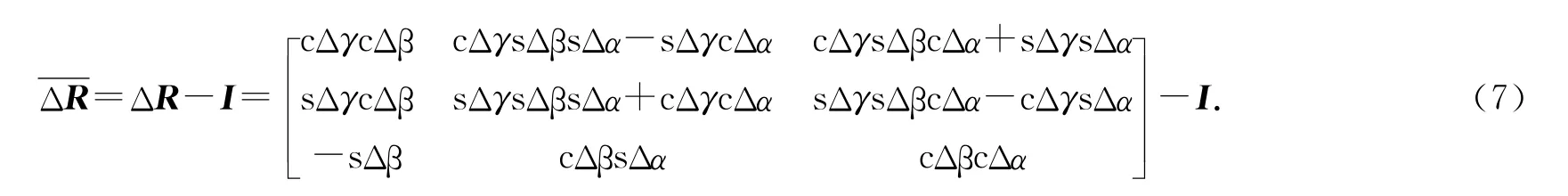
其中：cx＝cos（x），sx＝sin（x），Δα、Δβ、Δγ 为旋转参数误差；ΔT＝T-T0＝ ［Δtx，Δty，Δtz］T是平移参数误差，Xi＝R0xi.

由于激光跟踪仪测量精度很高，转站参数误差相对于转站参数来说是高阶无穷小量，旋转参数误差矩阵可以表示为一阶泰勒近似：

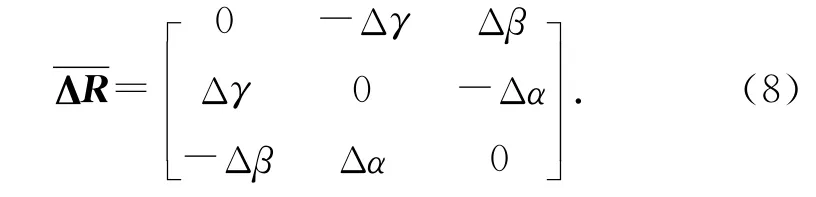
式（6）中等式右边第1项表示由于旋转参数误差引起的转站误差，第2项表示由平移参数误差引起的转站误差，第3项表示由于激光跟踪仪测量误差引起的转站误差.

式（6）的最小化问题实际上与求解下列方程组的最小二乘解是一致的.

将式（9）展开后，可以得到一共包含3 N 个方程的线性方程组：

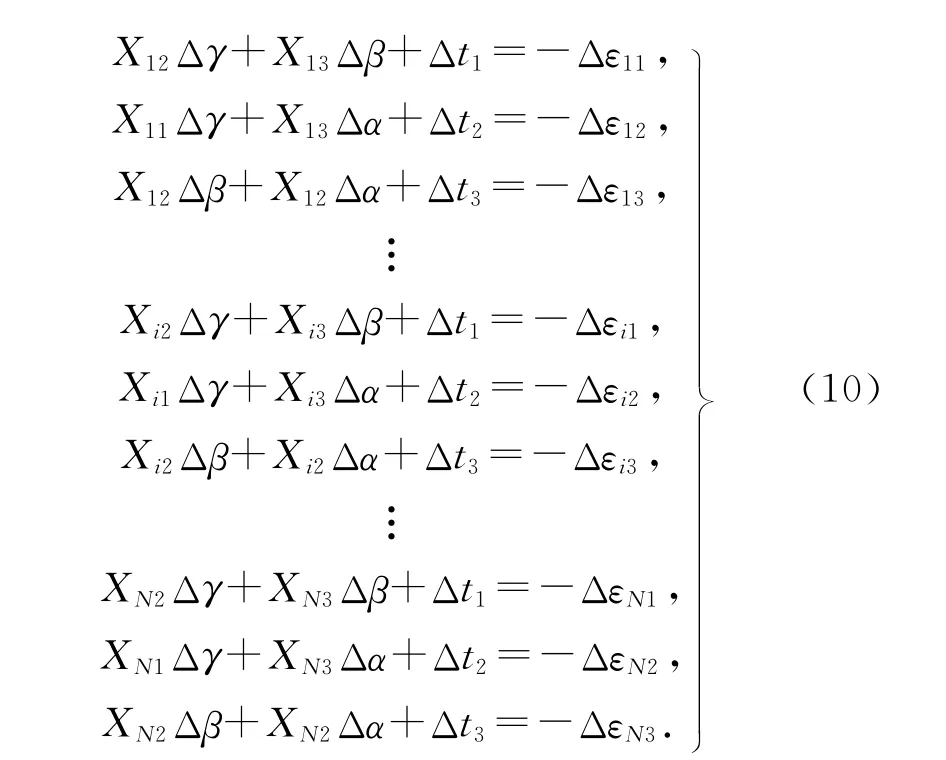
式中：Xik为Xi的第k 个分量；Δεik为Δεi的 第k 个分量，k＝1，2，3.

定义公共观测点配置矩阵：

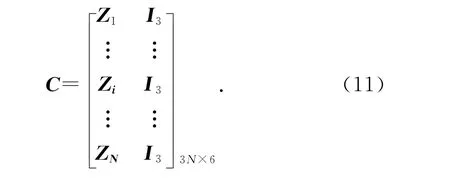
式中：

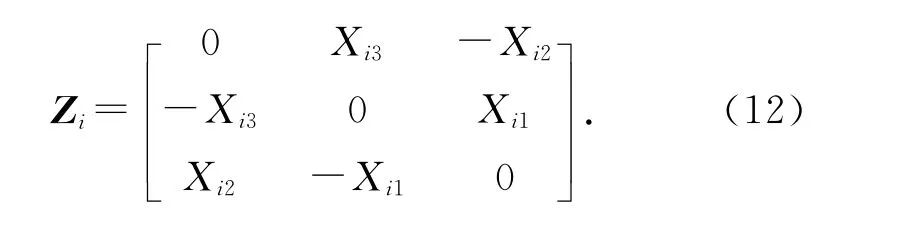
方程组（10）可以通过矩阵形式来表示：

式中：q为转站参数误差矩阵，

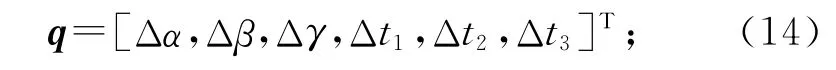
e为公共观测点测量误差矩阵，

通过对矩阵C 进行奇异值分解可得

于是，线性方程组的有效解为

式中：

Λ＋是一个6行3 N 列的矩阵，其元素满足

此时，转站参数误差和转站误差取得最小值.转站误差可以表示为如下的矩阵形式：

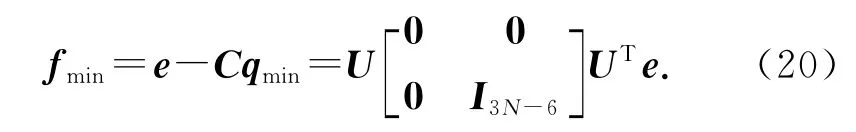
通过式（17）、（20）可知，转站参数误差和转站误差是由公共观测点的布局和激光跟踪仪对公共观测点的测量误差决定的.不同的公共观测点布局、不同的测量误差都会产生不同的转站参数误差.式（17）、（20）可以在测量系统设计阶段用来指导优化公共观测点的布局.

3 转站误差和转站参数误差不确定度估计

激光跟踪仪对公共观测点的测量误差是随机变量，因此转站参数误差和转站误差是随机变量.对转站参数误差和转站误差进行不确定度评估，可以定量地评价转站精度的高低.不确定度是用来描述测量结果分散性的物理量，它通过被测量的标准差σ予以量化.不确定度定义了一个置信区间，测量真值以一定的置信概率落在该区间中.对于正态分布的随机误差，常用的置信区间为1σ（置信概率68%）、2σ（置信概率95%）、3σ（置信概率99%）.根据评定方式的不同，不确定度可以分为A 类和B类不确定度.A 类不确定度是通过对一组大量的测量值进行统计分析，计算得到的标准差；B类不确定度是通过查阅标定报告或数据手册等资料中给出的被测量的标定值得到.无论是A 类不确定度还是B类不确定度，都可以通过合成得到复杂被测量的不确定度.

3.1 合成标准不确定度

假设目标被测量y 是通过一些输入变量xi的测量而间接得到的，被测量y 和输入变量xi之间满足如下关系式：

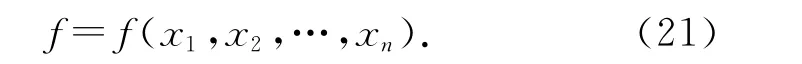
若各输入量xi（i＝1，2，…，n）无关，则y 的合成标准不确定度uc（y）可以由输入变量的标准不确定度u（xi）通过下式合成得到：

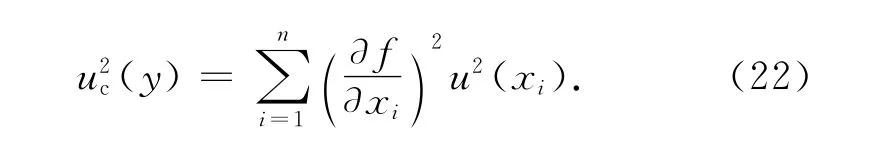
式中：偏导数∂f／∂xi为灵敏度系数，表示u（xi）变化单位量时引起的合成不确定度的变化值.

当目标被测量y是一个多维向量时，

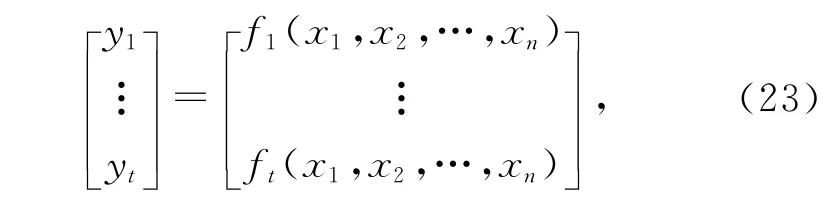
则y合成标准不确定度可以由下式计算得到：

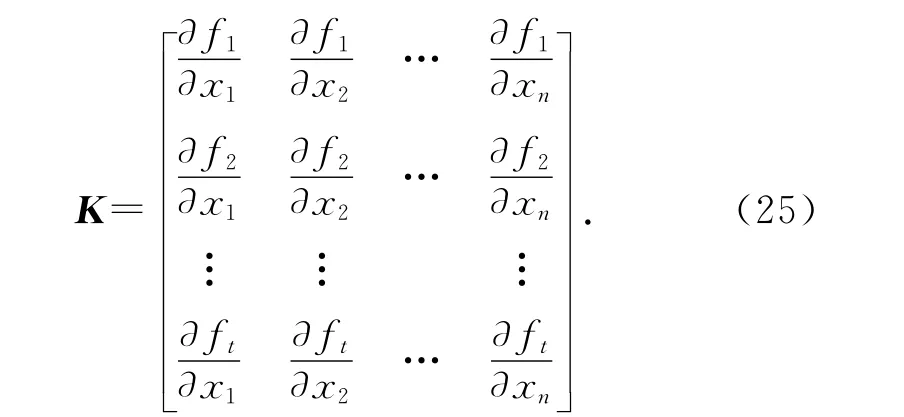
式中：Dx和Dy为输入变量x 和被测量y 的方差-协方差矩阵；K 为一个t行n 列的灵敏度系数矩阵，

3.2 转站参数误差的不确定度

由式（17）可知，转站参数误差是由公共观测点配置矩阵和公共观测点测量误差耦合的线性函数.根据不确定度合成原理可知，转站参数误差的合成标准不确定度为

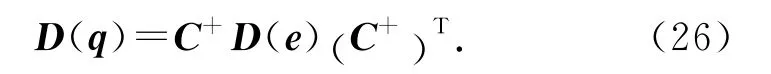
式中：D（e）为公共观测点测量误差矩阵e的方差-协方差矩阵，D（q）为转站参数误差q的方差-协方差矩阵.

3.3 转站误差估计

转站误差是由每一个公共观测点的匹配误差组成，第i个公共观测点的匹配误差表示为

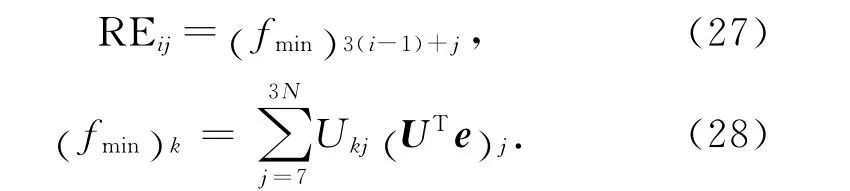
式中：i为公共观测点的编号，i＝1，2，…，N；j分别表示x、y、z方向的分量，j＝1，2，3.

根据式（28）可以得到每个公共观测点匹配误差分量之间的方差-协方差：

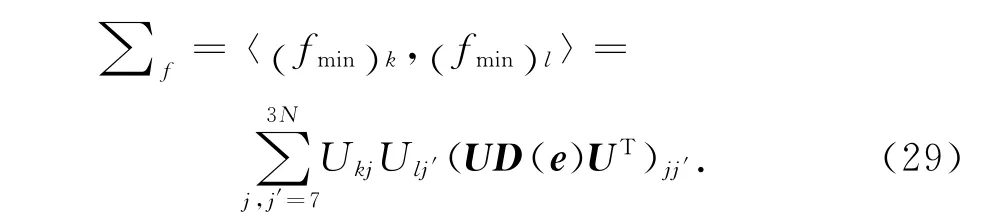
转站误差为各个公共观测点匹配误差不确定度的和的平均值：

4 蒙特卡洛仿真实验

采用蒙特卡洛方法对激光跟踪仪转站过程进行模拟，对本文提出的转站误差传递模型和转站参数误差、转站误差的不确定度估计方法的合理性进行验证.蒙特卡洛法是以数理统计的抽样理论为基础的计算机数值模拟方法.蒙特卡洛仿真的基本过程如下：首先构建激光跟踪仪转站过程中的误差分布模型，然后针对该模型进行随机取样产生大量的样本数据，最后用样本的统计结果作为转站结果的近似解.一般而言，蒙特卡洛模拟需要产生大量的样本数据，样本量越大，模拟结果越接近真值.

共设置13个激光跟踪仪站位，它们分别对应不同平移参数和旋转参数的组合，如表1所示.分别对每一个站位进行模拟转站，检验不同的站位参数对于提出的不确定度估计方法的效果.

表1 激光跟踪仪站位Tab.1 Location of laser tracker

在仿真过程中，选择9个公共观测点作为装配坐标系的参考基准，它们的理论坐标列举在表2中.

4.1 激光跟踪仪测量误差模型

为了实现激光跟踪仪转站的蒙特卡洛仿真，必须建立激光跟踪仪的测量误差模型.激光跟踪仪是一个典型的球坐标测量系统，它的三坐标测量值是跟踪仪传感器变量θ＝［α ，β，d ］T的复合函数：

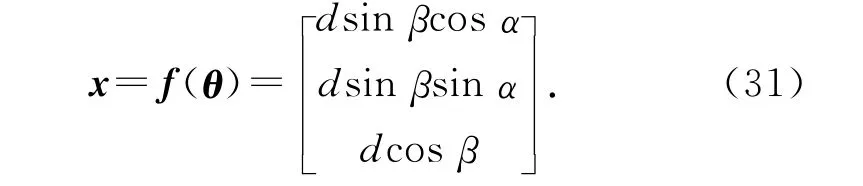
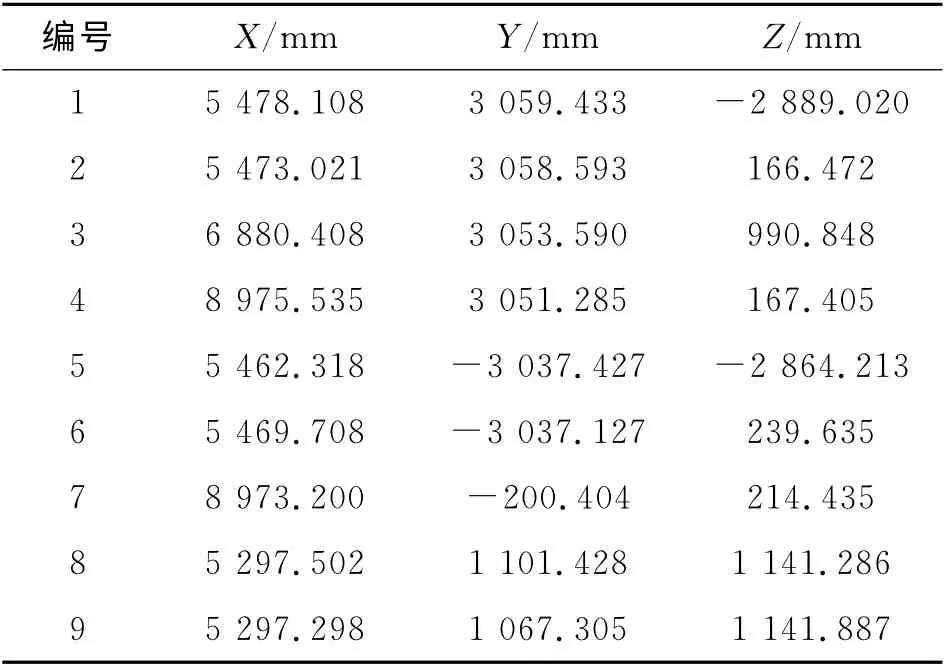
表2 公共观测点理论坐标值Tab.2 Nominal coordinates of ERS points

式中：α和β 为激光跟踪仪的水平角传感器和垂直角传感器的读数，d 为测量点的激光干涉距离.

激光跟踪仪工作时，无论是角度传感器还是激光干涉仪都存在一定的误差.当传感器变量存在较小的测量误差δθ 时，激光跟踪仪的测量误差［12］可以近似表示为

式中：J（θ）为雅各比矩阵，

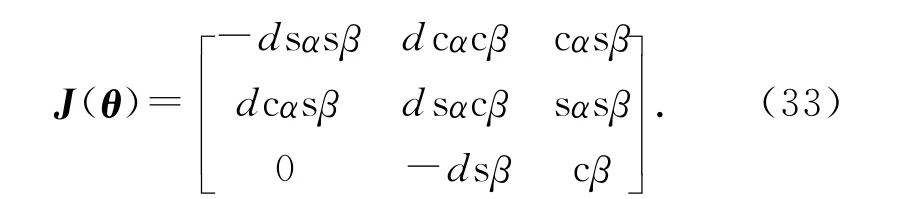
根据Leica公司的激光跟踪仪AT901-LR的技术参数可知，距离测量精度为±0.5×10-6，角度传感器的测量精度为±（15×10-6m＋6×10-6）.

4.2 仿真实验步骤

对每个激光跟踪仪站位执行如下实验步骤.

1）构建当前跟踪仪站位下对应的转站参数的理论旋转矩阵和平移矩阵分别为R 和T，计算公共观测点在跟踪仪坐标系下的理论测量值.

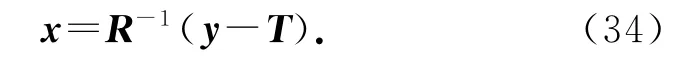
2）模拟激光跟踪仪转站过程10 000次.

a）根据式（31）反向求解每个公共观测点对应的激光跟踪仪的传感器变量θ，计算J（θ）.

b）使用随机噪声δθ模拟每个公共观测点的激光跟踪仪传感器测量误差，其中角度传感器误差δα和δβ服从均值为0、标准差为u（α）和u（β）的正态分布；距离误差δd 服从均值为0、标准差为u（d）的正态分布.

c）根据式（32）计算每个公共观测点的测量误差Δx.

d）计算公共观测点的实际测量值：

e）对带有测量误差的测量值x′和理论值y 进行匹配运算，用SVD 法求解转站参数，并计算转站误差.

3）对10 000次转站数据进行统计，计算转站参数误差的标准不确定度s和转站误差的平均值.

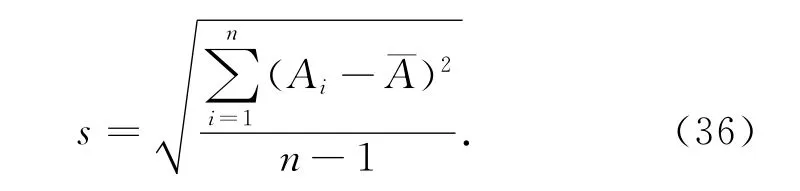
4）根据式（26）和（30），计算每一个站位的转站参数误差不确定度估计值和转站误差估计值.

5）对每个站位的估计结果和仿真结果进行比较，检验本文提出的转站误差估计和转站参数误差不确定度估计方法的准确性.

4.3 实验结果

通过蒙特卡洛仿真实验，分别对本文提出的转站参数误差不确定度估计方法和转站误差估计方法的合理性进行验证.

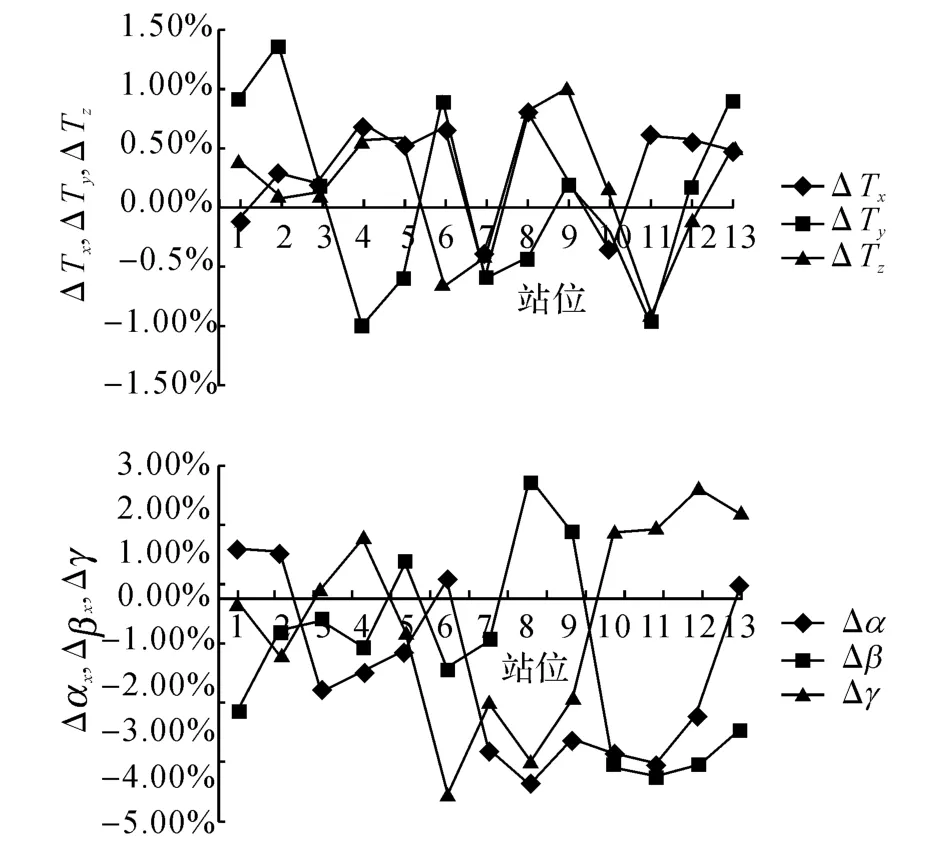
图2 转站参数误差不确定度估计的相对误差Fig.2 Relative estimation errors of transformation parameter errors

如图2所示为激光跟踪仪在每个站位转站过程中平移参数误差和旋转参数误差的不确定度的相对估计误差.可以看出，本文方法对平移参数误差的平均估计误差为0.53%，最大估计误差为1.37%；对旋转参数误差的平均估计误差为2.02%，最大估计误差为4.38%.从结果来看，平移参数误差的估计精度高于角度参数误差的估计精度.

如图3所示为每个站位的激光跟踪仪转站误差的相对估计误差.从图3可知，本文方法对转站误差的估计是非常准确的，平均估计误差为0.34%，最大估计误差仅为0.71%.

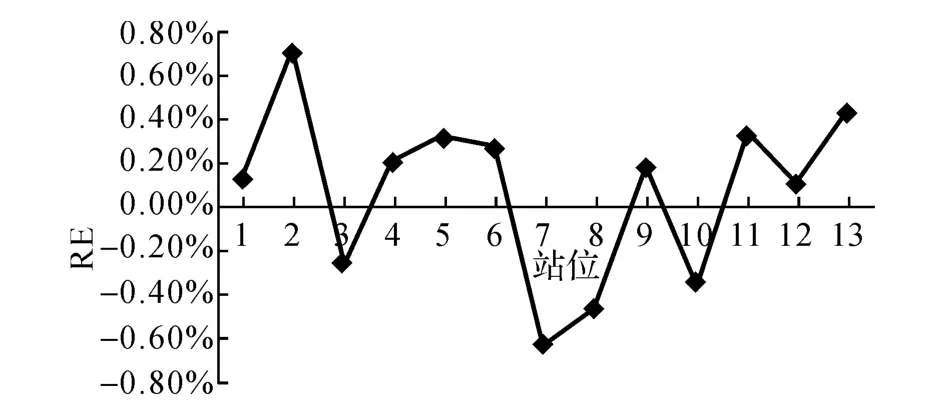
图3 转站误差估计的相对误差Fig.3 Relative estimation error of registration error

5 结 语

针对激光跟踪仪的转站测量原理，本文建立一种描述转站参数误差和转站误差的数学模型.该模型揭示了公共观测点布局和激光跟踪仪测量误差对转站精度的影响.基于该模型，提出一种转站参数误差不确定度的评价方法和转站误差的估计方法.通过蒙特卡洛仿真实验对本文方法进行验证.实验结果证明，本文方法对平移参数误差的最大估计误差为1.37%，对旋转参数的最大估计误差为4.38%，对转站误差的最大估计误差为0.71%.

（

）：

［1］邹冀华，刘志存，范玉青.大型飞机部件数字化对接装配技术研究［J］.计算机集成制造系统，2007，13（7）：1367-1373.ZHOU Ji-hua，LIU Zhi-cun，FAN Yu-qing.Large-size airplane parts digital assembly technology［J］.CIMS，2007，13（7）：1367-1373.

［2］ESTLER W T，EDMUNDSON K L，PEGGS G N，et al.Large-scale metrology：an update ［J］.R Annal，2002，51（2）：587-609.

［3］ARUN K S，HUANG T S，BLOSTEIN S D.Leastsquares fitting of two 3-D point sets［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，1987，9（5）：698-700.

［4］UMEYAMA S.Least-square estimation of transformation parameters between two point patterns［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，1991，13（4）：376-380.

［5］BERTHOLD K P H.Closed-form solution of absolute orientation using unit quaternions［J］，Journal of the Optical Society of America A，1988，4（4）：629-643.

［6］BERTHOLD K P H，HUGH M H，NEGAHDARIPOUR S.Closed-form solution of absolute orientation using orthonormal matrices［J］.Journal of the Optical Society of America A，1988，5（7）：1127-1137.

［7］耿娜，邾继贵，劳达宝，等.基于刚体运动学的坐标系配准理论及算法［J］.传感技术学报，2010，23（8）：1088-1092.GENG Na，ZHU Ji-gui，LAO Da-bao，et al.Theory and algorithm of coordinate system registration based on rigid body kinematics［J］.Chinese Jornal of Sensors and Actuators，2010，23（8）：1088-1092.

［8］张春富，张军，唐文彦，等.一种基于模式搜索的大尺寸测量移站坐标转换方法［J］.计测技术，2003，23（6）：12-14.ZHANG Chun-fu，ZANG Jun，TANG Wen-yan，et al.A coordinate transformation method of moving the station of large scale measurement based on mode searching［J］.Aviation Metrology and Measurement Technology，2003，23（6）：12-14.

［9］JOSEPH M C，ROBERT J S.A practical method for evaluating measurement system uncertainty［C］∥Boeing Large Metrology Conference.Long Beach： ［s.n.］，2000.

［10］CALKINS J M.Quantifying coordinate uncertainty fields in coupled spatial measurement systems［D］.Blacksburg：Virginia Polytechnic Institute and State University，2002.

［11］MITCHELL J，SPENCE A，HOANG M，et al.Sensors fusion of laser tracker for use in large-scale precision metrology ［J］.Proceeding of SPIE Intelligent Manufacturing，2004，5263：57-65.

［12］张福民，曲兴华，叶声华.大尺寸测量中多传感器的融合［J］.光学精密工程，2008，16（7）：1236-1240.ZHANG Fu-min，QU Xing-hua，YE SHENG-hua.Multiple sensor fusion in large scale measurement［J］.Optics and Precision Engineering，2008，16（7）：1236-1240.

［13］张福民，曲兴华，叶声华.基于蒙特卡罗仿真方法的大尺寸测量不确定度分析［J］.计算机集成制造系统，2009，15（1）：184-196.ZHANG Fu-min，QU Xing-hua，YE Sheng-hua.Uncertainty analysis in large-scale measurement based on Monte Carlo simulation method ［J］.CIMS，2009，15（1）：184-196.

［14］张福民，曲兴华，戴建芳，等.一种现场大尺寸测量精度的评价方法［J］.光学学报，2008，28（11）：2159-2163.ZHANG Fu-min，QU Xing-hua，DAI Jian-fang，et al.A method of precision evaluation for field large-scale measurement［J］.Acta Optica Sinica，2008，28（11）：2159-2163.

［15］PREDMORE C R.Bundle adjustment of multi-position measurements using the Mahalanobis distance ［J］.Precision Engineering，2010，34（1）：113-123.

［16］张春富，张军，许文海，等.激光跟踪仪现场测量不确定度的评定［J］.计量学报，2005，26（1）：20-22.ZHANG Chun-fu，ZHANG Jun，XU Wen-hai，et al.Evaluation of site measuring uncertainty of laser tracker［J］.Acta Metrology Sinica，2005，26（1）：20-22.

［17］林嘉睿，邾继贵，郭寅，等.现场大空间测量中精密三维坐标控制网的建立［J］.机械工程学报，2012，48（4）：6-11.LIN Jia-rui，ZHU Ji-gui，GUO Yin，et al.Establishment of precise three-dimensional coordinate control network in field large-space measurement［J］.Journal of Mechanical Engineering，2012，48（4）：6-11.

［18］DANILCHENKO A，FITZPATRICK J M.General approach to error prediction in point registration［C］∥SPIE Medical Imaging International Society for Optics and Photonics.San Diego：［s.n.］，2010.

［19］WEST J B，FITZPATRICK J M.The distribution of target registration error in rigid-body point-based registration［J］.IEEE Transactions on Medical Imaging，2001，20（9）：917-927.