离散Boltzmann-BGK方程解的长时间特性研究
徐思齐
(信阳师范学院 土木工程学院, 河南 信阳 464000)
0 引言
为了避免流体力学中对于Navier-Stokes方程的求解,格子Boltzmann方法中利用BGK近似来代替碰撞过程,并通过求解离散速度的Boltzmann-BGK方程来模拟牛顿流体.Cabannes[1-2]研究了离散Boltzmann方程在零解附近的整体解的存在性,在此基础上,Beale[3]研究了离散Boltzmann方程解在时间t→∞时的渐近性质.之后,Kawashima[4]研究了在初值靠近绝对Maxwell量时,离散Boltzmann方程整体解的存在唯一性,并给出了该方程在时间t→∞时解的渐近形式.关于连续情形Boltzmann方程解的渐近行为可参阅文献[5-9].
本文对于离散速度Boltzmann-BGK方程的研究可以通过类似文献[4]中的方法,对其进行Chapman-Enskog展开[2],得到一阶近似的Euler方程,并对Euler方程的特征域进行分析,得出当时间t→∞时方程解的渐近形式.本文主要以D1Q3模型[10-11]为例,考察当t→∞,碰撞频率取ρ时,离散速度Boltzmann-BGK方程解的渐近性质.首先,通过平衡态分布函数的展开,整理D1Q3模型对应的方程,求得其对应的Euler方程,分析特征域的性质;然后,分析线性化方程组对应的特征值,并验证原方程组解的存在唯一性;最后,给出方程解的渐近形式.
1 Euler方程及其特征域分析
1.1 离散速度Boltzmann-BGK方程及求和不变量
D1Q3模型的离散速度Boltzmann-BGK方程的一般形式为:
(1)

且满足质量守恒与动量守恒:
ρ=∑fi,ρu=∑fiei,i=0,1,2.
对于D1Q3模型,
则方程组(1)可化为:
(2)
考虑其初值问题
(3)

1.2 Euler方程的推导

(4)
可得相应的Euler方程(σj)t+〈VF,ψj〉x=0,j=1,2,即:
(5)
1.3 特征域分析

证明条件(C1)的验证:若存在ψ∈M使得λψ=Vψ,∀λ∈R,则ψ可表示为ψ=c1ψ(1)+c2ψ(2),c1,c2∈R,其中ψ(1)=(1,1,1)T,ψ(2)=(0,1,-1)T为上述求和不变量集合M的一组基,代入λψ=Vψ,则有:
c1(λI-V)ψ(1)+c2(λI-V)ψ(2)=0.
由于
(λI-V)ψ(1)=(λ,λ-1,λ+1)T,
(λI-V)ψ(2)=(0,λ-1,-λ-1)T,
且这两个向量对于任意的λ∈R线性无关,故c1=c2=0,因此ψ=0.
条件(C2)的验证:Euler方程(5)式可改写为:
σt+A(σ)σx=0,
其中,
σ=(σ1,σ2)T=(ρ,m)T为F的矩,则A(σ)的特征值和相应的特征向量分别为:
因而,
则〈▽σλj(σ),rj(σ)〉≠0.即方程(5)的特征域在该区域中是完全非线性的.证毕.
2 解的整体存在及唯一性的验证
2.1 D1Q3方程的线性化
影响方程(1)中碰撞频率ω的因素为温度、密度以及介质的大小,本文考虑ω=ρ的情况,此时D1Q3方程(2)即为:
(6)
(7)
2.2 解的整体存在及唯一性定理
定理1(解的整体存在及唯一性定理) D1Q3模型满足条件(C1):对任意λ∈R,若存在ψ∈M满足λψ=Vψ,则ψ=0.令M是一个分量均为正的绝对Maxwell量.
(i)若F0-M∈Hs,s≥1且‖F0-M‖s值很小,则初值问题(2)和(3)具有唯一的整体解F(t,x),且F(t,x)满足F-M∈C0([0,∞);Hs)∩C1([0,∞);Hs-1).而且,当t→∞时,F(t,x)在Bs-1范数下收敛到M.
(ii)若F0-M∈Hs∩L1,s≥1且
Es=‖F0-M‖s+‖F0-M‖L1
很小,则对于t∈[0,∞),(i)中所描述的解F(t,x)满足
其中,0≤l≤s且C为一个常数.
注本定理的证明可参照文献[4].
3 解的渐近形式
3.1 线性方程特征值的谱表示
线性化方程(7)对应的特征矩阵为:

其特征值μ对应的特征方程为:
μ3+6μ2+ξ2μ+2ξ2=0,
(8)
作变换令μ=y-2,可得:
y3+(ξ2-12)y+16=0.
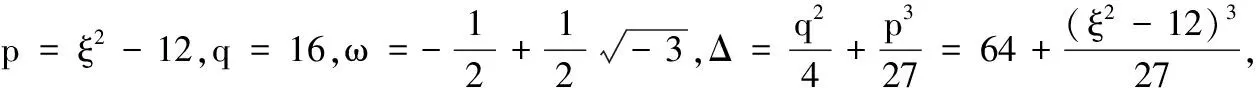
于是,方程(8)的解为μi=yi-2,i=1,2,3.易知,当iξ→0时,μ2→0,μ3→0,μ1不趋于0.

比较η,η2的系数,可得:
记:
(9)
3.2 解的渐近形式
在上述讨论的基础上,我们可以得到如下核心定理:


证明令zj(ρ,m)对于任意的(ρ,m)T都满足〈▽zj,rj〉=0,则可得到:

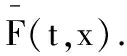
首先确定参数δj,j=1,2:
(10)
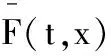

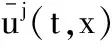
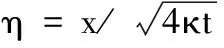
则所求的渐近解可由下面式(11)确定:
(11)
其中φ(1),φ(2)是ΛMM的基,可取φ(1)=(4,1,1)T,φ(2)=(0,1,-1)T.证毕.
4 结语
本文基于格子Boltzmann方法中的D1Q3模型,研究了一维离散速度的Boltzmann-BGK方程在绝对Maxwell量附近的整体解在长时间时具有的渐近形式,并且通过算子半群及双曲抛物系统中的理论,证明了此渐近解可由Burgers方程的自相似解叠加得到.

