解析Besov型空间
韩金桩,瑛 瑛
(呼伦贝尔学院 数学科学学院,内蒙古 呼伦贝尔 021008)
0 引言
设D={z∈C:|z|<1}表示单位圆盘,∂D={z∈C:|z|=1}表示单位圆盘D的边界.令H(D)表示D中所有解析函数组成的集合.
定义1[1]设0 则称f属于Hardy空间Hp,简记作f∈Hp,其中 定义2 令p>1和ρ:[0,1)→[0,+∞)是一权函数.若f∈H(D)满足 则称f∈Bp(ρ),其中dA(z)=π-1dxdy是D上规范化的勒贝格测度. 解析函数空间Bp(ρ)是Arcozzi、Rochberg和Sawyer引进的[2],它包含了很多重要的函数空间.设ρ(t)=ts,0≤s<∞,则空间Bp(ρ)和Besov型空间Bp(s)是相同的;特别地,如果s=0,则空间Bp(ρ)恰是经典的Besov空间Bp.当p=2时,则Bp(ρ)=Ds.关于Bp(s)空间可参阅文献[3-5].若权函数ρ满足某些条件,Arcozzi,Rochberg 和Sawyer 利用Carleson测度给出了Bp(ρ)空间的很多结论[2].Aleman证明了Dρ中每个元素是两个有界函数的商[6].参照文献[7]的考虑,设ρ:[0,∞)→[0,∞)是右连续的增函数且ρ满足 (1) 和 (2) 若条件(1)和(2)成立,由文献[7]的引理2.1和2.2,可得ρ有很多优美的估计,例如ρ是二阶可导的.根据文献[7],本文设ρ(0)=0,否则Bp(ρ)总是Besov空间Bp. 本文中符号A≈B意味着ABA,其中AB意味着存在一个常数C使得A≤CB. 性质1 设不等式(2)成立和1 证明给定一个f∈Bp(ρ),令0 因为不等式(2)成立,由文献[7]的引理2.2得,存在一个充分小的c使得t1-c≤ρ(t),所以 因此得 Mp(r,f-f(0)) 故有 证毕. 定义3 若f∈Lp(∂D)满足, 则称f∈Bp(ρ)(∂D). 令 (3) 为f的泊松积分. 引理1[9]设不等式(1)和(2)成立,则对任意的eit,eiu∈∂D,有 定理1 设不等式(1)和(2)成立,1 定理1的证明类似于文献[9]中引理3的证明方法,在此省略证明. 推论1 设不等式(1)和(2)成立,1 受Dyakonov在文献[10]中所做工作的启发,给出以下结论. 定理2 设不等式(1)和(2)成立,1 (1)f∈Bp(ρ); (2) (3) 证明(1)⟹(2).令 L1(r) 利用泊松积分公式, 因此,结合引理1,可得 利用同样的方法,可得 从而有 这就证明了(1)⟹(2). (1)⟹(3).令 同理,可得 L2(r) 这样,证明就类似于(1)⟹(2). (2)⟹(1). 由式(3),经简单计算得 |▽feit)| 因此, (3)⟹(1).该证明类似于(2)⟹(1).证毕. 推论2 设不等式(1)和(2)成立.令1 (1)f∈Bp(ρ); (2) (3) 推论2的证明方法类似推论1的证明,在此省略证明. 定义4 若I∈H(D)且满足 |I(eiθ)|=1,a.e.θ∈[0,2π], 则称I为内函数.设ln|g|∈L1(∂D),则称 为一个外函数,其中η∈∂D. 若函数f∈Hp,则f可分解成一个内函数和外函数的乘积.利用文献[4]的证明方法,易得下面的结论,在此省略证明. 定理3 设不等式(1)和(2)成立.令1 (1)f∈Bp(ρ); (2)I2(|f|)<∞且 设X⊂H1,I是一内函数.若对任意的h∈X,恒有h/I∈X,则称X具有f-性质. 推论3 设不等式(1)和(2)成立,1 证明结合定理3和 |f(z)|+f(z)(1-|I(z)|), 又因为|fI|∈Bp(ρ)(∂D)等价于I2(|fI|)<∞,利用基本的不等式,易得结论.证毕. 利用定理3可以证明,任意一个Bp(ρ)中的函数可以表示成Bp(ρ)中两个有界函数的商.下面的引理可见文献[6]的引理2.7. 引理2 令(X,μ)是一个概率测度空间,φ∈L1(X,μ)是一个非负函数且满足lnφ∈L1(X,μ).令 则E(min(1,φ))≤E(φ),E(max(1,φ))≤E(φ). 定理4 设不等式(1)和(2)成立,1 证明设f∈Bp(ρ)且f≠0(否则定理是显然的).由于Bp(ρ)⊂Hp,可以令f=IO,其中I和O分别是内函数和外函数.令 和 容易得到1/O+和O-位于H∞中.显然O=O+O-.注意到f=IO+O-=IO-/1/O+.设A=IO-且B=1/O+.下证A,B∈Bp(ρ).令 结合引理2,得到 E(|O+|,z)≤E(|O|,z), E(|O-|,z)≤E(|O|,z). 因此 E(|O|,z)≤ |O(z)|(1-|I(z)|)= E(|O-|,z)+|O-(z)|(1-I(z))≤ |O(z)|(1-|I(z)|)= 结合定理3,即可得证.证毕. 运用分析技巧和函数空间的若干知识,获得了解析型Besov型空间Bp(ρ)的两个解析特征,第一是函数在单位圆周上的积分特征;第二是Bp(ρ)中的函数可以分解为两个有界解析函数的商.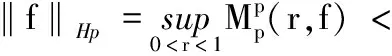

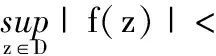



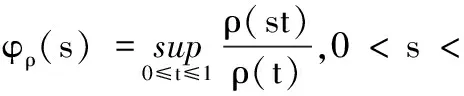
1 BMO-型特征

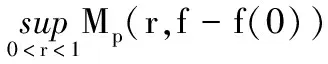

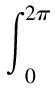
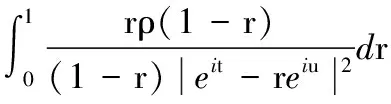

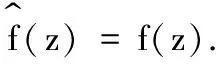





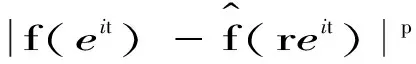
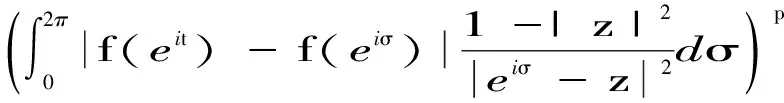


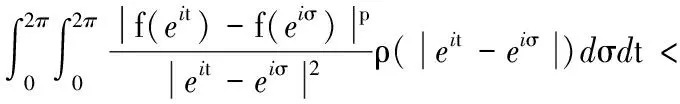
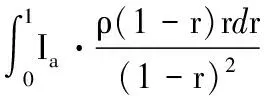
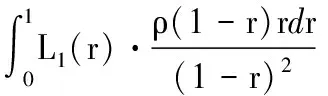





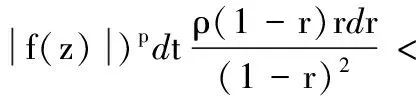
2 因式分解

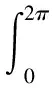
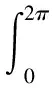
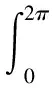
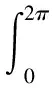
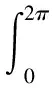

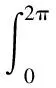
3 结论

