基于线性探测再散列的哈希表查找效率浅析

方瑞英　陈桂英

摘要：哈希表的理想情况是无需比较一次存取便能找到所查的记录，但是在实际应用中，哈希表通常存在冲突的情况，这就需要反复查找处理冲突。一般的搜索方法，在搜索时需进行关键字的比较。这一类建立在比较基础上的搜索方法，其效率依赖于搜索过程中所进行的比较次数。而通过使用哈希表人们可以不经任何比较，一次存取便能得到所需的信息，从而大大提高了搜索的效率。然而，建立哈希表不可能没有冲突，解决冲突则会产生诸如堆积、二次聚集等现象，降低了查找效率。文中通过举例阐明了线性探测再散列构造哈希表的方法，并详细地分析了查找成功时和查找失败时的ASL。

关键词：线性探测再散列；哈希表；ASL

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2015）015-0152-02

Abstract： The ideal condition of the hash table is to find the record without comparing an access. But in practice， the hash table usually has a conflict situation and needs to repeatedly look for conflict. General search methods need to carry out the comparison of key words. The efficiency of the search method based on the comparison of this class depends on the number of times in the search process. But by using a hash table， people can get the required information without any comparison and greatly improve the efficiency of the search. However， building a hash table cannot be without conflict. To resolve conflicts， such as the accumulation of two times， and other phenomena， reduces the search efficiency. In this paper， the method of constructing a hash table of the linear detection and hash table is illustrated by an example and the efficiency of the success and the failure is analyzed in detail.

Key words： Linear detection to hash；Hash Table； ASL

哈希表作为一种根据关键字直接进行访问的数据结构被广泛应用于各种查找中[1]。然而，很难找到一个哈希函数能保证对任意不同的关键字都产生不同的哈希值。通常用的处理冲突的方法有： 链地址法，开放定址法，再哈希法，以及建立一个公共溢出区。本文讨论基于线性探测再散列法如何构造哈希表及其查找效率的分析。在哈希表中，哈希函数的设置是非常灵活的，只要能使任一关键字由此所得的哈希地址都分布在哈希表允许的范围内就可以了。因此常常会出现不同的关键字值对应到同一个存储地址的现象，这就叫冲突。即关键字key1≠key2，但H（key1）= H（key2）。适当的选择分布均匀的哈希函数能有效地减少冲突的发生，但是不能不免冲突。发生冲突后，必须解决，也即必须寻找下一个可用的地址。因此哈希表的建立通常为如下步骤：第一步，取出一个数据元素的关键字key，根据哈希函数计算其在哈希表中的存储地址add，若地址为add 的存储空间还没有被占用，则将该数据元素存入，否则发生冲突，执行下一步；第二步，根据规定的冲突处理方法，计算关键字为key 的数据元素的下一个存储地址，若该地址的存储空间没有被占用，则存入，否则继续执行第二步，直到找出一个空闲的存储空间为止。由此可见，如何处理冲突是哈希表不可缺少的部分。

1 线性探测再散列法构造哈希表

开放定址法基本思想：当关键码key的哈希地址H0 = H（key）出现冲突时，以H0为基础，产生另一个哈希地址H1，如果H1仍然冲突，再以H0 为基础，产生另一个哈希地址H2，…，直到找出一个不冲突的哈希地址Hi，将相应元素存入其中。这种方法有一个通用的再散列函数形式： Hi=（ H（key）+di） mod m，i=1，2，…，m-1 ，其中H （key） 哈希函数，m为表长，di称为增量序列。增量序列的取值方式不同，相应的再散列方式也不同。主要有四种：线性探测再散列、二次探测再散列、伪随机探测再散列和双散列法。如果di增量序列取i时，称线性探测再散列。

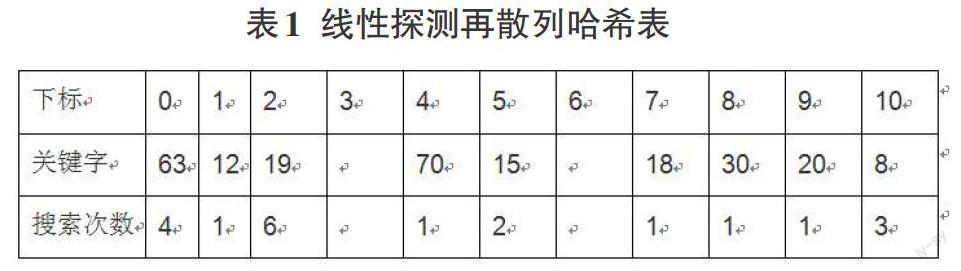
例如，已知散列表的地址区间为0～10，散列函数为H（k）=k MOD 11，采用线性探测再散列法处理冲突，将关键字序列20，30，70，15，8，12，18，63，19依次存储到散列表中。比如12、70、18、30、20这五个关键字探测一次即可存入空闲单元，而关键字8探测三次存入空闲单元，最后可以得到如下哈希表，见表1。

散列地址不同的结点争夺同一个后继散列地址的现象称为堆积（Clustering）。比如63和19，63 本来位置是8，直到探测了4次才找到合适位置0，19本来位置也是8，直到探测了6次才找到合适位置2。这将造成不是同义词的结点也处在同一个探测序列中，从而增加了探测序列长度，即增加了查找时间。 若散列函数不好、或装填因子a 过大，都会使堆积现象加剧。

2 线性探测再散列法查找效率分析

在哈希表上进行查找的过程和哈希造表的过程基本一致。给定K值，根据造表时设定的哈希函数求得哈希地址，若表中此位置上没有记录，则查找失败；否则比较关键字，若和给定值相等，则查找成功；否则根据造表时设定的处理冲突的方法找“下一个地址”，直至哈希表中某个位置为“空”或者表中所填记录的关键字等于给定值时为止。

查找成功的ASL指查找到哈希表中已有元素的平均探测次数，它是找到表中各个已有元素的探测次数的平均值。比如，给定值key=63的查找过程为：首先求得哈希地址H（63）=8，因为H.elem[8]不空且H.elem[8].key≠63，则找到第一次冲突处理后的地址H1=（8+1） MOD 11=9，而H.elem[9]不空且H.elem[9].key≠63，则找第二次冲突处理后的地址H2=（8+2） MOD 11=10， 而H.elem[10]不空且H.elem[10].key≠63，则找第三次冲突处理后的地址H3=（8+3） MOD 11=0， 而H.elem[0]不空且H.elem[0].key=63，则查找成功，查找次数等于构造哈希表时探测次数4。依此类推，可得等概率情况下查找成功的ASL为：

接下来讨论失败的情况， 查找失败的ASL是指在表中查找不到待查的元素，但找到插入位置的平均探测次数，它是表中所有可能散列的位置上要插入新元素时为找到空位置的探测次数的平均值。

计算失败时n是散列函数能够计算出的散列地址数，例如，若m=16，使用除留余数法，散列函数可以是H（x）=x%13，除数取不大于m但接近m的质数，此时n=13而不是16，sj是一旦在第j位置插入新元素（表中原来没有），要找到空闲位置的探测次数，也是它若存放进去，将来找到它的比较次数。也就是说，计算查找失败的次数就直接找关键字到第一个地址上关键字为空的距离即可， 但根据哈希函数，因此初始只可能在0～6的位置。等概率情况下，查找0～6位置查找失败的查找次数为：看地址0，到第一个关键字为空的地址3的距离为4，因此查找失败的次数为4；地址1， 到第一个关键字为空的地址3的距离为3，因此查找失败的次数为3；地址2， 到第一个关键字为空的地址3的距离为2，因此查找失败的次数为2；地址3，到第一个关键字为空的地址3的距离为1，因此查找失败的次数为1；地址4，到第一个关键字为空的地址6的距离为3，因此查找失败的次数为3；地址5，到第一个关键字为空的地址6的距离为2，因此查找失败的次数为2；地址6，到第一个关键字为空的地址6的距离为1，因此查找失败的次数为1；地址7，到第一个关键字为空的地址3（因为初始只可能在0～10之间，因此循环回去）的距离为8，因此查找失败的次数为8，依此类推，因此查找失败的ASL为：

3 结束语

线性探测法的优点：只要哈希表未被填满，总能找到一个空地址单元存放有冲突的元素；线性探测法的缺点：可能使第i个哈希地址的同义词存入第i+1个哈希地址，这样本应存入第i+1个哈希地址的元素变成了第i+2个哈希地址的同义词……因此，可能出现很多元素在相邻的哈希地址上“堆积”起来，大大降低了查找效率。解决方案：可采用二次探测法或伪随机探测法，以改善“堆积”问题。

参考文献：

[1] 严蔚敏，吴伟民.数据结构（C语言版）[M].北京：清华大学出版社，1998.

[2] 张朝霞，刘耀军.有效的哈希冲突解决办法[J]. 计算机应用， 2010（11）.

[3]王秋芬，邵艳玲. 一种新的基于哈希函数的排序算法[J].计算机与现代化，2010，9（10）.

[4]马如林，蒋华，张庆霞.一种哈希表快速查找的改进方法[J]. 计算机工程与科学， 2008（9）.

[5] 叶军伟.哈希表冲突处理方法浅析[J]. 科技视界， 2014（06）.

[6] 赵宇. 基于哈希表查找方法的优势及其算法的改进[J]. 中小企业管理与科技（下旬刊）， 2012（3）.

[7] 阮群生，李豫颖，刘锡铃.基于哈希表与线性表建立FP-Tree的改进算法[J]. 长江大学学报（自然科学版）理工卷， 2010（1）.

[8] 徐士良.实用数据结构[M].北京：清华大学出版社，2006.