基于改进量子蚁群算法的TSP求解问题研究

王启明，李玮瑶

（平顶山学院计算机科学与技术学院，平顶山467000）

基于改进量子蚁群算法的TSP求解问题研究

王启明，李玮瑶

（平顶山学院计算机科学与技术学院，平顶山467000）

TSP问题是一个组合优化问题，该问题具有NP计算复杂性，运用量子蚁群算法求解该问题时易陷入局部最优和收敛速度慢的问题。因此提出一种基于博弈论的量子蚁群算法（GQACA），该算法采用重复博弈模型，在重复博弈中产生一个博弈序列，使得每次博弈都能够产生最大效益，并得到相应博弈过程的纳什均衡。把该算法应用于TSP求解，实验结果表明本文中GQACA算法的收敛精度和稳定性均要优于其他量子蚁群算法。

改进；博弈论；蚁群算法；旅行商问题

1 引 言

旅行商问题，即TSP问题（Travelling Salesman Problem），又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一［1-2］。可以描述为：已知n个城市之间的相互距离，现有一推销员必须遍访这n个城市，并且每个城市只能访问一次，最后又必须返回出发的城市。如何安排他对这些城市的访问次序，可使其旅行路线的总长度最短？解决旅行商问题的各种优化算法，都是通过牺牲解的精确性来换取较少的耗时［3］。其他一些启发式的搜索算法则依赖于特定的问题域，缺乏通用性。相比较而言，遗传算法是一种通用性很好的全局搜索算法，因此遗传算法是解决旅行商问题的一种不错的算法。贾瑞玉等分析了量子蚁群算法的优缺点，提出一种新的求解旅行商问题（Traveling Salesman Problem，TSP）的混合量子蚁群算法［4-5］。博弈论的最大特点是能够为相应的博弈过程找到纳什均衡点，而纳什均衡点也正是策略的最优点［6］。该算法设计扩大解的搜索空间，改善种群信息结构，避免搜索陷入局部最优。并将该算法与目前比较常用的一些算法进行了比较，结果表明该算法具有更好的收敛速度［7-8］。

2 博弈论概念简介

博弈论是研究决策主体在给定信息结构下如何决策以最大化自己的效用［8］。博弈由3个基本要素组成，即局中人、策略集、效用。一般的，非合作策略式博弈由三种要素组成：博弈的参与者集合，i∈N，N＝1，2，...，n；参与者的策略空间，pi，i＝1，2，...，n；每个参与者的支付函数，ui（p1，p2，...，pn），i＝1，2，...，n。博弈的策略可以表述为：

纳什均衡是指在某一策略组合中，所有的参与者面临这样一种情况，当其他人不改变策略时，他此时的策略是最优的。即在策略式博弈G＝｛p1，p2，...，pn；u1，u2，...，un｝中，如果对任何其他参与人的策略组合p－i，参与人i的策略是严格最优选择，即：

由以上理论，进行如下定义：

εi被称为参与者i的占优策略。这里公式（3）中的εi（p－i）＝εi（p）。定义E（p）＝［εi（p－1），εi（p－2），...，εn（p－n）］T为整个博弈的最优策略集合。最优策略集合与纳什均衡是一致的。所以策略E（p）是一个纯策略纳什均衡。此时对每个参与者都满足：

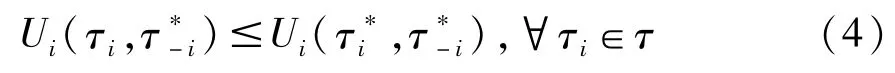
每一个理性的参与者都不会有单独改变策略的冲动。

3 基于博弈论的量子编码蚁群算法（GQACA）

3.1 非合作博弈模型

为不失一般性，本文以求函数的最小值为例，下式始终成立。

其中t为迭代次数，F为最优值函数。非合作博弈理论中，参与者只根据他们可察觉的自我利益（perceived self-interest）来决策。参与者之间的威胁、协议、许诺之类，是无法实施的，即便参与者在博弈中可以相互沟通。除了那些博弈规则确实允许的协议外，参与者无法达成有约束力的协议。对于一个两只蚂蚁博弈模型而言，分别用“1”和“2”代替两个博弈方，当“1”首先进行策略选择时，它会选择使自己的收益尽可能大的策略，然后“2”可根据自身收益来考虑是接受还是拒绝由“1”提出的策略，如果“2”不受益，就不接受，如果“2”受益，就接受，并且自动获得下一轮的优先选择权。

3.2 初始种群产生

在GQACA中，采用如下编码方案

其中θij＝2π×rnd；（i，j＝1，2，...，m），m是种群规模，n是空间维数，rnd为（0，1）之间的随机数，这两个位置分别对应量子态｜0＞和｜1＞的概率幅。

qi0为｜0＞态位置，qi1为｜1＞态位置。

3.3 蚂蚁位置变异处理

基于博弈模型的改进算法使用一种通过量子非门设计的变异操作，具体步骤如下：

（1）以概率Qm从量子蚂蚁种群中选取若干个个体；

（2）对选中的量子蚂蚁个体按概率Pm确定一个或多个变异位；

（3）对选中位量子比特的几率执行量子非门操作。

3.4 最优位置更新规则

设蚂蚁Pi当前搜索到的最优位置为：

整个种群目前搜索到的最优位置为：

位置状态更新规则描述为：

（1）蚂蚁Pi上量子位角增量的更新

其中

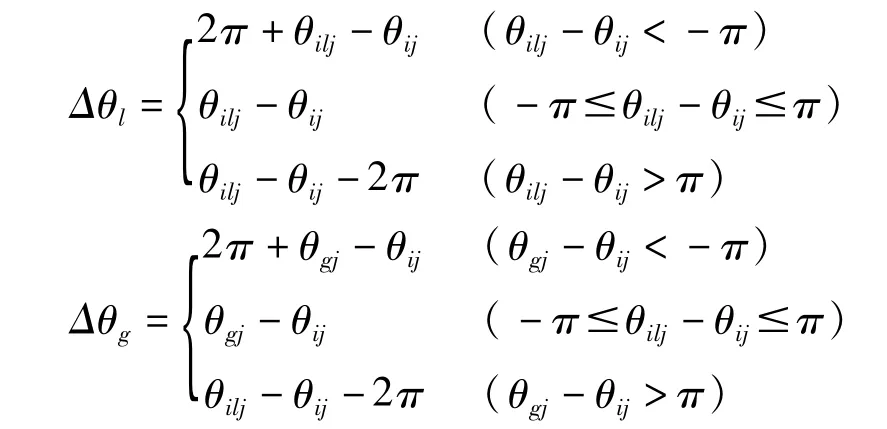
（2）蚂蚁Pi上量子位概率幅的更新

蚂蚁Pi更新后的两个新位置为：

4 仿真实验结果与分析

为验证本文算法的有效性以及可行性，本文利用3个典型的标准测试函数对GQACA算法寻优性能进行测试。应用于TSP问题求解；测试函数（15）主要测试算法陷入局部最优的问题。实验采用测试函数（16）Rosenbroc函数以及测试函数（17）Bohachevsky函数进行优化［9-11］，寻找函数极值来测试算法在时间上的优越性。

测试函数（15）

其中x∈［－500，500］；

测试函数（16）Rosenbroc函数：

其中（－2.048≤xi≤2.048，i＝1，2）

测试函数（17）Bohachevsky函数：首先对测试函数进行测试，将GQACA测试结果与QACA和基准的ACA的结果进行比较。得到三种比较结果如表1所示。

表1 三种算法优化结果比较Tab.1 Optimization results of three algorithms

5 结束语

主要从解决TSP问题的收敛精度和稳定性角度出发，分别介绍了博弈论的概念和基于博弈论的量子蚁群算法的实现方法，并利用三个典型函数对GQACA算法进行性能测试。结果表明，该模型不仅能够模拟生物种群的自然进化，而且能够模拟生物种群进化过程中的文化进化，从而体现文化进化对自然进化的指导作用及其加速自然进化的重要意义，算法的收敛精度和稳定性均要优于其他算法。

［1］ Colorni A，Dorigo M，Maniezzo V.Distributed optimization byant colonies［C］.Proceedings of 1st European Conference of Ar-tificial Life.Paris：Elsevier Publisher，1991：134-142.

［2］ Dorigo M.Optimization，learning and nature algorithms［D］.Italy：Politecnico diMilano，1992.

［3］ P C Li，H Y Wang，Quantum Ant Colony Optimization Algorithm Based on Bloch Spherical Search［J］.Neural Network World，2012，22（4）：325-341.

［4］ P Li，K Song，E Yang.Quantum ant colony optimization with application［J］.2010 Sixth International Conference on Natural Computation（ICNC），2010：2989-2993.

［5］ W Honggang，M Liang，Z Huizhen，et al.Quantuminspired ant algorithm for knapsack problems［J］.Journal of Systems Engineering and Electronics，2009，20（5）：1012-1016.

［6］ Chandra Mohan B，Baskaran R.A survey：Ant Colony Optimization based recent research and implementation on several engineering domain［J］.Expert Systems with Applications，2012，39（4）：4618-4627.

［7］ Dorigo M，Gambardella LM.Ant colonies for the traveling sales-man problem［J］.BioSystems，1997，43：73-81.

［8］ Stützle T，Hoos H H.Max-min ant system［J］.Future GenerationComputer Systems，2000，16（8）：889-914.

［9］ 刘玉岭，冯登国，吴丽辉，等.基于静态贝叶斯博弈的蠕虫攻防策略绩效评估［J］.软件学报，2012，23（3）：712-723.

Liu Yuling，Feng Dengguo，Wu Lihui，et al.Bayesian game based on static performance evaluation worm attack and defense strategies［J］.Journal of Software，2012，23（3）：712-723.

［10］ 朱建明，Srinivasan Raghunathan.基于博弈论的信息安全技术评价模型［J］.计算机学报，2009，32（4）：828-834.

Zhu Jianming，Srinivasan Raghunathan.Information security technology evaluationmodel based on game theory［J］.Journal of Computers，2009，32（4）：828-834.

［11］ 高尚.解决旅行商问题的混沌蚁群算法［J］.系统工程理论与实践，2005，25（9）：100-104.

GAO Shang.Solving Traveling Salesman Problem by Chaos Ant Colony Optimization Algorithm［J］.Systems Engineering-theory＆Practice，2005，25（9）：100-104.

Study of TSP Problem Solving Based on Im proved Quantum Ant Colony Algorithm

Wang Qiming，LiWeiyao
（School of Computer Science and Technology，Pingdingshan University，Pingdingshan 467002，China）

TST，as a combinatorial optimization problem，is solved by Quantum ant colony algorithm which is easy to fall into the local optimum and slow convergence.The quantum ant colony algorithm，based on game theory（GQACA），is put forward in this paper.It uses the repeated game to create the repeated game sequence formaximum benefit in each game，and get the corresponding game process of Nash equilibrium.The typical test functions are used for GQACA algorithm optimization performance experiment testing.The experimental results show that the GQACA convergence precision and stability of the algorithm are better than QACA algorithm and ACA one.

Improved；Game theory；Ant colony optimization；Travelling Salesman Problem

10.3969/j.issn.1002-2279.2015.03.010

TN393

A

1002-2279（2015）03-0031-03

王启明（1980-），男，河南鲁山人，硕士研究生，讲师，主研方向：软件工程算法和物联网。

2014-11-18