大口径反射面天线PFDTD-PTDPO混合模拟时的网格剖分要求

朱湘琴，王建国，2，邢笑月

（1.西北核技术研究所，西安710024；2.西安交通大学电子与信息工程学院，西安710049）

大口径反射面天线PFDTD-PTDPO混合模拟时的网格剖分要求

朱湘琴1，王建国1，2，邢笑月1

（1.西北核技术研究所，西安710024；2.西安交通大学电子与信息工程学院，西安710049）

采用并行时域有限差分（PFDTD）和并行时域物理光学（PTDPO）相混合的方法对大口径反射面天线近轴区的辐射远场进行了模拟计算。以圆锥喇叭馈电的单反射面天线为例，给出了馈源及反射面网格剖分的要求；根据此要求剖分网格，给出了卡塞格伦双反射面天线的时域算例，所得计算结果与CST软件的计算结果符合较好。该网格剖分要求可用于PFDTDPTDPO混合方法中进行任意馈源馈电的大型反射面天线的瞬态模拟，包括馈源偏焦的情况。

时域；反射面天线；并行时域有限差分；并行时域物理光学；网格剖分；近轴区；远场

反射面天线已广泛应用于通信、雷达和射电天文中。对大型反射面天线进行分析和设计时，常采用纯高频近似分析法［1 6］或商用软件，如FEKO软件［7］，但频域方法每次计算只能得到一个频率点的信息，无法给出某个频段内的时域特性，且对反射面天线具有复杂馈源的情形，求解比较困难。考虑到反射面天线往往是电大尺寸（其口径面可达数十或数百个波长），而馈源和馈电结构的尺寸往往与波长同量级，故文献［8- 10］均使用并行时域有限差分方法（PFDTD）计算馈源的近场，再借助基尔霍夫表面积分表达式［11］（KSIR）和并行时域物理光学方法（PTDPO）求得反射面天线辐射远场的瞬态辐射响应。

无论是双反射面天线还是单反射面天线，使用PFDTD-PTDPO模拟计算时均涉及源和反射面照明区的网格剖分。其中，源被剖分为长方体或立方体的网格（FDTD网格），反射面照明区被剖分为三角形网格。但文献［8- 10］均未给出源的FDTD网格及反射面上三角形网格的剖分标准。因此，本文以圆锥喇叭馈电的单反射面天线为例，给出了不同尺寸的FDTD网格和三角形网格的计算结果，总结了PFDTD-PTDPO混合方法计算时的网格剖分要求，并将该要求应用于大型双反射面天线的瞬态响应模拟中。

1 方法简介

使用PFDTD-PTDPO混合方法［8 10］计算反射面天线的远区瞬态辐射场。模拟单反射面天线远区辐射场的计算思路如下：1）使用PFDTD方法计算包含馈源的近场，同时，通过KSIR求得反射面照明区三角形面网格上的瞬态磁场；2）借助PTDPO方法，由反射面照明区上的瞬态磁场外推得到单反射面天线远区辐射场的瞬时值。模拟双反射面天线远区瞬态辐射场的计算思路如下：1）使用PFDTD方法计算包含馈源的近场，同时，通过KSIR求得次反射面照明区及其附近3个面上的瞬态磁场；2）借助KSIR，由上述3个面上的瞬态磁场求得主反射面照明区三角形面网格上的瞬态磁场；3）借助PTDPO方法，由主反射面照明区上的瞬态磁场外推得到主反射面天线远区辐射场的瞬时值。

下面以单反射面天线为例，给出KSIR的计算公式。图1给出了KSIR计算反射面上任意点Q磁场的示意图。

设单反射面天线上位置矢为R′的Q点在t′时刻的磁场为hinc（R′，t′），则根据KSIR的具体形式［11］，该磁场可表示为

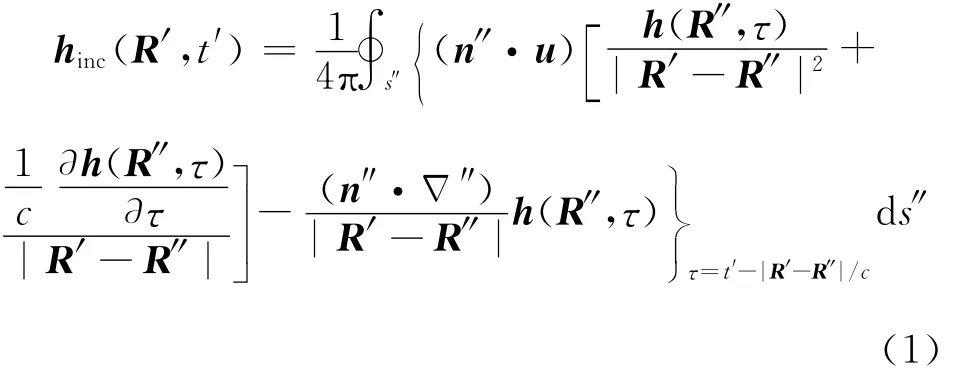
式中，R′对应反射面照明区上剖分出的三角形面网格重心点Q的位置；t′＝τ＋｜R′－R″｜／c；R″为s″面（Kirchhoff surface，KS）上任意一点的位置矢量（如图1所示）；n″为s″面上该任意点的法向单位矢量；｜R′－R″｜为s″面上该任意点与反射面上Q点的距离；u＝（R′－R″）／｜R′－R″｜；h（R″，τ）为τ时刻s″面上该任意点的磁场；Δ″是对磁场求梯度的拉普拉斯算符。式（1）中，n″·u及n″·Δ″由组成KS的6个面决定。

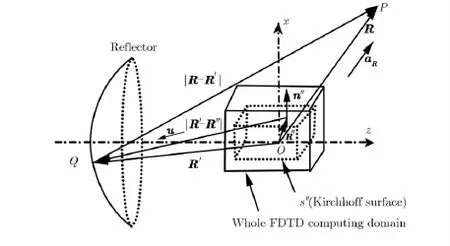
图1使用KSIR计算反射面上Q点磁场的示意图Fig.1 Schematic of geometric relation for computing magnetic field at point Q on reflector using KSIR

2 仿真模拟及结果分析

当激励源为短脉冲时，源包含的是一段频谱的信息，故计算结果也会包含一段频谱的信息。通常，网格剖分的要求一般由频谱的上限频率所确定。因此，可假设已知一段频谱的上限频率，并将该频率设置为所关心的频率，以该频率的正弦波作为激励源，使用PFDTD-PTDPO混合方法来分析不同网格尺寸时，单反射面天线近轴区若干测试点远区瞬态响应的变化，从而给出反射面天线系统计算时，源及反射面网格尺寸剖分的要求。

2.1 正弦波激励的圆锥喇叭馈电的单反射面天线的模拟分析

设抛物面天线的口径D＝562.5 mm，F／D＝0.4，F为抛物面的焦距；抛物面的馈源为圆锥喇叭，且圆锥喇叭馈源的中点与抛物面的焦点重合。圆锥喇叭中波导的半径为0.015 5 m，波导长度为0.094 m；喇叭天线的口径为0.077 m，喇叭长度为0.094 m。采用PFDTD-PTDPO混合方法模拟前，将圆锥喇叭馈源划分成立方体，其FDTD网格尺寸δ＝1 mm。取FDTD时间步长Δt＝δ／（2c）。波导的末端口有8层CPML截断边界。喇叭中波导激励源为TE11模式固定频率的正弦波。使用NetGen库函数将反射面天线的照明区划分成贴近反射面的三角形面网格。

表1给出了当源的FDTD网格尺寸固定为1 mm时所关心的频率f、波长λ、FDTD模拟时的最大网格尺寸δmax＝λ／10及其他相关参数。表2给出了反射面上剖分的三角形网格总数M2＿max、三角形单元的最小尺寸δr及其相关参数。下面分别对表1所列的4个频率进行模拟分析，以说明源的网格剖分、单反射面照明区的网格剖分对单反射面天线远区辐射场的影响。

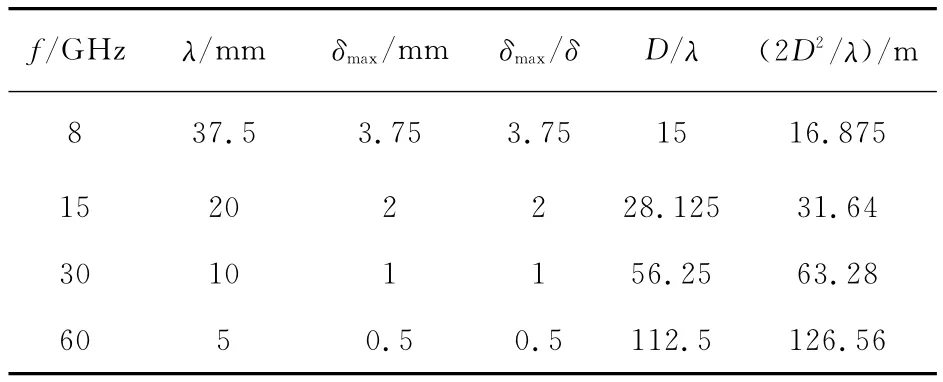
表1 各频率对应的波长及相关参数Tab.1 Corresponding wavelengths to each frequency and its related parameters

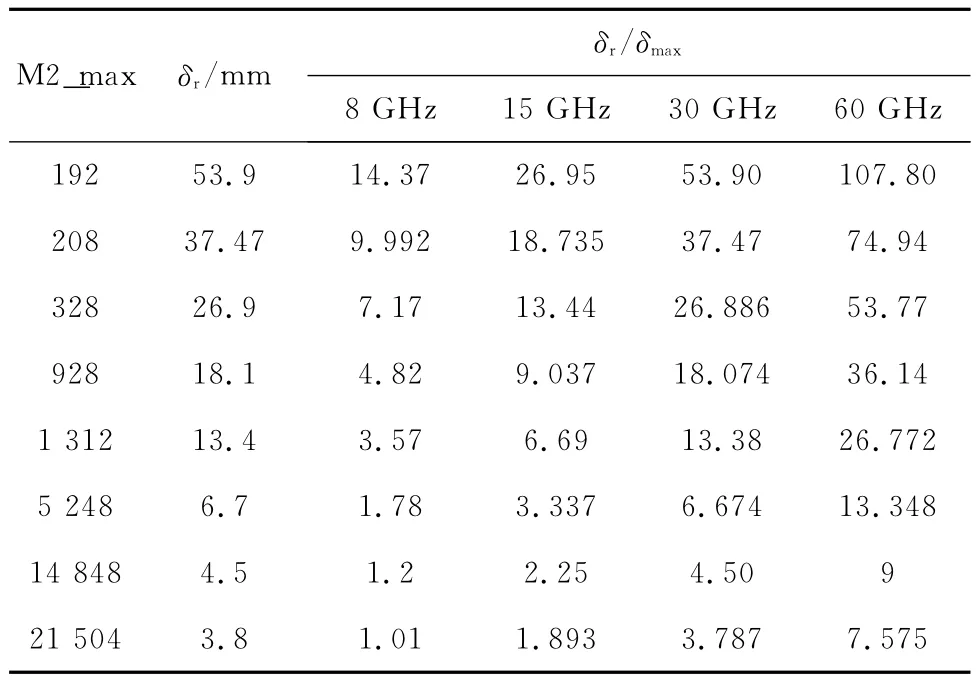
表2 反射面上三角形网格总数及其对应的最小尺寸和其他相关参数Tab.2 Corresponding minimum sizes to each triangle division on reflector and its related parameters

图2给出了f＝8 GHz、单反射面天线上网格剖分数目不同时，R＝2D2／λ处主轴及偏离主轴1°的接收点处场强的瞬态值。由图2可知，当源的网格尺寸δ＝1 mm（即δmax／δ＝3.75）、反射面上δr／δmax分别为1.01，7.17，9.992，14.37时，同一个接收点处场强的计算结果基本相同；且取δr／δmax＝14.37与δr／δmax＝1.01时，R＝2D2／λ处同一个测试点场强幅值相差约4.0%。在本例中，由于对反射面进行三角形网格剖分时，δr／δmax＝1.01和δr／δmax＝7.17时的计算结果基本一致，因此，下面对单反射面天线的模拟分析中，可取三角形网格剖分后δr／δmax介于1.01～7.17之间的计算结果作为标准进行比较。

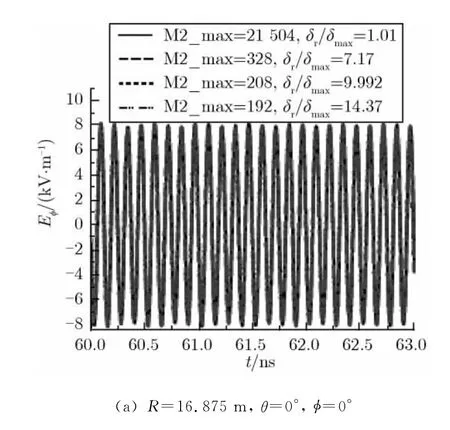
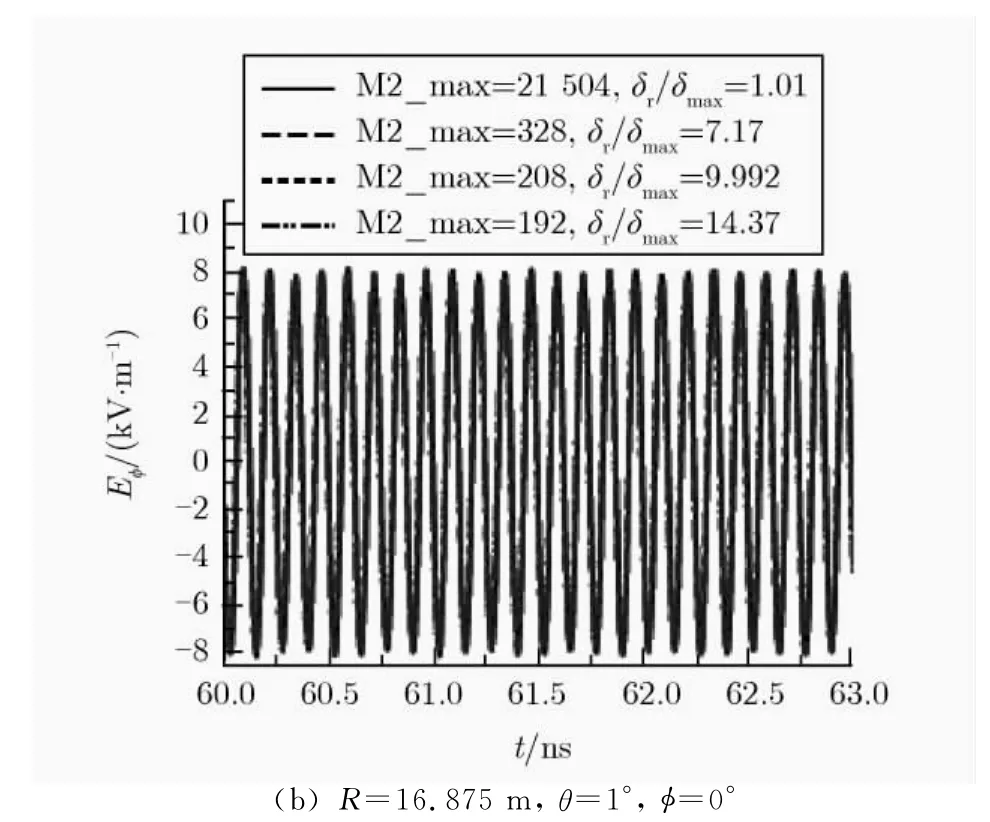
图2 单反射面剖分的三角形网格数目不同时，R＝2D2／λ处的场强（f＝8 GHz）Fig.2 Far-fields at R＝2D2／λwith different sizes of triangles on a single reflector（f＝8 GHz）

图3给出了f＝15 GHz、单反射面天线上网格剖分数目不同时，R＝2D2／λ处的2个测试点的场强。由图3可知，当f＝15 GHz时，δmax／δ＝2，δr／δmax分别为3.337，9.037，18.735时，同一个测试点的场强计算结果基本相同。其中，δr／δmax分别为3.337，9.037时，R＝2D2／λ处主轴上场强的幅值基本相同；δr／δmax分别为18.735，3.337时，R＝2D2／λ处同一个测试点场强幅值最大相差约8.1%。此外，根据表2可知，f＝15 GHz时，δr／δmax＝18.735对应的网格数为208，而f＝8 GHz时，δr／δmax＝9.992对应的网格数也为208。但后者的计算结果与反射面上细网格的情形符合得更好，说明关心的频率越高，反射面上三角形网格就需要划分得越密。

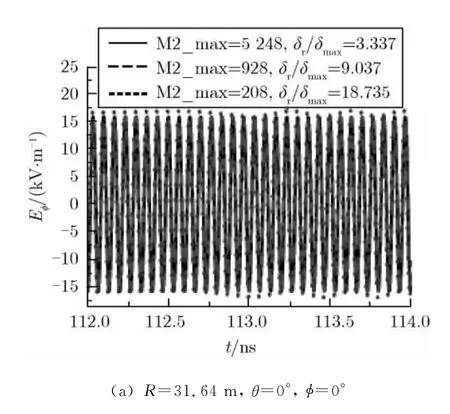
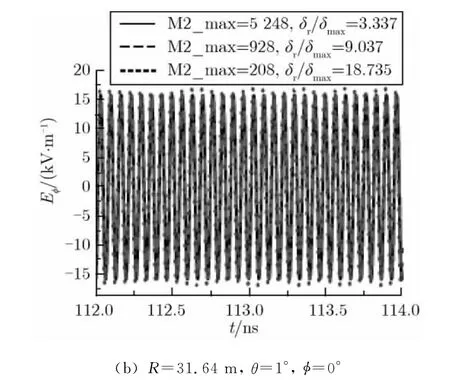
图3 单反射面剖分的三角形网格数目不同时，R＝2D2／λ处的场强（f＝15 GHz）Fig.3 Far-fields at R＝2D2／λwith different sizes of triangles on a single reflector（f＝15 GHz）

图4给出了f＝30 GHz、单反射面天线上网格剖分数目不同时，R＝2D2／λ处的2个测试点的场强。由图4可知，当f＝30 GHz，δmax／δ＝1，δr／δmax分别为6.674，18.074，26.886时，同一个测试点的场强基本相同；δr／δmax分别为26.886，6.674时，同一个测试点场强相差约2.4%。此外，根据表2可知，f＝15 GHz时，δr／δmax＝18.735对应的网格数为208，而f＝30 GHz时，δr／δmax＝26.886对应的网格数为328。但后者的计算结果与反射面上细网格的情形符合得更好，说明无论关心的频率是高还是低，反射面上的网格数越多，其计算结果就越精确。且随着所关心频率的增高，作为三角形网格剖分要求的δr／δmax，其值可能呈增大的趋势。即，当δmax／δ≥1，且关心的频率f≥30 GHz时，若取δr／δmax≤26.886，应该能保证计算结果与细三角形网格的计算结果符合得很好。

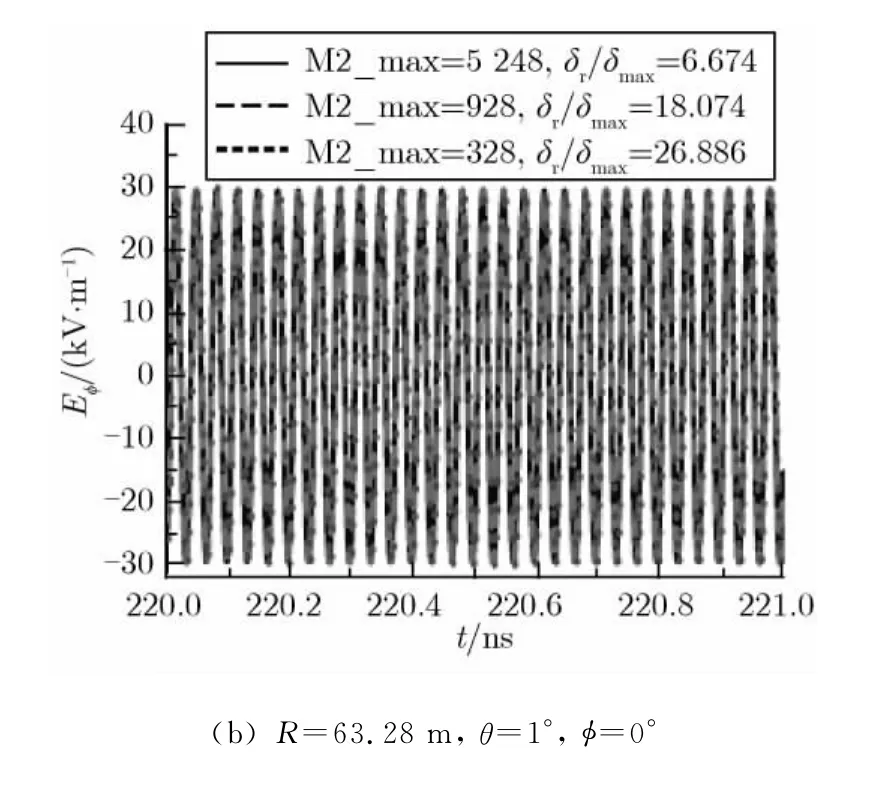
图4 单反射面剖分的三角形网格数目不同时，R＝2D2／λ处的场强（f＝30 GHz）Fig.4 Far-fields at R＝2D2／λwith different sizes of triangles on a single reflector（f＝30 GHz）

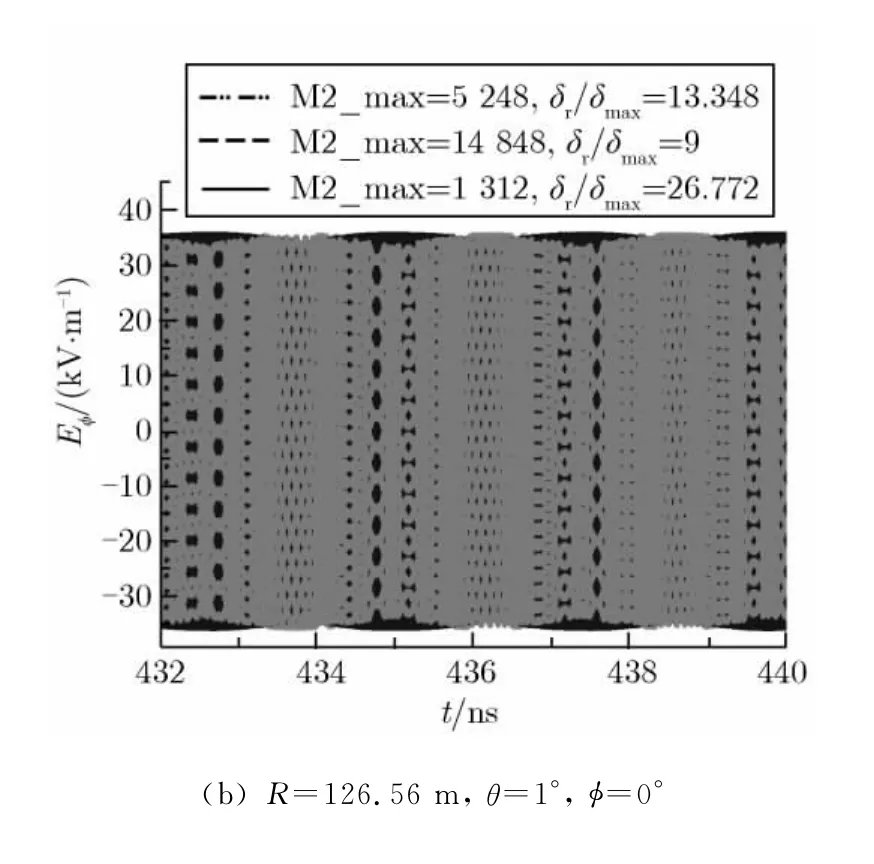
图5 单反射面剖分的三角形网格数目不同时，R＝2D2／λ处的场强（f＝60 GHz，δ＝1 mm）Fig.5 Far-fields at R＝2D2／λwith different sizes of triangles on a single reflector（f＝60 GHz，δ＝1 mm）

图5给出了f＝60 GHz，单反射面天线上网格剖分数目不同时，R＝2D2／λ处的2个测试点的场强。根据经验可知，当喇叭馈源由正弦或余弦激励时，单反射面天线主轴上的辐射场也应该按正弦或余弦的规律周期振荡，幅值应该比较稳定。由图5可见，当源的网格尺寸为1 mm（即δmax／δ＝0.5），δr／δmax分别为9，13.348和26.772时，同一个测试点的场强随时间周期振荡，但其幅值出现了明显的波动。说明计算结果并不准确。为此，需要将源的网格尺寸取小一点。

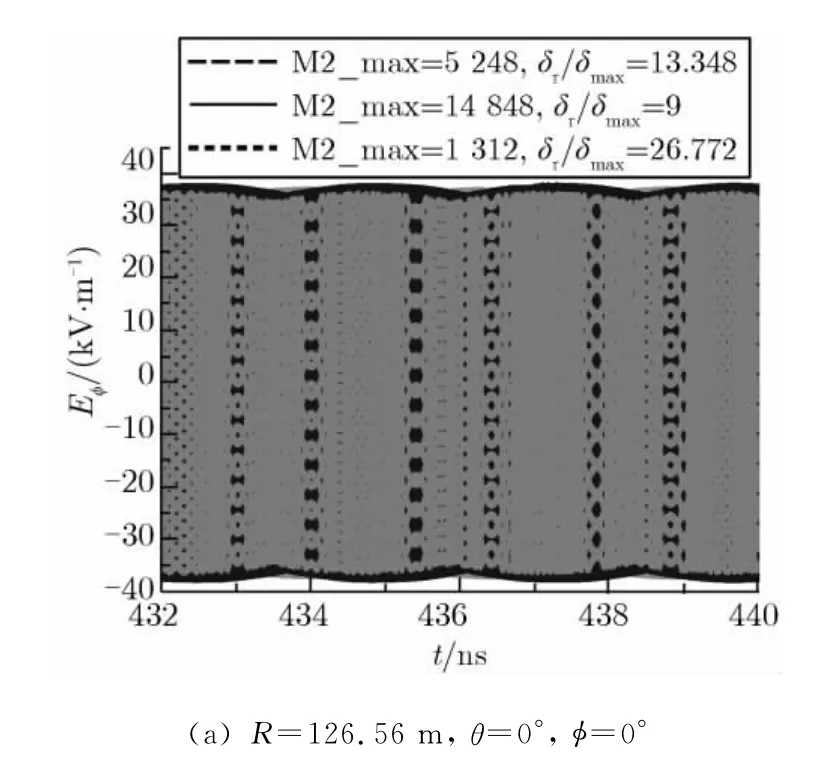
将源的网格尺寸取为0.5 mm（即δmax／δ＝1），图6给出了f＝60 GHz，单反射面天线上网格剖分数目不同时，R＝2D2／λ处的2个测试点的场强。由图6可知，当δmax／δ＝1，δr／δmax为9和26.772时，同一个测试点的场强基本相同，且场振荡幅度稳定。由此可知，对源的网格尺寸的选取，必须满足δmax／δ ≥1的条件。这与FDTD计算时网格尺寸剖分要求［12］一致。

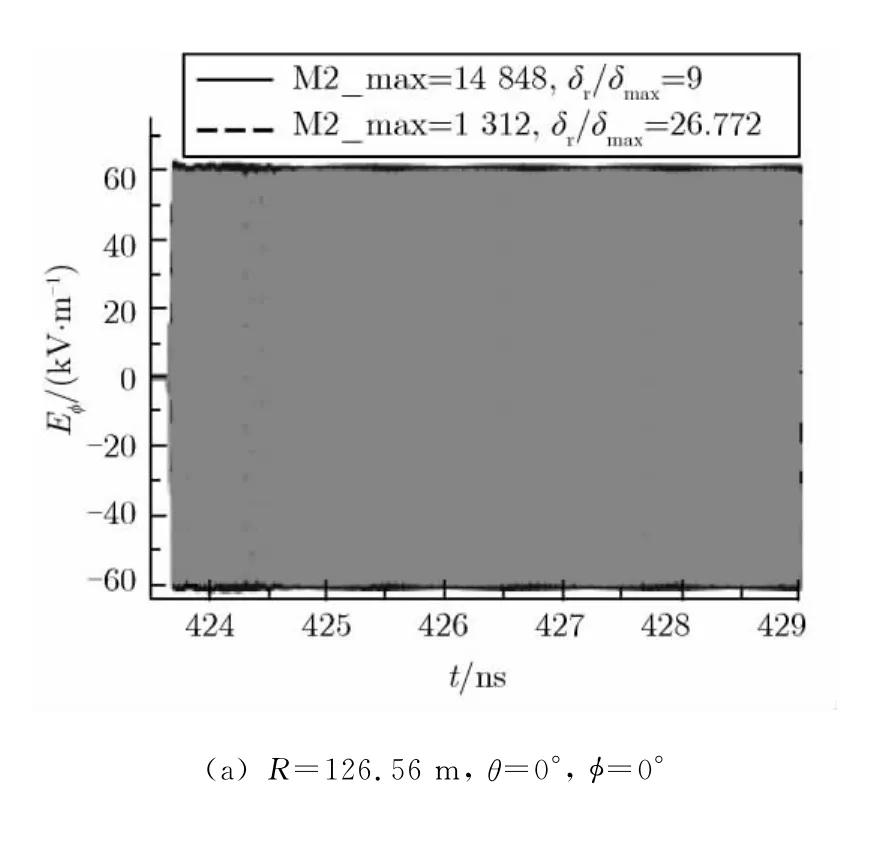
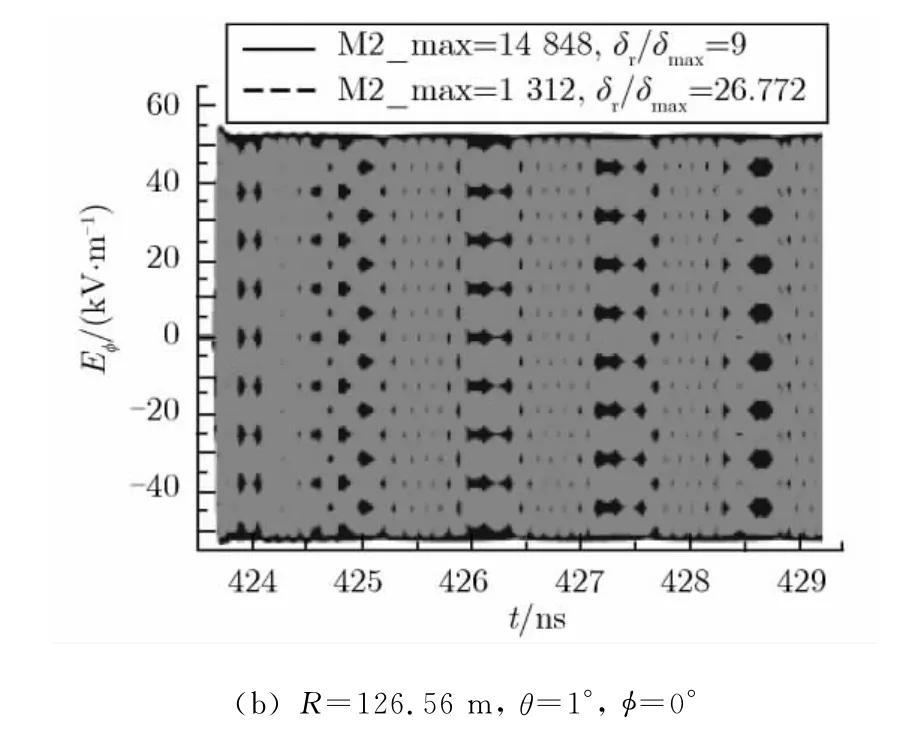
图6 单反射面剖分的三角形网格数目不同时，R＝2D2／λ处的场强（f＝60 GHz，δ＝0.5 mm）Fig.6 Far-fields at R＝2D2／λwith different sizes of triangles on a single reflector（f＝60 GHz，δ＝0.5 mm）

根据上面的分析，对单反射面天线系统中源和反射面的网格剖分可以给出如下结论：

1）源的网格尺寸将直接影响计算结果的准确性，必须满足δmax／δ≥1的条件。其中，δmax＝λ／10，λ为最高（或固定）频率点对应的波长；2）若关心的频率越高，则反射面上三角形网格需要划分得越密；3）当δmax／δ≥1，且关心的频率f≥30 GHz时，若反射面上三角形的δr／δmax≤26.886时，在R＝2D2／λ处的主轴及偏离主轴小角度的位置上，计算得到的场幅值与细三角形网格情形的对应值相差在10%以内；4）无论关心的频率是高还是低，反射面上的网格数越多，计算结果越精确，且随着频率的增高，要求的δr／δmax值可能呈增大的趋势。图7给出了本算例中δmax／δr≥1，反射面天线的辐射远场计算准确时，容许的δr／δmax最大值与频率的关系曲线。

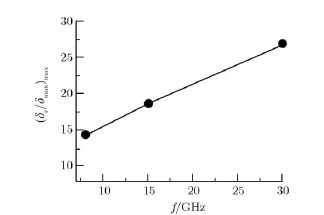
图7δr／δmax的最大值与频率的关系Fig.7 The maximum ofδr／δmaxvs.frequency

2.2 卡塞格伦双反射面天线算例

将上述单反射面天线系统网格剖分的规律应用于卡塞格伦双反射面天线系统的网格剖分中。图8给出了某卡塞格伦双反射面天线系统的示意图。该系统的激励源为载频f＝10 GHz的高功率微波脉冲，并设对应的角频率ω＝2πf，波长λ＝c／f＝0.03 m。设主反射面为抛物面，其口径D＝1 m（即D≈33.33λ），F／D＝0.3。次反射面为旋转双曲面；构成双曲面的双曲线的实轴长71.51 mm，虚轴长83.45 mm。主反射面和次反射面的焦点重合，并以该焦点为原点，建立xyz坐标系。双反射面天线的馈源为圆锥喇叭，圆锥喇叭中波导的半径为10.5 mm，波导长度为60 mm；喇叭天线的口径为81 mm，喇叭长度为86.25 mm。

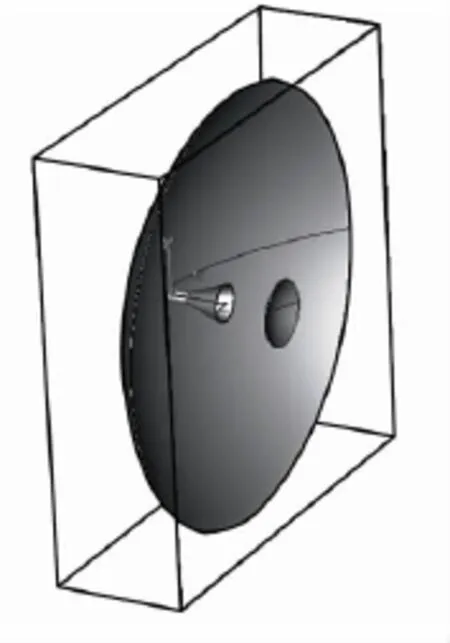
图8 卡塞格伦天线示意图Fig.8 Cassergrain antenna

激励源脉冲上升沿为5 ns，半高宽为10 ns，脉冲表达式为

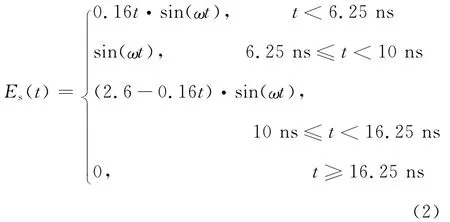
该脉冲的时域及频域波形如图9所示。由图9 （b）可知，以频域最大值的1／1 000为标准，该短脉冲的频率上限fmax≈11.07 GHz。此时，对应的δmax≈2.71 mm，即频率上限对应波长的1／10。

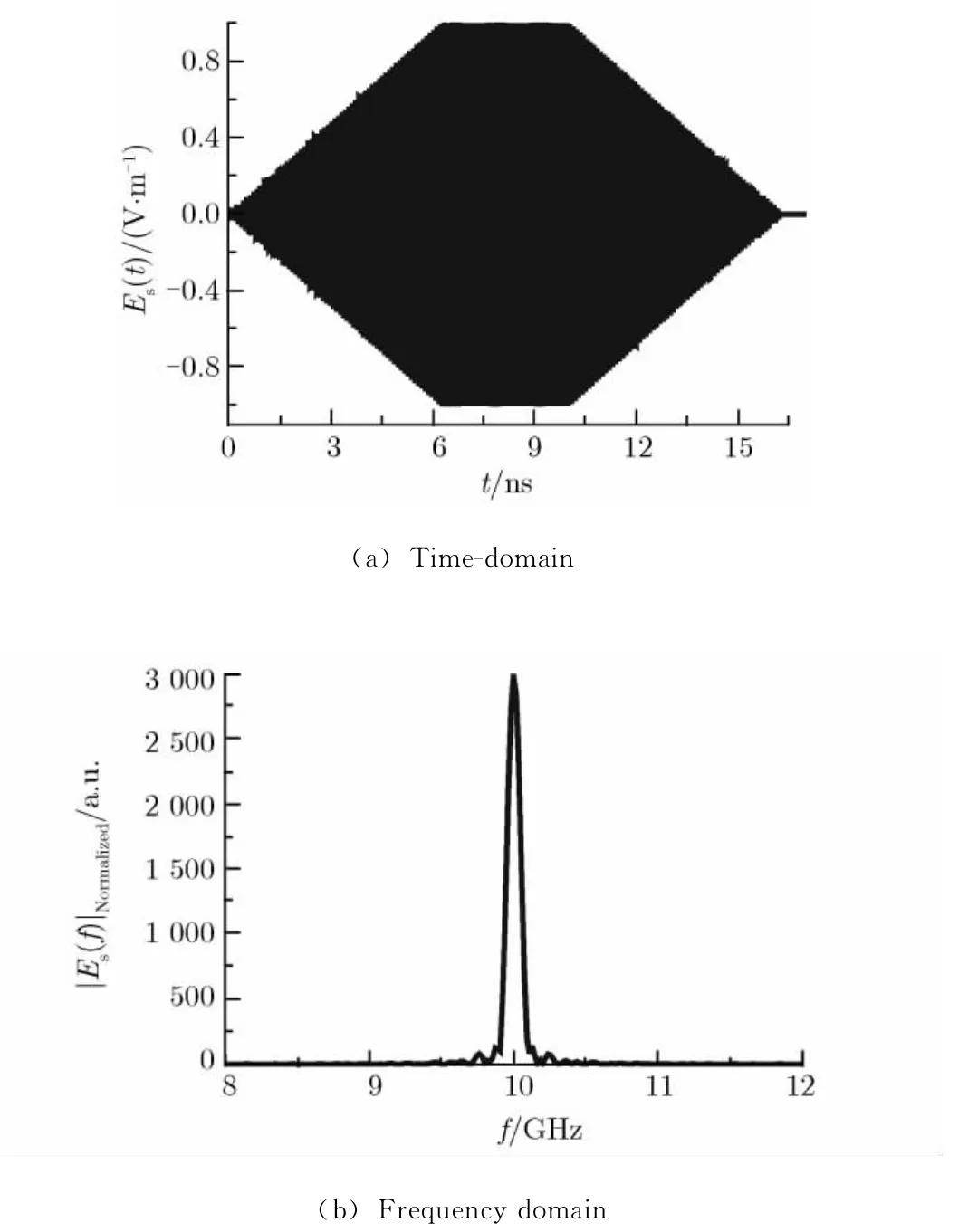
图9上升沿为5 ns，半高宽为10 ns的HPM短脉冲Fig.9 High power microwave short pulse with 5 ns rise-time and 10 ns half-width

PFDTD方法计算时可取网格尺寸为1 mm（满足δmax／δ≥1的条件）。将副反射面剖分为3 840个贴近副反射面的三角形面片，三角形网格的最小尺寸δr＝2.67 mm，此时δr／δmax≈0.985；将主反射面剖分为48 128个贴近反射面的三角形面片，三角形网格的最小尺寸为5.5 mm，此时δr／δmax≈2.03。对主次反射面网格的剖分均满足第2.1节中的三角形网格剖分要求（见图7）。根据PFDTD-PTDPO方法计算出该双反射面天线系统距离主反射面焦点R ＝79.7 m处几个接收点的瞬态响应如图10所示。

由图10可知：1）计算得到主轴及其附近3个小角度测试点场检波波形的上升沿均为5.03 ns，半高宽均为9.96 ns，说明主轴和主轴附近很小角度内场的上升沿和半高宽变化很小，这是由于主反射面照明区上所有点对主轴附近测试点的光程差基本一致的缘故；2）主轴上接收点的场强峰值约为4.63 V·m－1，而根据CST软件计算得到主轴上场强峰值为4.97 V·m－1，两者相差约6.8%。

图10卡塞格伦天线系统R＝79.7 m的近轴区几个测试点的场强Fig.10 Far-fields at R＝79.7 m with several received angles of Cassergrain antenna

表3给出了R＝79.7 m处偏离主轴小角度的5个测试点的场强幅值与主轴上场强幅值E的比值。作为比较，表中还给出了使用CST软件计算得到的相应结果。

由表3可知：偏离主轴2°以内，即在远场主瓣的6 d B（对应的幅值之比约为0.25）区以内的接收点，本文的计算结果与CST计算结果相比，符合较好；当偏离主轴角度比较大时，本文计算结果偏大。这是由于CST软件使用的是全波算法，即将源、次反射面和主反射面作为一个整体来进行考虑。而本文使用PTDPO方法计算反射面的远区辐射场时，忽略了反射面的边缘绕射，且不考虑源和次反射面对远场的二次贡献，因此，只在近轴区有效，由此可说明，当使用前文介绍的网格剖分要求来剖分反射面系统时，PFDTD-PTDPO混合方法可以准确模拟双反射面天线近轴区的远区瞬态辐射场。需要特别注意的是，CST软件无法应用于超大尺寸的双反射面天线的瞬态辐射模拟。

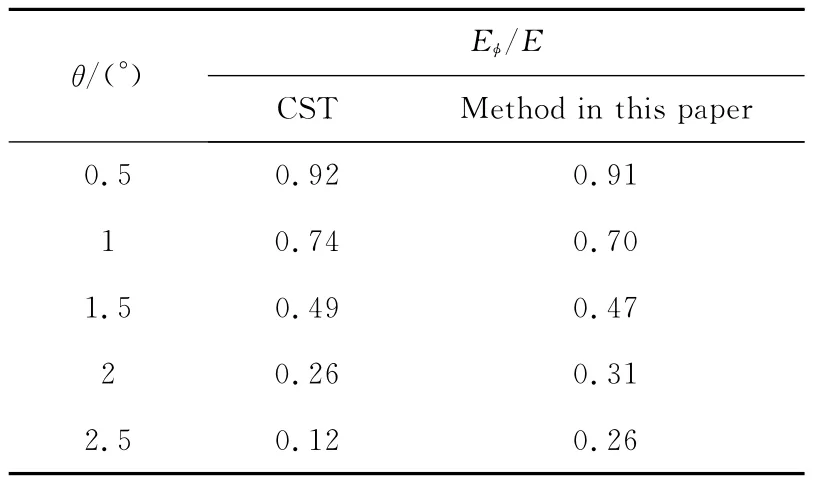
表3 偏离主轴的场强幅值与主轴上场强幅值之比Tab.3 Ratios of the electric-field’s amplitude at several received angles to that at the main axis

3结论

采用PFDTD-PTDPO混合方法模拟分析了圆锥喇叭馈源的单反射面天线及口径为1 m的卡塞格伦双反射面天线的脉冲时域特性，给出了反射面天线系统源的长方体网格及反射面照明区三角形网格的剖分要求，并将该要求应用于卡塞格伦双反射面天线的模拟计算中，所得计算结果与CST软件计算结果进行了比较，说明该网格剖分要求在口径天线近轴区远场PFDTD-PTDPO计算时有效可行。本文方法对大型反射面天线系统的时域特性分析具有一定的指导意义。

致谢

本文工作得到了西北核技术研究所黄文华研究员的指导和帮助，在此特别表示感谢！

［1］ 陈丰，郭陈江.宽角度扫描反射面天线辐射特性［J］.计算机仿真，2009，26（2）：50- 52.（CHEN Feng，GUO Chenjiang.Radiation characteristics of wide-angle scanning reflector antennas［J］.Computer Simulation，2009，26（2）：50- 52.）

［2］ARIAS A A M，LORENEO R M E，GARCIA-PINO A.A novel fast algorithm for physical optics analysis of single and dual reflector antennas［J］.IEEE Trans Magn，1996，32（3）：910- 913.

［3］KILDAL P-S，JOHANSSON M，HAGFORS T，et al.Analysis of a cluster feed for the arecibo trireflector system using forward ray tracing and aperture integration［J］.IEEE Trans Antennas Propag，1993，41（8）：1 019- 1 025.

［4］KILDAL P-S.Analysis of numerically specified multireflector antennas by kinematic and dynamic ray tracing［J］.IEEE Trans Antennas Propag，1990，38（10）：1 600- 1 606.

［5］ 黄立伟，金志天.反射面天线［M］.西安：西北电讯工程学院出版社，1986.（HUANG Li-wei，JIN Zhi-tian.Reflector Antenna［M］.Xi'an：Publishing House of Northwest Institute Telecommunication，1986.）

［6］CAMPO M A，DEL REY F J，BESADA J L，et al.SABOR：description of the methods applied for a fast analysis of horn and reflector antennas［J］.IEEE Antennas Propagat Mag，1998，40（4）：95- 103.

［7］ 廖勇，谢平，陆巍，等.超宽带Cassegrain双反射面天线研究［J］.强激光与粒子束，2007，19（8）：1 329- 1 332.（LIAO Yong，XIE Ping，LU Wei，et al.Cassegrain dual reflector antenna for UWB high power microwave［J］.High Power Laser and Particle Beams，2007，19（8）：1 329- 1 332.）

［8］ZHU X Q，WANG J G，CHEN Z G，et al.Hybrid PFDTDPTDPO method for computing transient far-fields of single reflector［C］／／International Conference on Microwave and Millimeter Wave Technology，Shenzhen，2012.

［9］ 朱湘琴，王建国，蔡利兵，等.大型双反射面天线近轴区辐射PFDTD-PTDPO模拟［J］.强激光与粒子束，2012，24（11）：2 703- 2 708.（ZHU Xiang-qin，WANG Jian-guo，CAI Libing，et al.FDTD-TDPO hybrid method for radiation simulation near axes of large dual reflector antennas［J］.High Power Laser and Particle Beams，2012，24（11）：2 703- 2 708.）

［10］ 朱湘琴，王建国，陈再高，等.单反射面天线模拟的并行FDTD-并行TDPO／时域PTDEEC混合方法［J］.现代应用物理，2014，5（3）：208- 213.（ZHU Xiang-qin，WANG Jianguo，CHEN Zai-gao，et al.Hybrid method for simulation of single reflector antenna based on parallel FDTD-parallel FDTD／time-domain PTDEEC［J］.Modern Applied Physics，2014，5（3）：208- 213.）

［11］RAMAHI O M.Near-and far-field calculations in FDTD simulations using Kirchhoff surface integral representation ［J］.IEEE Trans Antennas Propag，1997，45（5）：753- 759.

［12］ 葛德彪，闫玉波.电磁波时域有限差分方法［M］.3版.西安：西安电子科技大学出版社，2011.（GE De-biao，YAN Yu-bo.Finite-Difference Time-Domain Method［M］.3rd ed.Xi'an：Xidian University Press，2011.）

Requirement of Grid Division in PFDTD-PTDPO Hybrid Method for Large-Aperture Reflector Antennas

ZHU Xiang-qin1，WANG Jian-guo1，2，XING Xiao-yue1
（1.Northwest Institute of Nuclear Technology，Xi'an 710024，China；2.School of Electronic and Information Engineering，Xi'an Jiaotong University，Xi'an 710049，China）

A hybrid method combining parallelized finite-difference time-domain（PFDTD）and parallelized time-domain physical optics（PTDPO）is presented for computing the transient radiation far-fields of large reflectors.The example of a single reflector fed by horn is given，and the requirements of grid division for feed's domain and reflector domain are shown.According to the requirements，the far-fields of Cassergrain antenna are got，and the results agree with those by CST software.The requirements are also suitable for the method proposed in this paper to analyze the time-domain far-fields of various large-aperture reflector antennas with various feeds，including offset feed antennas.

time-domain；reflector antenna；parallelized FDTD；parallelized TDPO；grid division；near axis；far-field

TN823＋.27

A

2095- 6223（2015）02- 090- 08

2014- 12- 09；

2015- 04- 20

国家自然科学基金重点资助项目（61231003）

朱湘琴（1978－），女，江苏泰兴人，副研究员，博士，主要从事电磁场微波技术研究。

E-mail：zhuxiangqin＠nint.ac.cn