有监督不相关局部Fisher判别分析故障诊断
李 锋,王家序,汤宝平,邓成军
(1.四川大学制造科学与工程学院,四川成都610065;2.四川大学空天科学与工程学院,四川成都610065;3.重庆大学机械传动国家重点实验室,重庆400044)
有监督不相关局部Fisher判别分析故障诊断
李 锋1,王家序2,汤宝平3,邓成军1
(1.四川大学制造科学与工程学院,四川成都610065;2.四川大学空天科学与工程学院,四川成都610065;3.重庆大学机械传动国家重点实验室,重庆400044)
针对现有流形学习理论用于旋转机械故障诊断存在识别精度不高的问题,提出基于有监督不相关局部Fisher判别分析(Supervised Uncorrelated Local Fisher Discriminant Analysis,SULFDA)的新型故障诊断方法。首先构造全面表征不同故障特征的时频域特征集,再利用有监督不相关局部Fisher判别分析将高维时频域故障特征集化简为区分度更好的低维特征矢量,并输入到K-近邻分类器中进行故障模式辨识。有监督不相关局部Fisher判别分析在类标签指导下最小化同类流形的离散度并最大化异类流形的离散度来实现类判别,还施加了不相关约束条件使所提取的特征统计不相关,提高了针对旋转机械的故障诊断精度。深沟球轴承故障诊断实验验证了该方法的有效性。
故障诊断;旋转机械;时频域特征集;有监督不相关局部Fisher判别分析;流形学习
引 言
由于流形学习比传统数据挖掘方法更能体现观测数据的本质,在提取出主要变量的同时还获得了原始观测空间的真实拓扑结构[1-4],为实现对高维、非线性、多作用域的旋转机械故障特征数集进行特征约简和高精度的模式分类提供了更理想的解决思路。因此近年来流形学习理论研究及其在旋转机械状态监测与故障诊断中的应用研究受到越来越多的关注。目前典型的流形学算法包括:线性判别分析(Linear Discriminant Analysis,LDA)、局部保持映射(Locality Preserving Projections,LPP)[4]、正交邻域保持嵌入(Orthogonal Neighborhood Preserving Embedding,ONPE)[5]、局部Fisher判别分析(Local Fisher Discriminant Analysis,LFDA)[6]、半监督局部Fisher判别分析(Semi-supervised Local Fisher Discriminant Analysis,SSLFDA)[3]、归一化Laplacian矩阵有监督最优局部保持映射(Normalized Laplacian-based Supervised Pptimal Locality Preserving Projection,NL-SOLPP)[7]等。但这些方法都存在一些理论缺陷,对以解耦和分类为目的的维数约简应用来说都是欠佳的。例如,LDA和SSLFDA虽具备有监督/半监督特性,但它们输出的基矢量统计相关且互不正交,含有大量冗余成分,难以对数据的本征结构进行重构;LPP,ONPE和LFDA都是无监督方法,不具备类判别能力,不适用于存在诸多奇异数据点的情况[3];NL-SOLPP是一种新型有监督流形学习算法,但在有标记样本(即训练样本)数量较少情况下,其分类性能会有所衰退。本文研究了新型流形学习理论——有监督不相关局部Fisher判别分析(Supervised Uncorrelated Local Fisher Discriminant Analysis,SULFDA)。SULFDA是在类标签指导下通过最小化同类流形的离散度并最大化异类流形的离散度来实现类判别;其次SULFDA施加了不相关约束条件使所提取的特征统计不相关,因此SULFDA具有更好的特征提取和模式分类准确度。SULFDA输出的是不易被人理解和接受的特征矢量,为直观表达故障诊断结果,须借助人工智能技术建立降维后的特征矢量与故障模式之间的映射关系。本文用K-近邻分类器(KNearest Neighbors Classifier,KNNC)[5,8]来实现故障模式的识别。
本文提出了基于SULFDA的故障诊断方法:“时频域特征集-SULFDA-KNNC”,可实现更高的旋转机械故障诊断精度,具有较好的推广能力。
1 有监督不相关局部Fisher判别分析
为提高旋转机械故障诊断精度,本文作者在论文[2]中构造了11个时域特征参数和13个频域特征参数以提供比单域特征更多的故障特征信息。但高维时频域特征集不可避免地会掺杂一些冗余信息和干扰成分[9-11],因此需要采用维数化简方法对高维时频域特征集中状态敏感的特征进行二次提取,以获取维数低、敏感性高、独立不相关的主特征量。这里采用有监督不相关局部Fisher判别分析(SULFDA)来实现以上目的。以下是对SSLFDA的理论论述。
1.1 问题描述
假设采集n1个m维训练样本和n2个m维测试样本X={x1,x2,…,xn1,xn1+1,xn1+2,…,xn1+n2}∈Rm×(n1+n2)。该样本集存在一个潜在的d维非线性流形空间Rd,该空间Rd镶嵌在将其包裹其中的欧几里得空间Rm,其中d≪m。那么SULFDA的目的就是使用样本信息寻找投影矩阵V将样本集X转化为Rd空间的样本特征集Y=[y1,y2,…,yn1,yn1+1,yn1+2,…,yn1+n2],即

式中 V∈Rm×d。
1.2 有监督不相关局部Fisher判别分析理论
为模拟空间 Rm的局部几何结构,首先构造一个最近邻域图G:即对于每一个数据点xi,寻找它的k个最近邻域训练样本点。令N(xi)=x1i,x2i,…,{xki为xi}的k个最近邻域训练样本点集。通过只给邻域样本分配正亲缘值可以获得稀疏的亲缘矩阵,以提高计算效率。于是给最近邻域图G定义一个新的亲缘矩阵如下:

最近邻域图G及其亲缘矩阵A'表征了数据流形的局部几何关系。然而,该邻域图难以发掘数据之中的判别结构。为了能同时挖掘数据流形中的几何和判别结构,以下构造了两个最近邻域图,即同类流形邻域图GW和异类流形邻域图Gb。对于每一个数据点xi,其最近邻域点集N(xi)可以很自然地分解为两个子集:Nb(xi)和Nw(xi)。Nb(xi)包含的是与xi异类的邻域点,而Nw(xi)包含的是与xi同类的邻域点。显然,Nb(xi)∩Nw(xi)=ø且Nb(xi)∪Nw(xi)=N(xi)。
令W'lb为Gb的权值矩阵,W'lw为GW的权值矩阵。定义W'lb和W'lw如下:

式(3)和(4)中,li或lj∈{1,…,c}表示训练样本xi或xj(i=1,2,…,n1,j=1,2,…,n1)的类标签,n=n1+n2。式(3)和(4)表明,SULFDA在训练样本类标签的指导下对训练样本进行异类隔离和同类聚集处理,因此SULFDA是一种有监督学习机制。同类流形邻域图GW和异类流形邻域图Gb构造之后,当两个数据属于同类,那么它们存在于同一流形的置信度就很高,因此权值也就相对更大。
SULFDA的目标于是可以表述为:最小化同类邻域点集Nw中的每个样本与其k个最近同类邻域点之间的流形离散度,同时最大化异类邻域点集Nb中的每个样本与其k个最近异类邻域点之间的流形离散度。确定最优投影函数的一个最佳准则就是在适当约束条件下优化以下两个目标函数:

若邻域点xi和xj属于不同类,则针对异类流形邻域图Gb的目标函数(5)会形成严厉处罚机制以阻止异类邻域点xi和xj在低维嵌入空间的投影距离变得更近。通过代数推导,式(5)可以简化为

式中 S'lb为异类流形离散矩阵

若邻域点xi和xj属于同类,则针对同类流形邻域图GW的目标函数(6)会形成严厉处罚机制以阻止同类邻域点xi和xj在低维嵌入空间的投影距离拉得更远。通过代数推导,式(6)可以简化为


式中 S'lw为同类流形离散矩阵

于是,目标函数(6)可以表示如下

式(11)可等价转换为

此外,目标函数(5)可以重写为

现在就可以通过同时优化式(12)和式(13)来推导投影矩阵V,这一优化问题可表示如下

接下来,研究统计不相关约束。对低维嵌入式Y施加如下式所示的不相关约束

同时归一化vi以满足

式中 总离散矩阵St为


因此,结合式(14)和(18),SULFDA就可以表示成如下有约束最优化问题

从式(19)来看,SULFDA在不相关约束条件中还保持和强化了测试样本的全局几何结构,因此在少训练样本情况下,SULFDA仍能维持较好的故障特征分类特性,最后,对式(19)应用拉格朗日乘子法,同时令有约束最优化问题表达式对V的导数值为0。于是可最大化式(19)的投影向量v可通过求解以下广义特征值问题的最大特征值所对应的特征向量得到

令列向量v1,v2,…,vd为式(20)的解,即式(20)的特征值λ1≥λ2≥…≥λd所对应的特征向量。这样,嵌入式表示如下

式中 V=[v1,v2,…,vd]。
1.3 SULFDA算法总结
算法步骤:
步骤1:构造邻域图G并计算亲缘矩阵A'。
步骤2:构造类内流形邻域图Gw和类间流形邻域图Gb。
步骤3:根据式(3)和(4)计算局部类间流形权值矩阵W'lb和局部类内流形权值矩阵W'lw。
步骤4:根据式(8)和(10)构造局部类间流形离散矩阵S'lb和局部类内流形离散矩阵S'lw,并根据式(17)构造总离散矩阵St。
步骤5:计算(S'lb-S'lw)v=λStv的最大特征值所对应的特征向量,并将这些向量组合成最优投影矩阵V。
步骤6:n个数据点在d维嵌入空间中的坐标就由Y=VTX的列向量组给出。
2 故障诊断方法“时频域特征集-SULFDA-KNNC”
故障诊断方法“时频域特征集-SULFDAKNNC”实现流程如图1所示。

图1 故障诊断方法“时频域特征集-SULFDA-KNNC”流程Fig.1 Implementation process of fault diagnosis method“Time-frequency domain feature set-SULFDA-KNNC”
步骤如下:
(1)对反映不同故障特征的训练样本和测试样本信号构造11个时域特征参数和13个频域特征参数。(2)将11个时域特征参数和13个频域特征参数组合得到24维时频域特征集。(3)将训练和测试样本的24维时频域特征集同时输入SULFDA进行训练,求得投影矩阵V。(4)训练好的SULFDA再对训练和测试样本进行维数化简,分别得到d维非线性流形(特征矢量),1≤d<24。最优约简维数d的估计方法如下:首先对每一个训练样本xi(i=1,2,…,n1)的n1×n1维局部协方差矩阵Qi(r,s)=(xi-xr)T(xi-xs)进行特征分析;然后为每一个训练样本xi计算满足条件的约简维数di,λj为Qi的特征值;最后选择di中的最大值作为d值。(5)将训练和测试样本的d维特征矢量输入KNNC,KNNC根据训练样本的类标记和测试样本信息对测试样本分类决策,诊断出测试样本所对应的故障类别及其严重程度。
SULFDA在本故障诊断方法中起到承上启下的作用,它自动衔接时频域特征集和KNNC,并具有优良的特征提取和模式分类特性,是所提故障诊断方法实现较高诊断精度的关键技术。
但流形学习理论发展到现在(包括本文所研究的SULFDA),发挥的主要还是降维、去噪、特征二次提取的作用,还不具有完备的知识推理和拟合回归功能,暂不能作为终端分类决策工具使用。要想更为准确、直观地呈现故障辨识结果,还需借助人工智能、模式识别技术为经SULFDA降维之后的特征矢量辨识其隶属的故障类别。KNNC就是一种基于统计学的新型模式识别方法,不像多数有监督的模式识别方法在处理测试样本之前都有复杂的训练过程,KNNC直接利用训练样本的局部几何结构和类标签对待测样本进行分类决策,不仅计算量少,时效性好,同时保证了较好的模式识别能力,因此这里选择KNNC作为终端分类决策工具使用。KNNC的详细原理可参考文献[5]和[8]。
3 实例分析
3.1 深沟球轴承故障诊断
首先以深沟球轴承正常状态以及不同部位、不同程度故障的同步诊断实例验证本故障诊断方法的有效性。实验采用美国凯斯西储大学(Case Western Reserve University)电气工程实验室的滚动轴承故障模拟实验台[12]采集的轴承数据。该实验设备如图2所示[12],实验台包括一个2马力的电动机(图中左边),一个风扇(图中右边),一个扭矩传感器/译码器(图中间)等。待检测的轴承(驱动端轴承)支撑着电动机的转轴,型号为SKF6205-2RS(轴承内径为25 mm,外径为52 mm,厚度为15 mm,节径为39.04 mm,滚动体直径为7.94 mm,接触角为0°,滚动体个数为9)。该实验室以电火花加工的方式在3个轴承的外圈、内圈、滚动体上分别加工直径为0.178 mm,深为0.279 mm的小槽模拟轴承外圈、内圈、滚动体单点轻微(早期)裂纹;在另外3个轴承的外圈、内圈、滚动体上分别加工直径0.356 mm,深0.279 mm的小槽模拟轴承外圈、内圈、滚动体单点中度裂纹;在最后3个轴承的外圈、内圈、滚动体上分别加工直径0.533 mm,深0.279 mm的小槽模拟轴承外圈、内圈、滚动体单点严重裂纹。功率和转速通过扭矩传感器/译码器测得手动记录得到。实验时的转速为1 772 r/min。在驱动端的轴承座上方安装加速度传感器,通过16通道信号采集仪采集得到以上9类故障和正常状态的振动加速度信号。信号采样频率为48 k Hz。这里取9类故障和正常状态的振动信号数据各50组用于分析,每组数据长度为0.1 s。为模拟训练样本稀少的条件,从中仅随机抽取n1=10组用作训练样本,剩余n2=40组作为测试样本。图3为正常状态和9类故障测试样本时域波形。

图2 滚动轴承故障模拟实验台Fig.2 Fault simulation test-bed of rolling bearing
对每组训练和测试样本截取4 096个数据点用于测试样本的故障辨识,数据截取长度的选定遵循既要基本覆盖各类故障的特征频带又不增加诊断模型过多计算量的原则。诊断步骤如第3节所述。时域、频域特征参数总个数为24,也即SULFDA的输入特征维数为24。SULFDA的邻域大小设为k=20,SULFDA的约简维数即KNNC的输入维数位于区间d∈[1,k];KNNC的邻域大小设为K=7,故障模式与KNNC的期望输出的对应关系设定为:正常状态→1、外圈轻度裂纹→2、外圈中度裂纹→3、外圈严重裂纹→4、内圈轻度裂纹→5、内圈中度裂纹→6、内圈严重裂纹→7、滚动体轻度裂纹→8、滚动体中度裂纹→9、滚动体严重裂纹→10。以下从三个层次评估本故障诊断方法的性能:

图3 深沟球轴承正常状态、外圈轻微裂纹、外圈中度裂纹、外圈严重裂纹、内圈轻微裂纹、内圈中度裂纹、内圈严重裂纹、滚动体轻微裂纹、滚动体中度裂纹、滚动体严重裂纹故障(自上至下顺序)测试信号波形Fig.3 Waveform of the test signals of normal state,minor outer race crack,moderate outer race crack,severe outer race crack,minor inner race crack,moderate inner race crack,severe inner race crack,minor ball crack,moderate ball crack and severe ball crack(from up to down)
①在本故障诊断方法的维数化简和模式识别两个环节不做任何变动的前提下,将24维的时频域特征集的故障诊断精度与11维的时域特征参数集、13维的频域特征参数集等单一/单域方法进行对比。对比结果如表1所示。显然,时频域特征集所达到的测试样本诊断精度比时域特征集、频域特征集的单独作用都要好,表明时频域特征集全面挖掘轴承不同故障特征信息的能力(即推广能力)要优于单一/单域特征提取方法。
②将SULFDA的维数化简效果与ONPE,NL-SOLPP,LFDA,SSLFDA(化简维数d的变化区间与SULFDA设置相同)对比,对比结果如表2所示。显然,在少训练样本情况下,SULFDA由于采用了有监督学习机制,并对输出的低维嵌入式(特征矢量)施加了不相关约束,因此其对轴承正常状态和9种故障的辨识结果明显好于无监督机制下的ONPE和LFDA;也高于基于半监督学习机制但无不相关或正交约束的SSLFDA;在少训练样本情况下,有监督流形学习算法——NL-SOLPP的分类精度产生了明显衰退(若从本实验数据中随机抽取n1=20组作为训练样本使用,则NL-SOLPP对正常状态和9种故障的平均辨识精度可高达¯η=85.67%,但本文仅随机抽取n1=10组数据用于训练,结果其平均辨识精度仅为¯η=78.00%),也不及SULFDA的分类精度。表3是本故障诊断方法“时频域特征集-SULFDA-KNNC”的诊断结果抽样表;另外,所提故障诊断方法完成对测试样本的状态诊断所耗费的计算时间仅为20.855 s(实验验证在3 GHZ Intel CPU、4G RAM和MATLAB 2009的计算机配置环境下进行)。

表1 3种特征提取方法的故障诊断精度对比/%Tab.1 Comparison result of fault diagnosis accuracy obtained by three feature extraction methods/%

表2 5种流形学习算法维数化简后的故障诊断精度/%Tab.2 Comparison of fault diagnosis accuracy achieved by dimension reduction with five manifold learning algorithms/%
所提出的故障诊断方法对外圈轻微裂纹、外圈中度裂纹和外圈严重裂纹的诊断精度没有呈现预期的递增趋势的原因如下:从图3提供的时域波形图容易看出,外圈轻微裂纹信号的调制波周期/频率与外圈单点故障特征频率理论公式

计算出的结果fo=105.87 Hz非常吻合,即外圈轻微裂纹信号的调制波的周期性特征非常明显,然而外圈中度裂纹和外圈严重裂纹信号中的噪声干扰反倒大于外圈轻微裂纹信号,它们的周期性特征明显没有后者突出;同时外圈中度裂纹信号的信噪比也低于外圈严重裂纹信号的信噪比,因为前者的谐波特征明显又不如后者,所以造成对外圈轻微、中度和严重裂纹的识别精度分别为100%,65%和77.5%(但均在可接受的较高精度范围以内),而不是逐渐递增,这其实也间接验证了所提出方法的有效性,因为它准确反映了输入原始信号的信噪比质量。而内圈轻微裂纹、内圈中度裂纹和内圈严重裂纹的诊断精度和滚动体轻微裂纹、滚动体中度裂纹和滚动体严重裂纹的诊断精度也都没有呈现递增趋势的原因与外圈的情况类同。
③再将SULFDA维数化简后的故障诊断精度与不进行特征约简,将高维时频域特征集直接输入KNNC的诊断结果进行对比,结果见表4。由于高维混合域特征集不可避免地会掺杂一些冗余信息和干扰成分,造成不同状态或故障的高维时频域特征集之间具有某种统计相关性,因此若不进行特征约简处理,直接将高维时频域特征集输入KNNC进行故障诊断,正如表4第2列结果所示,不同类数据点之间的统计相关性造成了其自身特征分布结构的混叠与扭曲,进而引起故障诊断精度的下降。而经SULFDA维数化简后的诊断精度处于高水平,表明SULFDA在维数化简的同时消除了不同状态或不同故障信号的相关性,提高了对深沟球轴承正常状态和9种不同类型、不同程度故障的辨识精度。
以上轴承故障诊断实例充分验证了时频域特征集用于故障特征的全面准确挖掘、SULFDA用于自动维数化简与特征流形分类以及KNNC用于状态模式识别的有效性,突出的是SULFDA所发挥的关键性作用:构造时频域特征集的目的仅仅是保证故障信息量的广度,避免信息遗漏,故不可避免地会包含冗余指标,且对于不同的故障,冗余指标可能还有所不同,可能存在某一时/频域特征对于某故障而言是冗余指标,而对于另外的故障而言又是有用信息的问题。随着故障形式的复杂化和数据的批量化,靠借助传统的信号处理方法再来人工一一甄别各故障的有用特征和冗余信息显然是费力且低效的,实际上不太可行。而采用SULFDA是对各故障数据进行整体处理,它能够从高维、结构复杂、大批量的各类故障的时频域特征集中统一挖掘敏感性高、独立不相关、具有更好拓扑结构的低维主特征量(这是自动化的过程,无需引入人工分析),实验证明SULFDA明显提高了对深沟球轴承不同类型、不同程度故障的辨识精度。并且故障种类越复杂,数据量越大,SULFDA的高效性越突出。这就是SULFDA应用于旋转机械故障诊断的实际意义所在。
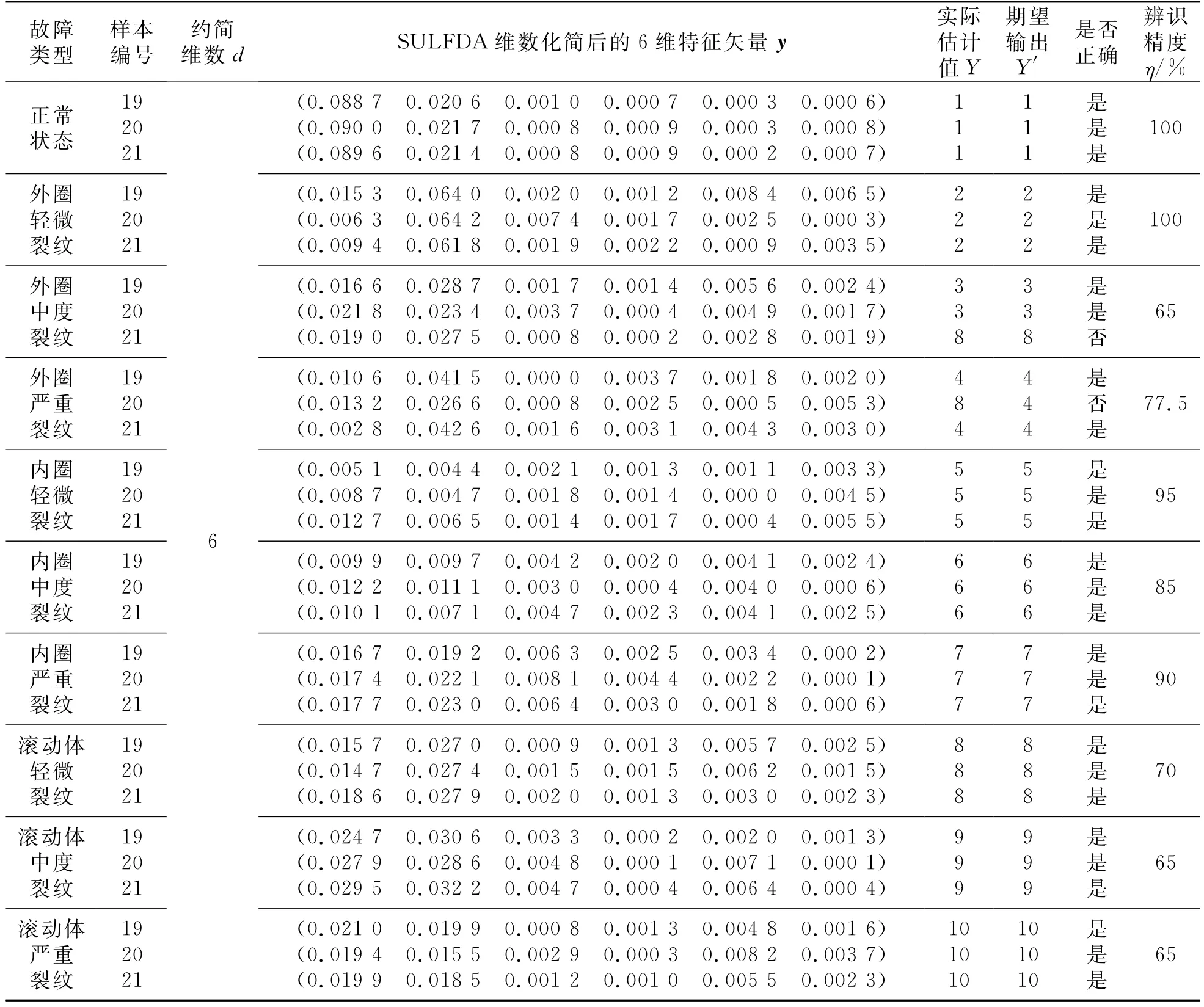
表3 故障诊断方法“时、频域特征集-SULFDA-KNNC”诊断结果抽样表Tab.3 Diagnosis results sampling table of fault diagnosis method“Time-frequency domain feature set-SULFDA-KNNC”

表4 SULFDA特征约简和不特征约简的诊断精度对比/%Tab.4 Fault diagnosis accuracy comparison using SULFDAfeature compression versus not using feature compression/%
3.2 深沟球轴承寿命状态识别
通过对某型号空间轴承不同的寿命阶段(即对早期故障出现之前的正常状态按相同时间间隔划分阶段)进行识别来进一步验证本故障诊断方法的泛化能力。该轴承的振动监测实验台如图4所示。本实验监测了3个同型号的空间轴承(分别编号为1、2、3)。3个轴承运行时转速恒为1 000 r/min,并都加载3 kg轴向载荷,采样频率25.6 k Hz。所监测的3个轴承的寿命状态有T1(已运行1~15天)、T2(已运行16~30天)、T3(已运行31~45天)、T4(已运行46~60天)、T5(已运行61~75天)、T6(已运行76~90天)、T7(已运行91~105天)等。这7种寿命状态都属于正常服役状态。

图4 空间轴承振动监测实验台Fig.4 Vibration test stand of space bearing
采集以上7种寿命状态的振动数据样本各25组(其中1号轴承9组、2号轴承8组、3号轴承8组),为模拟训练样本较少的条件,从1号轴承9组样本中仅随机抽取n1=8组作为训练样本,另外n2=17组(包括2号轴承样本、3号轴承样本和1号轴承剩余样本)作为测试样本,训练和测试样本长度都为4 096个数据点。本故障诊断方法在这里的参数设置与上例完全一致,寿命状态模式与KNNC的期望输出的对应关系设定为:T1→1,T2→2,T3→3,T4→4,T5→5,T6→6,T7→7。最后的寿命状态识别结果如表5所示。

表5 所提故障诊断方法对7个寿命阶段的识别精度/%Tab.5 Recognition accuracy of the proposed fault diagnosis method for seven life grades
结果表明所提故障诊断方法对该型号轴承7个寿命阶段的识别结果是正确的,并达到较高精度,说明该故障诊断方法泛化性较好,可直接用于旋转机械早期故障辨识;若再结合趋势分析理论,还可用于旋转机械剩余寿命预测。
考虑到完整的全寿命尺度下的轴承振动数据难以在短时间内获取(轴承使用寿命一般为2~3年)[13],故要实现在不完备经验数据条件下的寿命状态识别/剩余寿命预测,还要进一步研究趋势预测理论(如:神经网络、支持向量回归机等),以将本文方法“时频域特征集-SULFDA-KNNC”改进为具有趋势预测功能的理论模型:“时频域特征集-SULFDA-趋势预测理论”,并使用由过去时间(t-n),(t-(n-1)),…,(t-1)到当前时间t的低维特征矢量来提前预测(t+1)时间的低维特征矢量这一递推方式对将来时间(t+1),(t+2),…,(t+m)的特征进行趋势分析。再用本文方法“时频域特征集-SULFDA-KNNC”对预测的某将来时间(t+m)的低维特征矢量进行故障辨识,若该时间的信号特征属于某故障特征而非正常状态特征,则可以认为这一将来时间(t+m)为轴承失效时间。于是剩余寿命Tres=(t+m)-t=m。
4 结 论
(1)构造的时频域特征集可全面表征不同类型、不同程度故障的特征信息,具有较好的推广特性。(2)SULFDA在类标签指导下最小化同类流形的离散度并最大化异类流形的离散度来实现类判别,还施加了输出特征矢量不相关约束条件使所提取的特征统计不相关,发挥了自动简化高维时频域特征集并有效区分故障类别和程度的关键作用。(3)所提出的基于SULFDA的旋转机械故障诊断方法集成了时频域特征集在故障特征的全面提取、SULFDA在信息化简和KNNC在状态模式识别上的优势,实现了对深沟球轴承较高的故障诊断精度,也为今后进一步开展旋转机械寿命估计或剩余寿命预测提供了理论参考。
[1]Tianhao Zhang,Jie Yang,Deli Zhao,et al.Linear local tangent space alignment and application to face recognition[J].Neurocomputing,2007,70(7-9):1 547—1 553.
[2]Feng Li,Jiaxu Wang,Baoping Tang,et al.Life grade recognition method based on supervised uncorrelated orthogonal locality preserving Projection and K-nearest neighbor classifier[J].Neurocomputing,2014,138:271—282.
[3]Hong Huang,Jiamin Liu,Hailiang Feng,et al.Ear recognition based on uncorrelated local Fisher discriminant analysis[J].Neurocomputing,2011,74(17):3 103—3 113.
[4]Xiaofei He,Shuicheng Yan,Yuxiao Hu,et al.Face recognition using Laplacianfaces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3):328—340.
[5]李锋,汤宝平,董绍江.基于正交邻域保持嵌入特征约简的故障诊断模型[J].仪器仪表学报,2011,32(3):621—627.Li Feng,Tang Baoping,Dong Shaojiang.Fault diagnosis model based on feature compression with orthogonal neighborhood preserving embedding[J].Chinese Journal of Scientific Instrument,2011,32(3):621—627.
[6]Sugiyama Masashi.Dimensionality reduction of multimodal labeled data by local Fisher discriminant analysis[J].Journal on Machine Learning Research,2007,8:1 027—1 061.
[7]李锋,汤宝平,宋涛,等.归一Laplacian矩阵有监督最优局部保持映射故障辨识[J].机械工程学报,2013,49(13):100—107.Li Feng,Tang Baoping,Song Tao,et al.Fault identification method based on normalized Laplacian-based supervised optimal locality preserving projection[J].Chinese Journal of Mechanical Engineering,2013,49(13):100—107.
[8]Songbo Tan.An effective refinement strategy for KNN text classifier[J].Expert Systems with Applications,2006,30(2):290—298.
[9]Wong W K,Zhao HT.Supervised optimal locality preserving projection[J].Pattern Recognition,2012,45(1):186—197.
[10]李城梁,王仲生,姜洪开,等.自适应Hessian LLE在机械故障特征提取中的应用[J].振动工程学报,2013,26(5):758—763.Li Chengliang,Wang Zhongsheng,Jiang Hongkai,et al.Adaptive Hessian LLE in mechanical fault feature extraction[J].Journal of Vibration Engineering,2013,26(5):758—763[EB/OL].
[11]Xiaofei He,Deng Cai,Shuicheng Yan,et al.Neighborhood preserving embedding[A].Proceedings of 10th International Conference on Computer Vision[C].Beijing,China,2005:1 208—1 213.
[12]http://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-datacenter-website[EB/OL].
[13]王国彪,何正嘉,陈雪峰,等.机械故障诊断基础研究“何去何从”[J].机械工程学报,2013,49(1):63—72.Wang Guobiao,He Zhengjia,Chen Xuefeng,et al.Review of life prediction for mechanical major equipments[J].Chinese Journal of Mechanical Engineering,2013,49(1):63—72.
Fault diagnosis method based on supervised uncorrelated local Fisher discriminant analysis
LI Feng1,WANG Jia-xu2,TANG Bao-ping3,DENG Cheng-jun1
(1.School of Manufacturing Science and Engineering,Sichuan University,Chengdu 610065,China;2.School of Aeronautics and Astronautics,Sichuan University,Chengdu 610065,China;3.The State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing 400044,China)
Facing on the crucial problem that the fault diagnosis accuracy of current manifold learning theories for rotating machinery is not high enough,a novel fault diagnosis method based on Supervised Uncorrelated Local Fisher Discriminant Analysis(SULFDA)is proposed in this paper.The time-frequency domain feature set is first constructed to completely characterize the property of each fault.Then,SULFDAis introduced to automatically compress the high-dimensional time-frequency domain fault feature sets of training and test samples into the low-dimensional eigenvectors with better discrimination.Finallythe low-dimensional eigenvectors of training and test samples are input into K-nearest neighbors classifier(KNNC)to carry out fault identification.SULFDAachieves good discrimination ability by minimizing the within-manifold scatter and maximizing the between-manifold scatter under the supervision of class labels.Also,an uncorrelated constraint is put on SULFDAto make the extracted features statistically uncorrelated.Therefore,SULFDAimproves the fault diagnosis accuracy for rotating machine.The fault diagnosis experiment on deep groove ball bearings demonstrated the effectivity of proposed fault diagnosis method.
fault diagnosis;rotating machinery;time-frequency domain feature set;supervised uncorrelated local Fisher discriminant analysis;manifold learning
TH165+.3;TN911.2
A
1004-4523(2015)04-0657-09
10.16385/j.cnki.issn.1004-4523.2015.04.020
李锋(1982—),男,讲师。电话:18382385401;E-mail:lifeng19820501@163.com
王家序(1954—),男,教授,博士生导师。电话:18608013899;E-mail:xjw@scu.edu.cn
2014-10-17;
2015-05-12
国家自然科学基金青年基金资助项目(51305283);国家公派高级研究学者及访问学者(含博士后)项目(201406245021);高等学校博士学科点专项科研基金资助项目(20120181130012)

