基于连通导电理论的白云岩储层导电模型

宋延杰，张桠楠，唐晓敏，刘兴周，胡 凯

(1.东北石油大学地球科学学院，黑龙江大庆163318;2.非常规油气成藏与开发省部共建国家重点实验室培育基地，黑龙江大庆163318;3.中国石油辽河勘探开发研究院，辽宁盘锦124010)

雷家地区沙四段白云岩储层岩性主要为泥质白云岩，灰岩和砂砾岩所占比例很少.岩心分析有效孔隙度主要分布在4.0% ～19.0%，平均值为12.5%，岩心分析渗透率主要分布在2～60 mD，平均值为17.2 mD.储层黏土矿物类型主要以伊利石、伊蒙混层为主，伊蒙混层含量最高，达47.3%.在储层宏观裂缝观测中，层内缝与穿层缝孔隙较顺层缝孔隙发育，裂缝平均开度为15，在基质孔隙中以晶间孔、溶蚀孔为主.因此，该区块沙四段白云岩储层属于低孔隙度低渗透率储层，具有含泥质、孔隙－裂缝型双孔隙结构类型的特征.因此，需建立孔隙－裂缝型泥质白云岩导电模型.

1963 年，Warren 和 Root[1]提出了考虑裂缝孔隙度和基质孔隙度的由立方体单元组成的Warren－Root导电模型.1976 年，Aguilera[2]提出了基于孔隙－裂缝型双孔隙储层的导电模型，并指出双孔隙储层的胶结指数应小于基质的胶结指数.1983年，Rasmus[3]提出了考虑裂缝弯曲度与变裂缝孔隙指数的双孔隙模型.该模型中改进的胶结指数只适用于总孔隙度较低的情况，当总孔隙度大于某一值时，会出现储层胶结指数大于基质胶结指数的不正确结果.2000 年，Perez－Rosales等人[4]在 Warren－Root导电模型基础上，给出了在忽略基质导电时的基于纯裂缝介质导电方程，但由于忽略了基质导电，不能直接应用于孔隙－裂缝储层电导率计算，需要进行参数修正.2005年，徐朝晖等人[5]从次生孔隙角度出发，采用Maxwell－Garnet电导率模型研究双孔隙结构对碳酸盐岩储层导电性的影响，并计算次生孔隙度;推导出关于次生孔隙度函数的可变胶结指数，并将其代入阿尔奇公式求出储层的饱和度.2012年，赵辉等人[6]建立了基于裂缝倾角和裂缝曲折度的Aguilera孔隙指数计算模型，并用该孔隙指数替代储层胶结指数来求取单组系裂缝孔隙型储层饱和度.目前针对双重孔隙结构建立的储层导电模型[7－8]多是通过改进胶结指数利用阿尔奇公式[9]来计算储层含油饱和度.研究表明，孔隙－裂缝型岩石导电能力除与地层的岩性、物性、含油性及地层水电导率有关以外，还与地层水在孔隙中的分布形态有很大关联，而孔隙的大小、形态、裂缝的宽度、产状决定了地层水分布形态，也直接影响地层水的连通性.由于孔隙－裂缝型白云岩储层岩石的孔隙结构复杂，因此，地层水的连通性也会更加复杂.连通导电方程[10－13]通过引入相导电系数和水连通校正系数，既可以描述孔隙－裂缝型白云岩储层复杂的孔隙结构特征，又可以解释地层水的连通性、泥质附加导电对岩石导电性的影响，适用于描述孔隙－裂缝型白云岩储层的导电规律.

本文基于雷家地区白云岩储层特征和导电因素研究成果，结合连通导电理论特点，将地层分为基质相、裂缝相和黏土相，从而建立孔隙－裂缝型白云岩储层连通导电模型的体积模型;对3个导电相分别应用连通方程，得出各相电导率，然后，再用混合导电理论[14－15]将各相电导率与地层总电导率联系起来，建立了适用于雷家地区孔隙－裂缝型储层的连通导电模型;最后，用试油结果对导电模型的应用效果进行评价.

1 孔隙－裂缝型白云岩储层连通导电模型

1.1 纯岩石连通导电方程

Bernard Montaron[10]在考虑储层复杂孔隙结构特征和地层水连通性对岩石导电特性影响的基础上，引入水连通性校正系数和导电指数，提出了含油气纯岩石连通导电方程.其方程为:

其中:Ct为岩石电导率;Cw为地层水电导率;Sw为含水饱和度;φ为有效孔隙度;Xw为水连通性校正系数;μ为导电指数.

水连通性校正系数和导电指数均与水在介质中的分布状态和岩石中孔隙的几何形状有关，且水连通性校正系数可解释水在孔隙中的连通作用.水连通性越好，Xw越小.当Xw≈0时，式(1)可简化为:

1.2 孔隙－裂缝型白云岩储层连通导电模型的建立

针对本区储层存在着孔隙型和裂缝型两种孔隙类型以及含有泥质等特征，结合连通导电理论特点，将本区储层划分为基质相、裂缝相和黏土相.其中:基质相包括骨架颗粒、水和油气;裂缝相包括泥浆滤液和残余油气;黏土相包括黏土束缚水和干黏土颗粒.图1给出了本区连通导电模型的体积模型，其物质平衡方程为:

其中:Vma、Vdc、Vcl分别为骨架颗粒、干黏土颗粒、黏土在岩石中的体积含量，小数;φ、φw、φwb、φh、φxo、φhr分别为基质有效孔隙度、基质含水孔隙度、黏土水孔隙度、含油孔隙度、裂缝含水孔隙度和裂缝含残余油气孔隙度，小数;φf和φt为裂缝孔隙度和总孔隙度，小数.

地层水导电为离子导电，黏土相中黏土水导电机理为阳离子交换导电，所以地层水和黏土水的电导率不同.对基质相、裂缝相和黏土相分别应用连通导电方程，可得各相电导率为:

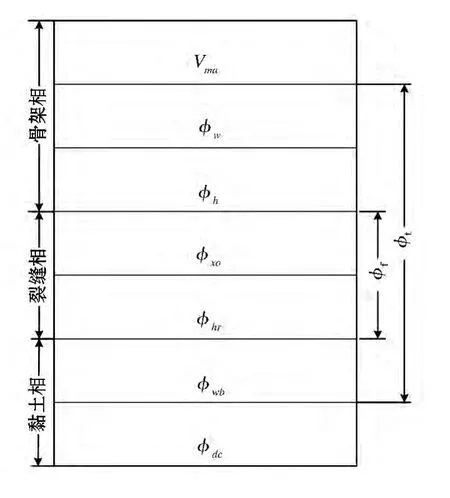
图1 双孔隙储层连通导电模型的地层体积模型

设为岩石总电导率，X1、X2、X3分别为基质相、裂缝相和黏土相的体积分数，根据混合导电定律[14]，得出:

其中:X1=Vma+ φw+ φh，X2= φf，X3=Vcl.

将式(5)代入式(6)，整理得:

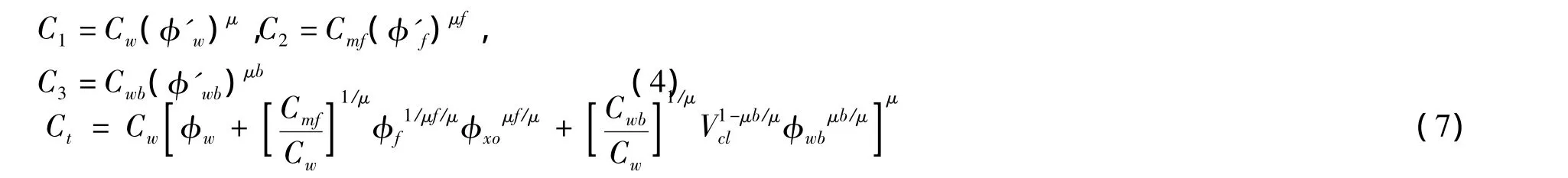
将φw=φtSwt－φxo－φwb代入式(7)得:

则式(8)可简化为:

其中:Xw为基质中水连通校正系数，Xwf为裂缝中泥浆滤液的连通校正系数，Xwb为黏土水连通校正系数，Swt为总含水饱和度.

式(9)即为基于连通导电理论的孔隙－裂缝型白云岩储层导电模型.

2 孔隙－裂缝型白云岩储层连通导电模型理论分析

2.1 模型的理论验证

对于未侵入的饱含水纯白云岩，有Vcl=0，Vdc=0，φwb=0，φw= φ，φxo= φf，Cw=Cmf，式(9)可简化为:

1)当 φt=1.0 时，无论 μ 为何值，有 F=1.0，与地层因素定义在孔隙度等于1.0时F恒等于1.0的情况相符.

2)当只含有基质孔隙，即φf=0时，有F=1/φμ.该模型即可简化为孔隙型纯岩石的阿尔奇公式.

2.2 模型的影响因素分析

这里主要讨论基质相导电指数、裂缝相导电指数、裂缝孔隙度值的变化对孔隙－裂缝型白云岩储层连通导电模型的影响.

2.2.1 基质相导电指数的变化对导电模型的影响

假设 Vcl=0.3，φt=0.115，φf=0.01，φb=0.05，Rw=0.48Ω·m，Rwb=0.11Ω·m，Rmf=0.2Ω·m，μf=1.4，μb=1.6，φhr=0.01，φwb=0.06.图2给出了μ分别为 1.6，1.8，2.0，2.2，2.4 的 Rt与 Swt及I与Swt的交会图，从图2中可以看出，在Swt一定时，Rt和I随μ的增大而增大.

图2 基质相导电指数变化对模型的影响

2.2.2 裂缝相导电指数的变化对导电模型的影响

假设 Vcl=0.3，φt=0.115，φf=0.01，φb=0.05，Rw=0.48Ω·m，Rb=0.11Ω·m，Rmf=0.2Ω·m，μ =2.0，μb=1.6，φhr=0.01，φwb=0.01.图3给出了μf分别为 1.0，1.2，1.4，1.6，1.8 时的 Rt与Swt及I与Swt的交会图，从图3中可以看出，在Swt一定时，Rt和I随μf变化较小.

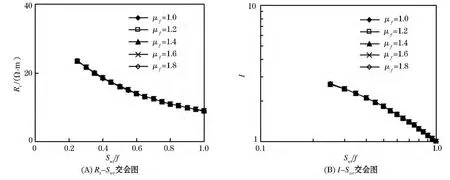
图3 裂缝相导电指数变化对模型的影响

2.2.3 裂缝孔隙度的变化对导电模型的影响

假设 Vcl=0.3，φt=0.115，φb=0.05，Rw=0.48Ω·m，Rwb=0.11Ω·m，Rmf=0.2Ω·m，μ =2.0，μf=1.4，μb=1.6，φwb=0.06.图4给出了 φf分别为0.005，0.01，0.015，0.02，0.025 时的 Rt与 Swt及I与Swt的交会图，从图4中可以看出，在Swt一定时，Rt随φf的增大而减小，I随φf的增大而增大.

图4 裂缝孔隙度变化对模型的影响

3 应用效果分析

为了应用孔隙－裂缝型白云岩连通导电模型确定白云岩储层含油饱和度，必须确定模型中的各个参数.利用深侧向电阻率资料和岩心分析数据，建立该区泥质含量计算关系式;利用岩心分析孔隙度和声波测井资料建立了基质孔隙度的计算关系式;利用岩心分析孔隙度和渗透率资料，建立了基质孔隙度与基质渗透率之间的关系式;结合裂缝测井响应特征，给出了利用双侧向测井求取高、低角度裂缝孔隙度的方法;利用双侧向电阻率资料计算裂缝宽度，进而计算固有裂缝渗透率，给出了求取裂缝渗透率的方法.由于该区缺少密闭取心井岩心分析含水饱和度资料，不能用最优化技术求解各相导电指数，所以利用试油结论得到的经验值作为基础参考值.

图5 雷A井测井解释成果图

利用建立的连通导电模型对1口井进行了饱和度处理，并与试油结果进行对比.图5为雷A井的解释成果图，该井段处理的33、34、35号层为试油层位，3个层合试，日产油3.82 t，试油结论为油层.处理结果可知，33号层孔隙度为10.3%，渗透率为10.4 mD，含水饱和度为58.8%，解释为低产油层;34、35号层孔隙度为14.7%，渗透率为26.2 mD，含水饱和度为31.9%，解释为油层，解释结果与试油结果相符.

4 结论

1)连通导电方程能够描述孔隙型基质、裂缝及泥质导电规律，而混合导电定律能够将三者结合起来，从而建立了岩石电导率表达式.该导电模型能很好地描述孔隙－裂缝型泥质白云岩储层的导电规律.

2)对于未侵入的饱含水白云岩，当 φt=1.0时，地层因素恒为1.0;当只含有基质孔隙时μ=1.0，模型简化为孔隙型纯岩石的阿尔奇公式;当只含有裂缝孔隙且时，模型简化为水平裂缝纯岩石地层因素与孔隙度关系.

3)实际井资料解释结果与试油结论对比，表明用本文提出的模型计算的孔隙－裂缝型泥质白云岩储层的饱和度是合理的，解释结果与试油结论相符.

[1]WARREN J E，ROOT P J.The behavior of naturally fractured reservoirs[J].SPE Journal，1963，3(3):245 －255.

[2]AGUILERA R.Analysis of naturally fracture reservoirs from conventional well logs[J].Journal of Petroleum Technology，1976，28(7):764－772.

[3]RASMUS J C.A variable cementation exponent m of carbonate pore systems[J].The Log Analyst，1983，24(6):13 －23.

[4]PEREZ R，MERCADO D，CRUZHERNAN D，et al.New formulation for formation resistivity factors of fractured porous media[C]//Mexico:SPE International Petroleum Conference and Exhibition，SPE 58991，2000.

[5]徐朝晖，焦翠华，王绪松，等.碳酸盐岩地层中双孔隙结构对电阻率及胶结指数的影响[J].测井技术，2005，29(2):115－117.

[6]赵 辉，石 新，司马立强.裂缝性储层孔隙指数、饱和度及裂缝孔隙度计算研究[J].地球物理学进展，2012，27(6):2639－2645.

[7]孙建孟，王克文，李 伟.测井饱和度解释模型发展及分析[J].石油勘探与开发，2008，35(1):101－107.

[8]潘宝芝，张丽华，单刚义，等.裂缝和孔洞型储层孔隙模型的理论进展[J].地球物理学进展，2006，21(4):1232－1237.

[9]ARCHIE G E.The electrical resistivity log as an aid in determining some reservoir characteristics[J].Trans.AIME，1942，146:54－62.

[10]MONTARON B.Fractals，percolation theory and the stability of Archie’s‘m’exponent[C]//AbuDhabi:The SPWLA Topical Conference on“Low Resistivity Pay in Carbonates”，2005.

[11]MONTARON B.A quantitative model for the effect wettability on the conductivity of porous rocks[C]//Manama:SPE Middle East Oil and Gas Show and Conference，SPE 105041，2007.

[12]MONTARON B.Connectivity theory－a new approach to model the electrical conductivity of non－Archie reservoir rocks[C]//Edinburgh:SPWLA 49th Annual Logging Symposium，2008.

[13]宋延杰，幺丽娜，徐广田，等.长垣地区低孔隙度低渗透率砂岩储层中连通导电模型的应用[J].测井技术，2012，36(4):345－351.

[14]BERRYMAN J G.Mixture theories for rock properties，rock physics and phase relations－a handbook of physical constants[M].Washington D C:American Geophysical Union，1995.205－228.

[15]张斌弛，马世忠，刘 钰.P油田H油组参数解释研究[J].哈尔滨商业大学学报:自然科学版，2014，30(2):211－214，228.