弹体侧向喷流流动干扰数值模拟与分析

李澍达

(西北工业大学航空学院，西安710072)

结合推力矢量技术和反作用控制系统原理的侧向喷流控制技术，是一种提高导弹机动性和快速反应能力的控制方法.高压的喷流喷入弹体外流场时，两种流动会产生相互作用，从而在喷口附近的上下游区域形成复杂的干扰流场，从而引起弹体气动性能的变化[1].

从20世纪60年代开始，欧美发达国家对侧向喷流控制技术进行了大量基础性的实验研究和理论分析，并在数值研究方面已经覆盖到从欧拉方程的计算到N－S方程的计算[2].目前，国内对喷流干扰流场的研究尚处于起步阶段.张涵信等人对二维干扰流场进行了数值模拟，得到了干扰流场的波系结构[3];王江锋等人采用有限元方法求解二维欧拉方程，得到喷流轨迹和喷流横截面变化等结果[4];庞勇等人通过求解三维N－S方程研究了高超音速来流中干扰流场的波系结构，并分析相关音速对气动力的影响[5].

现阶段导弹侧喷控制的喷口布局主要有两种，一种是以紫苑系列导弹为代表，弹身上的四个液态发动机喷口呈叉字布局;另一种是以爱国者III型导弹为代表，多个固态发动机喷口沿周向和展向均匀分布.对于后者，喷口周向位置的不同，是否会对喷流控制效果产生影响，并未得到国内外学者的广泛关注.本文主要根据爱国者III型导弹喷口布局，针对不同喷口位置的侧向喷流干扰流场进行数值模拟，得出放大因子，并对流场气动特性进行了分析.

1 数值方法

1.1 控制方程

三维可压缩N－S方程组在笛卡尔坐标系下可以写为:

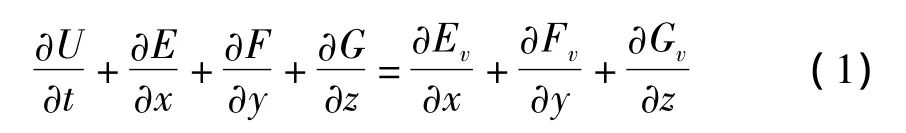
其中:U 为守恒变量;E，F，G 为对流项;Ev，Fv，Gv为黏性项，黏性系数由Sutherland公式确定.

1.2 数值方法

有限体积的基本思想是将计算划分为若干个单元体，每个单元体用 Ω(i，j，k)表示.将方程(1)在每个单元体上离散，则有

其中:Ui，j，k是变量 U 在 Ω(i，j，k)上的平均量;Vi，j，k是 Ω(i，j，k)的体积;－ Ri，j，k为离散后的对流项;Rv，i，j，k为离散后的黏性项.

采用AUSM格式对进行离散;为了保证格式的精度以及保持格式的一致性，黏性项利用梯度及散度的积分表达式进行离散.

2 湍流模型

S－A湍流模型由于其容错功能好，处理复杂流动的能力强，已得到广泛应用.S－A模型不同于其他一些单方程模型，不是从两方程模型经过简化得到的，而是直接根据经验和量纲分析，从简单流动开始，直接得到最终的控制方程.相对于B－L模型，S－A模型在每个时间步长内都要对整个流场多求解一组偏微分方程，故所花费的时间更多，但是S－A模型对分离流动的模拟能力要比B－L模型好.相对于两方程模型S－A模型又有计算量小和稳定性好的优点，故本文采用S－A湍流模型进行数值模拟分析.

3 方法验证

选取ONERA M6机翼作为方法验证算例.ONERA M6机翼由于其几何外形简单，但是又具有较复杂的流动现象，比如当地超声速流、激波、和湍流边界层分离等，使得其已经成为国际上标准的跨声速外流的CFD验证算例，得到极为普遍的使用.本文所选状态为马赫数 0.839 5，迎角 3.06°.使用AUSM格式进行计算，图1展示了AUSM格式的计算结果与实验值的比较图，分别选取了6个展向占位上的压强系数与实验值进行对比，可见计算结果与实验结果相符良好，验证了方法的可行性.

4 模型和计算网格

本文研究外形为尖拱柱光弹体并在尾部加一组叉字布局弹翼的翼身组合体，图2给出了模型和计算网格示意图.

模型总长为1 900 mm，圆柱部分直径为200 mm.喷口安置在距头部顶点1 200 mm处，直径为20 mm.计算网格在模型轴向，法向和半周向分别取126、41、41个网格点，并对喷口附近网格进行了局部加密，以保证分析结果的精确度.为了避免大幅增加总体网格量，此处网格使用了非结构棱柱网格.本文中，定义x轴为模型对称轴，z=0平面为对称面，喷口位置沿模型周向绕对称轴移动，与对称面的夹角为β.

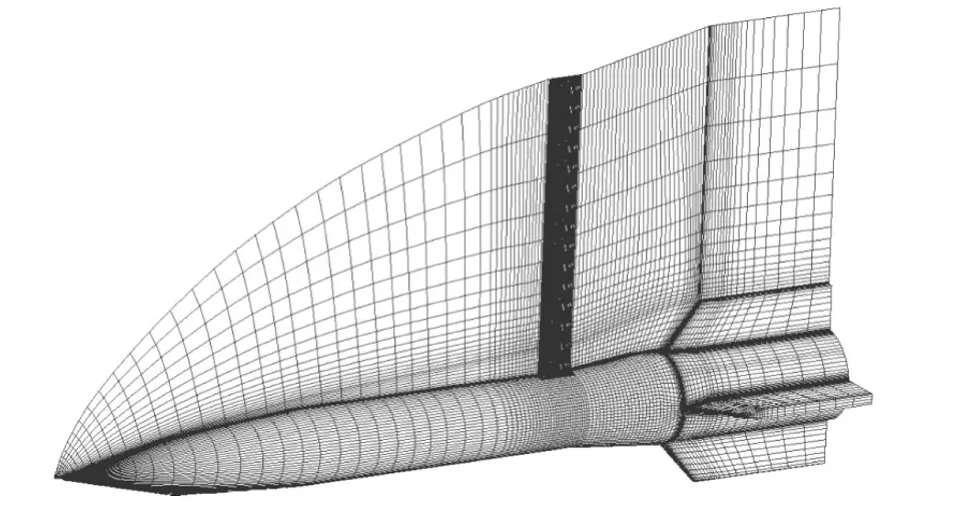
图2 模型及计算网格示意图

5 计算结果及分析

5.1 计算条件

来流条件:M∞=2.5，To∞=300 K，Po∞=1.731 MPa;

喷流条件:Mj=1.0，Toj=250.81 K.

在Poj/Po∞=5和Poj/Po∞=15两种喷流总压比下，对 β =0°，β =22.5°，β =45°这三种喷口位置的流场干扰进行数值模拟.

5.2 流场分析

图3为对称面上的压力等值线.由图4可知，来流与侧向喷流在喷口附近形成较强的流场干扰，使得来流在喷口前分离，产生了分离激波和弓形激波，分离区内压力升高，形成一个高压区.喷流的高压气体在喷口附近因为过度膨胀产生了一个悬挂于流场中的马赫盘，并在喷口后方，再次分离，形成了一个低压区.

图3 压力等值线(M∞ =2.5，Poj/Po∞ =15，β =0°)

对于侧向喷流干扰流场的分析，最有意义的是喷口前的分离区(即高压区)，以及喷口后的分离区(即低压区)的分布情况.通过对称面内的流场压力分布云图和弹体上表面(喷口所在表面)的压力分布曲线可以较为直观的得出压力分布情况.图4为不同喷流总压比下，流场压力分布图.由图4可知，随着喷流压力的增大，即总压比(Poj/Po∞)的增大，喷口前的高压区明显增大，喷流穿透高度也明显增加，弓形激波的激波角增大.喷流压力的增大，也使得喷口后的低压区有一定程度的增大，但相比于高压区，低压区的变化较小.

图4 流场压力分布(M∞=2.5，β=0°)

图5为Poj/Po∞=15时，不同β下，流场压力分布图.由图可以看出β的增大，导致喷口前的高压区增大，喷口后的低压区变化并不明显，故给出了壁面压力分布图.

图5 流场压力分布(M∞=2.5，Poj/Po∞=15)

图6为喷口附近的壁面压力分布图.由此可较为清晰的看到，相较于 β =0°，β =22.5°和 β =45°时，壁面高压区影响范围虽有一定的减小，却更为集中，在喷口前变化更为剧烈，高压区的压力也有所增大.喷口后的低压区也有一定的增加，但变化幅度不大.喷口前高压区对喷流的控制效果带来正面影响，喷口后的低压区则正好相反.因此，喷口位置偏离弹翼，即喷口与对称面夹角β(小于45°)的增大，会带来更好的喷流控制效果.下面将通过由计算得出的喷流放大因子的变化，进一步验证该结论.

5.3 放大因子

侧向喷流的干扰效果主要通过喷流放大因子K来体现

上式中，下标 j，on/j，off代表有 /无喷流作用的情况，为弹体受到的总气动力，为没有喷流时弹体受到的气动力，为喷流的推力.式(3)主要反映流场的干扰效应对喷流推力所产生的放大效果.根据国外的相关计算和实验结果表明，低空大气层内的的喷流放大因子往往小于1[6].现有K的计算结果如表1所示.而Poj/Po∞=5时，放大因子K小于1，说明喷流实际提供的侧向力小于喷流本身的推力，喷流得到了抑制.在Poj/Po∞=15时，侧向喷流干扰效应更为明显，随着β的增大，放大因子K由小于1逐渐增加至1以上，表明经过与来流的相互干扰，喷流推力逐渐由被抑制到被放大，喷流控制效果增强[7].这也一定程度上证明了翼的存在会对侧向喷流流场干扰产生影响.

表1 不同条件下放大因子K的比较

6 结语

本文对超音速流场下的弹－翼组合体侧向喷流干扰流场进行了数值模拟，得到了不同喷流总压比，不同喷口位置下，流场的气动特性以及喷流放大因子.结果表明，在喷流干扰区域更偏离弹翼时，即喷口与对称面的夹角越大，喷流放大因子越大，喷流的控制效果越好.从而也间接证明了翼对于侧向喷流干扰流场具有一定程度的影响.

[1]CHAMBERLAIN R R.Calculation of three－dimensional jet interaction flow fields[R].AIAA 90－2099，1990.

[2]GRAHAM M J，WEINACHT P.Numerical simulation of lateral control jets[R].AIAA 99－0510，1999.

[3]张涵信，刘 君.超声速主流中横向喷流场的激波—漩涡结构的数值模拟[J].空气动力学学报，1991，3:9－14.

[4]王江锋，杨 生.横向喷流与超音速主流干扰流场的数值模拟[J].航空学报，2001，6:78－83.

[5]庞 勇，贺国宏.高超声速侧向喷流干扰流场数值模拟[J].空气动力学学报，2000，18(S1):115－120.

[6]GRAHAM M J，WEINACHT P，BRANDEIS J.A numerical investigation of supersonic jet interaction for finned bodies[R].AIAA 2000－0768.

[7]高 清，李 潜.某非圆截面导弹的动态特性分析[J].哈尔滨商业大学学报:自然科学版，2012，28(4):497－501.