生活中的一次函数应用

赵黎明

一次函数是初中数学的核心内容，也是重要的基础知识和重要的数学思想，与生活中的实际问题有着极为广泛的联系，是联系数学知识与实际问题间的纽带和桥梁，也是中考数学试卷中不可缺少的重要内容.解决这类问题的关键是在理解题意、分析数量关系的基础上，正确找出已知量与未知量间的相等关系，把生活中的语言转化为代数式，从而建立数学模型.

一、分段计费问题

例1 某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过20 m3时，按2元/ m3计费；月用水量超过20 m3时，其中的20 m3仍按2元/ m3收费，超过部分按2.6元/ m3计费.设每户家庭用水量为x立方米时，应交水费y元.

（1）分别求出 和 时， 与 的函数表达式；

（2）小明家第二季度交纳水费的情况如下：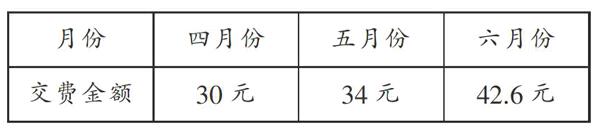

小明家这个季度共用水多少m3？

答：小明家这个季度共用水53m3.

【点评】收费问题与我们的生活息息相关，如水费问题、电费问题、话费问题等，这些收费问题往往根据不同的用量，采用不同的收费方式.以收费为题材的数学问题多以分段函数的形式出现在中考试题中，解答时需分段讨论.

二、方案选择问题

例2 有甲、乙两家通迅公司，甲公司每月通话的收费标准如图1所示；乙公司每月通话收费标准如表1所示.

（1）观察图1，甲公司用户月通话时间不超过100分钟时应付话费金额是 元；甲公司用户通话100分钟以后，每分钟的通话费为 元；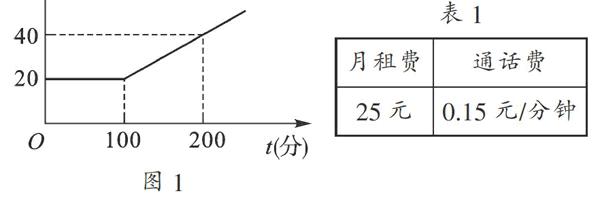

（2）李女士买了一部手机，如果她的月通话时间不超过100分钟，她选择哪家通迅公司更合算？如果她的月通话时间超过100分钟，又将如何选择？

【解析】（1）当0≤t≤100时，话费金额y=20；当t>100时，利用待定系数法求函数表达式得y=0.2t， 从而得出，甲公司用户月通话时间不超过100分钟时应付话费金额是20元；当甲公司用户通话100分钟以后，每分钟的通话费为0.2元；

【点评】方案选择问题是我们生活中常遇到的问题，人们要对各种方案有所选择和决策.本题是通过观察图像和表格中的信息，构建一次函数的数学模型，同时又与一元一次方程和一元一次不等式相结合解决问题.

三、行程问题

例3 从甲地到乙地，先是一段平路，然后是一段上坡路，小明骑车从甲地出发，到达乙地后立即原路返回甲地，途中休息了一段时间，假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km.设小明出发x h后，到达离甲地y km的地方，图中的折线OABCDE表示y与x之间的函数关系.

（1）小明骑车在平路上的速度为 km/h；他途中休息了 h；

（2）求线段AB、BC所表示的y与x之间的函数关系式；

（3）如果小明两次经过途中某一地点的时间间隔为0.15h，那么该地点离甲地多远？

【解析】（1）由速度=路程÷时间就可以求出小明在平路上的速度，就可以求出返回的时间，进而得出途中休息的时间；

【点评】行程问题是一个常规的问题，而新课下的行程问题，与原来行程问题的应用题完全不同，往往与图像、图形、表格等结合在一起，不仅考查学生的数学知识，而且考查学生的识图能力和数形结合的数学思想. 本题考查了行程问题的数量关系的运用，待定系数法求一次函数的解析式的运用，一元一次方程的运用，解答时根据题意结合图象说出其图象表示的实际意义，求出一次函数的解析式是关键.

小试身手

1. 为了庆祝商都正式营业，商都推出了两种购物方案.方案一：非会员购物所有商品价格可获九五折优惠，方案二：如交纳300元会费成为该商都会员，则所有商品价格可获九折优惠.

（1）以x（元）表示商品价格，y（元）表示支出金额，分别写出两种购物方案中y关于x的函数解析式；

（2）若某人计划在商都购买价格为5880元的电视机一台，请分析选择哪种方案更省钱？

2.星期天，小强骑自行车到郊外与同学一起游玩，从家出发2小时到达目的地，游玩3小时后按原路以原速返回，小强离家4小时40分钟后，妈妈驾车沿相同路线迎接小强，如图，是他们离家的路程y（千米）与时间x（时）的函数图像.已知小强骑车的速度为15千米/时，妈妈驾车的速度为60千米/时.

（1）小强家与游玩地的距离是多少？

（2）妈妈出发多长时间与小强相遇？