一次函数与方案设计问题探究

吴克

一次函数是最基本的函数，它与一次方程、一次不等式有密切联系，在实际生活中有广泛的应用。尤其利用一次函数的增减性等有关知识可以在某些经济活动中的方案设计和选择提供帮助，作出最佳的决策。近几年来一些省市的中考或竞赛试题中也时常出现这方面的应用题，这些试题新颖灵活，具有较强的时代气息和很强的选拔功能。下面以几道中考题为例说明一次函数在中考中的重大作用.

一、分配方案的设计

例1.（2011四川攀枝花）某经营世界著名品牌的总公司，在我市有甲、乙两家分公司，这两家公司都销售香水和护肤品.总公司现香水70瓶，护肤品30瓶，分配给甲、乙两家分公司，其中40瓶给甲公司，60瓶给乙公司，且都能卖完，两公司的利润（元）如下表.

（1）假设总公司分配给甲公司x瓶香水，求：甲、乙两家公司的总利润W与x之间的函数关系式；

（2）在（1）的条件下，甲公司的利润会不会比乙公司的利润高？并说明理由；

（3）若总公司要求总利润不低于17370元，请问有多少种不同的分配方案，并将各种方案设计出来.

考点：一次函数的应用.

专题：函数思想.

分析：（1）设总公司分配给甲公司x瓶香水，用x表示出分配给甲公司的护肤品瓶数、乙公司的香水和护肤品瓶数，根据已知列出函数关系式.（2）根据（1）计算出甲、乙公司的利润进行比较说明.（3）由已知求出x的取值范围，通过计算得出几种不同的方案.

（1）设A型汽车安排 辆，B 型汽车安排 辆，求 与 之间的函数关系式.

（2）如果三种型号的汽车都不少于4辆，车辆安排有几种方案？并写出每种方案.

（3）为节约运费，应采用（2）中哪种方案？并求出最少运费.

考点：一次函数的应用；一元一次不等式组的应用.

专题：优选方案问题.

分析：（1）利用三种汽车一共运输120吨山货可以得到函数关系式；

（2）利用三种汽车都不少于4辆，可以得到有关x的不等式组，利用解得的不等式组的解得到安排方案即可；（3）根据题意得到总运费与自变量x的函数关系式，求得其最值即可.

答：为节约运费，应采用 ⑵中方案一，最少运费为37100元。

点评：本题考查的是用一次函数解决实际问题，此类题是近年中考中的热点问题.注意利用一次函数求最值时，关键是应用一次函数的性质；即由函数y随x的变化，结合自变量的取值范围确定最值.

三、营销方案的设计

（1）、若全部资金用来购买彩电和洗衣机共100台，问商店可以购买彩电和洗衣机各多少台？

（2）、若在现有资金160000元允许的范围内，购买上表中三类家电共100台，其中彩电台数和冰箱台数相同，且购买洗衣机的台数不超过购买彩电的台数，请你算一算有几种进货方案？哪种进货方案能使商店销售完这批家电后获得的利润最大？并求出最大利润.（利润=售价-进价）

考点：一次函数的应用.

专题：优选方案问题.

分析：（1）根据题意商店购买彩电x台，则购买洗衣机（100﹣x）台，列出一元一次方程，解方程即可得出答案；

解答：（1）设商店购买彩电x台，则购买洗衣机（100﹣x）台.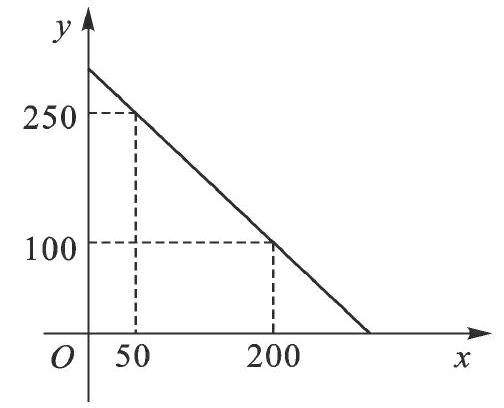

点评：本题主要考查了一次函数的实际应用，解答一次函数的应用问题中，要注意自变量的取值范围还必须使实际问题有意义.

四、优惠方案的设计

例4.（2013·遂宁）四川省第十二届运动会将于2014年8月18日在我市隆重开幕，根据大会组委会安排，某校接受了开幕式大型团体操表演任务.为此，学校需要采购一批演出服装，A、B两家制衣公司都愿成为这批服装的供应商.经了解：两家公司生产的这款演出服装的质量和单价都相同，即男装每套120元，女装每套100元.经洽谈协商：A公司给出的优惠条件是，全部服装按单价打七折，但校方需承担2200元的运费；B公司的优惠条件是男女装均按每套100元打八折，公司承担运费.另外根据大会组委会要求，参加演出的女生人数应是男生人数的2倍少100人，如果设参加演出的男生有x人.

（1）分别写出学校购买A、B两公司服装所付的总费用y1（元）和y2（元）与参演男生人数x之间的函数关系式；

（2）问：该学校购买哪家制衣公司的服装比较合算？请说明理由.

考点：一次函数的应用.

专题：方案选择问题.

分析：（1）根据总费用=男生的人数×男生每套的价格+女生的人数×女生每套的价格就可以分别表示出y1（元）和y2（元）与男生人数x之间的函数关系式；

根据条件可以知道购买服装的费用受x的变化而变化，分情况讨论，当y1>y2时，当y1=y2时，当y1

点评：本题考查了根据条件求一次函数的解析式的运用，运用不等式求设计方案的运用，解答本题时根据数量关系求出解析式是关键，建立不等式计算优惠方案是难点.

五、进货方案设计

例5.（2013年贵州黔东南）某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒，乙品牌的进货单价是甲品牌进货单价的2倍，考虑各种因素，预计购进乙品牌文具盒的数量y（个）与甲品牌文具盒的数量x（个）之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中，甲有120个时，购进甲、乙品牌文具盒共需7200元.

（1）根据图象，求y与x之间的函数关系式；

（2）求甲、乙两种品牌的文具盒进货单价；

（3）若该超市每销售1个甲种品牌的文具盒可获利4元，每销售1个乙种品牌的文具盒可获利9元，根据学生需求，超市老板决定，准备用不超过6300元购进甲、乙两种品牌的文具盒，且这两种品牌的文具盒全部售出后获利不低于1795元，问该超市有几种进货方案？哪种方案能使获利最大？最大获利为多少元？

考点：一次函数的应用.

专题：方案选择问题。

分析：（1）根据函数图象由待定系数法就可以直接求出y与x之间的函数关系式；

（2）设甲品牌进货单价是a元，则乙品牌的进货单价是2a元，根据购进甲品牌文具盒120个可以求出乙品牌的文具盒的个数，由共需7200元为等量关系建立方程求出其解即可；

点评：本题考查了待定系数法求一次函数的解析式的运用，列一元一次方程列一元一次不等式组解实际问题的运用，解答时求出第一问的解析式是解答后面问题的关键.

综上所述，利用一次函数的图象、性质及不等式的整数解与方程的有关知识解决了实际生活中许多的方案设计问题，如果同学们能切实理解和掌握这方面的知识与应用，对解决方案问题的数学题是很有效的.