Sylvester定理的应用
曾庆怡(韶关学院 数学与统计学院 ,广东 韶关512005)
Sylvester定理的应用
曾庆怡
(韶关学院 数学与统计学院 ,广东 韶关512005)
摘要:结合高等代数专题教学经验和近年高等代数的考研真题,总结了利用矩阵的Sy1vester定理来解决有关矩阵特征值和行列式问题的方法,供相关人员参考.
关键词:Sy1vester定理;特征值;行列式
在高等代数考研中,矩阵的特征值和特征向量以及行列式计算越来越重要,有些试题要么用常规方法来解决计算量会很大,要么就无从下手.本文使用矩阵的Sy1vester定理来解决这两类问题.
Sy1vester定理[1]:设A是数域F上的m×n矩阵,B是n×m矩阵,m≥n,AB的特征多项式是fAB(λ),BA的特征多项式是fBA(λ),则有:

这里Em表示m阶单位矩阵.该定理表明对数域F上的任意矩阵A,B,AB和BA有相同的非零特征值;特别地,如果m=n,则有|λE-AB|=|λE-BA|,即AB与BA有完全相同的特征值(特征向量未必相同!).
1 求矩阵的特征值
设A是n阶矩阵,如果A能够分解为两个矩阵B,C的乘积,A=BC,且CB特征值容易求出时,可以考虑使用Sy1vester定理.特别地,如果矩阵A的秩r(A)≤2,则A的特征值很容易求出.
如果矩阵A可以表示为kE±BC的形式,其中r(BC)≤2,则矩阵BC的特征值可以使用Sy1vester定理求出,进而求出A的特征值.
例1设b=(b1,b2,…bn)T是n维非零向量,求矩阵:

的特征值和特征向量.[中南大学,2002].
解因为A的任意3阶子式全是零,所以r(A)=2.于是:


当λ=0时,由于r(A)=2,AX=0有n-1个线性无关的解向量,即为A的属于特征值0的特征向量.因为b为非零向量,存在bi≠0.于是AX=O与下面方程组同解:
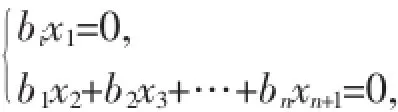
取x2,x3,...,xn+1为自由未知量,依次令x2,x3,...,xn+1为bi,其余为0,可得A的属于特征值0的特征向量:



例2设α,β是欧氏空间Rn的两个正交列向量,且|α|=|β|=2.设En为n阶单位矩阵,A=En+ααT+ββT,求A的特征多项式.[苏州大学,2007]
解因为:

其中B=(α,β)是n×2矩阵,C=BT,且CB=4E2,由Sylvester定理有:

例3设α,β是n维列欧氏空间Rn的两个正交的单位向量.证明矩阵A=αβT+βαT相似于对角矩阵diag(1,-1,0,...,0).[燕山大学,2012].
证令B=(α,β),C=(β,α)T则B,C分别为n×2,2×n矩阵.由于α,β正交,α,β线性无关,从而r(B)=r(C)=2.因为A=BC,由Sy1vester定理有:
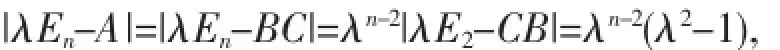
即A的特征值是λ1=1,λ2=-1,λ3=...=λn=0.因为A为实对称矩阵,A可对角化,从而A相似于对角矩阵diag(1,-1,0,...,0).
例4证明下列矩阵是半正定矩阵:

证A是实对称矩阵,且A=nE-B其中B是元素全是1的n阶矩阵.令α=(1,1…,1),则B=αTα.设λ 是A的任意特征值,则由Sy1vester定理有:

于是A的特征值是n-1重根n和一重根0,因此A是半正定的.
2 计算矩阵的行列式
使用Sy1vester定理可以计算这样的行列式,该型行列式可以写成数量矩阵kE与两个秩为2或1的矩阵乘积的和,这种行列式使用Sy1vester定理计算.另外kE可以换成可逆的对角矩阵.
例5计算以下行列式:

解该行列式的矩阵可以写成单位矩阵和秩为2的矩阵的和.令:

由Sy1vester定理,有:
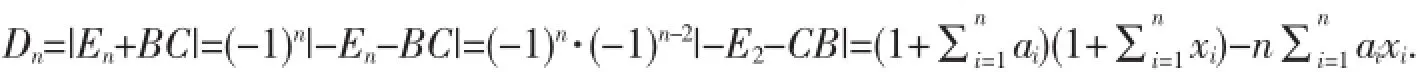
例6计算以下行列式:

解令A=diag(x1,x2,…,xn),α=(a1,a2,…,an),则A可逆,且Dn=|A+αTα|=|A||E-(-A-1)αTα|.由Sy1vester定理有:

参考文献:
[1]毛纲源.线性代数解题方法和技巧[M].长沙:湖南大学出版社,1987.
[2]王萼芳,石生明.高等代数[M].3版.北京:高等教育出版社,2003.
(责任编辑:邵晓军)
中图分类号:O153
文献标识码:A
文章编号:1OO7-5348(2O15)12-OOO5-O3
[收稿日期]2015-06-19
[作者简介]曾庆怡(1967-),男,湖南邵阳人,韶关学院数学与统计学院副教授,博士;研究方向:环与模范畴.
APPlications of Sylvester Theorem
ZENG Qing-yi
(Schoo1 of Mathematics and Statistic,Shaoguan University,Shaoguan 512005,Guangdong,China)
Abstract:In this PaPer,combining with the author's exPerience in advanced a1gebra teaching and entrance examination of graduate students of advanced a1gebra,some methods of aPP1ications of Sy1vester theorem in ca1cu-1ations of eigenva1ue of matrix and of determinants have been given.
Key words:Sy1vester theorem;eigenva1ues;determinants

