CHUY320型强夯机动力学计算
李丽敏,刘 冲LI Li-min, LIU Chong(北京南车时代机车车辆机械有限公司,北京 102249)
CHUY320型强夯机动力学计算
李丽敏,刘 冲
LI Li-min, LIU Chong
(北京南车时代机车车辆机械有限公司,北京 102249)
[摘 要]CHUY320型强夯机在实际运用过程中,臂架起臂工况和重锤突然释放工况的载荷条件比较复杂,给强度校核与疲劳评估带来困难;为了确定其载荷条件、弹簧选择是否满足要求、各部件之间的相互作用力等,特建立动力学模型,通过数值仿真计算获得动态载荷及各部件之间相互作用力,弹簧的压缩量及受力等,为弹簧的选型,整机的疲劳寿命分析提供载荷谱及结构优化提供理论依据。
[关键词]强夯机;动力学计算;臂架起臂工况;重锤释放工况
1 概 述
强夯法就是利用起重设备将重锤提升到一定的高度,然后使重锤自由下落,以巨大的冲击能量作用在地基上,使地基压变以达到加固地基的一种地基处理技术。这种方法的显著特点是夯击能量大,因此影响深度大,同时具有工艺简单、效果显著、设备简单、费用低廉、质量控制容易、适用土层范围广、施工周期短等突出优点[1]。
CHUY320型强夯机有两种典型的工作工况,在设计时需要重点考虑。
1)带龙门架起臂工况:这个工况时,龙门架与臂架平放在地面上,二者用销轴相连,通过变幅卷扬收缩钢丝绳的长度,实现起臂。这一过程中,由于绷绳需要克服龙门架与臂架的重力和其保持静止的惯性力,在龙门架和臂架起臂瞬间,臂头上所受拉力较大而且呈非线性变化,传统力学方法较难获取该载荷历程。
2)落锤工况:强夯机施工时,强夯机的每一工作循环均发生突然卸载工况,在突然卸载瞬间,由于变幅系统和整机的弹性作用,臂架系统反弹振荡,极易发生臂架后翻与折断,甚至发生翻车的事故[2]。
由于目前针对的强夯机设计计算尚无响应的设计标准,依然依靠经验和试验方法来确定。用虚拟样机技术,采用多体动力学仿真的方法是解决这一问题的良好手段。
2 起架工况建模及数值仿真分析
臂架起臂的过程是变幅卷扬通过对变幅钢丝绳的收缩实现的,这个过程中,随着臂架与地面夹角的变化,臂架所受的拉力也呈非线性变化。通过动力学仿真获取这一过程中的载荷变化历程,作为有限元的输入条件,获取这一过程中臂架的强度状况。
2.1 起架工况动力学建模
起架动力学仿真模型如图1所示,初始状态为臂架与地面保持水平,龙门架与臂架通过鼻头处的销轴连接,另一端与地面接触;龙门架的质量为12.727t。臂架和龙门架靠绷绳拉起,由于涉及到绷绳与滑轮的缠绕过程,该过程很难在仿真模型中实现,因此采用简化的模型,利用相对驱动来代替绷绳的提拉作用。

图1 起架工况动力学仿真模型
由于臂架的启停加速度数据难以获得,只有中间匀速部分的参数可以获得。因此本次计算根据驱动速度
V=Vs/n
其中,Vs为变幅卷扬钢丝绳线速度;n为变幅卷扬钢丝绳倍率。
代入数据可得V=80.8÷12=6.73m/min=112.22mm/s。启停加速过程设置为1s,则启停加速度为112.22mm/s2。驱动速度定义曲线如图2所示。
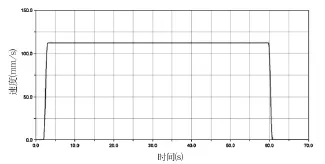
图2 起架工况位移驱动速度变化曲线
2.2 起架工况动力学分析
仿真总时间为70s,前2s是静态平衡状态,2~3s是启动过程,3~59.8s是匀速起吊过程,59.8~60.8s是停止过程。单股绷绳拉力的变化曲线如图3所示。图3中1 153.3kN的峰值是由于112.22mm/s2的启动加速度造成的。后面随着龙门架和臂架的逐渐抬起,力臂减小,绷绳需要克服的弯矩也在减小,所以绷绳上的拉力逐渐减小。如图3所示,最大瞬态拉力为1 153.3kN,最大稳态拉力为1 028.9kN,臂架的支撑点有2个,由于对称结构,两边的受力基本是一致的,因此只给出了单个支撑点的受力曲线。
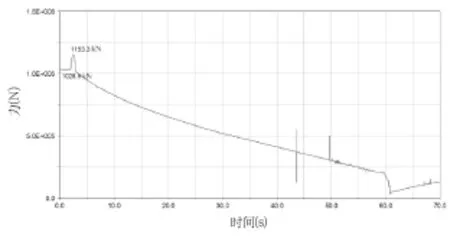
图3 单股绷绳拉力的变化曲线
臂头对龙门架的拉力变化曲线如图4所示。图4可以看出,在臂头提拉龙门架的瞬间,启动加速度导致此处有一个81.69kN的峰值,随着龙门架与地面夹角的逐渐增大,龙门架重心与臂头的力臂略有增大,所以此处的力也稳中有增,在龙门架逐渐接近与地面垂直的时候,臂头把龙门架提离地面并调整到合适位置,然后放到地面上,所以在地面摩擦力和龙门架重力的联合作用下,此处出现数值振荡并出现峰值122.92kN,待龙门架被最终放到地面上时,臂头所受拉力急剧下降,并最终达到稳定。
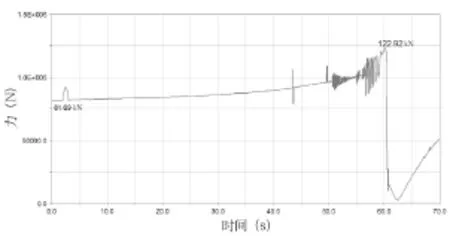
图4 臂头对龙门架的拉力变化曲线
为了得到臂架支撑点处的载荷情况,以作为有限元模型的边界条件,特提取了臂架支撑处垂向力和横向力随时间的变化曲线,从图5、图6可知,臂架支撑点垂向力最大值分别为瞬态值281kN和稳态值201kN,对应横向力分别为118kN和116kN,臂架支撑点横向力最大值578.25kN,对应垂向力-4.02kN,这3组数据分别作为臂架起臂工况对应臂架相应角度的边界条件,施加到支撑点处,以校核此处臂架的强度和刚度情况以及臂架支撑点处的强度情况。
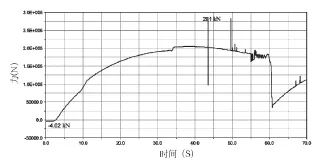
图5 臂架支撑点垂向力变化曲线
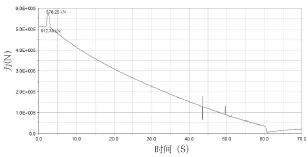
图6 臂架支撑点横向力变化曲线
3 回弹工况建模及数值仿真分析
3.1 回弹工况动力学建模
强夯机的落锤过程中臂架会产生较剧烈的回弹动作,载荷条件比较复杂,给强度校核与疲劳评估带来困难;为了研究该动作下臂架所承受的冲击力、弹簧选择是否满足设计要求、各部件之间的相互作用力等,特建立了回弹工况的动力学模型。通过数值仿真计算获得动态载荷及各部件之间相互作用力,弹簧的压缩量及受力等,并分析其倾覆稳定性。
回弹过程中能量主要来源于绷绳的弹性变形能逐渐释放并转换成臂架结构的动能,然后转换为弹簧的势能,从而产生臂架地来回振荡,最终通过摩擦及碰撞作用逐渐耗散能量,使臂架停下来的过程。因此绷绳的弹性属性对回弹动作起决定性影响,较准确的绷绳弹性模量是该工况数值计算的核心。
CHUY320型强夯机回弹工况动力学仿真模型如图7,其中夯锤质量为18t,以钢的密度7.82E-6kg/mm3,计算得整个臂架为5.74t,相应的3个轴的转动惯量分别为IXX=5.809E+11,IYY=5.805E+11,IZZ=3.214E+9。驾驶室与行走机构固定连接,行走机构与地面固定连接。由于钢丝绳只能受拉力,而不能受压力作用,本次计算采用分段弹簧来模拟钢丝绳的特性,每段弹簧长度为1 000mm,共分28段,如图8所示。钢丝绳作为受拉柔性构件,当运动的钢丝绳绕过滑轮、圆盘和卷筒时,或跑车的行走轮通过钢丝绳时,钢丝绳出现附加的压应力和弯曲应力,其应力状态是极其复杂的。从文献报道看[3],大多是对钢丝绳进行测试并统计出弹性模量变化范围。
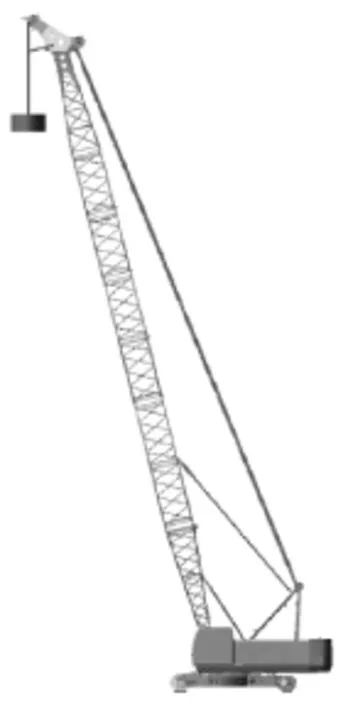
图7 回弹工况动力学仿真模型
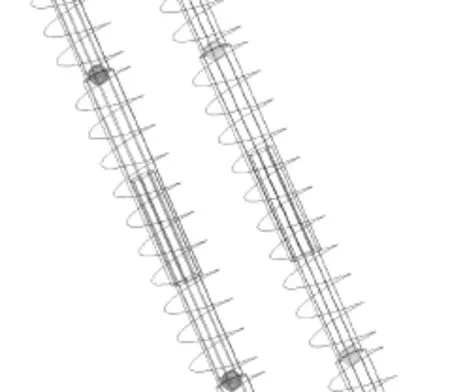
图8 钢丝绷绳分段弹簧模拟模型
由于CHUY320型强夯机采用的绷绳型号为6×19W+IWR-1870,查阅钢丝绳相关标准可知,钢芯钢丝绳等效弹性模量为ES=0.932E+5MPa,绷绳的直径为36mm。根据这些参数就可以求得每一段弹簧的等效刚度。
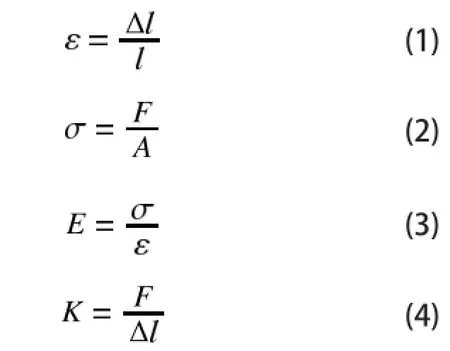
其中,ε为应变;σ为工作应力;E为弹性模量;K为刚度;l为原始长度;Δl为伸长量;F为拉力;A为力的作用面积。
根据公式(1)~(4)式可以得出分段弹簧刚度为
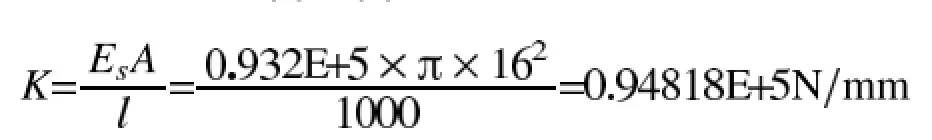
由于实际的防倾杆为两段弹簧串联作用,如图9。本模型用一段弹簧来模拟所以其刚度相当于串联弹簧的刚度K=156.175N/mm,自由长度为420mm,最大压缩量为120mm。下拉杆弹簧刚度为K=312.35N/mm。自由长度为405mm,最大压缩量为45mm。
3.2 回弹工况动力学分析
仿真时间取10s,前两秒为静平衡,在2s末,夯锤脱落,臂架开始回弹,2s之后是回弹动态响应过程。由于本次计算未考虑绷绳的结构阻尼,能量耗散比较慢,所以停止前所经历的回弹次数比实际多。

图9 防倾杆弹簧接触模拟模型
图10表明,夯锤脱落之前,绷绳上的拉力为恒定值170.96kN,随着夯锤脱落,臂架回弹,绷绳所受拉力从最大值变为0,并随着臂架的前后振荡,绷绳上的值也从0到峰值之间变化,但没超过恒定值。此载荷变化历程可以作为疲劳分析的载荷谱,施加到有限元模型上,进行疲劳寿命分析。
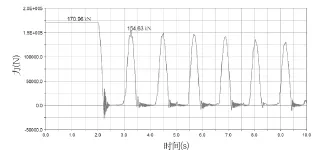
图10 绷绳拉力变化曲线
图11、图12分别为防倾杆上杆处弹簧拉力和弹簧压缩量的变化曲线。由图可以看出,在夯锤脱落之前,弹簧处于自由状态,随着夯锤脱落,弹簧被压缩,最大压缩量为113.905mm,其上的压力最大为17.79kN。由于该弹簧的压缩极限为120mm,所以上杆处弹簧的选型满足设计要求。
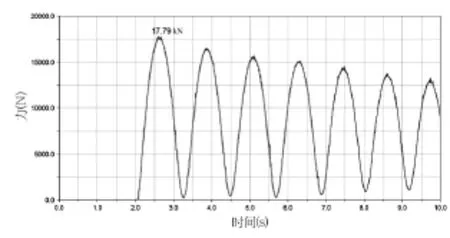
图11 防倾杆上杆处弹簧拉力变化曲线
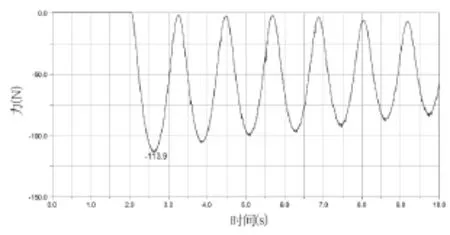
图12 防倾杆上杆处弹簧压缩量变化曲线
图13、图14分别为防倾杆下杆处弹簧拉力和弹簧压缩量的变化曲线。由图可以看出,在夯锤脱落之前,弹簧处于自由状态,随着夯锤脱落,弹簧被压缩,最大压缩量为36.21mm,其上的压力最大为11.31kN。由于该弹簧的压缩极限为45mm,所以下杆处弹簧的选型满足设计要求。
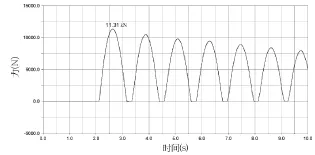
图13 防倾杆下杆处弹簧拉力变化曲线
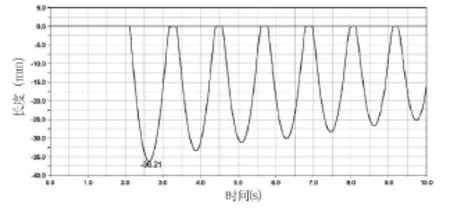
图14 防倾杆下杆处弹簧压缩量变化曲线
图15、图16分别为夯锤脱落时,臂架支撑点垂向力和横向力的变化曲线。可以得到,在夯锤脱落之前,垂向力和横向力的最大值分别为306.25kN和72.35kN,夯锤脱落之后,垂
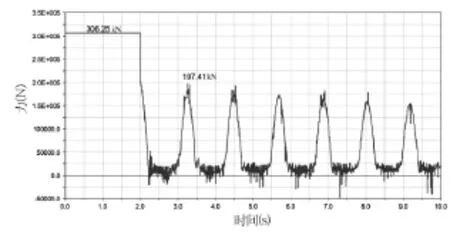
图15 臂架支撑点垂向力变化曲线
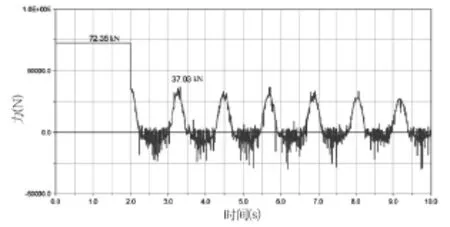
图16 臂架支撑点横向力变化曲线
向力和横向力的最大值分别降为197.41kN和72.35kN,由于强夯机的工作载荷是典型的交变载荷,设计计算时不但要考虑到最大载荷,还需要根据下图提供的载荷历程来进行疲劳寿命分析。
4 结 论
通过本次CHUY320型强夯机动力学仿真计算可以得出如下结论。
1)起臂过程中,单股绷绳最大稳态拉力为1028.9kN,发生在臂架与水平面平行的时刻。
2)回弹过程中上拉杆和下拉杆弹簧的压缩量分别为113.1mm、36.2mm均未超过120mm、45mm的极限压缩量,因此弹簧的选型满足设计要求。
3)回弹过程中,臂架支撑点处和防倾杆处所受的力为典型的交变载荷,设计计算时,除了考虑峰值载荷之外,还要考虑交变载荷引起的疲劳破坏。
[参考文献]
[1] 何长明.强夯法的发展现状与展望[J].中国水运,2010,10(4):186-187.
[2] 高顺德,谢高兰,曹旭阳,等.基于刚柔耦合模型的强夯机动力学分析[J].中国工程机械学报,2011,9(3):284-289.
[3] 吴沂隆.钢丝绳弹性模量的研究[J].福建林业科技[J].2003,30(3):62-64.
(编辑 贾泽辉)
[中图分类号]TU67
[文献标识码]B
[文章编号]1001-1366(2015)04-0049-04
[收稿日期]2015-03-30
Dynamic calculation of CHUY320 dynamic compaction machinery

