一类葡萄酒质量评估模型研究
康 卫,盛晓艳
(阜阳师范学院信息工程学院,安徽阜阳236041)
一类葡萄酒质量评估模型研究
康 卫,盛晓艳
(阜阳师范学院信息工程学院,安徽阜阳236041)
主要利用主成分分析和多元线性回归分析得出了酿酒葡萄和葡萄酒的理化指标与葡萄酒质量的函数关系,利用残差分析,检验出多元线性回归模型是可行性的.最后把理化指标分析法和感官评价相结合构建出红葡萄酒质量评估模型,使评价模型更加客观完善.
主成分分析法;相关性分析;多元线性回归分析;残差检验
红葡萄酒是驰名国内外的一种饮料酒,也是国家大力生产发展中酒类产品的重点发展品种.目前在国际市场上,红葡萄酒的质量评估依然以专业评酒员的评定为依托.由于评酒员间存在评价尺度、评价位置和评价方向等方面的差异,不同评酒员对同一酒样的评价结果不同,导致评价结果的不客观性.因此我们急需一套客观的、完善的评估模型来评估红葡萄酒质量.
1 研究材料和数据
1.1 材料
选取不同成品的红葡萄酒和酿酒红葡萄各27种,得到相关理化指标的数据.
1.2 数据来源
2012年全国大学生数学建模A题:第二组红葡萄酒品尝评分表、酿酒红葡萄和红葡萄酒的理化指标.
2 模型的建立和求解
2.1 模型概要
本文把感官评价法和理化指标分析法结合起来构建红葡萄酒质量综合性评估模型.把理化指标分析法加入到传统的红葡萄酒评价模型中,这样降低了在感官评价中因个体差异对结果可靠性造成的影响,使评估结果更加可靠,评估模型更加完善.在具体评估时,应该合理确定感官评价结果和理化指标评估结果各自所占的权重.
2.2 模型的求解
2.2.1 主成分分析模型的建立
主成分分析是把原来多个变量化为少数几个综合指标的一种统计分析方法,从数学角度来看,这是一种降维处理技术.根据实际需要从中选取载荷较大的理化指标.
具体步骤如下:
(1)数据的标准化处理
利用公式:
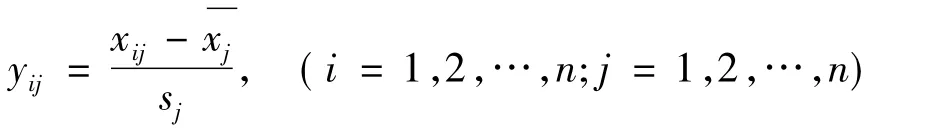
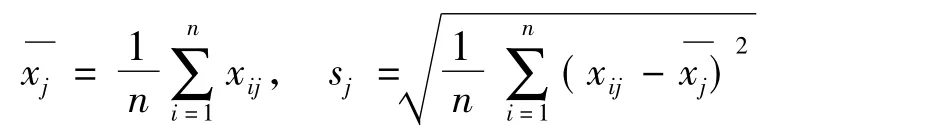
其中xij为第i种样品葡萄第j个指标的值为第j个指标的样本均值和样本标准差.
(2)计算相关系数矩阵

rij(i,j=1,2,…,p)为原变量xi和xj的相关系数,其中rij=rji,计算公式为:
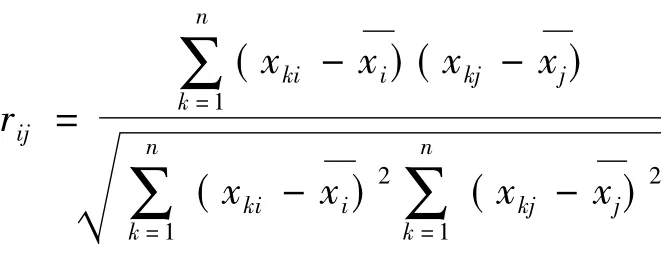
(3)计算特征值和特征向量
(4)计算主成分贡献率及累计贡献率

取累计贡献率达到70%的特征值λ1,λ,2,…,λm所对应的第1,2,…,m(m≤p)个主成分;
(5)计算主成分载荷
设它们降维处理后的综合指标,即新变量为z1,z2,…,zm(m≤p),

其中lij=p(zi,xj)=(i,j=1,2,…,p)
2.2.2 用主成分分析法分析酿酒红葡萄和红葡萄酒载荷较大的理化指标
分别对27种酿酒红葡萄和红葡萄酒一级理性指标进行主成分分析后,得到五个主成分,累计贡献率大于85%,具有统计学上的意义.
(1)利用Matlab软件得到酿酒红葡萄主因子载荷矩阵如表1(Xi表示红葡萄的一级理化指标因子)

表1 正交旋转后的主因子载荷矩阵(红葡萄)
取得前五个主成分,各理化指标因子的二维载荷主平面数据表.可知:对于主成分Z1中各个因子载荷值,从正方向上看,比较大的是果皮质量,从负方向上看比较大的是花色苷,单宁,分别为-0.827 3,-0.507 4.依次分析五种主成分,得出载荷较大的理化指标因子为:花色苷鲜重,DPPH自由基,总酚,白藜芦醇,总糖,可溶性固形物,干物质含量,果皮质量.我们分别令它们为自变量X1,X2,X3,…,X8.
(2)利用Matlab编程运行得到主因子载荷矩阵如表2(Xi表示红葡萄的一级理化指标因子)
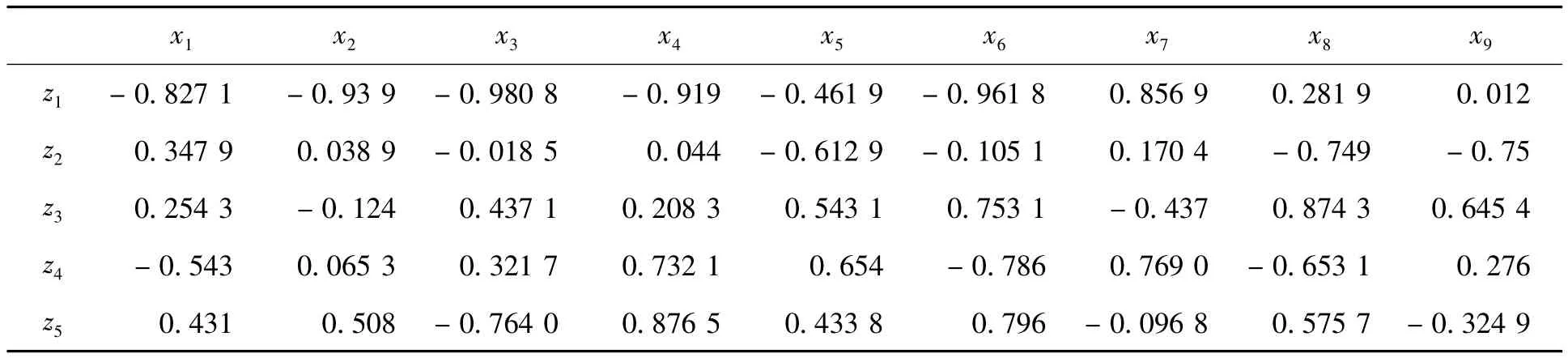
表2 正交旋转后的主因子载荷矩阵(红葡萄酒)
取得前五个主成分,各理化指标因子的二维载荷主平面数据表(见表2).依次分析五种主成分,得出红葡萄酒载荷较大的理化指标因子为:单宁,总酚,酒总黄酮,DPPH半抑制剂,色泽L*.分别令其为因变量x9,x10,x11,x12,x13.
2.2.3 分析酿酒红葡萄与红葡萄酒的理化指标之间的联系
分析酿酒红葡萄与红葡萄酒的理化指标之间的联系,要对每一个理化指标因子进行分析,显然这是不可行的.那么,我们首先分别用主成分分析法分析出酿酒红葡萄与红葡萄酒载荷较大的理化指标.另外从化学角度分析一下红葡萄酒的某项理化指标跟葡萄的某项理化指标显著相关的理化指标,求出红葡萄与红葡萄酒相应的理化指标之间的相关系数.从而减少了需要比较的因子数.结果如表3所示.
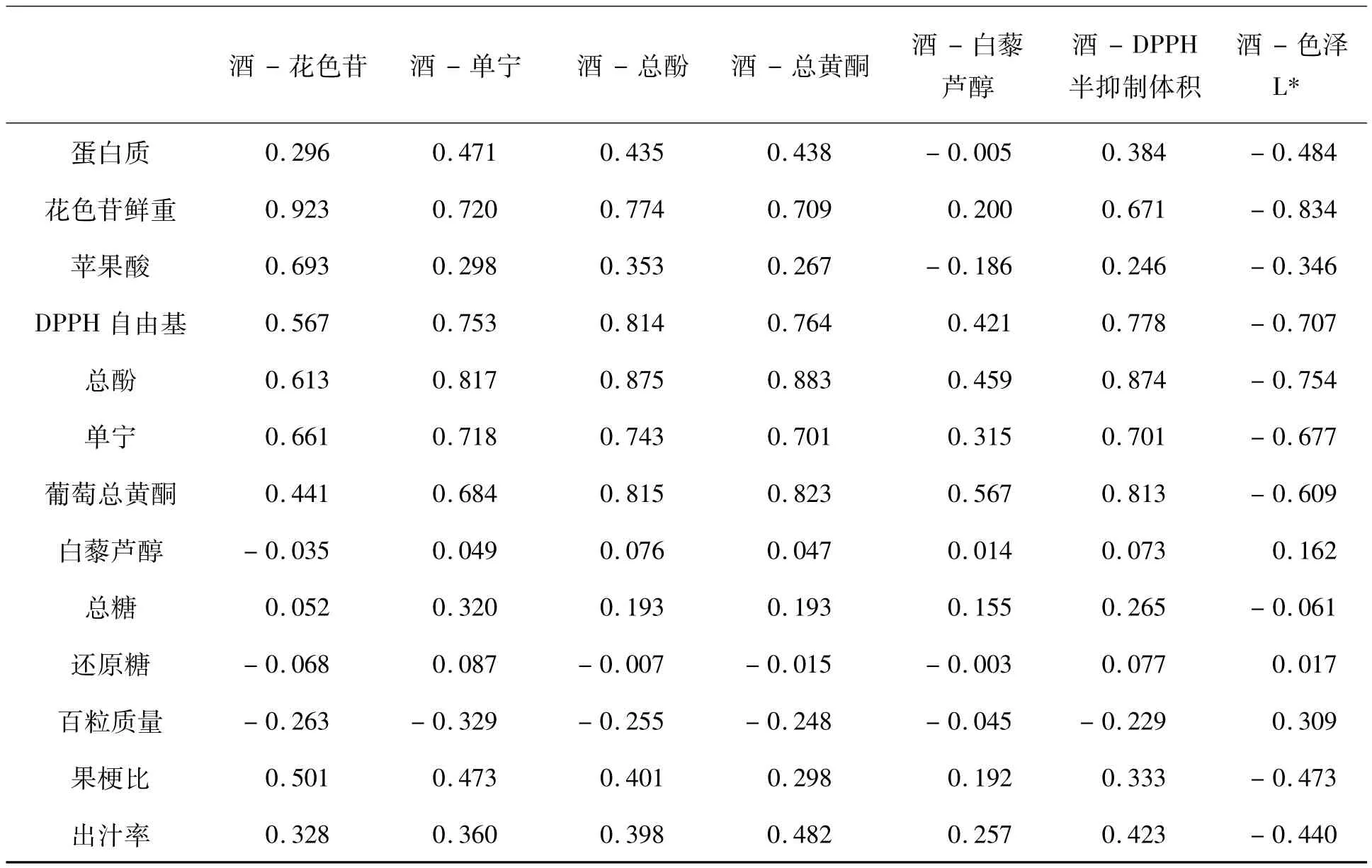
表3 红葡萄与红葡萄酒的理化指标之间的相关系数
我们规定两者的相关系数绝对值大于0.6时,认为两者的相关性显著.
2.2.4 定量分析酿酒红葡萄和红葡萄酒的理化指标对红葡萄酒质量的影响
上面我们用主成分分析法得到酿酒红葡萄与红葡萄酒的所有载荷较大的理化指标因子,以它们为自变量,把红葡萄酒的质量看作因变量,运用matlab软件用多元线性回归的方法得到自变量与因变量的函数表达式,从而定量的分析酿酒红葡萄和红葡萄酒的理化指标与红葡萄酒质量的确切关系.
用y表示红葡萄酒质量,运用matlab进行多元线性回归后得到的数学表达式为:

2.2.5 残差检验
为了避免在实际问题中,由于观察人员的粗心或偶然因素的干扰造成数据的不可靠,为此我们做出红葡萄酒品种数据的残差图,以此来分析多元线性回归模型的可行性.结果如图1所示.
由图1很容易看出,在27类数据中,除第26类数据外,其余数据的残差离零点都较近,并且它们残差的置信区间都包含了零点,由此看来多元线性回归能较好的符合原始数据,而第26类数据可视为异常.并进一步论证了用酿酒红葡萄和红葡萄酒的理化指标评价红葡萄酒质量的可行性,证明了多元线性回归模型的可靠性.
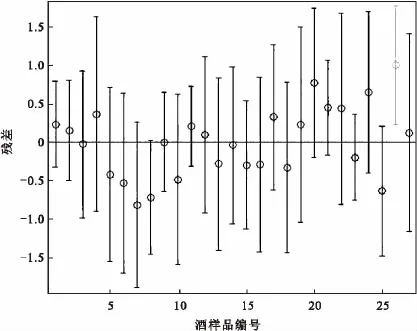
图1 红葡萄酒品种数据的残差图
3 总结及拓展
3.1 模型的总结分析
本文主要利用主成分分析,多元线性回归分析及残差检验等统计方法研究了酿酒红葡萄和红葡萄酒的理化指标之间的联系以及酿酒红葡萄和红葡萄酒的理化指标与红葡萄酒质量的关系等问题,获得了酿酒红葡萄和红葡萄酒的理化指标与红葡萄酒质量的方程.多元线性回归方程的方案,使得研究变得简单.但是模型在处理具体问题时难免存在着一些缺点,例如,对酿酒红葡萄与红葡萄酒的理化指标之间的联系只是做了定性的分析.
3.2 模型拓展分析
本文是对红葡萄酒质量评估模型的探究.当今社会食品安全已经成为我们最为关心的问题,并且在安全的基础上人们希望追求更高的品质.该红葡萄酒的质量评估模型,具有很大的延伸意义.一方面,我们可以用这种方法对酒品质量进行评估;另一方面,也给酿酒厂家在选材方面提供了可靠的参考.
[1] 王文静.感官评价在红葡萄酒研究中的应用[J].酿酒,2007,34(4):57-59.
[2] [美]FRANK R,GIORDAN O.A first course in mathematicalmodeling[M].Fourth Edition.Cengage Learning,2009.
[3] 何晓群.多元统计分析[M].北京:中国人大学出版社,2008.
[4] 杨桂元,黄已立.数学建模[M].合肥:中国科学技术大学出版社,2009.
[5] 刘卫国.MATLAB程序设计与应用[M].北京:高等教育出版社,2006.
[6] 姜启源.数学建模[M].2版.北京:高等教育出版社,2008.
[责任编辑 王新奇]
A Probe into W ine Quality Assessment M odel
KANGWei,SHENG Xiao-yan
(College of Information Engineering,Fuyang Teachers College,Fuyang 236041,China)
Adopting themethods of principal component analysis and multiple linear regression analysis,we have obtained functional relationship between wine quality and physicochemical indexes of grapes and grape wine.Residual test has proven the feasibility ofmulti-linear regression analysis.By combining the physicochemical indexes and organoleptic evaluation,we have constructed a new red wine quality assessmentmodel,which is supposed to be an improved one.
principal component analysis;correlation analysis;multiple linear regression analysis;residual test
1008-5564(2015)01-0027-05
O212.4
A
2014-09-12
国家自然科学基金天元基金(11226140);安徽省自然科学研究项目(KJ2013Z267);阜阳师范学院自然科学研究项目(2013FSKJ09);阜阳师范学院教学改革研究项目(2013JYXM48)
康 卫(1985—),男,安徽亳州人,阜阳师范学院信息工程学院助教,博士研究生,主要从事数学建模,控制理论研究.

