基于辫群的签名方案研究

魄 云， 朱双宁， 张兴凯， 王冠男

（1空军电子技术研究所， 北京 100195；296610 部队， 北京 102208 ）

基于辫群的签名方案研究

魄 云1， 朱双宁1， 张兴凯2， 王冠男1

（1空军电子技术研究所， 北京 100195；296610 部队， 北京 102208 ）

辫群是构造抗量子攻击密码方案的新平台。 本文对一个基于辫群上求根问题的签名方案进行分析，指出该方案是不安全的，得到签名的任何人都能计算出签名人的私钥;利用共扼搜索问题的难解性来隐藏用户的密钥信息，构造出新的签名方案，分析表明该方案是可证明安全的。

签名;辫群;共扼搜索问题;求根问题;随机预言模型

0 引言

量子计算[1-2］的快速发展使得安全性假设为整数分解和离散对数难解性的公钥密码体制面临严重威胁。为了抵抗已知量子算法的攻击，大量学者开始设计非基于数论的、基于非交换代数的公钥密码体制。 1947年，Artin[3］首次提出辫群这一代数结构，辫指数大于 2 的辫群具有复杂的非交换结构，为构造抗量子攻击密码体制提供了新的平台。 2000年，Ko 等[4］提出了第一个辫群上的公钥密码体制。 此后，众多学者相继提出了辫群上的密钥交换协议[5-6］、认 证 协 议[7-8］和签名方案[9-18］。 目前大多数基于辫群的签名方案安全性都是基于共扼类问题，属于共扼签名方案，不具有可证明安全性。

2010年，文献[19］首次基于辫群上的求根问题构造了具有可证明安全性的签名方案。本文对该方案的安全性进行分析，得出：任何人都能根据签名计算出签名人的私钥，因此该方案是不安全的。 本文对该方案进行改进，通过共扼作用实现对签名人私钥的保护，得到的签名方案仍然是可证明安全的。

本文第1节主要介绍辫群的相关概念及签名的安全模型;第2 节介绍文献[19］中的签名方案(简称为 WXBZ 方案） 并分析其安全性;第 3 节给出新的签名方案及其安全性分析;第 4 节总结全文。

1 相关知识

1.1 辫群及辫群上的难解问题

定义 1[4］辫群 Bn(n≥2 为 自然数）是由生成元 σ1，σ2，…，σn-1生成的有限表示的无限群。 其生成元满足：

σ1，σ2，…，σn-1称为辫群的生成子或 Artin 生成子，还称为初等辫子。 n称为辫指数，辫群中的元素称为一个 n辫子或辫元。B2是无限阶的循环群，本文不予考虑，当 n＞2 时 Bn是无限非交换群。
虽然辫群 Bn是无限非交换群，但它包含一些很大的子群，满足：来自不同子群的元素是交换的。 例如对于正整数 n1＜n，令LBn1，RBn-n1分 别 为 σ1，σ2，… ， σn1-1和 σn1+1，σn1+2， … ，σn-1生成的子群，称为 Bn的 n1-左子群和(n-n1）-右子 群。显然，对任意 α∈有 αβ = βα。 当 n1= ⌊ n/2」 时，将 Bn的 n1-左子群11和(n-n1）-右子群分别简称为左、右子群，记为 LBn和 RBn。 任意辫子 w∈Bn都可以唯一表示 成左规 范型 w= Δrα1… αq，q 称为 w的正规长度，r称为 w 的下确界，记作 inf(w），r+q 称为 w 的上确界，记作 sup(w）。

定义 2(共扼）对辫子 α，β∈Bn，如果存在辫子 s使得 β = s-1αs，则称 α，β 是共扼的，记作 α ～ β，s称为 α，β 的共扼子。

定义 3[4］共扼判断问题(Conjugacy Decision Problem）

问题实例：给定(α，β）∈Bn×Bn。

求解目标：判断 α～β 是否成立。

定义 4[4］共扼搜索问题(Conjugacy Search Problem）

问题实例：给定(α，β）∈Bn×Bn，满足 α～ β。

求解目标：找到一个 s∈Bn，使得 β =s-1αs。

定义 5[4］求根问题(Root Extraction Problem）

问题实例：给定整数 c(c＞1）及 β∈Bn，存在 α∈Bn使 β =αc。

求解目标：找到一个 γ∈Bn，使得 β = γc。

1.2 安全模型

对签名方案而言，适应性选择消息攻击下的存在性不可伪造是一种较强的安全性质。本文在随机预言模型下考虑适应性选择消息 攻 击 下 的 存 在 性 伪 造 (Existential Forgery under Adaptive Chosen Message Attack） ，通过挑战算法 C 和攻击算法 A 之间的游戏 Came来定义。 在该游戏中，C 和 A 进行如下交互：

1）C 生成系统参数及公钥 y，并发送给 A;

2）A 向 C 询问某些消息的杂凑值(C 模拟随机预言机 Oh）;

3）A 向 C 询问关于某些消息的签名(C 模拟签名预言机 Os）;

4）A 输出一个消息签名对(m，σ），满足条件：

(a）ver(m，σ，y）=1;

(b）m∉｛m＇｝，其中 ｛m＇｝ 表示出现在签名询问中的消息组成的集合。

如果某一多项式时间攻击算法 A能在时间 t内以不小于 ε的概率赢得游戏 Came，且满足：向 Oh提出询问的次数不超过 qh，向 Os询问的次数不超过 qs，称 A(t，ε，qh，qs） -攻击了签名方案。

定义 6[20］(不可伪造性） 如果不存在能(t，ε，qh，qs） -攻击某签名方案的多项式时间攻击算法，则称该签名方案对于适应性选择消息攻击下的存在性伪造是(t，ε，qh，qs） -不可伪造的。

2 WXBZ 方案分析

初始化：选择正整数 n、辫群 Bn、大素数 p 及 l。 令

Bn(l）= ｛ b∈Bn|0≤inf(b） ≤sup(b） ≤l｝

LBn(l）= ｛ b∈LBn|0≤inf(b） ≤sup(b） ≤l｝

RBn(l）= ｛ b∈RBn|0≤inf(b） ≤sup(b） ≤l｝

则 |Bn(l） |≤l(n!）l，Bn(l），LBn(l） 和 RBn(l） 都是有限集合。是抗碰撞的单向杂凑函数，其中p-1｝。

密钥生成：签名人随机选择 x∈LBn(l）作为私钥，计算 y=xp作为公钥。

签名：给定消息 m，签名人随机选择 t∈RBn(l），计算 T=tp，c =H(m||T），s=tx-c，

其中辫元 T在作为杂凑函数的输入时为二进制表示，关于消息 m 的签名为 σ =(c，s）。

签名验证：给定消息 m 的签名 σ=(c，s），验证者验证等式 c= H(m||spyc）是否成立，若成立，接受签名;否则，拒绝签名。

文献[21］有如下结论：对于给定的辫元 αβ，其中 α∈LBn，β∈RBn，存在一种能有效求解 α 和 β 的算法。 在上述签名方案中，s=tx-c，而 x∈LBn(l） ，t∈RBn(l） 。 因此，当签名 公布后，任何人可以求出(t，xc） 。 又因为(c，p） =1，当求出满足a1c+a2p=1 的(a1，a2） 后，任何人可计算 xa1cya2=xa1cxa2p=x， 即求出了签名人的私钥。

3 新的签名体制方案

3.1 签名方案

初始化及密钥生成过程同第3节。

签名：给定消息 m，签名人随机选择 t∈RBn(l）及 b∈Bn(l），计算 T=b-1tpb，Y=b-1yb，c=H(m||T），s=b-1tx-cb，关于消息 m 的签名为 σ=(c，s，Y）。

签名验证：给定消息 m 的签名 σ=(c，s，Y），验证者验证等式c=H(m||spYc）及 Y ～ y 是否成立，若都成立，接受签名;否则，拒绝签名。

3.2 方案分析

(1)完备性

由 x∈LBn，t∈RBn知 xt=tx，

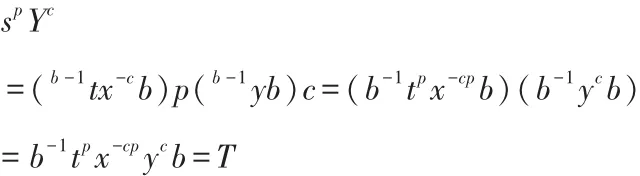
故 c=H(m||T）=H(m||spYc）。

由 Y=b-1yb 可知 Y～ y 成立，因此签名方案是完备的。

(2)不可伪造性

下面先给出证明不可伪造性所需的引理。

引理 1[22］对签名方案 REP-SS 考虑适应性选择消息攻击，设A是输入为公开参数的多项式时间算法，可以分别向随机预言机、签名预言机询问 qh和 qs次。 如果 A 能在时间 tA内，以概率 ε≥qsqh/N+2q2s/N+7qh/(p-1）成功地产生关于消息 m 的有效签名σ=(c，s，Y），且未向签名预言机询问过 m 的签名，则通过该算法可以在时间 t＇≤84480qhtA/(ε-qsqh/N-2q2s/N）内得到关于消息 m的两个有效签名 σ =(c，s，Y）和 σ＇=(c＇，s＇，Y） 满 足 c≠c＇，其中 N =|LBn(l） |· |Bn(l） |。

定理1在随机预言模型下，如果存在一个多项式时间攻击算法 A 能(tA，ε，qh，qs） -攻击该签名方案，其中 ε≥qsqh/N+2q2s/N+ 7qh/(p-1），则存在一个多项式时间挑战算法 C，能通过调用算法A 在时间 t＇≤84480qhtA/( ε-qsqh/N-2q2s/N）内解辫群上求根问题的一个实例，其中 N=|LBn(l） |· |Bn(l） |。

证明在求解过程中，C 必须对算法 A可询问的随机预言机和签名预言机进行模拟，模拟过程中分别为各预言机建立一个询问、回答相对应的关系列表 Lh和 Ls。 在与 A 交互之前，C 令 Lh= Φ，Ls=Φ。

当 A 向随机预言机 H 提出询问 m||T 时，C 执行：

1）检查询问 m||T 是否已经存在于列表 Lh中，若是，则返回对应的值;否则执行下一步;

2）随机选择 c∈｛1，…，p-1｝返回给 A 作为回答;

3）将该次询问及回答(m||T，c）添加到关系列表 Lh中，即令Lh=LhU｛(m||T，c）｝。

对签名预言机的模拟：当 A 向签名预言机询问关于消息 mi(1≤i≤qs） 的签名时，C 按如下方式执行：

1）随机选择 ci∈｛1，…，p-1｝;

2）随机选择 ti∈Bn(l），验证是否成立，若不是，重新选择 ti;否则，继续下一步;

3）随机选择 bi∈Bn(l），计算

4） 检查 mi||Ti是否已经存在于关系列表 Lh中，若 mi||Ti存在于 Lh中，且对应回答为 ci，则输出签名 σi=(ci，si，Yi），并令 Ls=LsU｛ (mi，σi） ｝;若 mi||Ti存在于 Lh中，而对应回答不为 ci，返回至第(1）步重新选择 ci并继续执行;若 mi||Ti不存在于 Lh中，则将 ci作为与询问 mi||Ti对应的回答保存到关系列表 Lh中，即令 Lh=LhU｛(mi||Ti，ci）｝ ，并输出签名 σi=(ci，si，Yi） ，令 Ls=LsU｛(mi，σi）｝ 。

由引理 1 可知，若 A 在时间 tA内以概率 ε≥qsqh/N+2q2s/N+ 7qh/(p-1）成功伪造出消息 m 的签名 σ =(c，s，Y），则 C 可以在时间内得到两个有效的签名 σ = (c，s，Y）和 σ＇=(c＇，s＇，Y）满足

不妨设 Y=b-1yb，即有

由签名方案中的 t∈RBn(l） ，x∈LBn(l）及 s=b-1tx-cb 可知，对于两个有效签名 σ =(c，s，Y） 和 σ＇=(c＇，s＇，Y），s 和 s＇由同样的 t和不同的 c得到，则应有

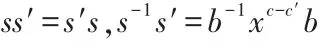
由 c，c＇∈｛1，…，p-1｝，c≠c＇可知 0＜ |c-c＇|＜p。 p 是素数，则存在整数 a1，a2满足 a1(c-c＇）+a2p=1。 C 通过计算

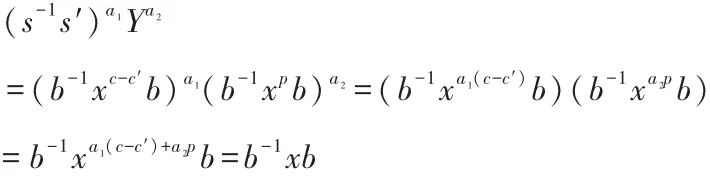
可得到 b-1xb，即 C 求得了 Y 的 p 次根。

由定理1可知，该方案在适应性选择消息攻击下是存在性不可伪造的。

4 结语

辫群作为构造密码协议的新平台，一经提出就成为研究热点。本文对基于辫群上求根问题的签名方案进行了分析和改进，构造了一个可证明安全的签名方案。 与共扼盲签名体制相比，新的签名体制在计算效率和签名长度上都有优势。

[1］Shor PW.Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J］ .SIAM Journal on Computing， 1997， 26(5） ： 1484-1509.

[2 ］Kitaev A.Quantum measurements and the abelian stabilizer problem[EB/OL］.http： //arxiv.org/quant-ph/9511026.

[3］Artin E.Theory of braids[J］ .Annals of Mathematics Studies，1947， 48(2）： 101-126.

[4］Ko KH， Lee SJ， Cheon JH， et al.New public key cryptosystem using braid groups[C］ //Proceedings of Crypto-2000， Lecture Notes in Computer Science， Benlin： Springer-Verlag， 2000，1880： 166-183.

[5］Anshel I， Anshel M， Fisher B， et al.New key agreement protocol in braid group cryptography[C］ //Topics in Cryptology-CT-RSA 2001， Lectures Notes in Computer Science， Benlin：Springer-Verlag， 2001， 2020： 1-15.

[6］Cha JC， Ko KH， Lee SJ， et al.An efficient implementation of braid groups[C］ //In： Advances in Cryptology： Proceedings of ASIACRYPT 2001， Lecture Notes in Computer Science，Benlin： Springer-Verlag， 2001， 2248： 144-156.

[7 ］Sibert H， Dehornoy P， Girault M.Entity authentication schemes using braid word reduction[EB/OL］ .http： //eprint. iacr.Org/2002/187.

[8］Lal S and Chaturvedi A.Authentication schemes using braid groups[EB/OL］.http： //arXiv.org/cs.CR/0507066.

[9］Ko KH， Choi DH， Cho MS， et al.New signature scheme using conjugacy problem[EB/OL ］ .http： //eprint.iacr.org/ 2002/168.

[10］丁勇， 田海博， 王育民.一种改进的基于辫群的签名体制[J］.西安电子科技大学学报， 2006， 33(1）： 50-52.

[11］Thomas T， Lal AK.Group signature scheme using braid groups[EB/OL］ .http： //arXiv.org/cs.CR/0602063.

[12］Verma GK.Blind signature schemes over braid groups[EB/ OL］.http： //eprint.iacr.org/2008/027.

[13］Verma GK.A proxy signature scheme over braid groups[EB/ OL］.http： //eprint.iacr.org/2008/160.

[14］Zhang LL， Zeng JW.Proxy signature based on braid group [J］ .Journal of Mathematical Study， 2008， 41(1） ： 56-64.

[15］Lal S and Verma V.Some proxy signature and designated verifier signature schemes over braid groups[EB/OL］ .http： // arXiv.org/cs.CR/09043422.

[16 ］Verma GK.A proxy blind signature scheme over braid groups[J ］ .International Journal of Network Security，2009， 9(3） ： 214-217.

[17］魄云， 张兴凯， 熊国华等.辫群上代理签名体制的分析与设计[J］.计算机应用研究， 2011， 28(9）： 3522-3524.

[18］魄云， 熊国华， 张兴凯等.辫群上的强盲签名体制[J］.中国科学院研究生院学报， 2011， 28(6）： 826-831.

[19］魄云， 熊国华， 鲍皖苏等.辫群上新的签名体制[J］.电子与信息学报， 2010， 32(12）： 2930-2934.

[20］Pointcheval D and Stern J.Security Arguments for Digital Signatures and Blind Signatures[J］ .Journal of Cryptology，2000， 13(3）： 361-396.

[21］Tsaban B.On an Authentication Scheme Based on the Root Problem in the Braid Group[EB/OL］ .http： //arxiv.org/abs/ math.GR/0509059.

[22］魄云.辫群上的数字签名研究[D］.郑州：信息工程大学，2011.

《通信技术》征稿启示

《通信技术》 是国内创办时间长、影响大的 IT 专业媒体，由中国电子科技集团公司主管、中国电子科技集团公司第三十研究所主办，主要报道信源处理、传输、业务与系统、网络、移动通信、信息安全等方面的先进技术、理论研究成果和最新动态。

自 1967年创刊以来，《 通信技术》一直以促进民族通信事业的发展为已任，搭建了一个联系编读交流、展示通信技术发展的良好平台。 在强化品质、不断创新的基础上，《通信技术》将以崭新的面貌出现在您的面前——更新颖的内容、更美观的版面、更精美的印刷。为扩大学术交流的渠道，本刊特向社会征集优秀稿件。

热诚欢迎通信技术领域从事科学、教学、技术开发、维护管理等方面的专家、学者、在校师生和相关技术人员踊跃投稿。

征稿内容：信源处理;传输;业务和系统;网络;移动通信; 通信保密

在线投稿：www.txjszz.com/jwk-xxaq/ht-login.jsp

电 话：028-85169918/85151528 传 真：028-85151528

《通信技术》编辑部

二O一四年一月一日

Signature Scheme based on Braid Groups

WEI Yun1， ZHU Shuang-ning1， ZHANG Xing-kai2， WANG Guan-nan1
(1AF 1Institute of Electronic Technology，Beijing 100195，China;2PLA 2Unit 96610， Beijing 102208， China）

Braid group is a new platform for constructing quantum attack-resistant cryptographic scheme.A signature scheme based on of root-extraction problem of braid groups is analyzed ， and its security vunerability is pointed out that the private key of the signer can be figured out once the signature is known.For this reason， the intractability of conjugacy search problem is used to hide the user's private key and build new signature scheme.Analysis indicates that this proposed scheme is provable secure.

signature;braid group;conjugacy search problem;root-extraction problem;random oracle model

TP309

A

1009-8054(2015)03-0085-04

魄 云(1982—），女，博士，工程师，主要研究方向为公钥密码学;

朱双宁(1978—），男，硕士，工程师，主要研究方向为信息安全;

张兴凯(1981—），男，硕士，工程师，主要研究方向为信息安全;

王冠男(1981—），女，硕士，工程师，主要研究方向为计算机应用。■

2014-12-11